Article contents
Numerical and experimental investigation of oblique shock wave reflection off a water wedge
Published online by Cambridge University Press: 10 August 2017
Abstract
Shock wave interaction with solid wedges has been an area of much research in past decades, but so far very few results have been obtained for shock wave reflection off liquid wedges. In this study, numerical simulations are performed using the inviscid Euler equations and the stiffened gas equation of state to study the transition angles, reflection patterns and triple point trajectory angles of shock reflection off solid and water wedges. Experiments using an inclined shock tube are also performed and schlieren photography results are compared to simulations. Results show that the transition angles for the water wedge cases are within 5.3 % and 9.2 %, for simulations and experiments respectively, compared to results obtained with the theoretical detachment criterion for solid surfaces. Triple point trajectory angles are measured and compared with analytic solutions, agreement within 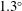 $1.3^{\circ }$ is shown for the water wedge cases. The transmitted wave in the water observed in the simulation is quantitatively studied, and two different scenarios are found. For low incident shock Mach numbers,
$1.3^{\circ }$ is shown for the water wedge cases. The transmitted wave in the water observed in the simulation is quantitatively studied, and two different scenarios are found. For low incident shock Mach numbers, 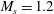 $M_{s}=1.2$ and 2, no shock wave is formed in the water but a precursor wave is induced ahead of the incident shock wave and passes the information from the water back into the air. For high incident shock Mach numbers,
$M_{s}=1.2$ and 2, no shock wave is formed in the water but a precursor wave is induced ahead of the incident shock wave and passes the information from the water back into the air. For high incident shock Mach numbers, 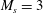 $M_{s}=3$ and 4, precursor waves no longer appear but instead a shock wave is formed in the water and attached to the Mach stem at every instant. The temperature field in the water is measured in the simulation. For strong incident shock waves, e.g.
$M_{s}=3$ and 4, precursor waves no longer appear but instead a shock wave is formed in the water and attached to the Mach stem at every instant. The temperature field in the water is measured in the simulation. For strong incident shock waves, e.g. 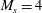 $M_{s}=4$ , the temperature increment in the water is up to 7.3 K.
$M_{s}=4$ , the temperature increment in the water is up to 7.3 K.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 17
- Cited by


