Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jahangir, Saad
Hogendoorn, Willian
and
Poelma, Christian
2018.
Dynamics of partial cavitation in an axisymmetric converging-diverging nozzle.
International Journal of Multiphase Flow,
Vol. 106,
Issue. ,
p.
34.
Wang, Chang-chang
Huang, Biao
Wang, Guo-yu
Duan, Zhong-ping
and
Ji, Bin
2018.
Numerical simulation of transient turbulent cavitating flows with special emphasis on shock wave dynamics considering the water/vapor compressibility.
Journal of Hydrodynamics,
Vol. 30,
Issue. 4,
p.
573.
Hosbach, Markus
Gitau, Stephen
Sander, Tobias
Leuteritz, Uwe
and
Pfitzner, Michael
2019.
Effect of taper, pressure and temperature on cavitation extent and dynamics in micro-channels.
Experimental Thermal and Fluid Science,
Vol. 108,
Issue. ,
p.
25.
Wu, Juliana
Ganesh, Harish
and
Ceccio, Steven
2019.
Multimodal partial cavity shedding on a two-dimensional hydrofoil and its relation to the presence of bubbly shocks.
Experiments in Fluids,
Vol. 60,
Issue. 4,
Long, Yun
Long, Xinping
Ji, Bin
and
Xing, Tao
2019.
Verification and validation of Large Eddy Simulation of attached cavitating flow around a Clark-Y hydrofoil.
International Journal of Multiphase Flow,
Vol. 115,
Issue. ,
p.
93.
Arabnejad, Mohammad Hossein
Amini, Ali
Farhat, Mohamed
and
Bensow, Rickard E.
2019.
Numerical and experimental investigation of shedding mechanisms from leading-edge cavitation.
International Journal of Multiphase Flow,
Vol. 119,
Issue. ,
p.
123.
Ye, Bingsheng
Wang, Yiwei
Huang, Chenguang
and
Huang, Jian
2019.
Numerical study of the pressure wave-induced shedding mechanism in the cavitating flow around an axisymmetric projectile via a compressible multiphase solver.
Ocean Engineering,
Vol. 187,
Issue. ,
p.
106179.
Zhang, Xingkai
Wang, Dong
Liao, Ruiquan
Zhao, Hui
and
Shi, Baocheng
2019.
Study of mechanical choked Venturi nozzles used for liquid flow controlling.
Flow Measurement and Instrumentation,
Vol. 65,
Issue. ,
p.
158.
Kadivar, Ebrahim
Timoshevskiy, Mikhail V.
Pervunin, Konstantin S.
and
Moctar, Ould el
2020.
Experimental and numerical study of the cavitation surge passive control around a semi-circular leading-edge flat plate.
Journal of Marine Science and Technology,
Vol. 25,
Issue. 4,
p.
1010.
Long, Yun
Long, Xinping
and
Ji, Bin
2020.
LES investigation of cavitating flows around a sphere with special emphasis on the cavitation–vortex interactions.
Acta Mechanica Sinica,
Vol. 36,
Issue. 6,
p.
1238.
Bai, Xiaorui
Cheng, Huaiyu
Ji, Bin
Long, Xinping
Qian, Zhongdong
and
Peng, Xiaoxing
2020.
Comparative Study of different vortex identification methods in a tip-leakage cavitating flow.
Ocean Engineering,
Vol. 207,
Issue. ,
p.
107373.
Asnaghi, Abolfazl
Svennberg, Urban
Gustafsson, Robert
and
Bensow, Rickard E.
2020.
Investigations of tip vortex mitigation by using roughness.
Physics of Fluids,
Vol. 32,
Issue. 6,
Trummler, Theresa
Schmidt, Steffen J.
and
Adams, Nikolaus A.
2020.
Investigation of condensation shocks and re-entrant jet dynamics in a cavitating nozzle flow by Large-Eddy Simulation.
International Journal of Multiphase Flow,
Vol. 125,
Issue. ,
p.
103215.
Wang, Changchang
Wang, Guoyu
and
Huang, Biao
2020.
Dynamics of unsteady compressible cavitating flows associated with the cavity shedding.
Ocean Engineering,
Vol. 209,
Issue. ,
p.
107025.
Qiu, Ning
Zhou, Wenjie
Che, Bangxiang
Wu, Dazhuan
Wang, Leqin
and
Zhu, Han
2020.
Effects of microvortex generators on cavitation erosion by changing periodic shedding into new structures.
Physics of Fluids,
Vol. 32,
Issue. 10,
Chen, Jian
Geng, Linlin
and
Escaler, Xavier
2020.
Numerical Investigation of the Cavitation Effects on the Vortex Shedding from a Hydrofoil with Blunt Trailing Edge.
Fluids,
Vol. 5,
Issue. 4,
p.
218.
Brunhart, Maxwell
Soteriou, Celia
Gavaises, Manolis
Karathanassis, Ioannis
Koukouvinis, Phoevos
Jahangir, Saad
and
Poelma, Christian
2020.
Investigation of cavitation and vapor shedding mechanisms in a Venturi nozzle.
Physics of Fluids,
Vol. 32,
Issue. 8,
Ganesh, Harish
Bhatt, Anubhav
Wu, Juliana
and
Ceccio, Steven
2020.
Effect of compressibility on bubbly cavitating flows.
Journal of Hydrodynamics,
Vol. 32,
Issue. 1,
p.
1.
Petkovšek, Martin
Hočevar, Marko
and
Dular, Matevž
2020.
Visualization and measurements of shock waves in cavitating flow.
Experimental Thermal and Fluid Science,
Vol. 119,
Issue. ,
p.
110215.
Brandao, Filipe L.
Bhatt, Mrugank
and
Mahesh, Krishnan
2020.
Numerical study of cavitation regimes in flow over a circular cylinder.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
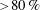 ${>}80\,\%$ for its spanwise average. Very good agreement is further obtained for the shedding Strouhal number, the cavity growth and collapse velocities, and for typical coherent flow structures. In accordance with the experiments, the simulations reproduce a condensation shock forming at the trailing part of the partial cavity. It is demonstrated that it satisfies locally Rankine–Hugoniot jump relations. Estimation of the shock propagation Mach number shows that the flow is supersonic. With a magnitude of only a few kPa, the pressure rise across the shock is much lower than for typical cavity collapse events. It is thus far too weak to cause cavitation erosion directly. However, by affecting the dynamics of the cavity, the flow aggressiveness can be significantly altered. Our results indicate that, in addition to classically observed re-entrant jets, condensation shocks feed an intrinsic instability mechanism of partial cavitation.
${>}80\,\%$ for its spanwise average. Very good agreement is further obtained for the shedding Strouhal number, the cavity growth and collapse velocities, and for typical coherent flow structures. In accordance with the experiments, the simulations reproduce a condensation shock forming at the trailing part of the partial cavity. It is demonstrated that it satisfies locally Rankine–Hugoniot jump relations. Estimation of the shock propagation Mach number shows that the flow is supersonic. With a magnitude of only a few kPa, the pressure rise across the shock is much lower than for typical cavity collapse events. It is thus far too weak to cause cavitation erosion directly. However, by affecting the dynamics of the cavity, the flow aggressiveness can be significantly altered. Our results indicate that, in addition to classically observed re-entrant jets, condensation shocks feed an intrinsic instability mechanism of partial cavitation.

