Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marchioli, Cristian
and
Soldati, Alfredo
2015.
Turbulent breakage of ductile aggregates.
Physical Review E,
Vol. 91,
Issue. 5,
Spandan, Vamsi
Lohse, Detlef
and
Verzicco, Roberto
2016.
Deformation and orientation statistics of neutrally buoyant sub-Kolmogorov ellipsoidal droplets in turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 809,
Issue. ,
p.
480.
Solsvik, Jannike
and
Jakobsen, Hugo A.
2016.
A review of the statistical turbulence theory required extending the population balance closure models to the entire spectrum of turbulence.
AIChE Journal,
Vol. 62,
Issue. 5,
p.
1795.
Saha, Debashish
Babler, Matthaus U.
Holzner, Markus
Soos, Miroslav
Lüthi, Beat
Liberzon, Alex
and
Kinzelbach, Wolfgang
2016.
Breakup of Finite-Size Colloidal Aggregates in Turbulent Flow Investigated by Three-Dimensional (3D) Particle Tracking Velocimetry.
Langmuir,
Vol. 32,
Issue. 1,
p.
55.
Njobuenwu, Derrick O.
and
Fairweather, Michael
2017.
Simulation of deterministic energy-balance particle agglomeration in turbulent liquid-solid flows.
Physics of Fluids,
Vol. 29,
Issue. 8,
Guseva, Ksenia
and
Feudel, Ulrike
2017.
Aggregation and fragmentation dynamics in random flows: From tracers to inertial aggregates.
Physical Review E,
Vol. 95,
Issue. 6,
Pozorski, Jacek
2017.
Particles in Wall-Bounded Turbulent Flows: Deposition, Re-Suspension and Agglomeration.
Vol. 571,
Issue. ,
p.
97.
Schutte, K. C. J.
Portela, L. M.
Twerda, A.
and
Henkes, R. A. W. M.
2018.
Formation and break-up of rigid agglomerates in turbulent channel and pipe flows.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
539.
Soldati, Alfredo
Zonta, Francesco
and
Lovecchio, Salvatore
2018.
Turbulence and Interactions.
Vol. 135,
Issue. ,
p.
55.
Liu, Peiyuan
and
Hrenya, Christine M.
2018.
Cluster-Induced Deagglomeration in Dilute Gravity-Driven Gas-Solid Flows of Cohesive Grains.
Physical Review Letters,
Vol. 121,
Issue. 23,
Johnson, Perry L.
and
Meneveau, Charles
2018.
Predicting viscous-range velocity gradient dynamics in large-eddy simulations of turbulence.
Journal of Fluid Mechanics,
Vol. 837,
Issue. ,
p.
80.
Njobuenwu, Derrick O.
and
Fairweather, Michael
2018.
Large eddy simulation of particle agglomeration with shear breakup in turbulent channel flow.
Physics of Fluids,
Vol. 30,
Issue. 6,
Gupta, A.
Clercx, H. J. H.
and
Toschi, F.
2018.
Computational study of radial particle migration and stresslet distributions in particle-laden turbulent pipe flow.
The European Physical Journal E,
Vol. 41,
Issue. 3,
Sadegh-Vaziri, Ramiar
Ludwig, Kristin
Sundmacher, Kai
and
Babler, Matthaus U.
2018.
Mechanisms behind overshoots in mean cluster size profiles in aggregation-breakup processes.
Journal of Colloid and Interface Science,
Vol. 528,
Issue. ,
p.
336.
Watteaux, R.
Sardina, G.
Brandt, L.
and
Iudicone, D.
2019.
On the time scales and structure of Lagrangian intermittency in homogeneous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 867,
Issue. ,
p.
438.
Penn, Roni
Maurer, Max
Michalec, François-Gaël
Scheidegger, Andreas
Zhou, Jiande
and
Holzner, Markus
2019.
Quantifying physical disintegration of faeces in sewers: Stochastic model and flow reactor experiments.
Water Research,
Vol. 152,
Issue. ,
p.
159.
Chen, Sheng
Li, Shuiqing
and
Marshall, Jeffrey S.
2019.
Exponential scaling in early-stage agglomeration of adhesive particles in turbulence.
Physical Review Fluids,
Vol. 4,
Issue. 2,
Wang, Guichao
Wan, Dongdong
Peng, Cheng
Liu, Ke
and
Wang, Lian-Ping
2019.
LBM study of aggregation of monosized spherical particles in homogeneous isotropic turbulence.
Chemical Engineering Science,
Vol. 201,
Issue. ,
p.
201.
Breuer, M.
and
Khalifa, A.
2019.
Revisiting and improving models for the breakup of compact dry powder agglomerates in turbulent flows within Eulerian–Lagrangian simulations.
Powder Technology,
Vol. 348,
Issue. ,
p.
105.
Breuer, M.
and
Khalifa, A.
2019.
Refinement of breakup models for compact powder agglomerates exposed to turbulent flows considering relevant time scales.
Computers & Fluids,
Vol. 194,
Issue. ,
p.
104315.
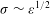 ${\it\sigma}\sim {\it\varepsilon}^{1/2}$ , with
${\it\sigma}\sim {\it\varepsilon}^{1/2}$ , with  ${\it\varepsilon}$ being the energy dissipation at the position of the aggregate, overcomes a given threshold
${\it\varepsilon}$ being the energy dissipation at the position of the aggregate, overcomes a given threshold 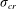 ${\it\sigma}_{cr}$ , which is characteristic for a given type of aggregate. Results show that the breakup rate decreases with increasing threshold. For small thresholds, it develops a scaling behaviour among the different flows. For high thresholds, the breakup rates show strong differences between the different flow configurations, highlighting the importance of non-universal mean-flow properties. To further assess the effects of flow inhomogeneity and turbulent fluctuations, the results are compared with those obtained in a smooth stochastic flow. Furthermore, we discuss the limitations and applicability of a set of independent proxies.
${\it\sigma}_{cr}$ , which is characteristic for a given type of aggregate. Results show that the breakup rate decreases with increasing threshold. For small thresholds, it develops a scaling behaviour among the different flows. For high thresholds, the breakup rates show strong differences between the different flow configurations, highlighting the importance of non-universal mean-flow properties. To further assess the effects of flow inhomogeneity and turbulent fluctuations, the results are compared with those obtained in a smooth stochastic flow. Furthermore, we discuss the limitations and applicability of a set of independent proxies.

