Article contents
Numerical study of viscous starting flow past wedges
Published online by Cambridge University Press: 19 July 2016
Abstract
This paper presents a numerical study of vortex formation in the impulsively started viscous flow past an infinite wedge, for wedge angles ranging from 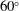 $60^{\circ }$ to
$60^{\circ }$ to 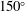 $150^{\circ }$ . The Navier–Stokes equations are solved in the vorticity-streamfunction formulation using a time-splitting scheme. The vorticity convection is computed using a semi-Lagrangian method. The vorticity diffusion is computed using an implicit finite difference scheme, after mapping the physical domain conformally onto a rectangle. The results show details of the vorticity evolution and associated streamline and streakline patterns. In particular, a hierarchical formation of recirculating regions corresponding to alternating signs of vorticity is revealed. The appearance times of these vorticity regions of alternate signs, as well as their dependence on the wedge angles, are investigated. The scaling behaviour of the vortex centre trajectory and vorticity is reported, and solutions are compared with those available from laboratory experiments and the inviscid similarity theory.
$150^{\circ }$ . The Navier–Stokes equations are solved in the vorticity-streamfunction formulation using a time-splitting scheme. The vorticity convection is computed using a semi-Lagrangian method. The vorticity diffusion is computed using an implicit finite difference scheme, after mapping the physical domain conformally onto a rectangle. The results show details of the vorticity evolution and associated streamline and streakline patterns. In particular, a hierarchical formation of recirculating regions corresponding to alternating signs of vorticity is revealed. The appearance times of these vorticity regions of alternate signs, as well as their dependence on the wedge angles, are investigated. The scaling behaviour of the vortex centre trajectory and vorticity is reported, and solutions are compared with those available from laboratory experiments and the inviscid similarity theory.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 4
- Cited by


