Article contents
On a suspension of nearly spherical colloidal particles under large-amplitude oscillatory shear flow
Published online by Cambridge University Press: 22 February 2016
Abstract
The dynamics of a dilute, monodisperse suspension of nearly spherical particles that undergo Brownian rotations in an oscillatory simple shear flow is quantified, as a paradigm for large-amplitude oscillatory shear (LAOS) rheology of complex fluids. We focus on the ‘strongly nonlinear’ regime of LAOS, defined by 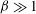 ${\it\beta}\gg 1$ and
${\it\beta}\gg 1$ and 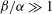 ${\it\beta}/{\it\alpha}\gg 1$ , where
${\it\beta}/{\it\alpha}\gg 1$ , where 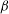 ${\it\beta}$ is a dimensionless shear rate (or Weissenberg number) and
${\it\beta}$ is a dimensionless shear rate (or Weissenberg number) and  ${\it\alpha}$ is a dimensionless oscillation frequency (or Deborah number). We derive an asymptotic solution for the long-time periodic orientation probability density function of the particles. Our analysis reveals that the orientation dynamics consists of ‘core’ regions of rapid oscillation (on the time scale of the inverse of the shear-rate amplitude), separated by comparatively short ‘turning’ regions of slow evolution when the imposed flow vanishes. Uniformly valid approximations to the shear stress and normal stress differences (NSDs) of the suspension are then constructed: the non-Newtonian contribution to the shear stress, first NSD and second NSD, decays as
${\it\alpha}$ is a dimensionless oscillation frequency (or Deborah number). We derive an asymptotic solution for the long-time periodic orientation probability density function of the particles. Our analysis reveals that the orientation dynamics consists of ‘core’ regions of rapid oscillation (on the time scale of the inverse of the shear-rate amplitude), separated by comparatively short ‘turning’ regions of slow evolution when the imposed flow vanishes. Uniformly valid approximations to the shear stress and normal stress differences (NSDs) of the suspension are then constructed: the non-Newtonian contribution to the shear stress, first NSD and second NSD, decays as  ${\it\beta}^{-3/2}$ ,
${\it\beta}^{-3/2}$ , 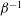 ${\it\beta}^{-1}$ and
${\it\beta}^{-1}$ and 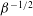 ${\it\beta}^{-1/2}$ , respectively, at large
${\it\beta}^{-1/2}$ , respectively, at large 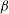 ${\it\beta}$ . These stress scalings originate from the orientation dynamics at the turning regions. Therefore, it is the occasions when the flow vanishes that dominate the rheology of this paradigmatic complex fluid under LAOS.
${\it\beta}$ . These stress scalings originate from the orientation dynamics at the turning regions. Therefore, it is the occasions when the flow vanishes that dominate the rheology of this paradigmatic complex fluid under LAOS.
Information
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 11
- Cited by


