1 Introduction
Thermal convection in fluids driven by spatial temperature variations has been investigated during the last decades in many theoretical and experimental studies (see e.g. Lappa Reference Lappa2009). The most studied example is Rayleigh–Bénard convection (RBC), where a fluid layer is heated from below and cooled from above. The standard theoretical description is based on the Oberbeck–Boussinesq equations (OBE), which couple the temperature and the velocity field. The main control parameter is the Rayleigh number
![]() $R$
, a dimensionless measure of the applied temperature gradient. Theoreticians have extensively analysed the OBE as a model system in order to explore a wide variety of different flow patterns and the transition to turbulence (see e.g. Verma Reference Verma2018). Besides
$R$
, a dimensionless measure of the applied temperature gradient. Theoreticians have extensively analysed the OBE as a model system in order to explore a wide variety of different flow patterns and the transition to turbulence (see e.g. Verma Reference Verma2018). Besides
![]() $R$
, the Prandtl number,
$R$
, the Prandtl number,
![]() $Pr$
, the ratio of the kinematical viscosity,
$Pr$
, the ratio of the kinematical viscosity,
![]() $\unicode[STIX]{x1D708}$
, and the thermal diffusivity,
$\unicode[STIX]{x1D708}$
, and the thermal diffusivity,
![]() $\unicode[STIX]{x1D705}$
, plays an important role for the solution manifold of the OBE. To simplify the calculations, one considers often fluid layers of large aspect ratio, i.e. with a height much smaller than the lateral extensions. The layer is then idealized as quasi-infinite and one switches with respect to the planar spatial coordinates into Fourier space. In this way the interpretation of the numerical results becomes much easier, apart from saving a lot of computer time.
$\unicode[STIX]{x1D705}$
, plays an important role for the solution manifold of the OBE. To simplify the calculations, one considers often fluid layers of large aspect ratio, i.e. with a height much smaller than the lateral extensions. The layer is then idealized as quasi-infinite and one switches with respect to the planar spatial coordinates into Fourier space. In this way the interpretation of the numerical results becomes much easier, apart from saving a lot of computer time.
For
![]() $R$
below the critical Rayleigh number,
$R$
below the critical Rayleigh number,
![]() $R_{c}$
, the system is in most cases, as also in the present paper, characterized by a uniform heat-conducting basic state. At
$R_{c}$
, the system is in most cases, as also in the present paper, characterized by a uniform heat-conducting basic state. At
![]() $R=R_{c}$
this state becomes linearly unstable and RBC sets in frequently in the form of a stationary two-dimensional (2-D) periodic array of counter-rotating convection rolls described by the critical wave vector
$R=R_{c}$
this state becomes linearly unstable and RBC sets in frequently in the form of a stationary two-dimensional (2-D) periodic array of counter-rotating convection rolls described by the critical wave vector
![]() $\boldsymbol{q}=\boldsymbol{q}_{c}$
. At a sufficiently large
$\boldsymbol{q}=\boldsymbol{q}_{c}$
. At a sufficiently large
![]() $R$
secondary and tertiary bifurcations of the roll patterns appear which lead to three-dimensional (3-D) patterns characterized by the impact of additional Fourier modes in wave vector space and possibly by a periodic time dependence as well.
$R$
secondary and tertiary bifurcations of the roll patterns appear which lead to three-dimensional (3-D) patterns characterized by the impact of additional Fourier modes in wave vector space and possibly by a periodic time dependence as well.
The construction of the corresponding stability diagrams in the
![]() $R-\boldsymbol{q}$
space for
$R-\boldsymbol{q}$
space for
![]() $R>R_{c}$
but not too large
$R>R_{c}$
but not too large
![]() $R$
(typically less than
$R$
(typically less than
![]() $5R_{c}$
), has been promoted since the sixties of the last century in particular by Busse and coworkers (see e.g. Busse Reference Busse and Peltier1989). Their general concept, which deploys its full power in Fourier space, has then been permanently extended and refined in many ways (for a general review, see Cross & Hohenberg (Reference Cross and Hohenberg1993)). It will be described in the following by the notion bifurcation approach, which still serves as the common starting point to explore new aspects in pattern-forming systems. In particular in gases with
$5R_{c}$
), has been promoted since the sixties of the last century in particular by Busse and coworkers (see e.g. Busse Reference Busse and Peltier1989). Their general concept, which deploys its full power in Fourier space, has then been permanently extended and refined in many ways (for a general review, see Cross & Hohenberg (Reference Cross and Hohenberg1993)). It will be described in the following by the notion bifurcation approach, which still serves as the common starting point to explore new aspects in pattern-forming systems. In particular in gases with
![]() $Pr\sim 1$
and not too large
$Pr\sim 1$
and not too large
![]() $R$
the bifurcation approach has led to a very convincing description of many experiments (for a recent review see, e.g. Bodenschatz, Pesch & Ahlers (Reference Bodenschatz, Pesch and Ahlers2000) and references therein). It is obvious that the bifurcation approach cannot work for turbulent convection at large
$R$
the bifurcation approach has led to a very convincing description of many experiments (for a recent review see, e.g. Bodenschatz, Pesch & Ahlers (Reference Bodenschatz, Pesch and Ahlers2000) and references therein). It is obvious that the bifurcation approach cannot work for turbulent convection at large
![]() $R\gtrsim 10^{3}R_{c}$
, which in addition is mostly explored in cylindrical geometries. Consequently we will typically not refer to the related papers; for a very recent and quite general discussion including many references we point to the monograph of Verma (Reference Verma2018).
$R\gtrsim 10^{3}R_{c}$
, which in addition is mostly explored in cylindrical geometries. Consequently we will typically not refer to the related papers; for a very recent and quite general discussion including many references we point to the monograph of Verma (Reference Verma2018).
In the present paper we investigate a variant of RBC, namely inclined layer convection (ILC), where the fluid layer is tilted by an angle
![]() $\unicode[STIX]{x1D6FE}$
with respect to the horizontal orientation. In contrast to the planar case (
$\unicode[STIX]{x1D6FE}$
with respect to the horizontal orientation. In contrast to the planar case (
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
) isotropy is broken by a shear flow, since already in the basic state the fluid flows downwards at the colder upper part of the fluid layer and upwards along the warmer lower one. Thus it is not surprising that ILC has attracted also theoretical studies for decades, mainly for medium and large
$\unicode[STIX]{x1D6FE}=0^{\circ }$
) isotropy is broken by a shear flow, since already in the basic state the fluid flows downwards at the colder upper part of the fluid layer and upwards along the warmer lower one. Thus it is not surprising that ILC has attracted also theoretical studies for decades, mainly for medium and large
![]() $Pr$
. In particular we refer to a recent paper for
$Pr$
. In particular we refer to a recent paper for
![]() $Pr\sim 1$
and references therein (Subramanian et al.
Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) for not too large
$Pr\sim 1$
and references therein (Subramanian et al.
Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) for not too large
![]() $R$
, where the bifurcation approach predicts already near
$R$
, where the bifurcation approach predicts already near
![]() $R_{c}$
as a function of
$R_{c}$
as a function of
![]() $\unicode[STIX]{x1D6FE}$
, a large variety of different 3-D pattern types in excellent agreement with the experiments.
$\unicode[STIX]{x1D6FE}$
, a large variety of different 3-D pattern types in excellent agreement with the experiments.
Motivated by recent papers on ILC with liquid metals, which are characterized by very small
![]() $Pr<0.1$
, in the turbulent regime with large
$Pr<0.1$
, in the turbulent regime with large
![]() $R\gtrsim 10^{6}$
(Shishkina & Horn Reference Shishkina and Horn2016; Teimurazov & Frick Reference Teimurazov and Frick2017) we found it attractive to perform a complementary study of this system using the bifurcation approach and direct numerical simulations (DNS) at small
$R\gtrsim 10^{6}$
(Shishkina & Horn Reference Shishkina and Horn2016; Teimurazov & Frick Reference Teimurazov and Frick2017) we found it attractive to perform a complementary study of this system using the bifurcation approach and direct numerical simulations (DNS) at small
![]() $R$
slightly above
$R$
slightly above
![]() $R_{c}$
. For definiteness we have restricted ourselves to mercury with
$R_{c}$
. For definiteness we have restricted ourselves to mercury with
![]() $Pr=0.025$
. First, we found oscillatory secondary instabilities of the basic rolls, well known already for
$Pr=0.025$
. First, we found oscillatory secondary instabilities of the basic rolls, well known already for
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
(see e.g. Rossby Reference Rossby1969), which lead to time-dependent oscillatory (OS) patterns in the form of waves along the roll axes. On the other hand, already even for small
$\unicode[STIX]{x1D6FE}=0^{\circ }$
(see e.g. Rossby Reference Rossby1969), which lead to time-dependent oscillatory (OS) patterns in the form of waves along the roll axes. On the other hand, already even for small
![]() $\unicode[STIX]{x1D6FE}$
competing stationary instabilities have been identified. They lead to specific, so-called subharmonic (SH), 3-D patterns, which are time independent. The detailed analysis of the competition between the OS and the SH patterns sets the frame of the present work.
$\unicode[STIX]{x1D6FE}$
competing stationary instabilities have been identified. They lead to specific, so-called subharmonic (SH), 3-D patterns, which are time independent. The detailed analysis of the competition between the OS and the SH patterns sets the frame of the present work.
The paper is organized as follows: after introducing the OBE for ILC in § 2, we sketch the linear instability of the basic state leading to transverse rolls. The critical Rayleigh number
![]() $R_{c}$
and the critical wavenumber
$R_{c}$
and the critical wavenumber
![]() $q_{c}$
are given as functions of
$q_{c}$
are given as functions of
![]() $\unicode[STIX]{x1D6FE}$
. Then Galerkin methods are applied to characterize the secondary instabilities of the transverse rolls as a function of
$\unicode[STIX]{x1D6FE}$
. Then Galerkin methods are applied to characterize the secondary instabilities of the transverse rolls as a function of
![]() $\unicode[STIX]{x1D6FE}$
. In the following section (§ 3) DNS of the OBE for different
$\unicode[STIX]{x1D6FE}$
. In the following section (§ 3) DNS of the OBE for different
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $R>R_{c}$
are presented, which confirm the Galerkin stability diagram. It is demonstrated that the arising 3-D patterns, either oscillatory or stationary, can be understood in terms of simple analytical expressions. In § 4 a number of complex patterns are discussed, which appear in particular near the various codimension-2 points with respect to
$R>R_{c}$
are presented, which confirm the Galerkin stability diagram. It is demonstrated that the arising 3-D patterns, either oscillatory or stationary, can be understood in terms of simple analytical expressions. In § 4 a number of complex patterns are discussed, which appear in particular near the various codimension-2 points with respect to
![]() $\unicode[STIX]{x1D6FE}$
, where the bifurcation switches from oscillatory to stationary. A short summary of the paper together with perspectives for future work can be found in the conclusions (§ 5). Finally, two appendices are devoted to the numerical methods used in this paper and in particular to a quite detailed discussion of the OS and SH patterns.
$\unicode[STIX]{x1D6FE}$
, where the bifurcation switches from oscillatory to stationary. A short summary of the paper together with perspectives for future work can be found in the conclusions (§ 5). Finally, two appendices are devoted to the numerical methods used in this paper and in particular to a quite detailed discussion of the OS and SH patterns.
2 Roll solutions and their stability
As sketched in figure 1 we consider in this paper ILC as function of the inclination angle
![]() $\unicode[STIX]{x1D6FE}$
(
$\unicode[STIX]{x1D6FE}$
(
![]() $0^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 90^{\circ }$
). The convection cell is cooled from above (at
$0^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 90^{\circ }$
). The convection cell is cooled from above (at
![]() $z=d/2$
) with the fixed temperature
$z=d/2$
) with the fixed temperature
![]() $T=T_{2}$
and heated from below (at
$T=T_{2}$
and heated from below (at
![]() $z=-d/2$
) with fixed
$z=-d/2$
) with fixed
![]() $T=T_{1}$
, where
$T=T_{1}$
, where
![]() $\unicode[STIX]{x0394}T=T_{1}-T_{2}>0$
. As already indicated before we concentrate on mercury as the working fluid, i.e. exclusively on
$\unicode[STIX]{x0394}T=T_{1}-T_{2}>0$
. As already indicated before we concentrate on mercury as the working fluid, i.e. exclusively on
![]() $Pr=0.025$
. In the following we discuss first the basic equations. Their linear analysis yields the primary instabilities of the basic state in the form of 2-D convection rolls with the wave vector
$Pr=0.025$
. In the following we discuss first the basic equations. Their linear analysis yields the primary instabilities of the basic state in the form of 2-D convection rolls with the wave vector
![]() $\boldsymbol{q}=\boldsymbol{q}_{c}$
at the critical Rayleigh number
$\boldsymbol{q}=\boldsymbol{q}_{c}$
at the critical Rayleigh number
![]() $R=R_{c}$
. For
$R=R_{c}$
. For
![]() $R>R_{c}$
the amplitudes of the rolls continuously grow until at a secondary instability, depending on
$R>R_{c}$
the amplitudes of the rolls continuously grow until at a secondary instability, depending on
![]() $\unicode[STIX]{x1D6FE}$
, different 3-D patterns bifurcate.
$\unicode[STIX]{x1D6FE}$
, different 3-D patterns bifurcate.
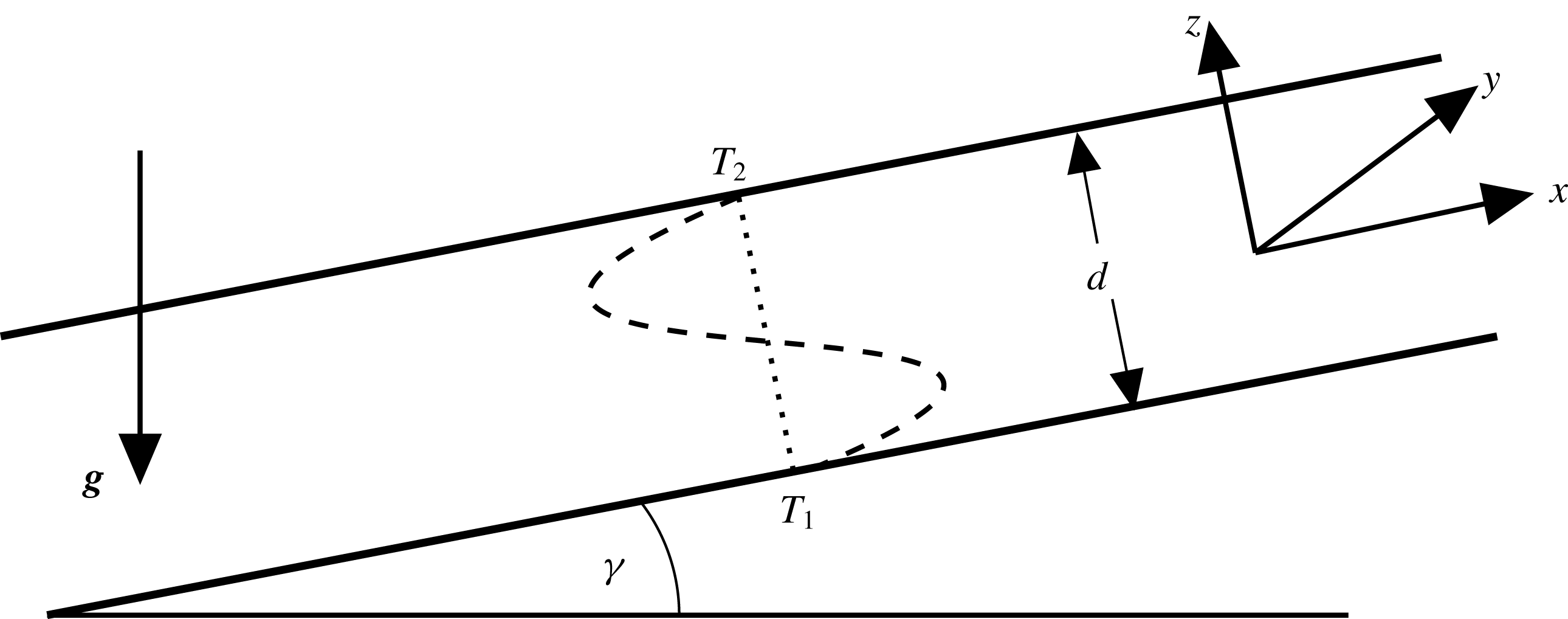
Figure 1. Fluid layer of thickness
![]() $d$
inclined with an angle
$d$
inclined with an angle
![]() $\unicode[STIX]{x1D6FE}$
, heated from below and cooled from above with temperature difference
$\unicode[STIX]{x1D6FE}$
, heated from below and cooled from above with temperature difference
![]() $\unicode[STIX]{x0394}T\equiv T_{1}-T_{2}>0$
. Driven by gravity
$\unicode[STIX]{x0394}T\equiv T_{1}-T_{2}>0$
. Driven by gravity
![]() $\boldsymbol{g}$
the cold fluid flows downwards near the top plate and the hot one flows upwards near the bottom plate leading to a cubic velocity profile across the fluid layer (see (2.2)).
$\boldsymbol{g}$
the cold fluid flows downwards near the top plate and the hot one flows upwards near the bottom plate leading to a cubic velocity profile across the fluid layer (see (2.2)).
2.1 Basic equations
The interaction of the temperature and velocity field in our system is described by the standard OBE for incompressible fluids. As usual, the OBE are non-dimensionalized using
![]() $d$
as the length scale and the vertical diffusion time
$d$
as the length scale and the vertical diffusion time
![]() $t_{v}=d^{2}/\unicode[STIX]{x1D705}$
as the time scale. The velocity
$t_{v}=d^{2}/\unicode[STIX]{x1D705}$
as the time scale. The velocity
![]() $\boldsymbol{u}$
is measured in units of
$\boldsymbol{u}$
is measured in units of
![]() $d/t_{v}$
, the pressure
$d/t_{v}$
, the pressure
![]() $p$
in units of
$p$
in units of
![]() $\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D708}d^{2})$
. Temperatures are measured in units of
$\unicode[STIX]{x1D705}/(\unicode[STIX]{x1D708}d^{2})$
. Temperatures are measured in units of
![]() $T_{s}=\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}/\unicode[STIX]{x1D6FC}gd^{3}$
with
$T_{s}=\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}/\unicode[STIX]{x1D6FC}gd^{3}$
with
![]() $\unicode[STIX]{x1D6FC}$
the thermal expansion coefficient. Using a Cartesian coordinate system aligned with the layer (see figure 1), the non-dimensional OBE read as follows:
$\unicode[STIX]{x1D6FC}$
the thermal expansion coefficient. Using a Cartesian coordinate system aligned with the layer (see figure 1), the non-dimensional OBE read as follows:
In line with previous theoretical investigations of ILC on the basis of the bifurcation approach in the literature (see in particular Clever & Busse (Reference Clever and Busse1977), Busse & Clever (Reference Busse and Clever1992)) we use periodic boundary conditions with respect to
![]() $x$
and
$x$
and
![]() $y$
. At the vertical boundaries
$y$
. At the vertical boundaries
![]() $z=\pm 1/2$
(in dimensionless units) the temperatures are kept fixed and the velocity is assumed to vanish (rigid boundary conditions). Equations (2.1) then admit primary (basic) solutions (denoted with subscript 0) of a linear temperature profile
$z=\pm 1/2$
(in dimensionless units) the temperatures are kept fixed and the velocity is assumed to vanish (rigid boundary conditions). Equations (2.1) then admit primary (basic) solutions (denoted with subscript 0) of a linear temperature profile
![]() $\tilde{T}_{0}(z)$
and cubic shear velocity profile
$\tilde{T}_{0}(z)$
and cubic shear velocity profile
![]() $\boldsymbol{U}_{0}(z)$
,
$\boldsymbol{U}_{0}(z)$
,
In the presence of convection
![]() $\tilde{T}_{0}$
is modified by
$\tilde{T}_{0}$
is modified by
![]() $\unicode[STIX]{x1D703}(x,y,z,t)$
and
$\unicode[STIX]{x1D703}(x,y,z,t)$
and
![]() $\boldsymbol{U}_{0}$
by
$\boldsymbol{U}_{0}$
by
![]() $\boldsymbol{v}$
as follows:
$\boldsymbol{v}$
as follows:
which fulfil the boundary conditions
![]() $\unicode[STIX]{x1D703}(z=\pm 1/2)=\boldsymbol{v}(z=\pm 1/2)=0$
.
$\unicode[STIX]{x1D703}(z=\pm 1/2)=\boldsymbol{v}(z=\pm 1/2)=0$
.
It is convenient to map the solenoidal velocity field
![]() $\boldsymbol{v}$
in (2.3b
) by the well-known poloidal–toroidal decomposition to two scalar velocity functions
$\boldsymbol{v}$
in (2.3b
) by the well-known poloidal–toroidal decomposition to two scalar velocity functions
![]() $f,\unicode[STIX]{x1D6F7}(\boldsymbol{x},z,t)$
and a correction
$f,\unicode[STIX]{x1D6F7}(\boldsymbol{x},z,t)$
and a correction
![]() $\boldsymbol{U}(z,t)=(U_{x},U_{y},0)$
of
$\boldsymbol{U}(z,t)=(U_{x},U_{y},0)$
of
![]() $\boldsymbol{U}_{0}(z)$
(2.2b
),
$\boldsymbol{U}_{0}(z)$
(2.2b
),
The equations for
![]() $f,\unicode[STIX]{x1D6F7}$
are obtained by inserting
$f,\unicode[STIX]{x1D6F7}$
are obtained by inserting
![]() $\boldsymbol{u}$
(2.3b
) with
$\boldsymbol{u}$
(2.3b
) with
![]() $\boldsymbol{v}$
(2.4) into (2.1b
) followed by the application of the operators
$\boldsymbol{v}$
(2.4) into (2.1b
) followed by the application of the operators
![]() $\unicode[STIX]{x1D74C},\boldsymbol{\unicode[STIX]{x1D702}}$
. The equation for
$\unicode[STIX]{x1D74C},\boldsymbol{\unicode[STIX]{x1D702}}$
. The equation for
![]() $\unicode[STIX]{x1D703}$
results from inserting the ansatz for
$\unicode[STIX]{x1D703}$
results from inserting the ansatz for
![]() $\tilde{T}$
(2.3a
) into (2.1a
). The explicit expressions for the linear equations are thus given as
$\tilde{T}$
(2.3a
) into (2.1a
). The explicit expressions for the linear equations are thus given as
For the following, a compact symbolic representation of the OBE (2.1) transcribed to
![]() $\unicode[STIX]{x1D703},f,\unicode[STIX]{x1D6F7},\boldsymbol{U}$
using (2.3) and (2.4) is convenient,
$\unicode[STIX]{x1D703},f,\unicode[STIX]{x1D6F7},\boldsymbol{U}$
using (2.3) and (2.4) is convenient,
with
![]() $\boldsymbol{x}=(x,y)$
and the symbolic vector
$\boldsymbol{x}=(x,y)$
and the symbolic vector
![]() $\widehat{\boldsymbol{V}}=[\unicode[STIX]{x1D703},f,\unicode[STIX]{x1D6F7}]^{\text{T}}$
. The linear operators
$\widehat{\boldsymbol{V}}=[\unicode[STIX]{x1D703},f,\unicode[STIX]{x1D6F7}]^{\text{T}}$
. The linear operators
![]() $\widehat{{\mathcal{C}}},\widehat{{\mathcal{L}}}$
are given in (2.5). The symbol
$\widehat{{\mathcal{C}}},\widehat{{\mathcal{L}}}$
are given in (2.5). The symbol
![]() $\widehat{\boldsymbol{N}}$
stands for the nonlinear terms which consist of quadratic forms in
$\widehat{\boldsymbol{N}}$
stands for the nonlinear terms which consist of quadratic forms in
![]() $\unicode[STIX]{x1D703},f,\unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D703},f,\unicode[STIX]{x1D6F7}$
and
![]() $\boldsymbol{U}$
and their spatial derivatives. The components of
$\boldsymbol{U}$
and their spatial derivatives. The components of
![]() $\widehat{\boldsymbol{N}}$
are given as
$\widehat{\boldsymbol{N}}$
are given as
The evolution equation for the secondary mean flow
![]() $\boldsymbol{U}(z,t)$
results from averaging the velocity equation (2.1b
) over the
$\boldsymbol{U}(z,t)$
results from averaging the velocity equation (2.1b
) over the
![]() $x{-}y$
plane, leading to
$x{-}y$
plane, leading to
where the overbar indicates the horizontal average. Note that (2.8) contains a special pressure term first proposed in Busse & Clever (Reference Busse and Clever2000) in a different context. The functions
![]() $P_{x}(t),P_{y}(t)$
have to be chosen to guarantee mass conservation, i.e.
$P_{x}(t),P_{y}(t)$
have to be chosen to guarantee mass conservation, i.e.
![]() $\int \text{d}z\boldsymbol{U}(z)=0$
; non-zero
$\int \text{d}z\boldsymbol{U}(z)=0$
; non-zero
![]() $P_{x,y}$
, however, appear only in the DNS of complex patterns in § 4.
$P_{x,y}$
, however, appear only in the DNS of complex patterns in § 4.
In general (2.6) is solved with respect to
![]() $x,y$
on a rectangle with the lateral extensions
$x,y$
on a rectangle with the lateral extensions
![]() $L_{x}$
,
$L_{x}$
,
![]() $L_{y}$
using periodic boundary condition, i.e.
$L_{y}$
using periodic boundary condition, i.e.
![]() $\widehat{\boldsymbol{V}}(x,y,z)=\widehat{\boldsymbol{V}}(x+L_{x},y+L_{y},z)$
holds. That is guaranteed by using the following discrete Fourier representation:
$\widehat{\boldsymbol{V}}(x,y,z)=\widehat{\boldsymbol{V}}(x+L_{x},y+L_{y},z)$
holds. That is guaranteed by using the following discrete Fourier representation:
where
![]() $\unicode[STIX]{x0394}q_{x}=2\unicode[STIX]{x03C0}/L_{x}$
,
$\unicode[STIX]{x0394}q_{x}=2\unicode[STIX]{x03C0}/L_{x}$
,
![]() $\unicode[STIX]{x0394}q_{y}=2\unicode[STIX]{x03C0}/L_{y}$
. Thus the simulations run in Fourier space on a 2-D grid of
$\unicode[STIX]{x0394}q_{y}=2\unicode[STIX]{x03C0}/L_{y}$
. Thus the simulations run in Fourier space on a 2-D grid of
![]() $N^{2}$
wave vectors. Since
$N^{2}$
wave vectors. Since
![]() $\boldsymbol{V}$
is real the condition
$\boldsymbol{V}$
is real the condition
![]() $\boldsymbol{V}(\boldsymbol{q},z,t)=\boldsymbol{V}(-\boldsymbol{q},z,t)^{\ast }$
has to be fulfilled.
$\boldsymbol{V}(\boldsymbol{q},z,t)=\boldsymbol{V}(-\boldsymbol{q},z,t)^{\ast }$
has to be fulfilled.
The boundary conditions like
![]() $\unicode[STIX]{x1D703}(z=\pm 1/2)=0$
are automatically satisfied by the use of truncated Galerkin expansions with respect to
$\unicode[STIX]{x1D703}(z=\pm 1/2)=0$
are automatically satisfied by the use of truncated Galerkin expansions with respect to
![]() $z$
. For example,
$z$
. For example,
![]() $\unicode[STIX]{x1D703}$
is represented by the ansatz
$\unicode[STIX]{x1D703}$
is represented by the ansatz
which is analogously used also for
![]() $\unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D6F7}$
and
![]() $\boldsymbol{U}(z,t)$
. The rigid boundary conditions for
$\boldsymbol{U}(z,t)$
. The rigid boundary conditions for
![]() $\boldsymbol{v}$
require that
$\boldsymbol{v}$
require that
![]() $f$
has to be expanded in terms of the Chandrasekhar functions
$f$
has to be expanded in terms of the Chandrasekhar functions
![]() $C_{m}(z)$
(Chandrasekhar Reference Chandrasekhar1961). Consequently our OBE are finally mapped to a system of ordinary differential equations in time for the Fourier coefficients of
$C_{m}(z)$
(Chandrasekhar Reference Chandrasekhar1961). Consequently our OBE are finally mapped to a system of ordinary differential equations in time for the Fourier coefficients of
![]() $\unicode[STIX]{x1D717}_{m}(\boldsymbol{x},t)$
and the corresponding ones for
$\unicode[STIX]{x1D717}_{m}(\boldsymbol{x},t)$
and the corresponding ones for
![]() $f,\unicode[STIX]{x1D6F7}$
and
$f,\unicode[STIX]{x1D6F7}$
and
![]() $\boldsymbol{U}$
. The Galerkin expansions with respect to the
$\boldsymbol{U}$
. The Galerkin expansions with respect to the
![]() $z$
-direction (see e.g. (2.10)) have been always truncated at
$z$
-direction (see e.g. (2.10)) have been always truncated at
![]() $M=8$
modes. In line with the Appendix of Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) we have tested by increasing
$M=8$
modes. In line with the Appendix of Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) we have tested by increasing
![]() $M$
that the numbers given in the present paper are afflicted with a relative error of less than 0.1 %.
$M$
that the numbers given in the present paper are afflicted with a relative error of less than 0.1 %.
2.2 Linear stability analysis of the basic state
The primary convection instability of the basic state corresponds to exponentially growing solutions in time of the linear equations (2.5). Thus, using the common convection roll ansatz
![]() $\widehat{\boldsymbol{V}}(\boldsymbol{x},z,t)=\text{e}^{\unicode[STIX]{x1D70E}t}\text{e}^{\text{i}\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{x}}\tilde{\boldsymbol{V}}(\boldsymbol{q},z,R)$
in (2.6) with
$\widehat{\boldsymbol{V}}(\boldsymbol{x},z,t)=\text{e}^{\unicode[STIX]{x1D70E}t}\text{e}^{\text{i}\boldsymbol{q}\boldsymbol{\cdot }\boldsymbol{x}}\tilde{\boldsymbol{V}}(\boldsymbol{q},z,R)$
in (2.6) with
![]() $\widehat{\boldsymbol{N}}=0$
, we arrive from (2.6) at the following linear eigenvalue problem for
$\widehat{\boldsymbol{N}}=0$
, we arrive from (2.6) at the following linear eigenvalue problem for
![]() $\unicode[STIX]{x1D70E}$
:
$\unicode[STIX]{x1D70E}$
:
where the operators
![]() ${\mathcal{C}},{\mathcal{L}}(\boldsymbol{q},\unicode[STIX]{x2202}_{z})$
, etc. in Fourier space derive from the corresponding ones in position space (see (2.5)) via the transformation
${\mathcal{C}},{\mathcal{L}}(\boldsymbol{q},\unicode[STIX]{x2202}_{z})$
, etc. in Fourier space derive from the corresponding ones in position space (see (2.5)) via the transformation
![]() $\unicode[STIX]{x2202}_{\boldsymbol{x}}\rightarrow \text{i}\boldsymbol{q}$
. As indicated before (see e.g. (2.10)) the
$\unicode[STIX]{x2202}_{\boldsymbol{x}}\rightarrow \text{i}\boldsymbol{q}$
. As indicated before (see e.g. (2.10)) the
![]() $z$
-dependence of
$z$
-dependence of
![]() $\tilde{\boldsymbol{V}}(\boldsymbol{q},z;R)$
is captured by Galerkin expansions with
$\tilde{\boldsymbol{V}}(\boldsymbol{q},z;R)$
is captured by Galerkin expansions with
![]() $M=8$
modes. It turns out that it is sufficient to confine the analysis to the
$M=8$
modes. It turns out that it is sufficient to confine the analysis to the
![]() $\unicode[STIX]{x1D703},f$
equations in (2.5). Thus, one arrives finally at an algebraic linear eigenvalue problem of dimension
$\unicode[STIX]{x1D703},f$
equations in (2.5). Thus, one arrives finally at an algebraic linear eigenvalue problem of dimension
![]() $2M$
in the Fourier–Galerkin space, which is analysed using a standard linear-algebra package, LAPACK. Let
$2M$
in the Fourier–Galerkin space, which is analysed using a standard linear-algebra package, LAPACK. Let
![]() $\unicode[STIX]{x1D70E}_{max}(R,Pr,\unicode[STIX]{x1D6FE},\boldsymbol{q})$
define the eigenvalue
$\unicode[STIX]{x1D70E}_{max}(R,Pr,\unicode[STIX]{x1D6FE},\boldsymbol{q})$
define the eigenvalue
![]() $\unicode[STIX]{x1D70E}$
with the largest real part in (2.11); then rolls become unstable when
$\unicode[STIX]{x1D70E}$
with the largest real part in (2.11); then rolls become unstable when
![]() $\unicode[STIX]{x1D70E}_{max}(R,Pr,\unicode[STIX]{x1D6FE},\boldsymbol{q})$
crosses zero. For each
$\unicode[STIX]{x1D70E}_{max}(R,Pr,\unicode[STIX]{x1D6FE},\boldsymbol{q})$
crosses zero. For each
![]() $\boldsymbol{q}$
we have to determine the smallest solution
$\boldsymbol{q}$
we have to determine the smallest solution
![]() $R=R_{0}(\boldsymbol{q})$
of
$R=R_{0}(\boldsymbol{q})$
of
![]() $Re[\unicode[STIX]{x1D70E}_{max}(\boldsymbol{q})]=0$
(the fixed parameters
$Re[\unicode[STIX]{x1D70E}_{max}(\boldsymbol{q})]=0$
(the fixed parameters
![]() $Pr,\unicode[STIX]{x1D6FE}$
are suppressed for the moment). The minimum of
$Pr,\unicode[STIX]{x1D6FE}$
are suppressed for the moment). The minimum of
![]() $R_{0}(\boldsymbol{q})$
with respect to
$R_{0}(\boldsymbol{q})$
with respect to
![]() $\boldsymbol{q}$
defines the critical wave vector
$\boldsymbol{q}$
defines the critical wave vector
![]() $\boldsymbol{q}_{c}$
and the critical Rayleigh number
$\boldsymbol{q}_{c}$
and the critical Rayleigh number
![]() $R_{c}=R_{0}(\boldsymbol{q}_{c})$
at which the basic state becomes unstable against convection rolls with wave vector
$R_{c}=R_{0}(\boldsymbol{q}_{c})$
at which the basic state becomes unstable against convection rolls with wave vector
![]() $\boldsymbol{q}_{c}$
. The bifurcation turns out to be always stationary since
$\boldsymbol{q}_{c}$
. The bifurcation turns out to be always stationary since
![]() $Im[\unicode[STIX]{x1D70E}_{max}(R_{c},\boldsymbol{q}_{c})]\equiv 0$
; otherwise one would speak of an oscillatory bifurcation.
$Im[\unicode[STIX]{x1D70E}_{max}(R_{c},\boldsymbol{q}_{c})]\equiv 0$
; otherwise one would speak of an oscillatory bifurcation.
It is convenient to parameterize the orientation of a wave vector
![]() $\boldsymbol{q}$
in the
$\boldsymbol{q}$
in the
![]() $x{-}y$
plane as
$x{-}y$
plane as
![]() $\boldsymbol{q}=\bar{q}(\unicode[STIX]{x1D713})(\cos \unicode[STIX]{x1D713},\sin \unicode[STIX]{x1D713})$
. Thus we obtain from
$\boldsymbol{q}=\bar{q}(\unicode[STIX]{x1D713})(\cos \unicode[STIX]{x1D713},\sin \unicode[STIX]{x1D713})$
. Thus we obtain from
![]() $Re[\unicode[STIX]{x1D70E}_{max}]=0$
the critical data
$Re[\unicode[STIX]{x1D70E}_{max}]=0$
the critical data
![]() $\bar{q}_{c}(\unicode[STIX]{x1D713}),\bar{R}_{c}(\unicode[STIX]{x1D713})$
, which depend on
$\bar{q}_{c}(\unicode[STIX]{x1D713}),\bar{R}_{c}(\unicode[STIX]{x1D713})$
, which depend on
![]() $\unicode[STIX]{x1D6FE}$
. At
$\unicode[STIX]{x1D6FE}$
. At
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
we deal with the standard isotropic RBC, where
$\unicode[STIX]{x1D6FE}=0^{\circ }$
we deal with the standard isotropic RBC, where
![]() $\bar{q}_{c}=q_{c0}=3.116$
and
$\bar{q}_{c}=q_{c0}=3.116$
and
![]() $\bar{R}_{c}=R_{c0}=1707.8$
depend neither on
$\bar{R}_{c}=R_{c0}=1707.8$
depend neither on
![]() $\unicode[STIX]{x1D713}$
nor on
$\unicode[STIX]{x1D713}$
nor on
![]() $Pr$
.
$Pr$
.

Figure 2. Linear instability of the ILC basic state for
![]() $Pr=0.025$
(see (2.2)) as a function of the inclination angle
$Pr=0.025$
(see (2.2)) as a function of the inclination angle
![]() $\unicode[STIX]{x1D6FE}$
with respect to rolls of wave vector
$\unicode[STIX]{x1D6FE}$
with respect to rolls of wave vector
![]() $\boldsymbol{q}=(q_{x},q_{y})=\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})(\cos \unicode[STIX]{x1D713},\sin \unicode[STIX]{x1D713})$
at
$\boldsymbol{q}=(q_{x},q_{y})=\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})(\cos \unicode[STIX]{x1D713},\sin \unicode[STIX]{x1D713})$
at
![]() $R=\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
. (a) Reduced critical Rayleigh number
$R=\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
. (a) Reduced critical Rayleigh number
![]() $\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})/R_{c0}$
(logarithmic scale) with
$\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})/R_{c0}$
(logarithmic scale) with
![]() $R_{c0}=1707.8$
. (b) Critical wavenumber
$R_{c0}=1707.8$
. (b) Critical wavenumber
![]() $\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
. The solid lines correspond to the transverse rolls, where
$\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
. The solid lines correspond to the transverse rolls, where
![]() $\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713}=0^{\circ })$
is minimal. For the other
$\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713}=0^{\circ })$
is minimal. For the other
![]() $\unicode[STIX]{x1D713}$
the following line styles are used: dotted for longitudinal rolls (
$\unicode[STIX]{x1D713}$
the following line styles are used: dotted for longitudinal rolls (
![]() $\unicode[STIX]{x1D713}=90^{\circ }$
), dashed for
$\unicode[STIX]{x1D713}=90^{\circ }$
), dashed for
![]() $\unicode[STIX]{x1D713}=75^{\circ }$
and dash-dotted for
$\unicode[STIX]{x1D713}=75^{\circ }$
and dash-dotted for
![]() $\unicode[STIX]{x1D713}=60^{\circ }$
.
$\unicode[STIX]{x1D713}=60^{\circ }$
.
In figure 2 one finds representative plots of
![]() $\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
and
$\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
and
![]() $\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
as function of
$\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713})$
as function of
![]() $\unicode[STIX]{x1D6FE}$
for different
$\unicode[STIX]{x1D6FE}$
for different
![]() $\unicode[STIX]{x1D713}$
at fixed
$\unicode[STIX]{x1D713}$
at fixed
![]() $Pr=0.025$
. One sees that the convection onset is realized by transverse rolls (
$Pr=0.025$
. One sees that the convection onset is realized by transverse rolls (
![]() $\unicode[STIX]{x1D713}=0^{\circ }$
) for all
$\unicode[STIX]{x1D713}=0^{\circ }$
) for all
![]() $\unicode[STIX]{x1D6FE}$
. This is in contrast to the case of medium
$\unicode[STIX]{x1D6FE}$
. This is in contrast to the case of medium
![]() $Pr$
. There exists a so-called codimension-2 point,
$Pr$
. There exists a so-called codimension-2 point,
![]() $\unicode[STIX]{x1D6FE}_{c2}$
, such that for
$\unicode[STIX]{x1D6FE}_{c2}$
, such that for
![]() $0^{\circ }<\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D6FE}_{c2}$
longitudinal rolls with
$0^{\circ }<\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D6FE}_{c2}$
longitudinal rolls with
![]() $\unicode[STIX]{x1D713}=90^{\circ }$
bifurcate at onset in contrast to transverse rolls (
$\unicode[STIX]{x1D713}=90^{\circ }$
bifurcate at onset in contrast to transverse rolls (
![]() $\unicode[STIX]{x1D713}=0^{\circ }$
) for
$\unicode[STIX]{x1D713}=0^{\circ }$
) for
![]() $\unicode[STIX]{x1D6FE}>\unicode[STIX]{x1D6FE}_{c2}$
. With decreasing Prandtl number
$\unicode[STIX]{x1D6FE}>\unicode[STIX]{x1D6FE}_{c2}$
. With decreasing Prandtl number
![]() $\unicode[STIX]{x1D6FE}_{c2}$
moves continuously downwards to zero until for
$\unicode[STIX]{x1D6FE}_{c2}$
moves continuously downwards to zero until for
![]() $Pr<0.264$
indeed only transverse rolls bifurcate at onset for
$Pr<0.264$
indeed only transverse rolls bifurcate at onset for
![]() $0^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$
(for a detailed discussion, see appendix C in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016)). It is further evident, that
$0^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$
(for a detailed discussion, see appendix C in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016)). It is further evident, that
![]() $R_{c}(\unicode[STIX]{x1D6FE})=\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713}=0^{\circ })$
decreases strongly with
$R_{c}(\unicode[STIX]{x1D6FE})=\bar{R}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713}=0^{\circ })$
decreases strongly with
![]() $\unicode[STIX]{x1D6FE}$
. This applies also to the critical wavenumber
$\unicode[STIX]{x1D6FE}$
. This applies also to the critical wavenumber
![]() $q_{c}(\unicode[STIX]{x1D6FE})=\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713}=0^{\circ })$
, although the decay is much weaker.
$q_{c}(\unicode[STIX]{x1D6FE})=\bar{q}_{c}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D713}=0^{\circ })$
, although the decay is much weaker.
To measure directly the relative distance of
![]() $R$
from
$R$
from
![]() $R_{c}$
we use in the following two definitions of a reduced control parameters, either
$R_{c}$
we use in the following two definitions of a reduced control parameters, either
![]() $\unicode[STIX]{x1D716}$
or
$\unicode[STIX]{x1D716}$
or
![]() $\unicode[STIX]{x1D716}_{0}$
, which are defined as
$\unicode[STIX]{x1D716}_{0}$
, which are defined as
Selected numerical values of
![]() $R_{c}$
and
$R_{c}$
and
![]() $q_{c}$
as functions of
$q_{c}$
as functions of
![]() $\unicode[STIX]{x1D6FE}$
, which correspond to the bold lower curves in figure 2, are listed in table 1. When gradually increasing
$\unicode[STIX]{x1D6FE}$
, which correspond to the bold lower curves in figure 2, are listed in table 1. When gradually increasing
![]() $R$
beyond
$R$
beyond
![]() $R_{c}(\unicode[STIX]{x1D6FE})$
finite-amplitude transverse roll patterns with wavenumber
$R_{c}(\unicode[STIX]{x1D6FE})$
finite-amplitude transverse roll patterns with wavenumber
![]() $q_{c}(\unicode[STIX]{x1D6FE})$
develop. Their stability analysis will be discussed in the following subsection.
$q_{c}(\unicode[STIX]{x1D6FE})$
develop. Their stability analysis will be discussed in the following subsection.
Table 1. Critical Rayleigh number
![]() $R_{c}(\unicode[STIX]{x1D6FE})$
and critical wavenumber
$R_{c}(\unicode[STIX]{x1D6FE})$
and critical wavenumber
![]() $q_{c}(\unicode[STIX]{x1D6FE})$
of transverse rolls together with
$q_{c}(\unicode[STIX]{x1D6FE})$
of transverse rolls together with
![]() $\unicode[STIX]{x1D716}_{0}=(R_{c}(\unicode[STIX]{x1D6FE})-R_{c0})/R_{c0}$
(2.12) for increasing
$\unicode[STIX]{x1D716}_{0}=(R_{c}(\unicode[STIX]{x1D6FE})-R_{c0})/R_{c0}$
(2.12) for increasing
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.

2.3 Secondary instabilities of transverse rolls
The finite-amplitude stationary transverse rolls which develop with wave vector
![]() $\boldsymbol{q}_{c}(\unicode[STIX]{x1D6FE})=(q_{c}(\unicode[STIX]{x1D6FE}),0)$
for
$\boldsymbol{q}_{c}(\unicode[STIX]{x1D6FE})=(q_{c}(\unicode[STIX]{x1D6FE}),0)$
for
![]() $R>R_{c}(\unicode[STIX]{x1D6FE})$
(see table 1) are represented as a special case of (2.9) as follows:
$R>R_{c}(\unicode[STIX]{x1D6FE})$
(see table 1) are represented as a special case of (2.9) as follows:
where a cutoff
![]() $N_{r}=10$
was found to be sufficient in the present context. With respect to
$N_{r}=10$
was found to be sufficient in the present context. With respect to
![]() $z$
, we introduce again a Galerkin expansion (see (2.10)) of the
$z$
, we introduce again a Galerkin expansion (see (2.10)) of the
![]() $(N_{r}+1)$
Fourier coefficients
$(N_{r}+1)$
Fourier coefficients
![]() $\boldsymbol{V}_{r}(kq_{c},z)$
. Thus we arrive at
$\boldsymbol{V}_{r}(kq_{c},z)$
. Thus we arrive at
![]() $(3M)N_{r}$
coupled nonlinear algebraic equations for the expansion coefficients in the resulting Fourier–Galerkin representation. Furthermore, the Galerkin expansion of the mean flow
$(3M)N_{r}$
coupled nonlinear algebraic equations for the expansion coefficients in the resulting Fourier–Galerkin representation. Furthermore, the Galerkin expansion of the mean flow
![]() $\boldsymbol{U}$
using sine functions leads to
$\boldsymbol{U}$
using sine functions leads to
![]() $2M$
additional equations. The whole system is then solved by Newton–Raphson methods. Non-trivial solutions exist only for
$2M$
additional equations. The whole system is then solved by Newton–Raphson methods. Non-trivial solutions exist only for
![]() $R>R_{c}(\boldsymbol{q})$
. Thus the bifurcation to transverse rolls is continuous (supercritical). To examine the linear stability of a transverse roll solution we linearize our general equations about
$R>R_{c}(\boldsymbol{q})$
. Thus the bifurcation to transverse rolls is continuous (supercritical). To examine the linear stability of a transverse roll solution we linearize our general equations about
![]() $\widehat{\boldsymbol{V}}_{r}(x,z)$
with respect to an infinitesimal perturbation
$\widehat{\boldsymbol{V}}_{r}(x,z)$
with respect to an infinitesimal perturbation
![]() $\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{V}}_{r}$
in the form of the standard Floquet ansatz
$\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{V}}_{r}$
in the form of the standard Floquet ansatz
Thus, we arrive at a linear eigenvalue problem for the eigenvalues
![]() $\unicode[STIX]{x1D6F4}(\boldsymbol{s},q_{c},R)$
at fixed
$\unicode[STIX]{x1D6F4}(\boldsymbol{s},q_{c},R)$
at fixed
![]() $R$
; the
$R$
; the
![]() $\unicode[STIX]{x1D6FE}$
-dependence will be typically suppressed in the following. The eigenvalue
$\unicode[STIX]{x1D6FE}$
-dependence will be typically suppressed in the following. The eigenvalue
![]() $\unicode[STIX]{x1D6F4}$
with the largest real part,
$\unicode[STIX]{x1D6F4}$
with the largest real part,
![]() $\unicode[STIX]{x1D6F4}_{0}(\boldsymbol{s},q_{c},R)$
, determines the growth rate of the perturbation
$\unicode[STIX]{x1D6F4}_{0}(\boldsymbol{s},q_{c},R)$
, determines the growth rate of the perturbation
![]() $\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{V}}_{r}$
in (2.14). The condition
$\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{V}}_{r}$
in (2.14). The condition
![]() $Re[\unicode[STIX]{x1D6F4}_{0}(\boldsymbol{s},q_{c},R)]=0$
indicates thus a secondary instability of the transverse rolls with wavenumber
$Re[\unicode[STIX]{x1D6F4}_{0}(\boldsymbol{s},q_{c},R)]=0$
indicates thus a secondary instability of the transverse rolls with wavenumber
![]() $q_{c}$
at
$q_{c}$
at
![]() $R=R_{0}(\boldsymbol{s},q_{c})$
. The minimum of
$R=R_{0}(\boldsymbol{s},q_{c})$
. The minimum of
![]() $R_{0}(\boldsymbol{s},q_{c})$
with respect to
$R_{0}(\boldsymbol{s},q_{c})$
with respect to
![]() $\boldsymbol{s}$
gives the Floquet vector
$\boldsymbol{s}$
gives the Floquet vector
![]() $\boldsymbol{s}_{in}(q_{c})$
of the most effective perturbation
$\boldsymbol{s}_{in}(q_{c})$
of the most effective perturbation
![]() $\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{V}}_{r}(\boldsymbol{x},z,t)$
driving the instability of the transverse rolls at
$\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{V}}_{r}(\boldsymbol{x},z,t)$
driving the instability of the transverse rolls at
![]() $R_{in}(q_{c})=R_{0}(\boldsymbol{s}_{in},q_{c})$
, where the index in points to secondary instability. The frequency at onset is determined by
$R_{in}(q_{c})=R_{0}(\boldsymbol{s}_{in},q_{c})$
, where the index in points to secondary instability. The frequency at onset is determined by
![]() $\unicode[STIX]{x1D714}_{in}=\text{Im}[\unicode[STIX]{x1D6F4}_{0}(\boldsymbol{s}_{in},q_{c},R_{in})]$
. For
$\unicode[STIX]{x1D714}_{in}=\text{Im}[\unicode[STIX]{x1D6F4}_{0}(\boldsymbol{s}_{in},q_{c},R_{in})]$
. For
![]() $|\unicode[STIX]{x1D714}_{in}|>0$
the secondary instability is oscillatory, otherwise stationary. The corresponding Fourier coefficient
$|\unicode[STIX]{x1D714}_{in}|>0$
the secondary instability is oscillatory, otherwise stationary. The corresponding Fourier coefficient
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{V}_{r}(kq_{c},z)$
in (2.14) takes its maximum for a value
$\unicode[STIX]{x1D6FF}\boldsymbol{V}_{r}(kq_{c},z)$
in (2.14) takes its maximum for a value
![]() $k=k_{max}$
with
$k=k_{max}$
with
![]() $|k_{max}|\leqslant 1$
. The most effective destabilizing modes are thus characterized by the wave vectors
$|k_{max}|\leqslant 1$
. The most effective destabilizing modes are thus characterized by the wave vectors
![]() $\boldsymbol{q}_{in}=(k_{max}\,q_{c},0)+\boldsymbol{s}_{in}$
. In the present system we find a twofold degeneracy of the eigenvalues
$\boldsymbol{q}_{in}=(k_{max}\,q_{c},0)+\boldsymbol{s}_{in}$
. In the present system we find a twofold degeneracy of the eigenvalues
![]() $\unicode[STIX]{x1D70E}_{0}(\boldsymbol{s}_{in},q_{c},R)$
, since they take the same values for
$\unicode[STIX]{x1D70E}_{0}(\boldsymbol{s}_{in},q_{c},R)$
, since they take the same values for
![]() $\boldsymbol{s}=(s_{x},\pm s_{y}^{in})$
. Depending on
$\boldsymbol{s}=(s_{x},\pm s_{y}^{in})$
. Depending on
![]() $\unicode[STIX]{x1D6FE}$
we find either oscillatory or stationary secondary instabilities. For the first one, with
$\unicode[STIX]{x1D6FE}$
we find either oscillatory or stationary secondary instabilities. For the first one, with
![]() $k_{max}=1$
, the dominant Fourier coefficients in (2.14) belong to the wave vectors
$k_{max}=1$
, the dominant Fourier coefficients in (2.14) belong to the wave vectors
![]() $\boldsymbol{q}_{2,3}=(q_{c},\pm s_{y}^{\mathit{OS}})$
, while for the second one with
$\boldsymbol{q}_{2,3}=(q_{c},\pm s_{y}^{\mathit{OS}})$
, while for the second one with
![]() $k_{max}=0$
the dominant modes belong to
$k_{max}=0$
the dominant modes belong to
![]() $\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y}^{SH})$
. In figure 3 we show the whole secondary-bifurcation diagram in the
$\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y}^{SH})$
. In figure 3 we show the whole secondary-bifurcation diagram in the
![]() $\unicode[STIX]{x1D6FE}{-}\unicode[STIX]{x1D716}$
plane for
$\unicode[STIX]{x1D6FE}{-}\unicode[STIX]{x1D716}$
plane for
![]() $Pr=0.025$
. The well-known OS instability at
$Pr=0.025$
. The well-known OS instability at
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
remains dominant up to the first codimension-2 point
$\unicode[STIX]{x1D6FE}=0^{\circ }$
remains dominant up to the first codimension-2 point
![]() $\unicode[STIX]{x1D6FE}_{1}=1.023^{\circ }$
. Then the stationary SH instability takes over in the interval
$\unicode[STIX]{x1D6FE}_{1}=1.023^{\circ }$
. Then the stationary SH instability takes over in the interval
![]() $\unicode[STIX]{x1D6FE}_{1}<\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D6FE}_{2}=2.183^{\circ }$
with the second codimension-2 point
$\unicode[STIX]{x1D6FE}_{1}<\unicode[STIX]{x1D6FE}<\unicode[STIX]{x1D6FE}_{2}=2.183^{\circ }$
with the second codimension-2 point
![]() $\unicode[STIX]{x1D6FE}_{2}$
. Up to the third codimension-2 point
$\unicode[STIX]{x1D6FE}_{2}$
. Up to the third codimension-2 point
![]() $\unicode[STIX]{x1D6FE}_{3}=6.169^{\circ }$
again the OS instability dominates, which is then finally replaced again by the subharmonic one for
$\unicode[STIX]{x1D6FE}_{3}=6.169^{\circ }$
again the OS instability dominates, which is then finally replaced again by the subharmonic one for
![]() $\unicode[STIX]{x1D6FE}_{3}<\unicode[STIX]{x1D6FE}<90^{\circ }$
. The detailed data for the two instabilities are contained in table 2 for a representative set of inclination angles
$\unicode[STIX]{x1D6FE}_{3}<\unicode[STIX]{x1D6FE}<90^{\circ }$
. The detailed data for the two instabilities are contained in table 2 for a representative set of inclination angles
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.
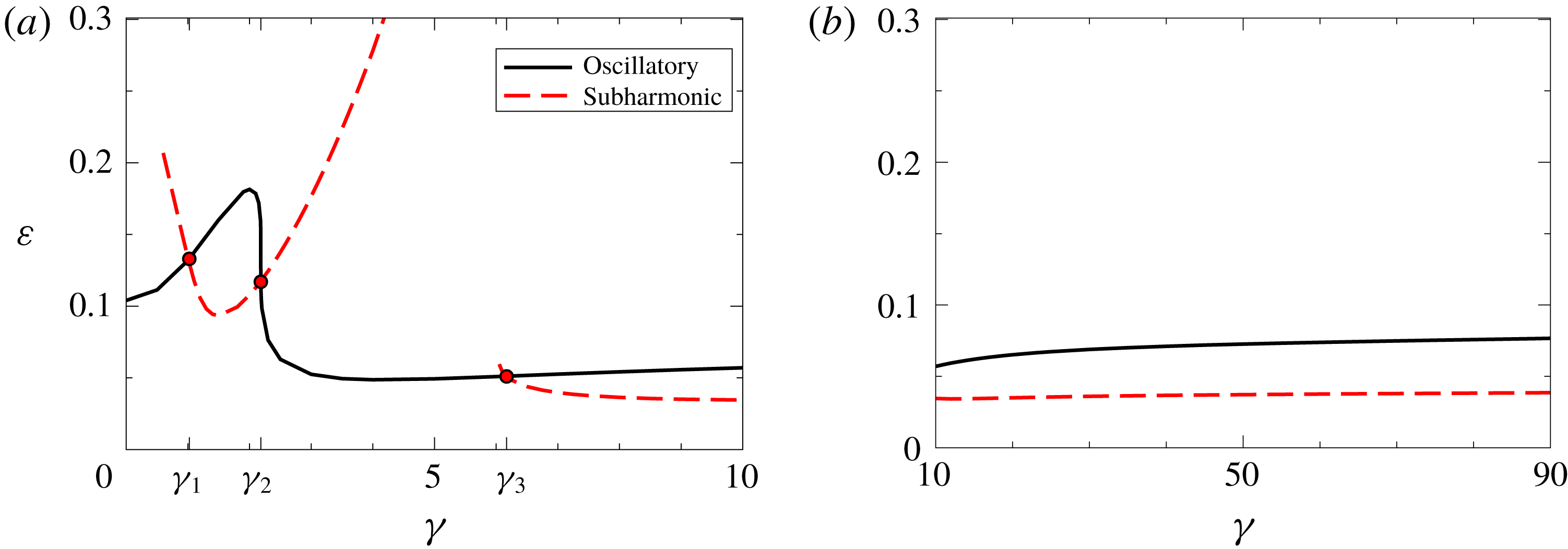
Figure 3. Stability diagram of transverse rolls for
![]() $Pr=0.025$
with
$Pr=0.025$
with
![]() $0^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 10^{\circ }$
(a) and
$0^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 10^{\circ }$
(a) and
![]() $10^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 90^{\circ }$
(b). The basic state in (2.2), stable for
$10^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 90^{\circ }$
(b). The basic state in (2.2), stable for
![]() $\unicode[STIX]{x1D716}<0$
(2.12), becomes unstable against the transverse rolls for
$\unicode[STIX]{x1D716}<0$
(2.12), becomes unstable against the transverse rolls for
![]() $\unicode[STIX]{x1D716}>0$
. These are stable below the lowest of the two lines, which determine either the OS instability at
$\unicode[STIX]{x1D716}>0$
. These are stable below the lowest of the two lines, which determine either the OS instability at
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{\mathit{OS}}$
(solid line) or the SH instability at
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{\mathit{OS}}$
(solid line) or the SH instability at
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{SH}$
(dashed). The three crossing points of the two curves define the codimension-2 points
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{SH}$
(dashed). The three crossing points of the two curves define the codimension-2 points
![]() $\unicode[STIX]{x1D6FE}_{1,2,3}$
.
$\unicode[STIX]{x1D6FE}_{1,2,3}$
.
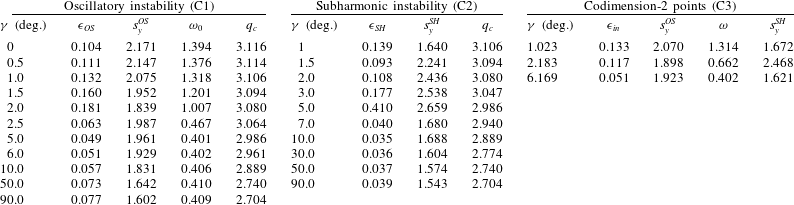
Table 2. Secondary instabilities of transverse rolls with wavenumber
![]() $q_{c}(\unicode[STIX]{x1D6FE})$
at
$q_{c}(\unicode[STIX]{x1D6FE})$
at
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{in}$
with Floquet vector
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{in}$
with Floquet vector
![]() $\boldsymbol{s}_{in}=(s_{x}^{in},s_{y}^{in})$
for selected values of the inclination angle
$\boldsymbol{s}_{in}=(s_{x}^{in},s_{y}^{in})$
for selected values of the inclination angle
![]() $\unicode[STIX]{x1D6FE}$
(see § 2.3). C1: OS instability at
$\unicode[STIX]{x1D6FE}$
(see § 2.3). C1: OS instability at
![]() $\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{\mathit{OS}}$
with
$\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{\mathit{OS}}$
with
![]() $\boldsymbol{s}_{in}=(0,s_{y}^{\mathit{OS}})$
and frequency
$\boldsymbol{s}_{in}=(0,s_{y}^{\mathit{OS}})$
and frequency
![]() $\unicode[STIX]{x1D714}_{0}$
. C2: SH instability at
$\unicode[STIX]{x1D714}_{0}$
. C2: SH instability at
![]() $\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{SH}$
with
$\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{SH}$
with
![]() $\boldsymbol{s}_{in}=(q_{c}/2,s_{y}^{SH})$
. C3: codimension-2 data (OS/SH) for
$\boldsymbol{s}_{in}=(q_{c}/2,s_{y}^{SH})$
. C3: codimension-2 data (OS/SH) for
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{i}$
, (
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{i}$
, (
![]() $i=1,2,3$
) at
$i=1,2,3$
) at
![]() $\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{\mathit{OS}}=\unicode[STIX]{x1D716}_{SH}$
with
$\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{\mathit{OS}}=\unicode[STIX]{x1D716}_{SH}$
with
![]() $s_{y}^{\mathit{OS}},\unicode[STIX]{x1D714}_{0}$
and
$s_{y}^{\mathit{OS}},\unicode[STIX]{x1D714}_{0}$
and
![]() $s_{y}^{SH}$
. As always in this paper,
$s_{y}^{SH}$
. As always in this paper,
![]() $\boldsymbol{s}_{in}$
is given in units of
$\boldsymbol{s}_{in}$
is given in units of
![]() $1/d$
and
$1/d$
and
![]() $\unicode[STIX]{x1D714}$
in units of
$\unicode[STIX]{x1D714}$
in units of
![]() $1/t_{v}$
.
$1/t_{v}$
.
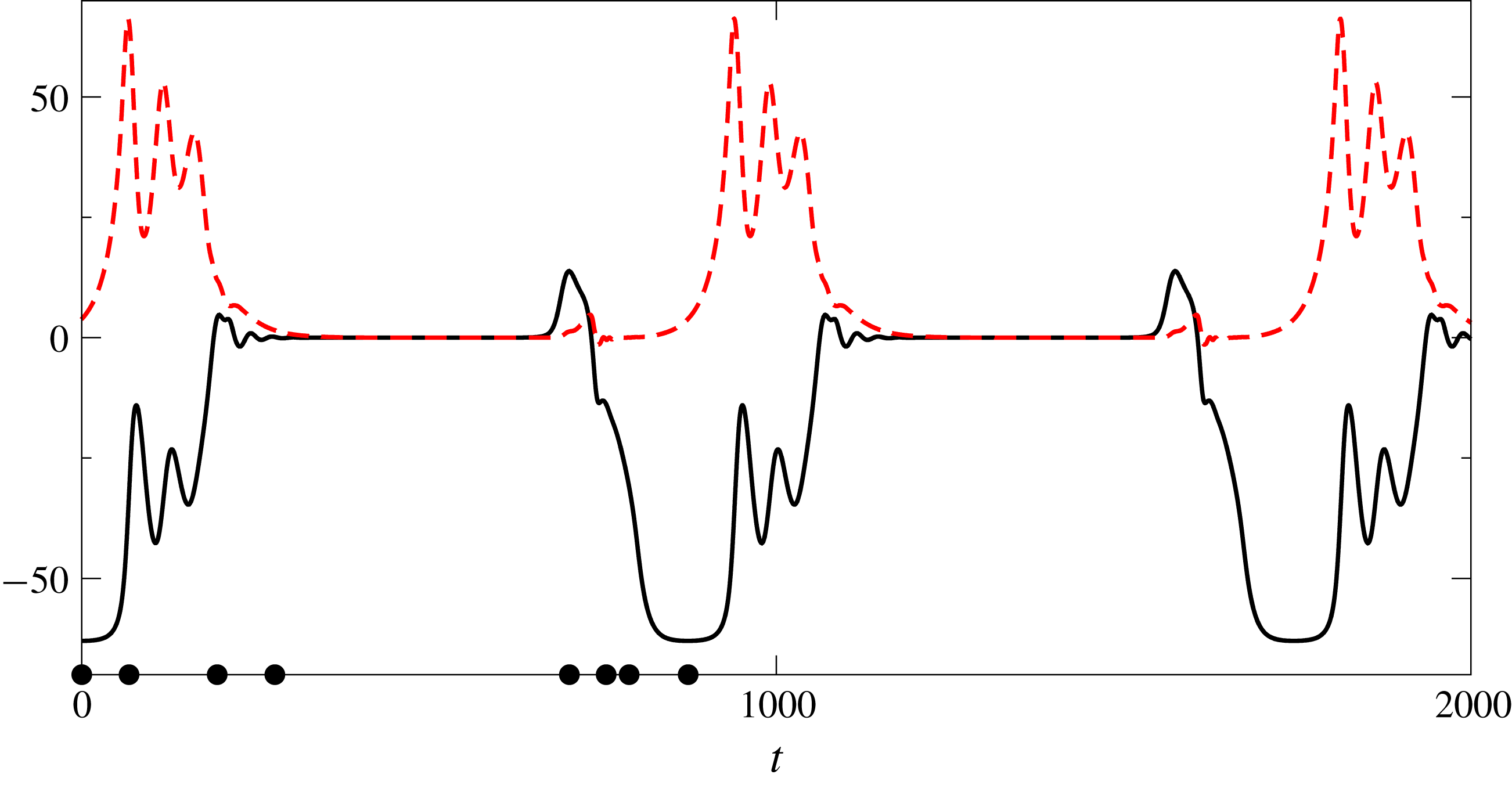
3 Regular OS and SH patterns
According to the previous section (see table 2) one finds as a function of
![]() $\unicode[STIX]{x1D6FE}$
either the OS secondary instability of transverse rolls at
$\unicode[STIX]{x1D6FE}$
either the OS secondary instability of transverse rolls at
![]() $\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{\mathit{OS}}$
or the SH instability at
$\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{\mathit{OS}}$
or the SH instability at
![]() $\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{SH}$
. For
$\unicode[STIX]{x1D716}_{in}=\unicode[STIX]{x1D716}_{SH}$
. For
![]() $\unicode[STIX]{x1D716}\gtrsim \unicode[STIX]{x1D716}_{in}$
the amplitudes of the corresponding destabilizing modes, characterized by the Floquet vectors
$\unicode[STIX]{x1D716}\gtrsim \unicode[STIX]{x1D716}_{in}$
the amplitudes of the corresponding destabilizing modes, characterized by the Floquet vectors
![]() $\boldsymbol{s}_{in}$
, start growing exponentially. They are found to saturate eventually into steady regular 3-D patterns in the nonlinear regime with finite complex amplitudes. As obvious from the stability diagram in figure 3 and the discussion before, the most spectacular
$\boldsymbol{s}_{in}$
, start growing exponentially. They are found to saturate eventually into steady regular 3-D patterns in the nonlinear regime with finite complex amplitudes. As obvious from the stability diagram in figure 3 and the discussion before, the most spectacular
![]() $\unicode[STIX]{x1D6FE}$
-regime is found for
$\unicode[STIX]{x1D6FE}$
-regime is found for
![]() $\unicode[STIX]{x1D6FE}\lesssim \unicode[STIX]{x1D6FE}_{3}=6.169^{\circ }$
, on which we will mainly concentrate in this paper. In the whole interval
$\unicode[STIX]{x1D6FE}\lesssim \unicode[STIX]{x1D6FE}_{3}=6.169^{\circ }$
, on which we will mainly concentrate in this paper. In the whole interval
![]() $\unicode[STIX]{x1D6FE}_{3}<\unicode[STIX]{x1D6FE}\leqq 90^{\circ }$
, where the SH instability prevails, it is sufficient to consider only a few representative examples.
$\unicode[STIX]{x1D6FE}_{3}<\unicode[STIX]{x1D6FE}\leqq 90^{\circ }$
, where the SH instability prevails, it is sufficient to consider only a few representative examples.
The nonlinear evolution of the system for
![]() $\unicode[STIX]{x1D716}>\unicode[STIX]{x1D716}_{in}$
is studied in the present section by DNS of the OBE. In the
$\unicode[STIX]{x1D716}>\unicode[STIX]{x1D716}_{in}$
is studied in the present section by DNS of the OBE. In the
![]() $x{-}y$
plane we use periodic boundary conditions on a rectangle of area
$x{-}y$
plane we use periodic boundary conditions on a rectangle of area
![]() $L_{x}\times L_{y}$
and consequently the calculations are performed in Fourier space (see (2.9)) using a pseudo-spectral method. The
$L_{x}\times L_{y}$
and consequently the calculations are performed in Fourier space (see (2.9)) using a pseudo-spectral method. The
![]() $z$
-dependence of the fields is captured by Galerkin expansions. For the time integration we use the semi-implicit ‘exponential time-differencing method’ as in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) (for some details see appendix A). The results are typically visualized in this paper by the temperature field at the midplane
$z$
-dependence of the fields is captured by Galerkin expansions. For the time integration we use the semi-implicit ‘exponential time-differencing method’ as in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) (for some details see appendix A). The results are typically visualized in this paper by the temperature field at the midplane
![]() $z=0$
, i.e. by the function
$z=0$
, i.e. by the function
![]() $\unicode[STIX]{x1D703}(x,y,z=0,t)$
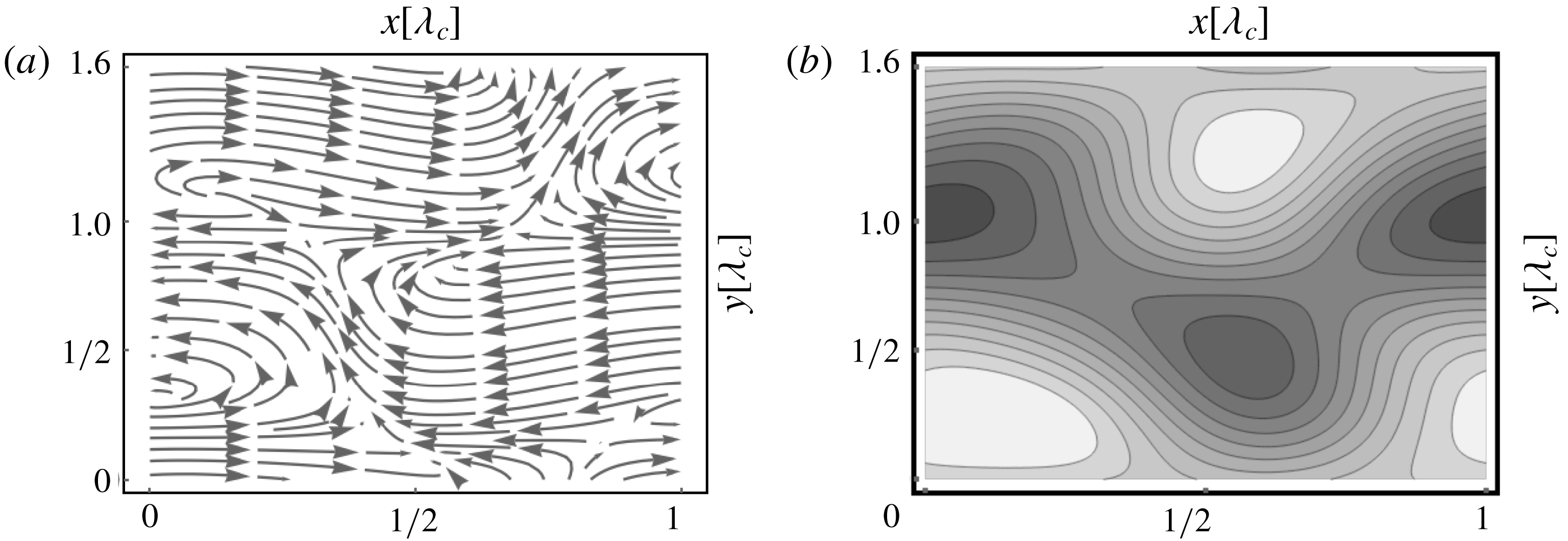
. We use individually scaled 8-bit grey scale images, where lighter areas correspond to positive values and darker ones to negative ones. Thus here and in the following a white stripe stands for a roll pair. In figure 4 we show representative stable steady-state snapshots of
$\unicode[STIX]{x1D703}(x,y,z=0,t)$
. We use individually scaled 8-bit grey scale images, where lighter areas correspond to positive values and darker ones to negative ones. Thus here and in the following a white stripe stands for a roll pair. In figure 4 we show representative stable steady-state snapshots of
![]() $\unicode[STIX]{x1D703}(x,y,z=0,t)$
for different
$\unicode[STIX]{x1D703}(x,y,z=0,t)$
for different
![]() $\unicode[STIX]{x1D6FE}$
calculated with the periodicity lengths
$\unicode[STIX]{x1D6FE}$
calculated with the periodicity lengths
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. They result from DNS started from random initial conditions after the transients have died out. For
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. They result from DNS started from random initial conditions after the transients have died out. For
![]() $\unicode[STIX]{x1D716}<\unicode[STIX]{x1D716}_{in}(\unicode[STIX]{x1D6FE})$
with
$\unicode[STIX]{x1D716}<\unicode[STIX]{x1D716}_{in}(\unicode[STIX]{x1D6FE})$
with
![]() $\unicode[STIX]{x1D6FE}>0^{\circ }$
we arrive always at stable transverse rolls, as shown in figure 4(a). In line with their stability diagram in figure 3 we arrive for
$\unicode[STIX]{x1D6FE}>0^{\circ }$
we arrive always at stable transverse rolls, as shown in figure 4(a). In line with their stability diagram in figure 3 we arrive for
![]() $\unicode[STIX]{x1D716}>\unicode[STIX]{x1D716}_{in}(\unicode[STIX]{x1D6FE})$
either at stationary 3-D SH patterns (see figure 4
b) or at OS patterns in the form of travelling waves along the
$\unicode[STIX]{x1D716}>\unicode[STIX]{x1D716}_{in}(\unicode[STIX]{x1D6FE})$
either at stationary 3-D SH patterns (see figure 4
b) or at OS patterns in the form of travelling waves along the
![]() $y$
-axis (see a snapshot in figure 4
c). The frequency
$y$
-axis (see a snapshot in figure 4
c). The frequency
![]() $\unicode[STIX]{x1D714}$
of the oscillatory patterns is easily obtained by analysing the periodicity in time of
$\unicode[STIX]{x1D714}$
of the oscillatory patterns is easily obtained by analysing the periodicity in time of
![]() $\unicode[STIX]{x1D703}(x,y,z=0,t)$
at fixed
$\unicode[STIX]{x1D703}(x,y,z=0,t)$
at fixed
![]() $x,y$
. It should be noted, that our system, as a consequence of the periodic boundary conditions in the plane, is invariant against translations along the
$x,y$
. It should be noted, that our system, as a consequence of the periodic boundary conditions in the plane, is invariant against translations along the
![]() $x$
- and the
$x$
- and the
![]() $y$
-directions. Thus using different random initial conditions one arrives at different patterns which, however, can be mapped onto each other by shifting the origin of the coordinate system with respect to
$y$
-directions. Thus using different random initial conditions one arrives at different patterns which, however, can be mapped onto each other by shifting the origin of the coordinate system with respect to
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.

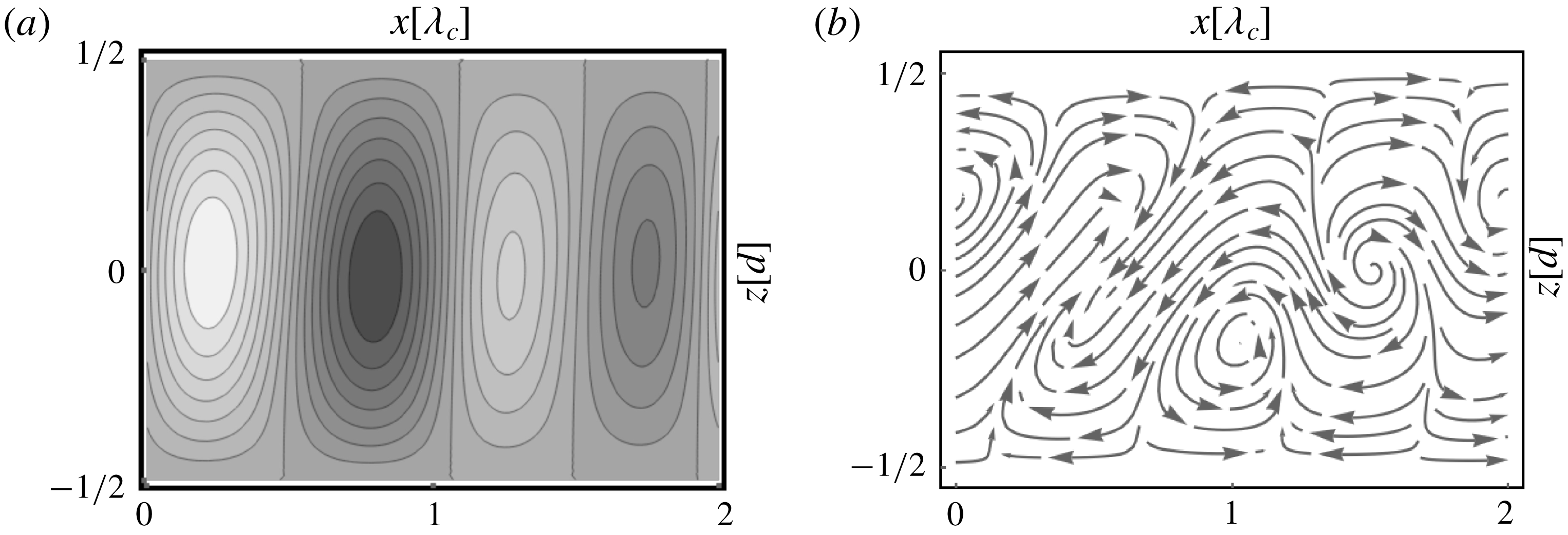
Figure 4. Midplane temperature plots in ILC for
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
: (a) transverse rolls for
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
: (a) transverse rolls for
![]() $\unicode[STIX]{x1D6FE}=3^{\circ }$
. (b) Stationary SH pattern for
$\unicode[STIX]{x1D6FE}=3^{\circ }$
. (b) Stationary SH pattern for
![]() $\unicode[STIX]{x1D6FE}=1.5^{\circ }$
. (c) Snapshot of an OS pattern for
$\unicode[STIX]{x1D6FE}=1.5^{\circ }$
. (c) Snapshot of an OS pattern for
![]() $\unicode[STIX]{x1D6FE}=6^{\circ }$
(for details see text).
$\unicode[STIX]{x1D6FE}=6^{\circ }$
(for details see text).
Inspection of such pictures yields immediately the dominant wavelengths
![]() $\unicode[STIX]{x1D706}_{x}$
and
$\unicode[STIX]{x1D706}_{x}$
and
![]() $\unicode[STIX]{x1D706}_{y}$
characterizing the spatial periodicity of the patterns in the
$\unicode[STIX]{x1D706}_{y}$
characterizing the spatial periodicity of the patterns in the
![]() $x{-}y$
plane. Note that as a consequence of our periodic boundary conditions in the plane the wavelengths
$x{-}y$
plane. Note that as a consequence of our periodic boundary conditions in the plane the wavelengths
![]() $\unicode[STIX]{x1D706}_{x}$
,
$\unicode[STIX]{x1D706}_{x}$
,
![]() $\unicode[STIX]{x1D706}_{y}$
must be integer fractions of
$\unicode[STIX]{x1D706}_{y}$
must be integer fractions of
![]() $L_{x}$
and
$L_{x}$
and
![]() $L_{y}$
, respectively. In the
$L_{y}$
, respectively. In the
![]() $x$
-direction all DNS have obviously locked into
$x$
-direction all DNS have obviously locked into
![]() $\unicode[STIX]{x1D706}_{x}=L_{x}/8=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
, corresponding to 8 roll pairs. The critical wavelength
$\unicode[STIX]{x1D706}_{x}=L_{x}/8=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
, corresponding to 8 roll pairs. The critical wavelength
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2\unicode[STIX]{x03C0}/q_{c}(\unicode[STIX]{x1D6FE})\sim 2$
is determined by
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2\unicode[STIX]{x03C0}/q_{c}(\unicode[STIX]{x1D6FE})\sim 2$
is determined by
![]() $q_{c}(\unicode[STIX]{x1D6FE})$
from table 1 or 2. The theoretical value of
$q_{c}(\unicode[STIX]{x1D6FE})$
from table 1 or 2. The theoretical value of
![]() $\unicode[STIX]{x1D706}_{c}$
must be reflected in the experimental roll patterns observed in large-aspect-ratio systems, when slowly increasing
$\unicode[STIX]{x1D706}_{c}$
must be reflected in the experimental roll patterns observed in large-aspect-ratio systems, when slowly increasing
![]() $R$
until it crosses
$R$
until it crosses
![]() $R_{c}$
. Further increasing
$R_{c}$
. Further increasing
![]() $R$
should then reveal the secondary instabilities of the rolls as well. This has been indeed confirmed for instance in RBC with
$R$
should then reveal the secondary instabilities of the rolls as well. This has been indeed confirmed for instance in RBC with
![]() $\Pr \approx 1$
(see Bodenschatz et al. (Reference Bodenschatz, Pesch and Ahlers2000) and references therein).
$\Pr \approx 1$
(see Bodenschatz et al. (Reference Bodenschatz, Pesch and Ahlers2000) and references therein).
The wavelength
![]() $\unicode[STIX]{x1D706}_{y}$
has locked into a value
$\unicode[STIX]{x1D706}_{y}$
has locked into a value
![]() $\unicode[STIX]{x1D706}_{y}=L_{y}/m$
with an integer
$\unicode[STIX]{x1D706}_{y}=L_{y}/m$
with an integer
![]() $m$
. Not surprisingly we find in all our simulations that
$m$
. Not surprisingly we find in all our simulations that
![]() $m$
is chosen by the system such that
$m$
is chosen by the system such that
![]() $\unicode[STIX]{x1D706}_{y}$
is in the vicinity of
$\unicode[STIX]{x1D706}_{y}$
is in the vicinity of
![]() $\unicode[STIX]{x1D706}_{y}^{in}=2\unicode[STIX]{x03C0}/s_{y}^{in}$
, where the values of
$\unicode[STIX]{x1D706}_{y}^{in}=2\unicode[STIX]{x03C0}/s_{y}^{in}$
, where the values of
![]() $s_{y}^{in}$
are given in table 2. This selection process has been validated by DNS with different
$s_{y}^{in}$
are given in table 2. This selection process has been validated by DNS with different
![]() $L_{y}$
. In general, larger values of
$L_{y}$
. In general, larger values of
![]() $L_{y}$
give the system more flexibility in selecting
$L_{y}$
give the system more flexibility in selecting
![]() $m$
. Thus we have performed some even more time-consuming simulations for larger periodicity areas in the
$m$
. Thus we have performed some even more time-consuming simulations for larger periodicity areas in the
![]() $x{-}y$
plane with
$x{-}y$
plane with
![]() $L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. As demonstrated in figure 5 we arrive indeed, starting from random initial conditions, at the common basic patterns already shown in figure 4. The SH pattern (see figure 5
b) for
$L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. As demonstrated in figure 5 we arrive indeed, starting from random initial conditions, at the common basic patterns already shown in figure 4. The SH pattern (see figure 5
b) for
![]() $\unicode[STIX]{x1D6FE}=50^{\circ }$
has locked into
$\unicode[STIX]{x1D6FE}=50^{\circ }$
has locked into
![]() $\unicode[STIX]{x1D706}_{y}=L_{x}/9$
, such that
$\unicode[STIX]{x1D706}_{y}=L_{x}/9$
, such that
![]() $s_{y}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{y}=1.541$
matches very well
$s_{y}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{y}=1.541$
matches very well
![]() $s_{y}^{SH}=1.574$
in table 2. In figure 5(c) we show an OS pattern for
$s_{y}^{SH}=1.574$
in table 2. In figure 5(c) we show an OS pattern for
![]() $\unicode[STIX]{x1D6FE}=5^{\circ }$
, which has locked into
$\unicode[STIX]{x1D6FE}=5^{\circ }$
, which has locked into
![]() $\unicode[STIX]{x1D706}_{y}=L_{x}/11$
corresponding to
$\unicode[STIX]{x1D706}_{y}=L_{x}/11$
corresponding to
![]() $s_{y}=2.053$
near to
$s_{y}=2.053$
near to
![]() $s_{y}^{\mathit{OS}}=1.961$
in table 2. Although in this context choosing large values of
$s_{y}^{\mathit{OS}}=1.961$
in table 2. Although in this context choosing large values of
![]() $L_{x},L_{y}$
would be desirable, this is in general hardly possible in practice due to the fast increase of computer time.
$L_{x},L_{y}$
would be desirable, this is in general hardly possible in practice due to the fast increase of computer time.

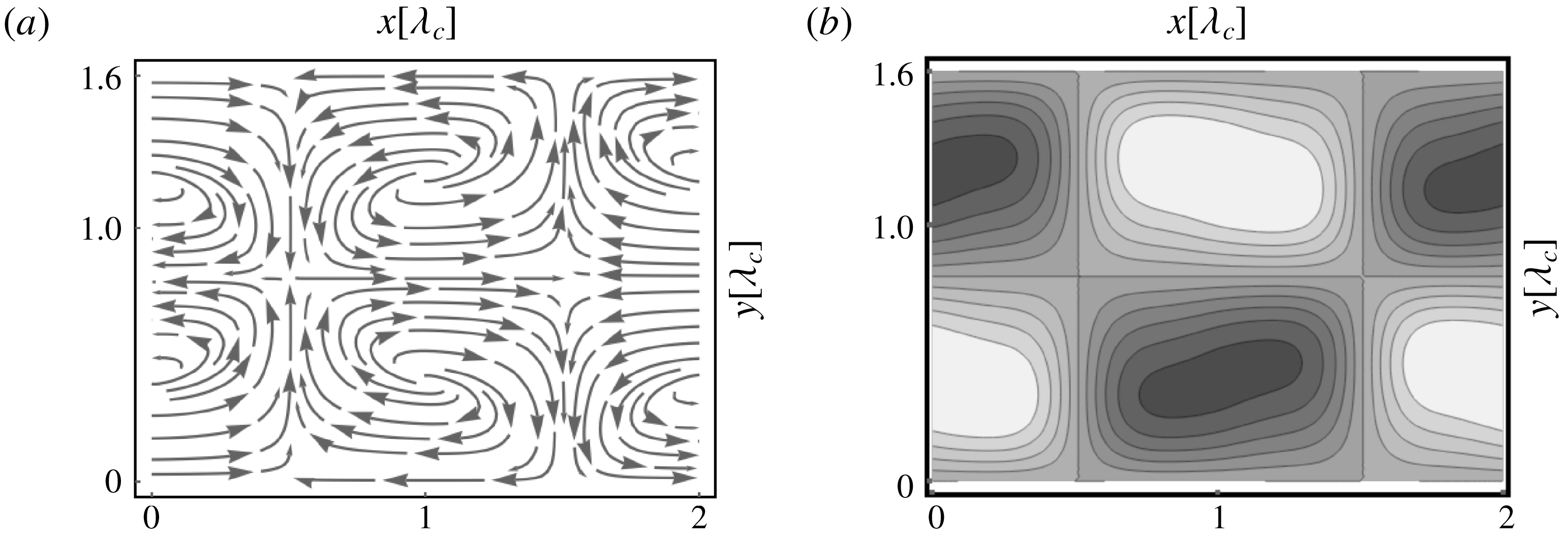
Figure 5. Basic patterns as in figure 4 for larger
![]() $L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
: (a) transverse rolls for
$L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
: (a) transverse rolls for
![]() $\unicode[STIX]{x1D6FE}=50^{\circ }$
,
$\unicode[STIX]{x1D6FE}=50^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.03$
,
$\unicode[STIX]{x1D716}=0.03$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.8576$
with
$\unicode[STIX]{x1D716}_{0}=-0.8576$
with
![]() $\unicode[STIX]{x1D706}_{c}=2.293$
. (b) SH pattern for
$\unicode[STIX]{x1D706}_{c}=2.293$
. (b) SH pattern for
![]() $\unicode[STIX]{x1D6FE}=50^{\circ }$
,
$\unicode[STIX]{x1D6FE}=50^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.045>0.037=\unicode[STIX]{x1D716}_{SH}$
,
$\unicode[STIX]{x1D716}=0.045>0.037=\unicode[STIX]{x1D716}_{SH}$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.8556$
. (c) Snapshot of an OS pattern for
$\unicode[STIX]{x1D716}_{0}=-0.8556$
. (c) Snapshot of an OS pattern for
![]() $\unicode[STIX]{x1D6FE}=5^{\circ }$
,
$\unicode[STIX]{x1D6FE}=5^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.055>0.049=\unicode[STIX]{x1D716}_{\mathit{OS}}$
,
$\unicode[STIX]{x1D716}=0.055>0.049=\unicode[STIX]{x1D716}_{\mathit{OS}}$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.2859$
with
$\unicode[STIX]{x1D716}_{0}=-0.2859$
with
![]() $\unicode[STIX]{x1D706}_{c}=2.104$
(for details, see text).
$\unicode[STIX]{x1D706}_{c}=2.104$
(for details, see text).
Finally it is obvious that the values of
![]() $\boldsymbol{q}_{c}$
and
$\boldsymbol{q}_{c}$
and
![]() $R_{c}$
depend on the real lateral boundary conditions for systems with smaller lateral extensions or different geometries. Typically in analysing experiments one uses thus the experimental value of
$R_{c}$
depend on the real lateral boundary conditions for systems with smaller lateral extensions or different geometries. Typically in analysing experiments one uses thus the experimental value of
![]() $R_{c}$
to calculate the relative distance
$R_{c}$
to calculate the relative distance
![]() $\unicode[STIX]{x1D716}$
(2.12) of
$\unicode[STIX]{x1D716}$
(2.12) of
![]() $R$
from onset and measures the wave vectors
$R$
from onset and measures the wave vectors
![]() $\boldsymbol{q}$
in units of
$\boldsymbol{q}$
in units of
![]() $|\boldsymbol{q}_{c}|$
. In this way the results obtained via the bifurcation approach match much better the experimental ones.
$|\boldsymbol{q}_{c}|$
. In this way the results obtained via the bifurcation approach match much better the experimental ones.
In the following sections we will discuss the regular SH and OS patterns in more detail.
3.1 SH patterns
The SH patterns bifurcate from the transverse rolls for
![]() $\unicode[STIX]{x1D6FE}$
in the intervals
$\unicode[STIX]{x1D6FE}$
in the intervals
![]() $1.023^{\circ }<\unicode[STIX]{x1D6FE}<2.183^{\circ }$
and
$1.023^{\circ }<\unicode[STIX]{x1D6FE}<2.183^{\circ }$
and
![]() $6.169^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$
. In line with the discussion of the SH instability in § 2.3 their dominant Fourier coefficients belong to the wave vectors
$6.169^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$
. In line with the discussion of the SH instability in § 2.3 their dominant Fourier coefficients belong to the wave vectors
![]() $\pm \boldsymbol{q}_{i}$
,
$\pm \boldsymbol{q}_{i}$
,
![]() $i=1,2,3$
in Fourier space where
$i=1,2,3$
in Fourier space where
![]() $\boldsymbol{q}_{1}=(q_{c},0)$
,
$\boldsymbol{q}_{1}=(q_{c},0)$
,
![]() $\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y})$
, with
$\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y})$
, with
![]() $s_{y}\approx s_{y}^{SH}$
given in table 2. In figure 6 we show for three values of
$s_{y}\approx s_{y}^{SH}$
given in table 2. In figure 6 we show for three values of
![]() $\unicode[STIX]{x1D6FE}=1.5^{\circ }$
,
$\unicode[STIX]{x1D6FE}=1.5^{\circ }$
,
![]() $50^{\circ }$
,
$50^{\circ }$
,
![]() $90^{\circ }$
representative examples of the time independent midplane temperature field
$90^{\circ }$
representative examples of the time independent midplane temperature field
![]() $\unicode[STIX]{x1D703}(x,y)$
in (3.1), where we used
$\unicode[STIX]{x1D703}(x,y)$
in (3.1), where we used
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. The subharmonic nature of the patterns, where the teeth are shifted by
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. The subharmonic nature of the patterns, where the teeth are shifted by
![]() $\unicode[STIX]{x1D706}_{y}/2$
after moving by
$\unicode[STIX]{x1D706}_{y}/2$
after moving by
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
in the
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
in the
![]() $x$
-direction is obvious. In all our simulations the teeth of the SH patterns have pointed to the right for
$x$
-direction is obvious. In all our simulations the teeth of the SH patterns have pointed to the right for
![]() $1.023^{\circ }<\unicode[STIX]{x1D6FE}<2.183^{\circ }$
opposite to their orientation for
$1.023^{\circ }<\unicode[STIX]{x1D6FE}<2.183^{\circ }$
opposite to their orientation for
![]() $6.169^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$
.
$6.169^{\circ }<\unicode[STIX]{x1D6FE}<90^{\circ }$
.

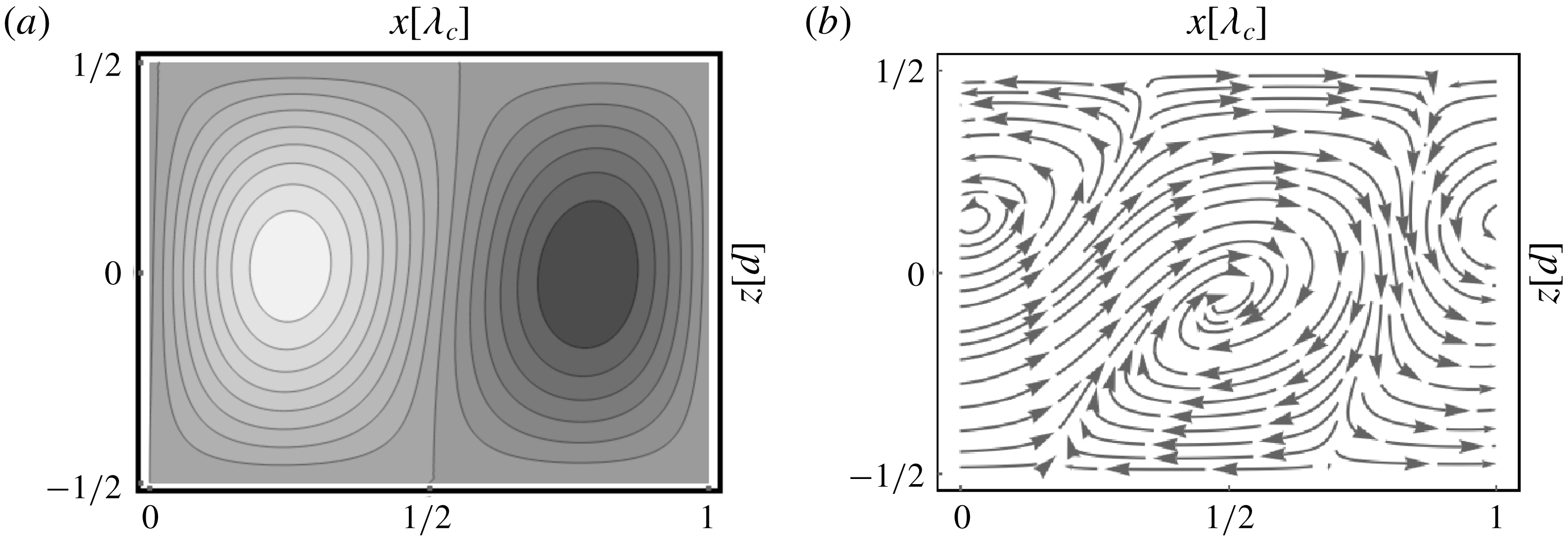
Figure 6. Temperature plots of SH patterns for
![]() $Pr=0.025$
and different
$Pr=0.025$
and different
![]() $\unicode[STIX]{x1D6FE}$
: (a)
$\unicode[STIX]{x1D6FE}$
: (a)
![]() $\unicode[STIX]{x1D6FE}=1.5^{\circ }$
,
$\unicode[STIX]{x1D6FE}=1.5^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.12$
,
$\unicode[STIX]{x1D716}=0.12$
,
![]() $\unicode[STIX]{x1D716}_{0}=0.0522$
, (b)
$\unicode[STIX]{x1D716}_{0}=0.0522$
, (b)
![]() $\unicode[STIX]{x1D6FE}=50^{\circ }$
,
$\unicode[STIX]{x1D6FE}=50^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.05$
,
$\unicode[STIX]{x1D716}=0.05$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.85487$
, (c)
$\unicode[STIX]{x1D716}_{0}=-0.85487$
, (c)
![]() $\unicode[STIX]{x1D6FE}=90^{\circ }$
,
$\unicode[STIX]{x1D6FE}=90^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.06$
,
$\unicode[STIX]{x1D716}=0.06$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.88128$
.
$\unicode[STIX]{x1D716}_{0}=-0.88128$
.
In the following we discuss the 3-D character of the SH patterns in more detail using
![]() $\unicode[STIX]{x1D6FE}=10^{\circ }$
and
$\unicode[STIX]{x1D6FE}=10^{\circ }$
and
![]() $\unicode[STIX]{x1D716}=0.05$
as a representative example. All pictures have been produced with Mathematica. First we show a 3-D contour plot of the temperature field
$\unicode[STIX]{x1D716}=0.05$
as a representative example. All pictures have been produced with Mathematica. First we show a 3-D contour plot of the temperature field
![]() $\unicode[STIX]{x1D703}(x,y,z)$
in figure 7, according to which the SH instability leads to a
$\unicode[STIX]{x1D703}(x,y,z)$
in figure 7, according to which the SH instability leads to a
![]() $y$
-periodic bulging out of the original transverse rolls. In figures 7(b) and 8(a) we show the corresponding 2-D plots of
$y$
-periodic bulging out of the original transverse rolls. In figures 7(b) and 8(a) we show the corresponding 2-D plots of
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
at the midplane and of
$\unicode[STIX]{x1D703}(x,y,z=0)$
at the midplane and of
![]() $\unicode[STIX]{x1D703}(x,y=0,z)$
in the
$\unicode[STIX]{x1D703}(x,y=0,z)$
in the
![]() $x{-}z$
-plane at
$x{-}z$
-plane at
![]() $y=0$
. Due to the subharmonic character of the bifurcation the spatial periodicity of the pattern in
$y=0$
. Due to the subharmonic character of the bifurcation the spatial periodicity of the pattern in
![]() $x$
corresponds to the wavelength
$x$
corresponds to the wavelength
![]() $2\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
.
$2\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
.
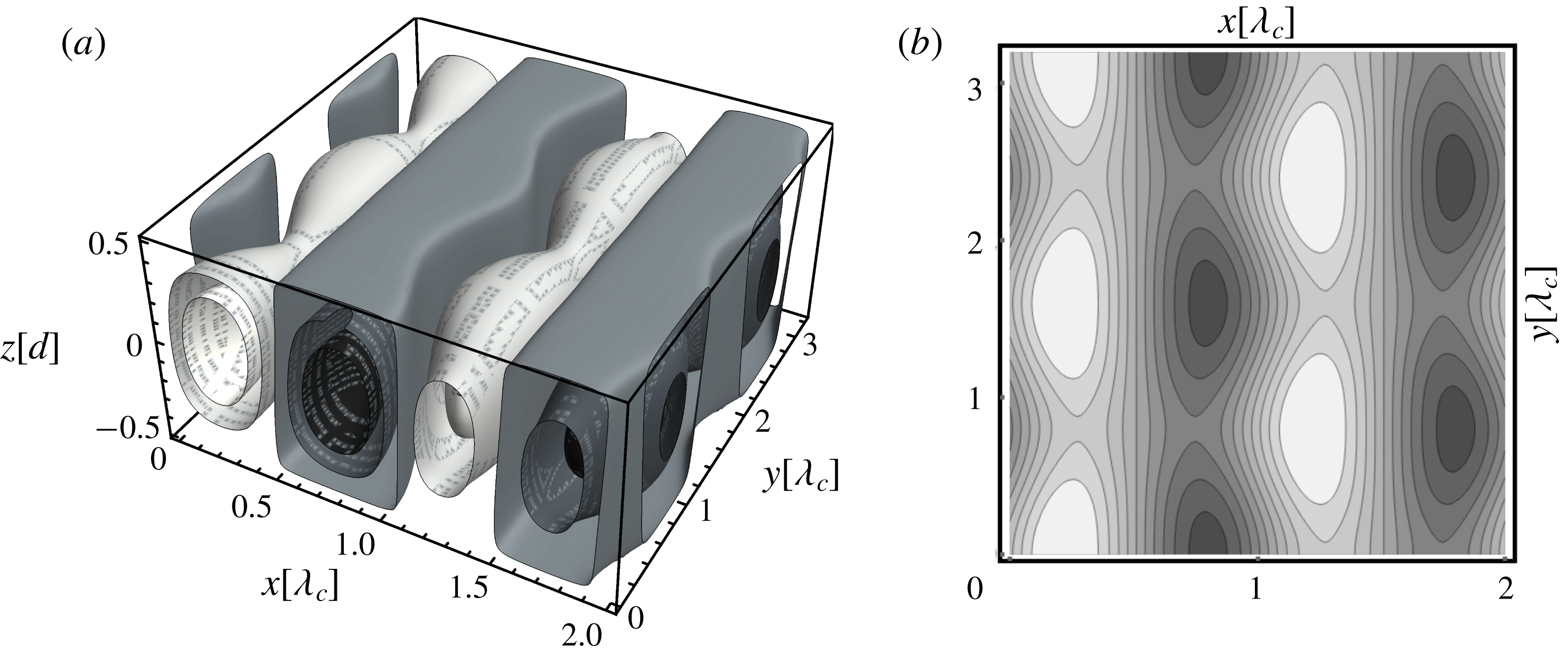
Figure 7. DNS for
![]() $\unicode[STIX]{x1D6FE}=10^{\circ }$
,
$\unicode[STIX]{x1D6FE}=10^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.05$
,
$\unicode[STIX]{x1D716}=0.05$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.522145$
,
$\unicode[STIX]{x1D716}_{0}=-0.522145$
,
![]() $\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2.175d$
with the periodicity lengths
$\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2.175d$
with the periodicity lengths
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{x}$
: (a) 3-D contour plot of
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{x}$
: (a) 3-D contour plot of
![]() $\unicode[STIX]{x1D703}(x,y,z)$
for
$\unicode[STIX]{x1D703}(x,y,z)$
for
![]() $0\leqq x\leqq 2\unicode[STIX]{x1D706}_{x}$
,
$0\leqq x\leqq 2\unicode[STIX]{x1D706}_{x}$
,
![]() $0\leqq y\leqq 2\unicode[STIX]{x1D706}_{y}=2(8/5)\unicode[STIX]{x1D706}_{x}$
; (b) 2-D contour plot of the midplane temperature
$0\leqq y\leqq 2\unicode[STIX]{x1D706}_{y}=2(8/5)\unicode[STIX]{x1D706}_{x}$
; (b) 2-D contour plot of the midplane temperature
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
from panel (a).
$\unicode[STIX]{x1D703}(x,y,z=0)$
from panel (a).
The velocity field (see (2.4)) is much more complex and we have been unable to produce appealing 3-D plots. So we show in figure 8(b) a streamplot of
![]() $(v_{x},v_{z})$
obtained from (2.4) in the
$(v_{x},v_{z})$
obtained from (2.4) in the
![]() $x{-}z$
plane. According to figure 8(a) we expect a buoyancy driven upward flow at
$x{-}z$
plane. According to figure 8(a) we expect a buoyancy driven upward flow at
![]() $x=1/4$
, where
$x=1/4$
, where
![]() $\unicode[STIX]{x1D703}$
is maximal at
$\unicode[STIX]{x1D703}$
is maximal at
![]() $z=0$
and analogously a downward flow at
$z=0$
and analogously a downward flow at
![]() $x=3/4$
. This applies analogously to
$x=3/4$
. This applies analogously to
![]() $x=1.25$
and
$x=1.25$
and
![]() $x=1.75$
. For standard RBC the flow would be
$x=1.75$
. For standard RBC the flow would be
![]() $y$
-independent and parallel to the
$y$
-independent and parallel to the
![]() $z$
-axis at those
$z$
-axis at those
![]() $x$
values between
$x$
values between
![]() $z=1/2$
and
$z=1/2$
and
![]() $z=-1/2$
. In contrast, the streamlines turn here towards the
$z=-1/2$
. In contrast, the streamlines turn here towards the
![]() $x$
-direction and develop even small vortices. The additional temperature variations in the
$x$
-direction and develop even small vortices. The additional temperature variations in the
![]() $x{-}y$
-plane (see figure 7
b) drive also a flow with
$x{-}y$
-plane (see figure 7
b) drive also a flow with
![]() $v_{y}\neq 0$
. This is documented by the
$v_{y}\neq 0$
. This is documented by the
![]() $(v_{x},v_{y})$
streamlines in figure 9(a). The clearly visible vortices are immediately identified by the contour plot of the vertical vorticity
$(v_{x},v_{y})$
streamlines in figure 9(a). The clearly visible vortices are immediately identified by the contour plot of the vertical vorticity
![]() $(\unicode[STIX]{x1D735}\times \boldsymbol{v})_{z}$
in figure 9(b). Note that the subharmonic nature of the bifurcation is here also reflected in the difference between the velocity vector field in the intervals
$(\unicode[STIX]{x1D735}\times \boldsymbol{v})_{z}$
in figure 9(b). Note that the subharmonic nature of the bifurcation is here also reflected in the difference between the velocity vector field in the intervals
![]() $0<x<\unicode[STIX]{x1D706}_{x}$
and
$0<x<\unicode[STIX]{x1D706}_{x}$
and
![]() $\unicode[STIX]{x1D706}_{x}<x<2\unicode[STIX]{x1D706}_{x}$
and also in a small opposite rotation about the
$\unicode[STIX]{x1D706}_{x}<x<2\unicode[STIX]{x1D706}_{x}$
and also in a small opposite rotation about the
![]() $z$
-axis of the white and black ‘lenses’ in the vorticity plot.
$z$
-axis of the white and black ‘lenses’ in the vorticity plot.
In the following we will demonstrate that the temperature field
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
at the midplane shown in figure 7(b) is very useful to characterize the SH pattern in more detail. Our starting point is the 2-D Fourier representation of
$\unicode[STIX]{x1D703}(x,y,z=0)$
at the midplane shown in figure 7(b) is very useful to characterize the SH pattern in more detail. Our starting point is the 2-D Fourier representation of
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
where the Fourier coefficents with wavevectors
$\unicode[STIX]{x1D703}(x,y,z=0)$
where the Fourier coefficents with wavevectors
![]() $\boldsymbol{q}_{1}=(q_{c},0)$
(for the transverse rolls) and
$\boldsymbol{q}_{1}=(q_{c},0)$
(for the transverse rolls) and
![]() $\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y})$
with
$\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y})$
with
![]() $s_{y}\approx s_{y}^{SH}$
(characterizing the SH instability), are dominant according to § 2.3. In fact, when calculating
$s_{y}\approx s_{y}^{SH}$
(characterizing the SH instability), are dominant according to § 2.3. In fact, when calculating
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
using only this wave vector subset, one obtains a function
$\unicode[STIX]{x1D703}(x,y,z=0)$
using only this wave vector subset, one obtains a function
![]() $h(x,y)$
, which yields a very useful and accurate approximation of
$h(x,y)$
, which yields a very useful and accurate approximation of
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
: a plot of
$\unicode[STIX]{x1D703}(x,y,z=0)$
: a plot of
![]() $h(x,y)$
looks practically identical to figure 7(b) for not too large
$h(x,y)$
looks practically identical to figure 7(b) for not too large
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
The phases of the Fourier coefficients associated with the wave vectors
![]() $\boldsymbol{q}_{1,2,3}$
defined above fulfil always a special relation detailed in § B.1, which we use as the general signature of SH patterns. As a consequence the function
$\boldsymbol{q}_{1,2,3}$
defined above fulfil always a special relation detailed in § B.1, which we use as the general signature of SH patterns. As a consequence the function
![]() $h(x,y)$
, after a suitable shift of the
$h(x,y)$
, after a suitable shift of the
![]() $x,y$
-coordinate system can be always written in a form which depends only on two real amplitudes
$x,y$
-coordinate system can be always written in a form which depends only on two real amplitudes
![]() $A_{0}>0,B_{0}>0$
,
$A_{0}>0,B_{0}>0$
,
There is a discrete symmetry breaking involved; for
![]() $\mathfrak{a}=-1$
the ‘teeth’ point to the right as in the figure 4(b) and for
$\mathfrak{a}=-1$
the ‘teeth’ point to the right as in the figure 4(b) and for
![]() $\mathfrak{a}=1$
to the left.
$\mathfrak{a}=1$
to the left.
Table 3. Left table: amplitudes
![]() $A_{0}$
,
$A_{0}$
,
![]() $B_{0}$
of SH-patterns (see (3.1)) for different
$B_{0}$
of SH-patterns (see (3.1)) for different
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $\unicode[STIX]{x1D716}$
and
$\unicode[STIX]{x1D716}$
and
![]() $s_{y}$
in the DNS. Near the bold/underlined
$s_{y}$
in the DNS. Near the bold/underlined
![]() $\unicode[STIX]{x1D6FE}$
values with the corresponding wavenumbers
$\unicode[STIX]{x1D6FE}$
values with the corresponding wavenumbers
![]() $s_{y}$
the amplitudes
$s_{y}$
the amplitudes
![]() $B_{0}$
are maximal (for details see text). Right table: the analogous data for travelling waves; in addition their frequency
$B_{0}$
are maximal (for details see text). Right table: the analogous data for travelling waves; in addition their frequency
![]() $\unicode[STIX]{x1D714}$
is listed in comparison with
$\unicode[STIX]{x1D714}$
is listed in comparison with
![]() $\unicode[STIX]{x1D714}_{0}$
at the onset of the OS instability (see table 2).
$\unicode[STIX]{x1D714}_{0}$
at the onset of the OS instability (see table 2).
The SH solutions exist for
![]() $\unicode[STIX]{x1D716}>\unicode[STIX]{x1D716}_{SH}$
(see table 2). The amplitude
$\unicode[STIX]{x1D716}>\unicode[STIX]{x1D716}_{SH}$
(see table 2). The amplitude
![]() $B_{0}$
depends on
$B_{0}$
depends on
![]() $\unicode[STIX]{x1D6FE}$
and rises continuously with increasing
$\unicode[STIX]{x1D6FE}$
and rises continuously with increasing
![]() $\unicode[STIX]{x1D716}-\unicode[STIX]{x1D716}_{SH}$
, while for
$\unicode[STIX]{x1D716}-\unicode[STIX]{x1D716}_{SH}$
, while for
![]() $0<\unicode[STIX]{x1D716}<\unicode[STIX]{x1D716}_{SH}$
we have simple transverse rolls with
$0<\unicode[STIX]{x1D716}<\unicode[STIX]{x1D716}_{SH}$
we have simple transverse rolls with
![]() $B_{0}=0$
and
$B_{0}=0$
and
![]() $A_{0}\propto \sqrt{\unicode[STIX]{x1D716}}$
. Some characteristic data of our DNS have been collected in table 3 for different
$A_{0}\propto \sqrt{\unicode[STIX]{x1D716}}$
. Some characteristic data of our DNS have been collected in table 3 for different
![]() $\unicode[STIX]{x1D6FE}$
, where always
$\unicode[STIX]{x1D6FE}$
, where always
![]() $L_{x}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
was chosen. In contrast, we have used different periodicity lengths
$L_{x}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
was chosen. In contrast, we have used different periodicity lengths
![]() $L_{y}$
in the DNS, which then have locked into different values of the wavelength
$L_{y}$
in the DNS, which then have locked into different values of the wavelength
![]() $\unicode[STIX]{x1D706}_{y}=L_{y}/m$
, i.e. of the wavenumber
$\unicode[STIX]{x1D706}_{y}=L_{y}/m$
, i.e. of the wavenumber
![]() $s_{y}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{y}$
(see table 3). Here for each
$s_{y}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{y}$
(see table 3). Here for each
![]() $\unicode[STIX]{x1D6FE}$
two data sets have been emphasized: the first set (
$\unicode[STIX]{x1D6FE}$
two data sets have been emphasized: the first set (
![]() $\unicode[STIX]{x1D6FE}$
in bold) corresponds to DNS with our standard choice
$\unicode[STIX]{x1D6FE}$
in bold) corresponds to DNS with our standard choice
![]() $L_{y}=L_{x}$
while in the second one (
$L_{y}=L_{x}$
while in the second one (
![]() $\unicode[STIX]{x1D6FE}$
underlined) values of
$\unicode[STIX]{x1D6FE}$
underlined) values of
![]() $L_{y}$
, slightly different from
$L_{y}$
, slightly different from
![]() $L_{x}$
, have been chosen, such that
$L_{x}$
, have been chosen, such that
![]() $s_{y}=s_{y}^{SH}$
. In vicinity of these
$s_{y}=s_{y}^{SH}$
. In vicinity of these
![]() $s_{y}$
values the amplitude
$s_{y}$
values the amplitude
![]() $B_{0}$
is found to be maximal, which means that the secondary SH instability is most effective.
$B_{0}$
is found to be maximal, which means that the secondary SH instability is most effective.
3.2 OS patterns
In our DNS, starting from random initial conditions, we arrive eventually always at stable travelling-wave patterns. In figure 4(c) we have shown a representative snapshot for
![]() $\unicode[STIX]{x1D6FE}=6^{\circ }$
at
$\unicode[STIX]{x1D6FE}=6^{\circ }$
at
![]() $\unicode[STIX]{x1D716}=0.058$
which originates from the oscillatory instability at
$\unicode[STIX]{x1D716}=0.058$
which originates from the oscillatory instability at
![]() $\unicode[STIX]{x1D716}_{\mathit{OS}}=0.051$
with
$\unicode[STIX]{x1D716}_{\mathit{OS}}=0.051$
with
![]() $s_{y}^{\mathit{OS}}=1.929$
and
$s_{y}^{\mathit{OS}}=1.929$
and
![]() $\unicode[STIX]{x1D714}_{0}=0.402$
(see table 2). The simulations have locked into
$\unicode[STIX]{x1D714}_{0}=0.402$
(see table 2). The simulations have locked into
![]() $\unicode[STIX]{x1D706}_{y}=8/5\unicode[STIX]{x1D706}_{c}$
, i.e. into
$\unicode[STIX]{x1D706}_{y}=8/5\unicode[STIX]{x1D706}_{c}$
, i.e. into
![]() $s_{y}=1.850$
, with
$s_{y}=1.850$
, with
![]() $\unicode[STIX]{x1D714}=0.4002$
, which is near
$\unicode[STIX]{x1D714}=0.4002$
, which is near
![]() $\unicode[STIX]{x1D714}_{0}$
. In general, we are confronted in our DNS with very long transients often of the order of
$\unicode[STIX]{x1D714}_{0}$
. In general, we are confronted in our DNS with very long transients often of the order of
![]() $1000t_{v}$
or more. During that time interval the oscillatory patterns resemble, however, standing-wave ones, to which we return later in this section.
$1000t_{v}$
or more. During that time interval the oscillatory patterns resemble, however, standing-wave ones, to which we return later in this section.
Our basic equations are invariant against the reflection
![]() $y\rightarrow -y$
. This symmetry is spontaneously broken in travelling-wave patterns which move either upwards along
$y\rightarrow -y$
. This symmetry is spontaneously broken in travelling-wave patterns which move either upwards along
![]() $y$
with a phase velocity
$y$
with a phase velocity
![]() $v_{phas}$
or downwards with
$v_{phas}$
or downwards with
![]() $-v_{phas}$
. When transforming the basic equations with
$-v_{phas}$
. When transforming the basic equations with
![]() $y\rightarrow y-(+)v_{phas}t$
for the first (second) case into the comoving frame, the resulting DNS produce essentially equivalent stationary patterns. According to the 3-D contour plot of
$y\rightarrow y-(+)v_{phas}t$
for the first (second) case into the comoving frame, the resulting DNS produce essentially equivalent stationary patterns. According to the 3-D contour plot of
![]() $\unicode[STIX]{x1D703}(x,y,z)$
in figure 10(a) we deal again with deformed convection rolls. In contrast to the SH patterns they bulge out symmetrically to the left and to the right along the
$\unicode[STIX]{x1D703}(x,y,z)$
in figure 10(a) we deal again with deformed convection rolls. In contrast to the SH patterns they bulge out symmetrically to the left and to the right along the
![]() $x$
direction when moving along
$x$
direction when moving along
![]() $y$
. The wavelength
$y$
. The wavelength
![]() $\unicode[STIX]{x1D706}_{x}$
is given as
$\unicode[STIX]{x1D706}_{x}$
is given as
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
, while
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
, while
![]() $\unicode[STIX]{x1D706}_{y}=8/5\unicode[STIX]{x1D706}_{x}$
holds as evident from the plot of
$\unicode[STIX]{x1D706}_{y}=8/5\unicode[STIX]{x1D706}_{x}$
holds as evident from the plot of
![]() $\unicode[STIX]{x1D703}$
in the
$\unicode[STIX]{x1D703}$
in the
![]() $x{-}y$
plane in figure 10(b). We leave out a detailed discussion of the velocity field shown in figures 11 and 12 since one finds only quantitative differences compared to the SH patterns in the previous section.
$x{-}y$
plane in figure 10(b). We leave out a detailed discussion of the velocity field shown in figures 11 and 12 since one finds only quantitative differences compared to the SH patterns in the previous section.
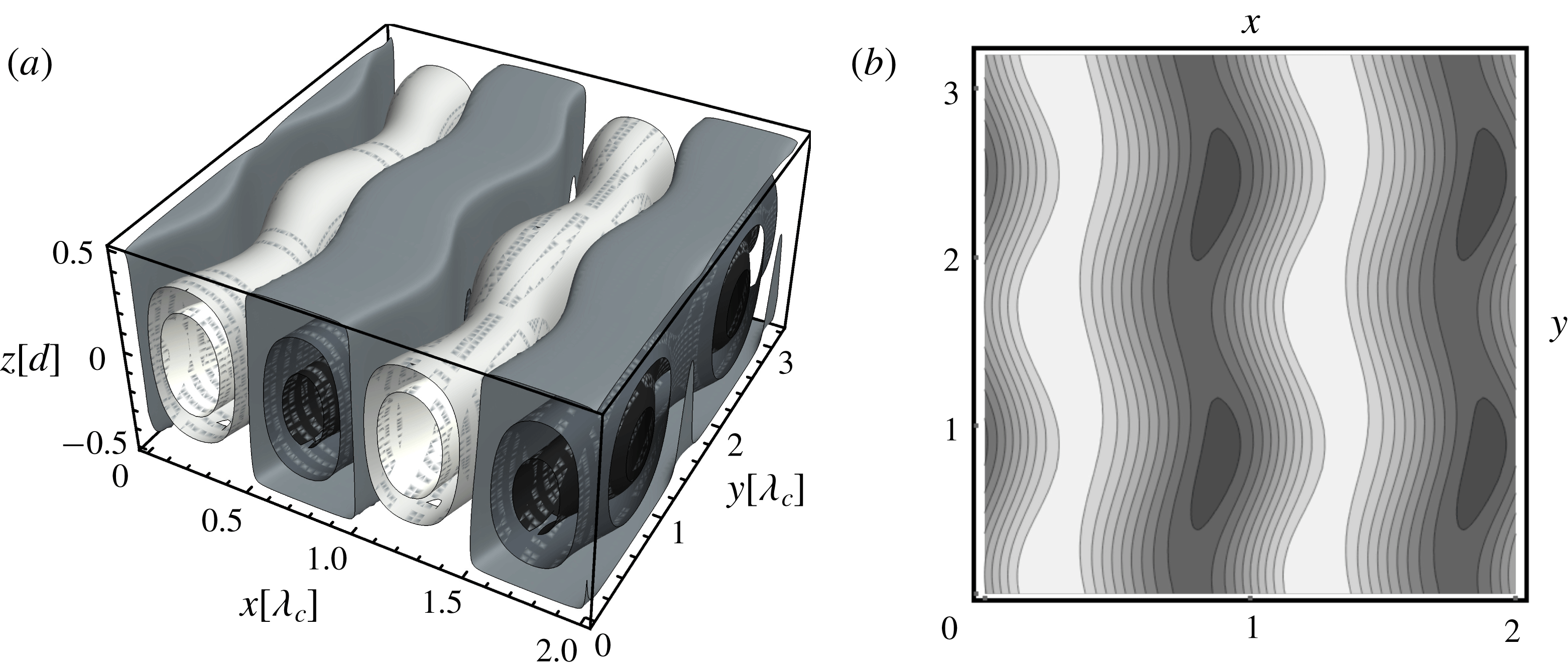
Figure 10. DNS for
![]() $\unicode[STIX]{x1D6FE}=6^{\circ }$
,
$\unicode[STIX]{x1D6FE}=6^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.07$
,
$\unicode[STIX]{x1D716}=0.07$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.33836$
,
$\unicode[STIX]{x1D716}_{0}=-0.33836$
,
![]() $\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2.175d$
with the periodicity lengths
$\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2.175d$
with the periodicity lengths
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{x}$
: (a) snapshot of a 3-D contour plot of the temperature
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{x}$
: (a) snapshot of a 3-D contour plot of the temperature
![]() $\unicode[STIX]{x1D703}(x,y,z)$
for
$\unicode[STIX]{x1D703}(x,y,z)$
for
![]() $0\leqq x\leqq 2\unicode[STIX]{x1D706}_{x}$
,
$0\leqq x\leqq 2\unicode[STIX]{x1D706}_{x}$
,
![]() $0\leqq y\leqq 2\unicode[STIX]{x1D706}_{y}=2(8/5)\unicode[STIX]{x1D706}_{c}$
and
$0\leqq y\leqq 2\unicode[STIX]{x1D706}_{y}=2(8/5)\unicode[STIX]{x1D706}_{c}$
and
![]() $-d/2<z<d/2$
; (b) 2-D contour plot of
$-d/2<z<d/2$
; (b) 2-D contour plot of
![]() $\unicode[STIX]{x1D703}(x,y,z)$
obtained from panel (a) for
$\unicode[STIX]{x1D703}(x,y,z)$
obtained from panel (a) for
![]() $y=0$
.
$y=0$
.
In analogy to the discussion of the SH patterns before, it is very useful to approximate the midplane temperature field
![]() $\unicode[STIX]{x1D703}(x,y,z=0,t)$
by a function
$\unicode[STIX]{x1D703}(x,y,z=0,t)$
by a function
![]() $h(x,y,t)$
(see § B.2). That is based on the leading Fourier coefficients with the wave vectors
$h(x,y,t)$
(see § B.2). That is based on the leading Fourier coefficients with the wave vectors
![]() $\boldsymbol{q}_{1}=(q_{c},0)$
,
$\boldsymbol{q}_{1}=(q_{c},0)$
,
![]() $\boldsymbol{q}_{2,3}=(q_{c},\pm s_{y})$
describing the basic transverse rolls (
$\boldsymbol{q}_{2,3}=(q_{c},\pm s_{y})$
describing the basic transverse rolls (
![]() $\boldsymbol{q}_{1}$
) and their destabilizing oscillatory modes (
$\boldsymbol{q}_{1}$
) and their destabilizing oscillatory modes (
![]() $\boldsymbol{q}_{2,3}$
). In addition the Fourier coefficient with wave vector
$\boldsymbol{q}_{2,3}$
). In addition the Fourier coefficient with wave vector
![]() $\boldsymbol{q}_{4}=(0,s_{y})$
is also of interest. Exploiting certain relations between the phases of these Fourier coefficients (see § B.2) one arrives finally at
$\boldsymbol{q}_{4}=(0,s_{y})$
is also of interest. Exploiting certain relations between the phases of these Fourier coefficients (see § B.2) one arrives finally at
with the phase velocity
![]() $v_{phas}=\unicode[STIX]{x1D714}/s_{y}$
. The amplitudes
$v_{phas}=\unicode[STIX]{x1D714}/s_{y}$
. The amplitudes
![]() $A_{0},B_{0},D_{0}$
obtained in our various DNS with different
$A_{0},B_{0},D_{0}$
obtained in our various DNS with different
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D716}$
are listed in table 3; in addition one finds there the frequency
$\unicode[STIX]{x1D716}$
are listed in table 3; in addition one finds there the frequency
![]() $\unicode[STIX]{x1D714}$
of the travelling waves together with the corresponding
$\unicode[STIX]{x1D714}$
of the travelling waves together with the corresponding
![]() $\unicode[STIX]{x1D714}_{0}$
at the onset of the OS-instability (see table 2). The amplitude
$\unicode[STIX]{x1D714}_{0}$
at the onset of the OS-instability (see table 2). The amplitude
![]() $D_{0}$
, always considerably smaller than
$D_{0}$
, always considerably smaller than
![]() $A_{0},B_{0}$
, vanishes for
$A_{0},B_{0}$
, vanishes for
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
and describes a
$\unicode[STIX]{x1D6FE}=0^{\circ }$
and describes a
![]() $x$
-independent contribution to
$x$
-independent contribution to
![]() $h(x,y,t)$
which is, however, practically not visible in DNS snapshots. Inspection of (3.2) shows that
$h(x,y,t)$
which is, however, practically not visible in DNS snapshots. Inspection of (3.2) shows that
![]() $D_{0}$
lifts the reflection symmetry
$D_{0}$
lifts the reflection symmetry
![]() $y\rightarrow -y$
in the comoving frame (
$y\rightarrow -y$
in the comoving frame (
![]() $v_{phas}=0$
) due to the constant positive phase shift
$v_{phas}=0$
) due to the constant positive phase shift
![]() $\unicode[STIX]{x1D713}_{C}=\unicode[STIX]{x03C0}/4(1+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}_{C})$
with a positive
$\unicode[STIX]{x1D713}_{C}=\unicode[STIX]{x03C0}/4(1+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}_{C})$
with a positive
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}<0.05$
. The representation of the downwards travelling waves is obtained from (3.2) by the transformations
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}<0.05$
. The representation of the downwards travelling waves is obtained from (3.2) by the transformations
![]() $v_{phas}\rightarrow -v_{phas}$
and
$v_{phas}\rightarrow -v_{phas}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}_{C}\rightarrow -\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}_{c}$
.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}_{C}\rightarrow -\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D713}_{c}$
.
Oscillatory standing-wave patterns appear typically when starting our DNS using restricted initial conditions (see appendix A). A representative time sequence is shown in figure 13, where the sidewise distortion amplitude of the rolls varies in time periodically between a maximum and a minimum. The corresponding function
![]() $h(x,y,t)$
for standing waves (see appendix B) reads as follows:
$h(x,y,t)$
for standing waves (see appendix B) reads as follows:

Figure 13. Time evolution of standing waves over one time period
![]() $T=16.0t_{v}$
, i.e. with
$T=16.0t_{v}$
, i.e. with
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/T=0.39237$
again for
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}/T=0.39237$
again for
![]() $\unicode[STIX]{x1D6FE}=6^{\circ }$
,
$\unicode[STIX]{x1D6FE}=6^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.07$
,
$\unicode[STIX]{x1D716}=0.07$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.33836$
.
$\unicode[STIX]{x1D716}_{0}=-0.33836$
.
In the planar case,
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
, we have compared our DNS with a previous one in the literature (Meneguzzi et al.
Reference Meneguzzi, Sulem, Sulem and Thual1987), which was performed for a small-aspect-ratio system (!) at
$\unicode[STIX]{x1D6FE}=0^{\circ }$
, we have compared our DNS with a previous one in the literature (Meneguzzi et al.
Reference Meneguzzi, Sulem, Sulem and Thual1987), which was performed for a small-aspect-ratio system (!) at
![]() $\unicode[STIX]{x1D716}=0.127$
, where
$\unicode[STIX]{x1D716}=0.127$
, where
![]() $L_{x}=\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x03C0}/q_{c}=2.016$
and
$L_{x}=\unicode[STIX]{x1D706}_{c}=2\unicode[STIX]{x03C0}/q_{c}=2.016$
and
![]() $L_{y}=2\unicode[STIX]{x03C0}/s_{y}=2.79$
for
$L_{y}=2\unicode[STIX]{x03C0}/s_{y}=2.79$
for
![]() $s_{y}=2.5$
. According to figure 10 in this paper the frequency of the resulting standing wave was approximately
$s_{y}=2.5$
. According to figure 10 in this paper the frequency of the resulting standing wave was approximately
![]() $\unicode[STIX]{x1D714}=1.6$
. For comparison we have performed a DNS with restricted initial conditions using a larger aspect ratio with
$\unicode[STIX]{x1D714}=1.6$
. For comparison we have performed a DNS with restricted initial conditions using a larger aspect ratio with
![]() $L_{x}=8\unicode[STIX]{x1D706}_{c}$
and
$L_{x}=8\unicode[STIX]{x1D706}_{c}$
and
![]() $L_{y}=6(2\unicode[STIX]{x03C0}/s_{y})=0.935L_{x}$
and also obtained
$L_{y}=6(2\unicode[STIX]{x03C0}/s_{y})=0.935L_{x}$
and also obtained
![]() $\unicode[STIX]{x1D714}=1.6$
, which is, however, larger than
$\unicode[STIX]{x1D714}=1.6$
, which is, however, larger than
![]() $\unicode[STIX]{x1D714}_{0}(\unicode[STIX]{x1D6FE}=0^{\circ })=1.394$
in table 2. However, this pattern was not stable, when continuing the DNS after superimposing arbitrary noise. We arrived at a travelling-wave pattern with a much smaller
$\unicode[STIX]{x1D714}_{0}(\unicode[STIX]{x1D6FE}=0^{\circ })=1.394$
in table 2. However, this pattern was not stable, when continuing the DNS after superimposing arbitrary noise. We arrived at a travelling-wave pattern with a much smaller
![]() $s_{y}=2.083$
, which compares well with
$s_{y}=2.083$
, which compares well with
![]() $s_{y}^{\mathit{OS}}=2.172$
. Also the frequency
$s_{y}^{\mathit{OS}}=2.172$
. Also the frequency
![]() $\unicode[STIX]{x1D714}=1.35$
fits much better
$\unicode[STIX]{x1D714}=1.35$
fits much better
![]() $\unicode[STIX]{x1D714}_{0}(s_{y})=1.394$
.
$\unicode[STIX]{x1D714}_{0}(s_{y})=1.394$
.
Note, that in the literature for
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
also the less realistic free-slip boundary conditions with respect to the velocity field have been applied (see e.g. Mishra, Wahi & Verma Reference Mishra, Wahi and Verma2010; Dan et al.
Reference Dan, Ghosh, Nandukumar, Dana and Pal2017). Though in this way the numerics is considerably simplified, one should be aware of profound qualitative differences to rigid boundary conditions in particular with respect to the vertical vorticity (Clever & Busse Reference Clever and Busse1974).
$\unicode[STIX]{x1D6FE}=0^{\circ }$
also the less realistic free-slip boundary conditions with respect to the velocity field have been applied (see e.g. Mishra, Wahi & Verma Reference Mishra, Wahi and Verma2010; Dan et al.
Reference Dan, Ghosh, Nandukumar, Dana and Pal2017). Though in this way the numerics is considerably simplified, one should be aware of profound qualitative differences to rigid boundary conditions in particular with respect to the vertical vorticity (Clever & Busse Reference Clever and Busse1974).
The following § 4 is devoted to some complex patterns to be found near the codimension-2 points or at larger
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
4 DNS of complex patterns
In the previous section we have described the OS and the SH patterns for
![]() $\unicode[STIX]{x1D6FE}$
away from the codimension-2 points. In their vicinity the patterns should show a tendency to become more complex, as indeed demonstrated in § 4.1 on the basis of some characteristic examples. In addition we expect more complicated patterns at larger
$\unicode[STIX]{x1D6FE}$
away from the codimension-2 points. In their vicinity the patterns should show a tendency to become more complex, as indeed demonstrated in § 4.1 on the basis of some characteristic examples. In addition we expect more complicated patterns at larger
![]() $\unicode[STIX]{x1D716}$
, which is confirmed in § 4.2.
$\unicode[STIX]{x1D716}$
, which is confirmed in § 4.2.
4.1 Patterns in the vicinity of the codimension-2 points
According to figure 3 and table 2 the first codimension-2 point appears at
![]() $\unicode[STIX]{x1D6FE}_{1}=1.023^{\circ }$
with
$\unicode[STIX]{x1D6FE}_{1}=1.023^{\circ }$
with
![]() $\unicode[STIX]{x1D716}_{\mathit{OS}}=\unicode[STIX]{x1D716}_{SH}=0.133$
, where
$\unicode[STIX]{x1D716}_{\mathit{OS}}=\unicode[STIX]{x1D716}_{SH}=0.133$
, where
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{1})=2.083$
. However, our DNS at a larger
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{1})=2.083$
. However, our DNS at a larger
![]() $\unicode[STIX]{x1D716}=0.14$
for
$\unicode[STIX]{x1D716}=0.14$
for
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{1})$
have always produced travelling waves with wavelengths
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{1})$
have always produced travelling waves with wavelengths
![]() $\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}$
and
$\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}$
and
![]() $\unicode[STIX]{x1D706}_{y}=L_{y}/5=3.237$
where
$\unicode[STIX]{x1D706}_{y}=L_{y}/5=3.237$
where
![]() $s_{y}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{y}=1.94$
differs not too much from
$s_{y}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{y}=1.94$
differs not too much from
![]() $s_{y}^{\mathit{OS}}=2.070$
. In contrast, the frequency
$s_{y}^{\mathit{OS}}=2.070$
. In contrast, the frequency
![]() $\unicode[STIX]{x1D714}=1.26$
is not well approximated by
$\unicode[STIX]{x1D714}=1.26$
is not well approximated by
![]() $\unicode[STIX]{x1D714}_{0}=1.314$
. There was no trace of the competing SH instability, maybe because
$\unicode[STIX]{x1D714}_{0}=1.314$
. There was no trace of the competing SH instability, maybe because
![]() $s_{y}^{SH}=1.672$
deviates too much from
$s_{y}^{SH}=1.672$
deviates too much from
![]() $s_{y}^{\mathit{OS}}$
. These general features remain robust, when increasing the horizontal size of the system to
$s_{y}^{\mathit{OS}}$
. These general features remain robust, when increasing the horizontal size of the system to
![]() $L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{1})$
using
$L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{1})$
using
![]() $256\times 256$
Fourier modes in the
$256\times 256$
Fourier modes in the
![]() $x{-}y$
plane. The system produces again an OS pattern with
$x{-}y$
plane. The system produces again an OS pattern with
![]() $\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}$
but a smaller
$\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}$
but a smaller
![]() $\unicode[STIX]{x1D706}_{y}=L_{y}/11=2.843$
where
$\unicode[STIX]{x1D706}_{y}=L_{y}/11=2.843$
where
![]() $s_{y}=2.14>s_{y}^{\mathit{OS}}$
. The frequency
$s_{y}=2.14>s_{y}^{\mathit{OS}}$
. The frequency
![]() $\unicode[STIX]{x1D714}=1.35$
was now larger than
$\unicode[STIX]{x1D714}=1.35$
was now larger than
![]() $\unicode[STIX]{x1D714}_{0}$
.
$\unicode[STIX]{x1D714}_{0}$
.
An analogous scenario was observed at the codimension-2 point
![]() $\unicode[STIX]{x1D6FE}_{2}=2.183^{\circ }$
where
$\unicode[STIX]{x1D6FE}_{2}=2.183^{\circ }$
where
![]() $\unicode[STIX]{x1D716}_{SH}=\unicode[STIX]{x1D716}_{\mathit{OS}}=0.117$
(see table 2) and
$\unicode[STIX]{x1D716}_{SH}=\unicode[STIX]{x1D716}_{\mathit{OS}}=0.117$
(see table 2) and
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})=2.044$
. Here the DNS have always produced at
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})=2.044$
. Here the DNS have always produced at
![]() $\unicode[STIX]{x1D716}=0.125$
with
$\unicode[STIX]{x1D716}=0.125$
with
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})$
perfect SH patterns without any trace of OS motifs. The DNS have locked into
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})$
perfect SH patterns without any trace of OS motifs. The DNS have locked into
![]() $\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})_{2}=2.043$
and
$\unicode[STIX]{x1D706}_{x}=\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})_{2}=2.043$
and
![]() $\unicode[STIX]{x1D706}_{y}=(8/6)\unicode[STIX]{x1D706}_{x}$
, which corresponds to
$\unicode[STIX]{x1D706}_{y}=(8/6)\unicode[STIX]{x1D706}_{x}$
, which corresponds to
![]() $s_{y}=2.306$
considerably different from
$s_{y}=2.306$
considerably different from
![]() $s_{y}^{SH}=2.468$
. For larger
$s_{y}^{SH}=2.468$
. For larger
![]() $L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})$
and again with
$L_{x}=L_{y}=16\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})$
and again with
![]() $\unicode[STIX]{x1D716}=0.125$
the DNS had more freedom and locked into
$\unicode[STIX]{x1D716}=0.125$
the DNS had more freedom and locked into
![]() $\unicode[STIX]{x1D706}_{y}=16/13\unicode[STIX]{x1D706}_{c}$
corresponding to
$\unicode[STIX]{x1D706}_{y}=16/13\unicode[STIX]{x1D706}_{c}$
corresponding to
![]() $s_{y}=2.496$
much nearer to
$s_{y}=2.496$
much nearer to
![]() $s_{y}^{SH}$
. The fact that
$s_{y}^{SH}$
. The fact that
![]() $s_{y}^{\mathit{OS}}=1.898$
is considerably smaller than the
$s_{y}^{\mathit{OS}}=1.898$
is considerably smaller than the
![]() $s_{y}$
values selected in the DNS, might explain why the competing OS instability has played no role.
$s_{y}$
values selected in the DNS, might explain why the competing OS instability has played no role.

Figure 14. Heteroclinic cycle with subharmonic, transverse and oblique patterns from a DNS at
![]() $\unicode[STIX]{x1D6FE}=1.5^{\circ }$
with
$\unicode[STIX]{x1D6FE}=1.5^{\circ }$
with
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
at
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
at
![]() $\unicode[STIX]{x1D716}=0.165$
(
$\unicode[STIX]{x1D716}=0.165$
(
![]() $\unicode[STIX]{x1D716}_{0}=0.0945$
). The pictures are sorted with increasing time
$\unicode[STIX]{x1D716}_{0}=0.0945$
). The pictures are sorted with increasing time
![]() $t$
from left to right and top to bottom and correspond to
$t$
from left to right and top to bottom and correspond to
![]() $t=0$
(a), 68 (b), 195 (c), 278 (d), 702 (e), 755 (f), 788 (g), 873 (h) in units of
$t=0$
(a), 68 (b), 195 (c), 278 (d), 702 (e), 755 (f), 788 (g), 873 (h) in units of
![]() $t_{v}$
.
$t_{v}$
.
Inspection of table 2 shows immediately that
![]() $s_{y}^{\mathit{OS}}$
monotonically decreases with
$s_{y}^{\mathit{OS}}$
monotonically decreases with
![]() $\unicode[STIX]{x1D6FE}$
while
$\unicode[STIX]{x1D6FE}$
while
![]() $s_{y}^{SH}$
increases as long
$s_{y}^{SH}$
increases as long
![]() $\unicode[STIX]{x1D6FE}<5^{\circ }$
. Thus there was the chance that in a DNS for
$\unicode[STIX]{x1D6FE}<5^{\circ }$
. Thus there was the chance that in a DNS for
![]() $\unicode[STIX]{x1D6FE}$
between
$\unicode[STIX]{x1D6FE}$
between
![]() $\unicode[STIX]{x1D6FE}_{1}$
and
$\unicode[STIX]{x1D6FE}_{1}$
and
![]() $\unicode[STIX]{x1D6FE}_{2}$
both stationary SH- and oscillatory motifs might appear. That was indeed the case: in a DNS at
$\unicode[STIX]{x1D6FE}_{2}$
both stationary SH- and oscillatory motifs might appear. That was indeed the case: in a DNS at
![]() $\unicode[STIX]{x1D6FE}=1.5^{\circ }$
for
$\unicode[STIX]{x1D6FE}=1.5^{\circ }$
for
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})$
with
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})$
with
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})=2.03$
and for
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{2})=2.03$
and for
![]() $\unicode[STIX]{x1D716}=0.165$
slightly larger than the
$\unicode[STIX]{x1D716}=0.165$
slightly larger than the
![]() $\unicode[STIX]{x1D716}_{in}$
of both the SH and OS instabilities we found a persistent heteroclinic cycle as shown in figure 14. One starts with a transverse roll pattern with 8 roll pairs, which first transforms into a SH pattern. Later we find a pattern with 7 oblique roll pairs which first become transverse, before the original 8 roll pair pattern is recovered. This scheme repeats itself every
$\unicode[STIX]{x1D716}_{in}$
of both the SH and OS instabilities we found a persistent heteroclinic cycle as shown in figure 14. One starts with a transverse roll pattern with 8 roll pairs, which first transforms into a SH pattern. Later we find a pattern with 7 oblique roll pairs which first become transverse, before the original 8 roll pair pattern is recovered. This scheme repeats itself every
![]() $873t_{v}$
. We concentrate on SH-type pictures in figure 14 and the corresponding Fourier modes with wave vectors
$873t_{v}$
. We concentrate on SH-type pictures in figure 14 and the corresponding Fourier modes with wave vectors
![]() $\boldsymbol{q}_{1,2,3}$
which describe, according to (3.1), a SH pattern. Thus generalizing the representation of stationary SH patterns in (3.1) (see also § B.1) we use the time-dependent amplitudes
$\boldsymbol{q}_{1,2,3}$
which describe, according to (3.1), a SH pattern. Thus generalizing the representation of stationary SH patterns in (3.1) (see also § B.1) we use the time-dependent amplitudes
![]() $A_{0}(t),B_{0}(t)$
shown in figure 15 to describe the SH motifs in figure 14. The times
$A_{0}(t),B_{0}(t)$
shown in figure 15 to describe the SH motifs in figure 14. The times
![]() $t$
, at which the pictures are presented in figure 14, are marked with the black bullets on the time axis of the figure 15. For the perfect transverse roll pattern at
$t$
, at which the pictures are presented in figure 14, are marked with the black bullets on the time axis of the figure 15. For the perfect transverse roll pattern at
![]() $t=0$
the amplitude
$t=0$
the amplitude
![]() $A_{0}$
is maximal, while
$A_{0}$
is maximal, while
![]() $B_{0}=0$
. Then
$B_{0}=0$
. Then
![]() $A_{0}$
decreases and
$A_{0}$
decreases and
![]() $B_{0}$
grows for the following SH pattern. Afterwards both
$B_{0}$
grows for the following SH pattern. Afterwards both
![]() $A_{0},B_{0}$
essentially become zero for the oblique roll patterns, before the transverse rolls appear again. It took approximately
$A_{0},B_{0}$
essentially become zero for the oblique roll patterns, before the transverse rolls appear again. It took approximately
![]() $10\,000t_{v}$
for the cycle to become stable and we followed it over 15 cycles in our simulation.
$10\,000t_{v}$
for the cycle to become stable and we followed it over 15 cycles in our simulation.
Finally, we address the codimension-2 point at
![]() $\unicode[STIX]{x1D6FE}_{3}=6.169^{\circ }$
for
$\unicode[STIX]{x1D6FE}_{3}=6.169^{\circ }$
for
![]() $\unicode[STIX]{x1D716}=0.051$
, where a SH instability with
$\unicode[STIX]{x1D716}=0.051$
, where a SH instability with
![]() $s_{y}=1.62$
competes with an OS instability with
$s_{y}=1.62$
competes with an OS instability with
![]() $s_{y}=1.92$
. A simulation with
$s_{y}=1.92$
. A simulation with
![]() $\unicode[STIX]{x1D716}=0.08$
led to a weakly chaotic sequence of patterns, which are shown in figure 16. It took approximately
$\unicode[STIX]{x1D716}=0.08$
led to a weakly chaotic sequence of patterns, which are shown in figure 16. It took approximately
![]() $10\,000t_{v}$
in our DNS before that characteristic pattern sequence appeared for the first time, which then persisted afterwards. However, the time lapse between the reappearance of the transverse roll pattern was not constant and varied between
$10\,000t_{v}$
in our DNS before that characteristic pattern sequence appeared for the first time, which then persisted afterwards. However, the time lapse between the reappearance of the transverse roll pattern was not constant and varied between
![]() $1000t_{v}$
and
$1000t_{v}$
and
![]() $1600t_{v}$
.
$1600t_{v}$
.

Figure 16. Heteroclinic orbit between OS, SH and transverse roll patterns for
![]() $\unicode[STIX]{x1D6FE}=6.169^{\circ }$
,
$\unicode[STIX]{x1D6FE}=6.169^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.08$
and
$\unicode[STIX]{x1D716}=0.08$
and
![]() $\unicode[STIX]{x1D716}_{0}=-0.3419$
with
$\unicode[STIX]{x1D716}_{0}=-0.3419$
with
![]() $L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. The snapshots of
$L_{x}=L_{y}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
. The snapshots of
![]() $h(x,y,t)$
are shown at times
$h(x,y,t)$
are shown at times
![]() $t=0$
(a), 140 (b), 690 (c), 890 (d), 1130 (e), 1300 (f), 1360 (g), 1490 (h) in units of
$t=0$
(a), 140 (b), 690 (c), 890 (d), 1130 (e), 1300 (f), 1360 (g), 1490 (h) in units of
![]() $t_{v}$
increasing from left to right and from top to bottom.
$t_{v}$
increasing from left to right and from top to bottom.

Figure 17. Domain chaos in a system with
![]() $L_{x}=L_{y}=20\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
and the same parameters as in figure 16 (
$L_{x}=L_{y}=20\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
and the same parameters as in figure 16 (
![]() $\unicode[STIX]{x1D6FE}=6.169^{\circ }$
,
$\unicode[STIX]{x1D6FE}=6.169^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.08$
). Snapshots of the midplane temperature from a DNS started with random initial conditions at consecutive times
$\unicode[STIX]{x1D716}=0.08$
). Snapshots of the midplane temperature from a DNS started with random initial conditions at consecutive times
![]() $t=3080$
(a), 3948 (b) and
$t=3080$
(a), 3948 (b) and
![]() $4198t_{v}$
(c).
$4198t_{v}$
(c).
However, for the larger aspect ratio
![]() $L_{x}=L_{y}=20\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{3})$
with otherwise the same parameters as before, we observed a different scenario. One finds a kind of domain chaos as exemplified by the three snapshots in figure 17 taken at increasing times. The pictures show a background of transverse rolls superseded by SH patches and some dislocations, whose locations change with time.
$L_{x}=L_{y}=20\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE}_{3})$
with otherwise the same parameters as before, we observed a different scenario. One finds a kind of domain chaos as exemplified by the three snapshots in figure 17 taken at increasing times. The pictures show a background of transverse rolls superseded by SH patches and some dislocations, whose locations change with time.
4.2 Complex patterns at larger
 $\unicode[STIX]{x1D716}$
$\unicode[STIX]{x1D716}$
In this section we discuss two very time-consuming simulations, to obtain a first impression of the pattern dynamics for larger
![]() $\unicode[STIX]{x1D716}$
. The first example deals with OS patterns for
$\unicode[STIX]{x1D716}$
. The first example deals with OS patterns for
![]() $\unicode[STIX]{x1D716}=0.172>\unicode[STIX]{x1D716}_{\mathit{OS}}=0.111$
and for
$\unicode[STIX]{x1D716}=0.172>\unicode[STIX]{x1D716}_{\mathit{OS}}=0.111$
and for
![]() $\unicode[STIX]{x1D6FE}=0.5^{\circ }$
, where the system is slightly anisotropic. The periodicity lengths have been chosen as
$\unicode[STIX]{x1D6FE}=0.5^{\circ }$
, where the system is slightly anisotropic. The periodicity lengths have been chosen as
![]() $L_{x}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
and
$L_{x}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
and
![]() $L_{y}=5\unicode[STIX]{x1D706}_{y}$
with
$L_{y}=5\unicode[STIX]{x1D706}_{y}$
with
![]() $\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2.018$
and
$\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})=2.018$
and
![]() $\unicode[STIX]{x1D706}_{y}=(2\unicode[STIX]{x03C0})/s_{y}$
where
$\unicode[STIX]{x1D706}_{y}=(2\unicode[STIX]{x03C0})/s_{y}$
where
![]() $s_{y}=s_{y}^{\mathit{OS}}=2.147$
. First, using restricted random initial conditions (see appendix A) a standing-wave pattern has been constructed, which was stable after
$s_{y}=s_{y}^{\mathit{OS}}=2.147$
. First, using restricted random initial conditions (see appendix A) a standing-wave pattern has been constructed, which was stable after
![]() $350t_{v}$
. It is perfectly described by (3.3) with the amplitudes
$350t_{v}$
. It is perfectly described by (3.3) with the amplitudes
![]() $A_{0}=71.4$
,
$A_{0}=71.4$
,
![]() $A_{1}=3.7$
,
$A_{1}=3.7$
,
![]() $B_{0}=52.4$
. The frequency
$B_{0}=52.4$
. The frequency
![]() $\unicode[STIX]{x1D714}=1.45$
was comparable with
$\unicode[STIX]{x1D714}=1.45$
was comparable with
![]() $\unicode[STIX]{x1D714}_{0}=1.376$
. Then we superimposed noise and continued the run. In figure 18 we show representative snapshots. Their inspection clearly demonstrates that, besides the basic modes
$\unicode[STIX]{x1D714}_{0}=1.376$
. Then we superimposed noise and continued the run. In figure 18 we show representative snapshots. Their inspection clearly demonstrates that, besides the basic modes
![]() $\boldsymbol{q}_{1,2,3}$
, additional modes come into play. Nevertheless the contribution of the basic modes is still well described by (3.2) except that we need time-dependent coefficients
$\boldsymbol{q}_{1,2,3}$
, additional modes come into play. Nevertheless the contribution of the basic modes is still well described by (3.2) except that we need time-dependent coefficients
![]() $A_{0}(t)$
,
$A_{0}(t)$
,
![]() $B_{0}(t)$
, which are presented in figure 19. They vary periodically in time with a period of approximately
$B_{0}(t)$
, which are presented in figure 19. They vary periodically in time with a period of approximately
![]() $123t_{v}$
much larger than the fast period
$123t_{v}$
much larger than the fast period
![]() $\unicode[STIX]{x1D70F}=(2\unicode[STIX]{x03C0})/\unicode[STIX]{x1D714}=3.9t_{v}$
, where
$\unicode[STIX]{x1D70F}=(2\unicode[STIX]{x03C0})/\unicode[STIX]{x1D714}=3.9t_{v}$
, where
![]() $\unicode[STIX]{x1D714}=1.62$
is now considerably larger than the value
$\unicode[STIX]{x1D714}=1.62$
is now considerably larger than the value
![]() $\unicode[STIX]{x1D714}=1.45$
for the standing waves above.
$\unicode[STIX]{x1D714}=1.45$
for the standing waves above.

Figure 18. Complex travelling-wave pattern for
![]() $\unicode[STIX]{x1D6FE}=0.5^{\circ }$
,
$\unicode[STIX]{x1D6FE}=0.5^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.172$
,
$\unicode[STIX]{x1D716}=0.172$
,
![]() $\unicode[STIX]{x1D716}_{0}=0.163$
,
$\unicode[STIX]{x1D716}_{0}=0.163$
,
![]() $L_{x}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
,
$L_{x}=8\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
,
![]() $L_{y}=0.906L_{x}$
. The pictures are sorted increasing in time from left to right at
$L_{y}=0.906L_{x}$
. The pictures are sorted increasing in time from left to right at
![]() $t=3728$
(a), 3741 (b), 3779 (c), 3804 (d), 3851 (e) in units of
$t=3728$
(a), 3741 (b), 3779 (c), 3804 (d), 3851 (e) in units of
![]() $t_{v}$
. For the travelling waves we find
$t_{v}$
. For the travelling waves we find
![]() $\unicode[STIX]{x1D714}=1.62$
.
$\unicode[STIX]{x1D714}=1.62$
.
Finally we consider a complex SH-pattern for
![]() $\unicode[STIX]{x1D6FE}=50^{\circ }$
and
$\unicode[STIX]{x1D6FE}=50^{\circ }$
and
![]() $\unicode[STIX]{x1D716}=0.15>\unicode[STIX]{x1D716}_{in}^{SH}=0.05$
. Here, according to figure 3(b), the transverse rolls are also linearly unstable against oscillatory modes. Inspection of figure 20 shows that these are indeed reflected in the transients of a DNS starting with general random noise. But finally we arrived at a slightly oblique stationary SH-pattern, which was stable.
$\unicode[STIX]{x1D716}=0.15>\unicode[STIX]{x1D716}_{in}^{SH}=0.05$
. Here, according to figure 3(b), the transverse rolls are also linearly unstable against oscillatory modes. Inspection of figure 20 shows that these are indeed reflected in the transients of a DNS starting with general random noise. But finally we arrived at a slightly oblique stationary SH-pattern, which was stable.

Figure 20. Oblique SH pattern for
![]() $\unicode[STIX]{x1D6FE}=50^{\circ }$
,
$\unicode[STIX]{x1D6FE}=50^{\circ }$
,
![]() $\unicode[STIX]{x1D716}=0.15$
,
$\unicode[STIX]{x1D716}=0.15$
,
![]() $\unicode[STIX]{x1D716}_{0}=-0.8410$
,
$\unicode[STIX]{x1D716}_{0}=-0.8410$
,
![]() $L_{x}=8\unicode[STIX]{x1D706}_{c}$
,
$L_{x}=8\unicode[STIX]{x1D706}_{c}$
,
![]() $L_{y}=1.087L_{x}$
. For the subharmonic pattern we find
$L_{y}=1.087L_{x}$
. For the subharmonic pattern we find
![]() $s_{y}=1.575$
. The simulations were started with random noise. The pictures are sorted increasing in time from left to right at
$s_{y}=1.575$
. The simulations were started with random noise. The pictures are sorted increasing in time from left to right at
![]() $t=120$
(a), 440 (b), 1800 (c), 2540 (d), 4800 (e) in units of
$t=120$
(a), 440 (b), 1800 (c), 2540 (d), 4800 (e) in units of
![]() $t_{v}$
.
$t_{v}$
.
5 Concluding remarks
In this paper we have presented a theoretical analysis of ILC for a low-Prandtl-number fluid (mercury,
![]() $Pr=0.025$
), where the fluid layer includes an angle (
$Pr=0.025$
), where the fluid layer includes an angle (
![]() $90^{\circ }+\unicode[STIX]{x1D6FE}$
) with the gravity vector
$90^{\circ }+\unicode[STIX]{x1D6FE}$
) with the gravity vector
![]() $\boldsymbol{g}$
(see figure 1). The focus has been on large-aspect-ratio systems with Rayleigh numbers
$\boldsymbol{g}$
(see figure 1). The focus has been on large-aspect-ratio systems with Rayleigh numbers
![]() $R$
slightly above the critical values
$R$
slightly above the critical values
![]() $R_{c}(\unicode[STIX]{x1D6FE})$
in the spirit of a previous study of ILC with
$R_{c}(\unicode[STIX]{x1D6FE})$
in the spirit of a previous study of ILC with
![]() $Pr=1.07$
(Subramanian et al.
Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016), where an excellent agreement with the corresponding experiments has been achieved. In close analogy to that paper our calculations are based on a bifurcation approach to determine the critical data
$Pr=1.07$
(Subramanian et al.
Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016), where an excellent agreement with the corresponding experiments has been achieved. In close analogy to that paper our calculations are based on a bifurcation approach to determine the critical data
![]() $R_{c},\boldsymbol{q}_{c}$
and the secondary instabilities of the primary roll patterns. In addition DNS have been used to characterize the pattern evolution.
$R_{c},\boldsymbol{q}_{c}$
and the secondary instabilities of the primary roll patterns. In addition DNS have been used to characterize the pattern evolution.
Inclining the fluid layer breaks isotropy and convection rolls with a definite orientation are seeded at
![]() $R=R_{c}$
. For instance, the uniform roll patterns produced at small
$R=R_{c}$
. For instance, the uniform roll patterns produced at small
![]() $\unicode[STIX]{x1D6FE}$
have been used to provide the appropriate initial conditions for experiments at
$\unicode[STIX]{x1D6FE}$
have been used to provide the appropriate initial conditions for experiments at
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
. This procedure has been shown to be crucial to match the stability diagram of standard, non-inclined RBC with experiments for
$\unicode[STIX]{x1D6FE}=0^{\circ }$
. This procedure has been shown to be crucial to match the stability diagram of standard, non-inclined RBC with experiments for
![]() $Pr\sim 1$
(Cakmur et al.
Reference Cakmur, Egolf, Plapp and Bodenschatz1997).
$Pr\sim 1$
(Cakmur et al.
Reference Cakmur, Egolf, Plapp and Bodenschatz1997).
In general, the pattern types bifurcating at onset and their secondary instabilities vary with
![]() $\unicode[STIX]{x1D6FE}$
. For not too small
$\unicode[STIX]{x1D6FE}$
. For not too small
![]() $Pr>0.264$
(see e.g. Subramanian et al.
Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) there exists a codimension-2 angle,
$Pr>0.264$
(see e.g. Subramanian et al.
Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016) there exists a codimension-2 angle,
![]() $\unicode[STIX]{x1D6FE}_{c2}$
. It separates the regime of longitudinal roll patterns at onset with their axes parallel to the incline from the regime of transverse ones with perpendicular orientation. In particular for
$\unicode[STIX]{x1D6FE}_{c2}$
. It separates the regime of longitudinal roll patterns at onset with their axes parallel to the incline from the regime of transverse ones with perpendicular orientation. In particular for
![]() $\unicode[STIX]{x1D6FE}\approx \unicode[STIX]{x1D6FE}_{c2}$
one observes then complex patterns in experiments in agreement with the theory.
$\unicode[STIX]{x1D6FE}\approx \unicode[STIX]{x1D6FE}_{c2}$
one observes then complex patterns in experiments in agreement with the theory.
Convection in low-Prandtl-number fluids for
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
and
$\unicode[STIX]{x1D6FE}=0^{\circ }$
and
![]() $R\gtrsim R_{c}$
has also attracted considerable interest in the past (see e.g. Rossby Reference Rossby1969; Libchaber, Laroche & Fauve Reference Libchaber, Laroche and Fauve1982; Meneguzzi et al.
Reference Meneguzzi, Sulem, Sulem and Thual1987; Clever & Busse Reference Clever and Busse1990; Thual Reference Thual1992). Here the primary bifurcation is always to transverse rolls for arbitrary
$R\gtrsim R_{c}$
has also attracted considerable interest in the past (see e.g. Rossby Reference Rossby1969; Libchaber, Laroche & Fauve Reference Libchaber, Laroche and Fauve1982; Meneguzzi et al.
Reference Meneguzzi, Sulem, Sulem and Thual1987; Clever & Busse Reference Clever and Busse1990; Thual Reference Thual1992). Here the primary bifurcation is always to transverse rolls for arbitrary
![]() $\unicode[STIX]{x1D6FE}$
. However, an oscillatory secondary bifurcation, leading to travelling waves appears already very close to
$\unicode[STIX]{x1D6FE}$
. However, an oscillatory secondary bifurcation, leading to travelling waves appears already very close to
![]() $R_{c}$
, which has in particular motivated the theoretical studies. It seemed thus natural to investigate low-Prandtl-number ILC for finite
$R_{c}$
, which has in particular motivated the theoretical studies. It seemed thus natural to investigate low-Prandtl-number ILC for finite
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.
In general, the resulting patterns turned out to be more complex than anticipated. For instance, the secondary bifurcation of the transverse rolls leads either to OS travelling-wave patterns or to 3-D stationary SH ones, which alternate three times with each other already in the fairly small interval
![]() $0^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 6^{\circ }$
. This explains the appearance of complex patterns near the corresponding three codimension-2 points in § 4. In the spirit of an amplitude-equation approach the SH and OS patterns are described by only three leading Fourier modes with a characteristic relation between their phases (see § 3).
$0^{\circ }\leqslant \unicode[STIX]{x1D6FE}\leqslant 6^{\circ }$
. This explains the appearance of complex patterns near the corresponding three codimension-2 points in § 4. In the spirit of an amplitude-equation approach the SH and OS patterns are described by only three leading Fourier modes with a characteristic relation between their phases (see § 3).
For completeness it should be mentioned that a strong sensitivity of the bifurcations at small
![]() $\unicode[STIX]{x1D6FE}$
and small
$\unicode[STIX]{x1D6FE}$
and small
![]() $R\gtrsim R_{c}$
has been also described recently in a theoretical analysis of ILC in binary fluids (Mercader et al.
Reference Mercader, Batiste, Alonso and Knobloch2019). However, this system qualitatively differs from ours: the primary bifurcation of the basic state is typically not continuous and leads to travelling waves already at
$R\gtrsim R_{c}$
has been also described recently in a theoretical analysis of ILC in binary fluids (Mercader et al.
Reference Mercader, Batiste, Alonso and Knobloch2019). However, this system qualitatively differs from ours: the primary bifurcation of the basic state is typically not continuous and leads to travelling waves already at
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
at
$\unicode[STIX]{x1D6FE}=0^{\circ }$
at
![]() $R=R_{c}$
. Depending on
$R=R_{c}$
. Depending on
![]() $\unicode[STIX]{x1D6FE}$
a whole zoo of different pattern types develops, which often are in particular confined to a small part of the fluid layer.
$\unicode[STIX]{x1D6FE}$
a whole zoo of different pattern types develops, which often are in particular confined to a small part of the fluid layer.
Already decades ago it has also been demonstrated in convection experiments with mercury (Libchaber et al.
Reference Libchaber, Laroche and Fauve1982) for
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
, that an additional magnetic field applied parallel to the fluid layer has an important impact. This has been confirmed in many theoretical studies (see e.g. Busse & Clever Reference Busse and Clever1989) and also continuously extended to the turbulent regime (see e.g. Vogt et al. (Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018) and references therein). In general, the magnetic field leads to a preferred orientation of the roll axes parallel to the magnetic field. Thus for instance a magnetic field along the incline exerts a kind of torque on the standard transverse rolls for
$\unicode[STIX]{x1D6FE}=0^{\circ }$
, that an additional magnetic field applied parallel to the fluid layer has an important impact. This has been confirmed in many theoretical studies (see e.g. Busse & Clever Reference Busse and Clever1989) and also continuously extended to the turbulent regime (see e.g. Vogt et al. (Reference Vogt, Ishimi, Yanagisawa, Tasaka, Sakuraba and Eckert2018) and references therein). In general, the magnetic field leads to a preferred orientation of the roll axes parallel to the magnetic field. Thus for instance a magnetic field along the incline exerts a kind of torque on the standard transverse rolls for
![]() $\unicode[STIX]{x1D6FE}\neq 0^{\circ }$
and small
$\unicode[STIX]{x1D6FE}\neq 0^{\circ }$
and small
![]() $Pr$
. Thus one expects novel complex convection patterns and their secondary bifurcations in this case already near onset, which we plan to investigate in the near future.
$Pr$
. Thus one expects novel complex convection patterns and their secondary bifurcations in this case already near onset, which we plan to investigate in the near future.
Acknowledgements
The authors are grateful to Professor F. Busse for many valuable discussions and to Professor J. Schumacher for his hints on the most recent publications on low-Prandtl-number convection.
Appendix A. On the time integration of the OBE
The DNS in this paper is based on a pseudo-spectral code already used in Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). Thus according to (2.9) the simulations run in Fourier space on a discrete set of
![]() $N^{2}$
wave vectors
$N^{2}$
wave vectors
![]() $\boldsymbol{q}=(k\unicode[STIX]{x0394}q_{x},l\unicode[STIX]{x0394}q_{y})$
with
$\boldsymbol{q}=(k\unicode[STIX]{x0394}q_{x},l\unicode[STIX]{x0394}q_{y})$
with
![]() $-N/2\leqslant (k,l)\leqslant N/2-1$
. For the periodicity lengths in this paper we use typically
$-N/2\leqslant (k,l)\leqslant N/2-1$
. For the periodicity lengths in this paper we use typically
![]() $L_{x}=L_{y}=n\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
with
$L_{x}=L_{y}=n\unicode[STIX]{x1D706}_{c}(\unicode[STIX]{x1D6FE})$
with
![]() $n=8$
, 16, 20 and
$n=8$
, 16, 20 and
![]() $N=128$
, 256, 320, respectively. In some cases we allow for
$N=128$
, 256, 320, respectively. In some cases we allow for
![]() $L_{x}\neq L_{y}$
, which implies a corresponding small difference between
$L_{x}\neq L_{y}$
, which implies a corresponding small difference between
![]() $\unicode[STIX]{x0394}q_{x}$
and
$\unicode[STIX]{x0394}q_{x}$
and
![]() $\unicode[STIX]{x0394}q_{y}$
. In this way it is possible to produce periodic patterns with a prescribed wavelength
$\unicode[STIX]{x0394}q_{y}$
. In this way it is possible to produce periodic patterns with a prescribed wavelength
![]() $\unicode[STIX]{x1D706}_{y}$
that match in Fourier space the corresponding Galerkin Floquet vectors
$\unicode[STIX]{x1D706}_{y}$
that match in Fourier space the corresponding Galerkin Floquet vectors
![]() $\boldsymbol{s}$
with the
$\boldsymbol{s}$
with the
![]() $y$
-component
$y$
-component
![]() $s_{y}=(2\unicode[STIX]{x03C0})/\unicode[STIX]{x1D706}_{y}$
.
$s_{y}=(2\unicode[STIX]{x03C0})/\unicode[STIX]{x1D706}_{y}$
.
For the time integration we use an ‘exponential time-differencing method’ also described in appendix B1 of Subramanian et al. (Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016). We found in general time steps of
![]() $\text{d}t=0.002t_{v}$
to be sufficient to resolve the dynamics of the patterns and to guarantee robust results. In all cases we made sure that the secondary instabilities according to the Galerkin analysis are perfectly reproduced in our DNS. In view of typical transients of
$\text{d}t=0.002t_{v}$
to be sufficient to resolve the dynamics of the patterns and to guarantee robust results. In all cases we made sure that the secondary instabilities according to the Galerkin analysis are perfectly reproduced in our DNS. In view of typical transients of
![]() $1000t_{v}$
and more before the patterns would become steady (see e.g. § 3.2), our DNS are in general very time consuming. Using
$1000t_{v}$
and more before the patterns would become steady (see e.g. § 3.2), our DNS are in general very time consuming. Using
![]() $\unicode[STIX]{x1D705}=4.62\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
for mercury the thermal diffusivity time takes the value
$\unicode[STIX]{x1D705}=4.62\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
for mercury the thermal diffusivity time takes the value
![]() $t_{v}=d^{2}/\unicode[STIX]{x1D705}=21.6~\text{s}$
for
$t_{v}=d^{2}/\unicode[STIX]{x1D705}=21.6~\text{s}$
for
![]() $d=1~\text{cm}$
. Thus our DNS needed typically more than
$d=1~\text{cm}$
. Thus our DNS needed typically more than
![]() $5\times 10^{5}$
time steps in particular for the OS patterns.
$5\times 10^{5}$
time steps in particular for the OS patterns.
Note, that in view of the periodic boundary conditions, the origin of the coordinate system in the
![]() $x{-}y$
plane can be arbitrarily shifted, when analysing a single run. Thus a shift by
$x{-}y$
plane can be arbitrarily shifted, when analysing a single run. Thus a shift by
![]() $\boldsymbol{x}_{0}=(x_{0},y_{0})$
with arbitrary
$\boldsymbol{x}_{0}=(x_{0},y_{0})$
with arbitrary
![]() $x_{0},y_{0}$
leads to a phase factor
$x_{0},y_{0}$
leads to a phase factor
![]() $\exp [\text{i}\boldsymbol{x}_{0}\boldsymbol{\cdot }\boldsymbol{q}]$
multiplying the original Fourier coefficients
$\exp [\text{i}\boldsymbol{x}_{0}\boldsymbol{\cdot }\boldsymbol{q}]$
multiplying the original Fourier coefficients
![]() $\boldsymbol{V}(\boldsymbol{q},z,t)$
in (2.9). Consequently the amplitudes
$\boldsymbol{V}(\boldsymbol{q},z,t)$
in (2.9). Consequently the amplitudes
![]() $A_{0},B_{0}$
of the leading Fourier coefficients in (3.1) and in (3.2), (3.3) could be made real.
$A_{0},B_{0}$
of the leading Fourier coefficients in (3.1) and in (3.2), (3.3) could be made real.
Usually our simulations have started with general random initial conditions. To save computer time, in particular to construct standing waves, alternatively a kind of restricted initial conditions has been used. First they are based only on the Fourier coefficients with the wave vectors
![]() $\boldsymbol{q}_{1,2,3}$
which represent the functions
$\boldsymbol{q}_{1,2,3}$
which represent the functions
![]() $h(x,y)$
in appendix B. Furthermore the Fourier coefficients had to fulfil the phase restriction in (B 3) and (B 10d
–
f
). It was also helpful, for smaller changes of parameters to use already existing results.
$h(x,y)$
in appendix B. Furthermore the Fourier coefficients had to fulfil the phase restriction in (B 3) and (B 10d
–
f
). It was also helpful, for smaller changes of parameters to use already existing results.
Appendix B. Signature of subharmonic and oscillatory patterns in the DNS
A first impression of SH and OS patterns is simply obtained by looking at the corresponding DNS pictures and their time evolution, as done in §§ 3 and 4. In this section we discuss in more detail the SH and OS patterns in terms of the function
![]() $h(x,y;t)$
which derives from
$h(x,y;t)$
which derives from
![]() $\unicode[STIX]{x1D703}(x,y,z;t)$
at the midplane
$\unicode[STIX]{x1D703}(x,y,z;t)$
at the midplane
![]() $z=0$
, when keeping only the leading Fourier coefficients. These are directly provided by our pseudo-spectral code and their analysis gives an important clue to analysing SH and OS as discussed in the following subsections.
$z=0$
, when keeping only the leading Fourier coefficients. These are directly provided by our pseudo-spectral code and their analysis gives an important clue to analysing SH and OS as discussed in the following subsections.
B.1 The function
 $h(x,y,t)$
for SH patterns
$h(x,y,t)$
for SH patterns
The SH patterns are spanned by the dominant wave vectors
![]() $\boldsymbol{q}_{1}=(q_{c},0)$
and
$\boldsymbol{q}_{1}=(q_{c},0)$
and
![]() $\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y})$
. Thus
$\boldsymbol{q}_{2,3}=(q_{c}/2,\pm s_{y})$
. Thus
![]() $h(x,y)$
, the leading approximation of the midplane temperature
$h(x,y)$
, the leading approximation of the midplane temperature
![]() $\unicode[STIX]{x1D703}(x,y,z=0)$
introduced in § 3.1 is in general given as
$\unicode[STIX]{x1D703}(x,y,z=0)$
introduced in § 3.1 is in general given as
It turns out that
![]() $h(x,y)$
describes a perfect SH pattern when the phases of the Fourier coefficients allow the following representation:
$h(x,y)$
describes a perfect SH pattern when the phases of the Fourier coefficients allow the following representation:
with
![]() $\mathfrak{a}=\pm 1$
and the phase shift
$\mathfrak{a}=\pm 1$
and the phase shift
![]() $\unicode[STIX]{x1D713}$
. Obviously (B 3) is equivalent to
$\unicode[STIX]{x1D713}$
. Obviously (B 3) is equivalent to
The system is then only characterized by the moduli
![]() $A_{0},B_{0}$
of the Fourier coefficients as follows:
$A_{0},B_{0}$
of the Fourier coefficients as follows:
The phase shifts
![]() $\unicode[STIX]{x1D719}_{A}$
and
$\unicode[STIX]{x1D719}_{A}$
and
![]() $\unicode[STIX]{x1D713}$
can be put to zero by a shift of the origin of the
$\unicode[STIX]{x1D713}$
can be put to zero by a shift of the origin of the
![]() $x,y$
coordinate system and one arrives at the most simple representation of
$x,y$
coordinate system and one arrives at the most simple representation of
![]() $h(x,y)$
in (3.1).
$h(x,y)$
in (3.1).
We found that the procedure described above works also when a SH pattern appears only for finite time as in figure 14. One arrives then at time-dependent amplitudes
![]() $A_{0}(t),B_{0}(t)$
as shown in figure 15.
$A_{0}(t),B_{0}(t)$
as shown in figure 15.
B.2 The function
 $h(x,y,t)$
for OS patterns
$h(x,y,t)$
for OS patterns
The discussion of the OS patterns follows closely the one for SH patterns, though it is slightly more complicated since already the regular OS patterns oscillate in time. The OS patterns are spanned by the dominant wave vectors
![]() $\boldsymbol{q}_{1}=(q_{c},0)$
and
$\boldsymbol{q}_{1}=(q_{c},0)$
and
![]() $\boldsymbol{q}_{2,3}=(q_{c},\pm s_{y})$
. In addition it is useful to keep also the mode with wave vector
$\boldsymbol{q}_{2,3}=(q_{c},\pm s_{y})$
. In addition it is useful to keep also the mode with wave vector
![]() $\boldsymbol{q}_{4}=(0,s_{y})$
as a small correction.
$\boldsymbol{q}_{4}=(0,s_{y})$
as a small correction.
Thus in analogy to (B 1) we use the following ansatz for
![]() $h(x,y,t)$
:
$h(x,y,t)$
:
For travelling waves the phases of the Fourier coefficients have to fulfil the condition
with the frequency
![]() $\unicode[STIX]{x1D714}$
. In analogy to (B 4) we arrive at
$\unicode[STIX]{x1D714}$
. In analogy to (B 4) we arrive at
The system is then mainly characterized by the moduli
![]() $A_{0},B_{0}$
of the Fourier coefficients as before and in addition by the small correction
$A_{0},B_{0}$
of the Fourier coefficients as before and in addition by the small correction
![]() $D_{0}$
as
$D_{0}$
as
The amplitude
![]() $D_{0}$
vanishes at
$D_{0}$
vanishes at
![]() $\unicode[STIX]{x1D6FE}=0^{\circ }$
and increases then slowly with increasing
$\unicode[STIX]{x1D6FE}=0^{\circ }$
and increases then slowly with increasing
![]() $\unicode[STIX]{x1D6FE}$
. Again after a suitable shift of the origin of the coordinate system,
$\unicode[STIX]{x1D6FE}$
. Again after a suitable shift of the origin of the coordinate system,
![]() $\unicode[STIX]{x1D719}_{A}$
, and
$\unicode[STIX]{x1D719}_{A}$
, and
![]() $\unicode[STIX]{x1D713}$
can be put to zero and one arrives for
$\unicode[STIX]{x1D713}$
can be put to zero and one arrives for
![]() $h(x,y,t)$
in (3.2). The amplitudes
$h(x,y,t)$
in (3.2). The amplitudes
![]() $A_{0}$
,
$A_{0}$
,
![]() $B_{0}$
,
$B_{0}$
,
![]() $D_{0}$
are time independent for regular OS patterns as discussed in § 3.2. However, also intermediate travelling-wave patterns as in figure 18 are very well described by time dependent amplitudes
$D_{0}$
are time independent for regular OS patterns as discussed in § 3.2. However, also intermediate travelling-wave patterns as in figure 18 are very well described by time dependent amplitudes
![]() $A_{0}(t)$
and
$A_{0}(t)$
and
![]() $B_{0}(t)$
(see figure 19).
$B_{0}(t)$
(see figure 19).
Finally we come to the standing waves, which are represented as the travelling ones in (B 6) excepting some minor modifications in the complex amplitudes as follows: