Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-31T12:30:44.330Z Has data issue: false hasContentIssue false
  • English
  • Français

On the equatorial Ekman layer

Published online by Cambridge University Press:  30 August 2016

Florence Marcotte ,
Emmanuel Dormy  and
Andrew Soward
Florence Marcotte
Affiliation:
MAG (ENS/IPGP), LRA, Département de Physique, Ecole Normale Supérieure, 24, rue Lhomond, F-75231 Paris CEDEX 05, France
Emmanuel Dormy
Affiliation:
MAG (ENS/IPGP), LRA, Département de Physique, Ecole Normale Supérieure, 24, rue Lhomond, F-75231 Paris CEDEX 05, France
Andrew Soward*
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
*
†Email address for correspondence: andrew.soward@ncl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The steady incompressible viscous flow in the wide gap between spheres rotating rapidly about a common axis at slightly different rates (small Rossby number) has a long and celebrated history. The problem is relevant to the dynamics of geophysical and planetary core flows, for which, in the case of electrically conducting fluids, the possible operation of a dynamo is of considerable interest. A comprehensive asymptotic study, in the small Ekman number limit 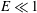$E\ll 1$ , was undertaken by Stewartson (J. Fluid Mech., vol. 26, 1966, pp. 131–144). The mainstream flow, exterior to the 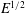$E^{1/2}$ Ekman layers on the inner/outer boundaries and the shear layer on the inner sphere tangent cylinder 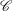$\mathscr{C}$ , is geostrophic. Stewartson identified a complicated nested layer structure on 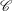$\mathscr{C}$ , which comprises relatively thick quasigeostrophic 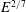$E^{2/7}$ - (inside 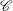$\mathscr{C}$ ) and 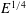$E^{1/4}$ - (outside 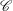$\mathscr{C}$ ) layers. They embed a thinner ageostrophic 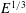$E^{1/3}$ shear layer (on 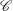$\mathscr{C}$ ), which merges with the inner sphere Ekman layer to form the 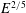$E^{2/5}$ -equatorial Ekman layer of axial length 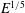$E^{1/5}$ . Under appropriate scaling, this 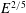$E^{2/5}$ -layer problem may be formulated, correct to leading order, independent of 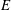$E$ . Then the Ekman boundary layer and ageostrophic shear layer become features of the far-field (as identified by the large value of the scaled axial coordinate $z$ ) solution. We present a numerical solution of the previously unsolved equatorial Ekman layer problem using a non-local integral boundary condition at finite $z$ to account for the far-field behaviour. Adopting 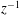$z^{-1}$ as a small parameter we extend Stewartson’s similarity solution for the ageostrophic shear layer to higher orders. This far-field solution agrees well with that obtained from our numerical model.

JFM classification

Boundary Layers: Boundary layer structure Boundary Layers: Free shear layers Geophysical and Geological Flows: Rotating flows

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 395 - 435
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

‡

Present address: Département de Mathématiques et Applications, CNRS UMR-8553, École Normale Supérieure, 45 rue d’Ulm, 75005 Paris, France

References

Abramowitz, M. & Stegun, I. A. 2010 NIST Handbook of Mathematical Functions (ed. Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W.), Cambridge University Press (available online http://dlmf.nist.gov/).Google Scholar
Aurnou, J., Andreadis, S., Zhu, L. & Olson, P. 2003 Experiments on convection in Earths core tangent cylinder. Earth Planet. Sci. Lett. 212, 119–134.CrossRefGoogle Scholar
Dormy, E. & Soward, A. M. 2007 Mathematical Aspects of Natural Dynamos (ed. Soward, A. M. & Ghil, M.), The Fluid Mechanics of Astrophysics and Geophysics, vol. 13, pp. 120–136. Chapman & Hall.CrossRefGoogle Scholar
Dormy, E., Cardin, P. & Jault, D. 1998 MHD flow in a slightly differentially rotating spherical shell, with conducting inner core, in a dipolar magnetic field. Earth Planet. Sci. Lett. 160, 15–39.Google Scholar
Dormy, E., Jaultc, D. & Soward, A. M. 2002 A super-rotating shear layer in magnetohydrodynamic spherical Couette flow. J. Fluid Mech. 452, 263–291.CrossRefGoogle Scholar
Dormy, E., Soward, A. M., Jones, C. A., Jault, D. & Cardin, P. 2004 The onset of thermal convection in rotating spherical shells. J. Fluid Mech. 501, 43–70.Google Scholar
Dowden, J. M. 1972 An equatorial boundary layer. J. Fluid Mech. 56, 193–200.Google Scholar
Gill, A. E. 1971 The equatorial current in a homogeneous ocean. Deep-Sea Res. 18, 421–431.Google Scholar
Glatzmaier, G. A. 2014 Introduction to Modeling Convection in Planets and Stars. Princeton University Press.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. Table of Integrals, Series, and Products (ed. Jeffrey, A. & Zwillinger, D.), Elsevier.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hide, R. & Titman, C. W. 1967 Detached shear layers in a rotating fluid. J. Fluid Mech. 29, 39–60.Google Scholar
Hollerbach, R. 2003 Instabilities of the Stewartson layer. Part 1. The dependence on the sign of Ro . J. Fluid Mech. 492, 289–302.Google Scholar
Hollerbach, R. & Proctor, M. R. E. 1993 Non-axisymmetric shear layers in a rotating spherical shell. In Solar and Planetary Dynamos (ed. Proctor, M. R. E. & Gilbert, A. D.), pp. 145–152. Cambridge University Press.Google Scholar
Hollerbach, R., Futterer, B., More, T. & Egbers, C. 2004 Instabilities of the Stewartson layer. Part 2: supercritical mode transitions. Theor. Comput. Fluid Dyn. 18, 197–204.Google Scholar
Kerswell, R. R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.CrossRefGoogle Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45, 035504.Google Scholar
Le Bars, M., Cébron, D. & Le Gal, P. 2015 Flows driven by libration, precession, and tides. Annu. Rev. Fluid Mech. 47, 163–193.CrossRefGoogle Scholar
Livermore, P. W. & Hollerbach, R. 2012 Successive elimination of shear layers by a hierarchy of constraints in inviscid spherical-shell flows. J. Math. Phys. 53, 073104.Google Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Phil. Trans. R. Soc. Lond. A 264 (1156), 597–634.Google Scholar
Pedlosky, J. 1979 Geophysical Fluid Dynamics. Springer.Google Scholar
Philander, S. G. H. 1971 On the flow properties of a fluid between concentric spheres form. J. Fluid Mech. 47, 799–809.CrossRefGoogle Scholar
Proudman, I. 1956 The almost-rigid rotation of viscous fluid between concentric spheres. J. Fluid Mech. 1, 505–516.Google Scholar
Roberts, P. H. 1967 Singularities of Hartmann layers. Proc. R. Soc. Lond. A 300, 94–107.Google Scholar
Roberts, P. H. 2003 Magnetohydrodynamics and the Earth’s Core: Selected works of Paul Roberts (ed. Soward, A. M. & Ghil, M.), The Fluid Mechanics of Astrophysics and Geophysics, vol. 10. Taylor & Francis.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76, 096801.CrossRefGoogle ScholarPubMed
Roberts, P. H. & Stewartson, K. 1963 On the stability of a Maclaurin spheroid with small viscocity. Astrophys. J. 137, 777–790.CrossRefGoogle Scholar
Rousset, R. 2007 Asymptotic behavior of geophysical fluids in highly rotating balls. Z. Angew. Math. Phys. 58, 53–67.CrossRefGoogle Scholar
Sakuraba, A. & Roberts, P. H. 2009 Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nature Geosci. 2, 802–805.CrossRefGoogle Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.CrossRefGoogle Scholar
Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26, 131–144.Google Scholar
Stewartson, K. & Rickard, J. R. A. 1970 Pathological oscillations of a rotating fluid. J. Fluid Mech. 35, 759–773.Google Scholar
Taylor, J. B. 1963 The magnetohydrodynamics of a rotating fluid and the Earth’s dynamo problem. Proc. R. Soc. Lond. A 274, 27–283.Google Scholar
van de Vooren, A. I. 1993 The connection between Ekman and Stewartson layers for a rotating disk. J. Engng Maths 27, 189–207.Google Scholar
Vo, T., Montabone, L., Read, P. L. & Sheard, G. J. 2015 Non-axisymmetric flows in a differential-disk rotating system. J. Fluid Mech. 775, 349–386.Google Scholar
Wei, X. & Hollerbach, R. 2008 Instabilities of Shercliffe and Stewartson layers in spherical Couette flow. Phy. Rev. E 78, 026309.Google Scholar