Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lee, Keunseob
Nishio, Yu
Izawa, Seiichiro
and
Fukunishi, Yu
2017.
Effects of location of excitation on the spiral vortices in the transitional region of a rotating-disk flow.
Physics of Fluids,
Vol. 29,
Issue. 8,
von Kurnatowski, Martin
Bortz, Michael
Klein, Peter
Kintzel, Birgit
and
Cremers, Carsten
2017.
Quantitative Kinetic Analysis of a PdAu3Alloy Catalyst for Oxygen Electro-Reduction.
Journal of The Electrochemical Society,
Vol. 164,
Issue. 14,
p.
H1072.
Thomas, Christian
and
Davies, Christopher
2018.
On the impulse response and global instability development of the infinite rotating-disc boundary layer.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
239.
Yim, Eunok
Chomaz, J.-M.
Martinand, D.
and
Serre, E.
2018.
Transition to turbulence in the rotating disk boundary layer of a rotor–stator cavity.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
631.
Keunseob, Lee
Yu, Nishio
Seiichiro, Izawa
and
Yu, Fukunishi
2018.
Growth of Spiral Vortices in a Globally Unstable Region on a Rotating Disk.
The Open Mechanical Engineering Journal,
Vol. 12,
Issue. 1,
p.
22.
Keunseob, Lee
Yu, Nishio
Seiichiro, Izawa
and
Yu, Fukunishi
2018.
Relation Between Convective Instability and Global Instability on a Rotating Disk.
The Open Mechanical Engineering Journal,
Vol. 12,
Issue. 1,
p.
37.
Arratia, Cristóbal
Mowlavi, Saviz
and
Gallaire, François
2018.
Absolute/convective secondary instabilities and the role of confinement in free shear layers.
Physical Review Fluids,
Vol. 3,
Issue. 5,
Appelquist, E.
Schlatter, P.
Alfredsson, P.H.
and
Lingwood, R.J.
2018.
Turbulence in the rotating-disk boundary layer investigated through direct numerical simulations.
European Journal of Mechanics - B/Fluids,
Vol. 70,
Issue. ,
p.
6.
Tilton, Nils
and
Martinand, Denis
2018.
Taylor–Couette–Poiseuille flow with a weakly permeable inner cylinder: absolute instabilities and selection of global modes.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
741.
Appelquist, E.
Schlatter, P.
Alfredsson, P. H.
and
Lingwood, R. J.
2018.
Transition to turbulence in the rotating-disk boundary-layer flow with stationary vortices.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
43.
Lee, K.
Nishio, Y.
Izawa, S.
and
Fukunishi, Y.
2018.
The effect of downstream turbulent region on the spiral vortex structures of a rotating-disk flow.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
274.
Thomas, Christian
and
Davies, Christopher
2019.
Global linear instability of rotating-cone boundary layers in a quiescent medium.
Physical Review Fluids,
Vol. 4,
Issue. 4,
Nevshupa, Roman
Castellote, Marta
Cornelio, Jesus Antonio Carlos
and
Toro, Alejandro
2020.
Triboemission of FINE and Ultrafine Aerosol Particles: A New Approach for Measurement and Accurate Quantification.
Lubricants,
Vol. 8,
Issue. 2,
p.
21.
Morgan, Scott
Davies, Christopher
and
Thomas, Christian
2021.
Control of stationary convective instabilities in the rotating disk boundary layer via time-periodic modulation.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Zhao, Zhizhou
Song, Wenwu
Jin, Yongxin
and
Lu, Jiaxing
2021.
Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity.
Applied Sciences,
Vol. 11,
Issue. 22,
p.
11000.
Thomas, Christian
and
Davies, Christopher
2021.
An adjoint approach for computing the receptivity of the rotating disc boundary layer to surface roughness.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Morgan, Scott
Davies, Christopher
and
Thomas, Christian
2022.
Linear impulse response in three-dimensional oscillatory boundary layers formed by periodic modulation of a rotating disk.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
KATO, Kentaro
LINGWOOD, Rebecca J.
and
ALFREDSSON, P. Henrik
2023.
Rotating disks and cones a centennial of von Kármán’s 1921 paper.
Journal of Fluid Science and Technology,
Vol. 18,
Issue. 1,
p.
JFST0003.
Thomas, Christian
Alveroğlu, Burhan
Stephen, Sharon O.
Al-Malki, Mushrifah A. S.
and
Hussain, Zahir
2023.
Effect of slip on the linear stability of the rotating disk boundary layer.
Physics of Fluids,
Vol. 35,
Issue. 8,
Martinand, D.
Serre, E.
and
Viaud, B.
2023.
Instabilities and routes to turbulence in rotating disc boundary layers and cavities.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2243,
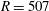 $R=507$ . Instead, the front approaches
$R=507$ . Instead, the front approaches 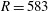 $R=583$ and both the temporal frequency and spatial growth rate correspond to a global mode originating at this position.
$R=583$ and both the temporal frequency and spatial growth rate correspond to a global mode originating at this position.

