Article contents
On the identification of well-behaved turbulent boundary layers
Published online by Cambridge University Press: 31 May 2017
Abstract
This paper introduces a new method based on the diagnostic plot (Alfredsson et al., Phys. Fluids, vol. 23, 2011, 041702) to assess the convergence towards a well-behaved zero-pressure-gradient (ZPG) turbulent boundary layer (TBL). The most popular and well-understood methods to assess the convergence towards a well-behaved state rely on empirical skin-friction curves (requiring accurate skin-friction measurements), shape-factor curves (requiring full velocity profile measurements with an accurate wall position determination) or wake-parameter curves (requiring both of the previous quantities). On the other hand, the proposed diagnostic-plot method only needs measurements of mean and fluctuating velocities in the outer region of the boundary layer at arbitrary wall-normal positions. To test the method, six tripping configurations, including optimal set-ups as well as both under- and overtripped cases, are used to quantify the convergence of ZPG TBLs towards well-behaved conditions in the Reynolds-number range covered by recent high-fidelity direct numerical simulation data up to a Reynolds number based on the momentum thickness and free-stream velocity 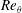 $Re_{\unicode[STIX]{x1D703}}$ of approximately 4000 (corresponding to 2.5 m from the leading edge) in a wind-tunnel experiment. Additionally, recent high-Reynolds-number data sets have been employed to validate the method. The results show that weak tripping configurations lead to deviations in the mean flow and the velocity fluctuations within the logarithmic region with respect to optimally tripped boundary layers. On the other hand, a strong trip leads to a more energized outer region, manifested in the emergence of an outer peak in the velocity-fluctuation profile and in a more prominent wake region. While established criteria based on skin-friction and shape-factor correlations yield generally equivalent results with the diagnostic-plot method in terms of convergence towards a well-behaved state, the proposed method has the advantage of being a practical surrogate that is a more efficient tool when designing the set-up for TBL experiments, since it diagnoses the state of the boundary layer without the need to perform extensive velocity profile measurements.
$Re_{\unicode[STIX]{x1D703}}$ of approximately 4000 (corresponding to 2.5 m from the leading edge) in a wind-tunnel experiment. Additionally, recent high-Reynolds-number data sets have been employed to validate the method. The results show that weak tripping configurations lead to deviations in the mean flow and the velocity fluctuations within the logarithmic region with respect to optimally tripped boundary layers. On the other hand, a strong trip leads to a more energized outer region, manifested in the emergence of an outer peak in the velocity-fluctuation profile and in a more prominent wake region. While established criteria based on skin-friction and shape-factor correlations yield generally equivalent results with the diagnostic-plot method in terms of convergence towards a well-behaved state, the proposed method has the advantage of being a practical surrogate that is a more efficient tool when designing the set-up for TBL experiments, since it diagnoses the state of the boundary layer without the need to perform extensive velocity profile measurements.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 47
- Cited by


