We study the longitudinal linear optimal perturbations (which maximize the energy gain up to a prescribed time 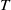$T$) to inviscid parallel shear flow, which present unbounded energy growth due to the lift-up mechanism. Using the phase invariance with respect to time, we show that for an arbitrary base flow profile and optimization time, the computation of the optimal longitudinal perturbation reduces to the resolution of a single one-dimensional eigenvalue problem valid for all times. The optimal perturbation and its amplification are then derived from the lowest eigenvalue and its associated eigenfunction, while the remainder of the infinite set of eigenfunctions provides an orthogonal base for decomposing the evolution of arbitrary perturbations. With this new formulation we obtain, asymptotically for large spanwise wavenumber 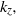${k}_{z} , $ a prediction of the optimal gain and the localization of inviscid optimal perturbations for the two main classes of parallel flows: free shear flow with an inflectional velocity profile, and wall-bounded flow with maximum shear at the wall. We show that the inviscid optimal perturbations are localized around the point of maximum shear in a region with a width scaling like 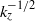${ k}_{z}^{- 1/ 2} $ for free shear flow, and like 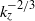${ k}_{z}^{- 2/ 3} $ for wall-bounded shear flows. This new derivation uses the stationarity of the base flow to transform the optimization of initial conditions in phase space into the optimization of a temporal phase along each trajectory, and an optimization among all trajectories labelled by their intersection with a codimension-1 subspace. The optimization of the time phase directly imposes that the initial and final energy growth rates of the optimal perturbation should be equal. This result requires only time invariance of the base flow, and is therefore valid for any linear optimal perturbation problem with stationary base flow.