Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
He, Long
and
Tafti, Danesh
2018.
Variation of drag, lift and torque in a suspension of ellipsoidal particles.
Powder Technology,
Vol. 335,
Issue. ,
p.
409.
Zarghami, Ahad
and
Padding, Johan T.
2018.
Drag, lift and torque acting on a two-dimensional non-spherical particle near a wall.
Advanced Powder Technology,
Vol. 29,
Issue. 6,
p.
1507.
Sanjeevi, Sathish K. P.
Zarghami, Ahad
and
Padding, Johan T.
2018.
Choice of no-slip curved boundary condition for lattice Boltzmann simulations of high-Reynolds-number flows.
Physical Review E,
Vol. 97,
Issue. 4,
Chen, Y.
and
Müller, C.R.
2018.
Development of a drag force correlation for assemblies of cubic particles: The effect of solid volume fraction and Reynolds number.
Chemical Engineering Science,
Vol. 192,
Issue. ,
p.
1157.
Mahajan, Vinay V.
Padding, Johan T.
Nijssen, Tim M. J.
Buist, Kay A.
and
Kuipers, J. A. M.
2018.
Nonspherical particles in a pseudo‐2D fluidized bed: Experimental study.
AIChE Journal,
Vol. 64,
Issue. 5,
p.
1573.
Cao, Ze
and
Tafti, Danesh K.
2018.
Investigation of drag, lift and torque for fluid flow past a low aspect ratio (1:4) cylinder.
Computers & Fluids,
Vol. 177,
Issue. ,
p.
123.
Sanjeevi, Sathish K.P.
Kuipers, J.A.M.
and
Padding, Johan T.
2018.
Drag, lift and torque correlations for non-spherical particles from Stokes limit to high Reynolds numbers.
International Journal of Multiphase Flow,
Vol. 106,
Issue. ,
p.
325.
Chinnappan, Arun K.
Kumar, Rakesh
Arghode, Vaibhav K.
and
Myong, Rho Shin
2019.
Transport dynamics of an ellipsoidal particle in free molecular gas flow regime.
Physics of Fluids,
Vol. 31,
Issue. 3,
Pierson, Jean-Lou
Auguste, Franck
Hammouti, Abdelkader
and
Wachs, Anthony
2019.
Inertial flow past a finite-length axisymmetric cylinder of aspect ratio 3: Effect of the yaw angle.
Physical Review Fluids,
Vol. 4,
Issue. 4,
El Hasadi, Yousef M. F.
and
Padding, Johan T.
2019.
Solving fluid flow problems using semi-supervised symbolic regression on sparse data.
AIP Advances,
Vol. 9,
Issue. 11,
Mema, Ivan
Mahajan, Vinay V.
Fitzgerald, Barry W.
and
Padding, Johan T.
2019.
Effect of lift force and hydrodynamic torque on fluidisation of non-spherical particles.
Chemical Engineering Science,
Vol. 195,
Issue. ,
p.
642.
Andersson, Helge I.
and
Jiang, Fengjian
2019.
Forces and torques on a prolate spheroid: low-Reynolds-number and attack angle effects.
Acta Mechanica,
Vol. 230,
Issue. 2,
p.
431.
Zarghami, Ahad
Ashorynejad, Hamid Reza
and
Padding, Johan T.
2019.
Hydrodynamics forces on a circular particle near a sinusoidal corrugated wall.
Powder Technology,
Vol. 342,
Issue. ,
p.
789.
Andersson, Helge I.
Jiang, Fengjian
and
Okulov, Valery L.
2019.
Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics.
Vol. 50,
Issue. ,
p.
311.
Fitzgerald, Barry W.
Zarghami, Ahad
Mahajan, Vinay V.
Sanjeevi, Sathish K.P.
Mema, Ivan
Verma, Vikrant
El Hasadi, Yousef M.F.
and
Padding, Johan T.
2019.
Multiscale simulation of elongated particles in fluidised beds.
Chemical Engineering Science: X,
Vol. 2,
Issue. ,
p.
100019.
Cai, Shiying
Cai, Chunpei
and
Li, Jun
2020.
Highly dilute gas flows over an ellipse.
Physics of Fluids,
Vol. 32,
Issue. 9,
Ouchene, R.
2020.
Numerical simulation and modeling of the hydrodynamic forces and torque acting on individual oblate spheroids.
Physics of Fluids,
Vol. 32,
Issue. 7,
Mema, Ivan
Wagner, Evert C.
van Ommen, J. Ruud
and
Padding, Johan T.
2020.
Fluidization of spherical versus elongated particles - experimental investigation using X-ray tomography.
Chemical Engineering Journal,
Vol. 397,
Issue. ,
p.
125203.
He, Shengrong
Li, Yanfeng
Liu, Taishan
Chen, Peng
Zhao, Yanfeng
and
Yin, Mao
2020.
A novel model for critical motion of particles in inclined channels of liquid-solid separation fluidized bed.
Powder Technology,
Vol. 369,
Issue. ,
p.
289.
Wu, Mingqiu
Peters, Bernhard
Rosemann, Tony
and
Kruggel-Emden, Harald
2020.
A forcing fictitious domain method to simulate fluid-particle interaction of particles with super-quadric shape.
Powder Technology,
Vol. 360,
Issue. ,
p.
264.
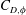 $C_{D,\unicode[STIX]{x1D719}}$ at different incident angles
$C_{D,\unicode[STIX]{x1D719}}$ at different incident angles 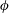 $\unicode[STIX]{x1D719}$ for a wide range of Reynolds numbers (
$\unicode[STIX]{x1D719}$ for a wide range of Reynolds numbers ( 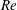 $\mathit{Re}$ ). We show that the sine-squared drag law
$\mathit{Re}$ ). We show that the sine-squared drag law  $C_{D,\unicode[STIX]{x1D719}}=C_{D,\unicode[STIX]{x1D719}=0^{\circ }}+(C_{D,\unicode[STIX]{x1D719}=90^{\circ }}-C_{D,\unicode[STIX]{x1D719}=0^{\circ }})\sin ^{2}\unicode[STIX]{x1D719}$ holds up to large Reynolds numbers,
$C_{D,\unicode[STIX]{x1D719}}=C_{D,\unicode[STIX]{x1D719}=0^{\circ }}+(C_{D,\unicode[STIX]{x1D719}=90^{\circ }}-C_{D,\unicode[STIX]{x1D719}=0^{\circ }})\sin ^{2}\unicode[STIX]{x1D719}$ holds up to large Reynolds numbers, 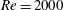 $\mathit{Re}=2000$ . Further, we explore the physical origin behind the sine-squared law, and reveal that, surprisingly, this does not occur due to linearity of flow fields. Instead, it occurs due to an interesting pattern of pressure distribution contributing to the drag at higher
$\mathit{Re}=2000$ . Further, we explore the physical origin behind the sine-squared law, and reveal that, surprisingly, this does not occur due to linearity of flow fields. Instead, it occurs due to an interesting pattern of pressure distribution contributing to the drag at higher 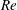 $\mathit{Re}$ for different incident angles. The present results demonstrate that it is possible to perform just two simulations at
$\mathit{Re}$ for different incident angles. The present results demonstrate that it is possible to perform just two simulations at  $\unicode[STIX]{x1D719}=0^{\circ }$ and
$\unicode[STIX]{x1D719}=0^{\circ }$ and 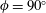 $\unicode[STIX]{x1D719}=90^{\circ }$ for a given
$\unicode[STIX]{x1D719}=90^{\circ }$ for a given 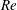 $\mathit{Re}$ and obtain particle-shape-specific
$\mathit{Re}$ and obtain particle-shape-specific 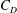 $C_{D}$ at arbitrary incident angles. However, the model has limited applicability to flatter oblate spheroids, which do not exhibit the sine-squared interpolation, even for
$C_{D}$ at arbitrary incident angles. However, the model has limited applicability to flatter oblate spheroids, which do not exhibit the sine-squared interpolation, even for 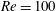 $\mathit{Re}=100$ , due to stronger wake-induced drag. Regarding lift coefficients, we find that the equivalent theoretical equation can provide a reasonable approximation, even at high
$\mathit{Re}=100$ , due to stronger wake-induced drag. Regarding lift coefficients, we find that the equivalent theoretical equation can provide a reasonable approximation, even at high 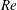 $\mathit{Re}$ , for prolate spheroids.
$\mathit{Re}$ , for prolate spheroids.

