Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Carini, M.
Giannetti, F.
and
Auteri, F.
2014.
First instability and structural sensitivity of the flow past two side-by-side cylinders.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
627.
Luchini, Paolo
and
Bottaro, Alessandro
2014.
Adjoint Equations in Stability Analysis.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
493.
Chen, Weilin
Ji, Chunning
Xu, Wanhai
Liu, Shuang
and
Campbell, Jordan
2015.
Response and wake patterns of two side-by-side elastically supported circular cylinders in uniform laminar cross-flow.
Journal of Fluids and Structures,
Vol. 55,
Issue. ,
p.
218.
Camarri, Simone
2015.
Flow control design inspired by linear stability analysis.
Acta Mechanica,
Vol. 226,
Issue. 4,
p.
979.
Citro, V.
Giannetti, F.
Luchini, P.
and
Auteri, F.
2015.
Global stability and sensitivity analysis of boundary-layer flows past a hemispherical roughness element.
Physics of Fluids,
Vol. 27,
Issue. 8,
Chen, Weilin
Ji, Chunning
Wang, Rui
Xu, Dong
and
Campbell, Jordan
2015.
Flow-induced vibrations of two side-by-side circular cylinders: Asymmetric vibration, symmetry hysteresis and near-wake patterns.
Ocean Engineering,
Vol. 110,
Issue. ,
p.
244.
Peng, Yih Ferng
and
Sau, Amalendu
2015.
Transitional hysteresis loop and coexistence of synchronized shedding in coupled wakes.
Physics of Fluids,
Vol. 27,
Issue. 7,
Carini, M.
Auteri, F.
and
Giannetti, F.
2015.
Centre-manifold reduction of bifurcating flows.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
109.
Citro, V.
Luchini, P.
Giannetti, F.
and
Auteri, F.
2015.
Boundary-layer Flows Past an Hemispherical Roughness Element: DNS, Global Stability and Sensitivity Analysis.
Procedia IUTAM,
Vol. 14,
Issue. ,
p.
173.
Bai, Xiao-Dong
Zhang, Wei
Guo, An-Xin
and
Wang, Yong
2016.
The flip-flopping wake pattern behind two side-by-side circular cylinders: A global stability analysis.
Physics of Fluids,
Vol. 28,
Issue. 4,
Singha, Sintu
Nagarajan, Kaushik Kumar
and
Sinhamahapatra, K. P.
2016.
Numerical study of two-dimensional flow around two side-by-side circular cylinders at low Reynolds numbers.
Physics of Fluids,
Vol. 28,
Issue. 5,
Liu, Bin
and
Jaiman, Rajeev K.
2016.
Interaction dynamics of gap flow with vortex-induced vibration in side-by-side cylinder arrangement.
Physics of Fluids,
Vol. 28,
Issue. 12,
Ma, Shengwei
Kang, Chang-Wei
Lim, Teck-Bin Arthur
Wu, Chih-Hua
and
Tutty, Owen
2017.
Wake of two side-by-side square cylinders at low Reynolds numbers.
Physics of Fluids,
Vol. 29,
Issue. 3,
Alam, Md. Mahbub
Zheng, Qinmin
and
Hourigan, Kerry
2017.
The wake and thrust by four side-by-side cylinders at a low Re.
Journal of Fluids and Structures,
Vol. 70,
Issue. ,
p.
131.
Citro, V.
Luchini, P.
Giannetti, F.
and
Auteri, F.
2017.
Efficient stabilization and acceleration of numerical simulation of fluid flows by residual recombination.
Journal of Computational Physics,
Vol. 344,
Issue. ,
p.
234.
Canton, J.
Auteri, F.
and
Carini, M.
2017.
Linear global stability of two incompressible coaxial jets.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
886.
Bao, Y.
Zhou, D.
Tao, J. J.
Peng, Z.
Zhu, H. B.
Sun, Z. L.
and
Tong, H. L.
2017.
Dynamic interference of two anti-phase flapping foils in side-by-side arrangement in an incompressible flow.
Physics of Fluids,
Vol. 29,
Issue. 3,
Carini, M.
Airiau, C.
Debien, A.
Léon, O.
and
Pralits, J. O.
2017.
Global stability and control of the confined turbulent flow past a thick flat plate.
Physics of Fluids,
Vol. 29,
Issue. 2,
de Paula, Alexandre Vagtinski
and
Möller, Sergio Viçosa
2018.
On the chaotic nature of bistable flows.
Experimental Thermal and Fluid Science,
Vol. 94,
Issue. ,
p.
172.
Shi, Liuliu
Yang, Geer
and
Yao, Shichuan
2018.
Large eddy simulation of flow past a square cylinder with rounded leading corners: A comparison of 2D and 3D approaches.
Journal of Mechanical Science and Technology,
Vol. 32,
Issue. 6,
p.
2671.
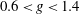 $0.6<g<1.4$ and Reynolds number
$0.6<g<1.4$ and Reynolds number 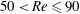 $50<Re\leq 90$ . The inherent two-dimensional flow pattern is characterized by an asymmetric unsteady wake (with respect to the horizontal axis of symmetry) with the gap flow being deflected alternatively toward one of the cylinders. Such behaviour has been ascribed by other authors to a bistability of the flow, and therefore termed flip–flop. In contrast, the simulations performed herein provide new evidence that at low Reynolds numbers the flip–flopping state develops through an instability of the in-phase synchronized vortex shedding between the two cylinder wakes. This new scenario is confirmed and explained by means of a linear global stability investigation of the in-phase periodic base flow. The Floquet analysis reveals indeed that a pair of complex-conjugate multipliers becomes unstable having the same low frequency as the gap flow flip-over. The neutral curve of this secondary instability is tracked within the above range of gap spacing. The spatiotemporal shape of the unstable Floquet mode is then analysed and its structural sensitivity is considered in order to identify the ‘core’ region of the flip–flop instability mechanism.
$50<Re\leq 90$ . The inherent two-dimensional flow pattern is characterized by an asymmetric unsteady wake (with respect to the horizontal axis of symmetry) with the gap flow being deflected alternatively toward one of the cylinders. Such behaviour has been ascribed by other authors to a bistability of the flow, and therefore termed flip–flop. In contrast, the simulations performed herein provide new evidence that at low Reynolds numbers the flip–flopping state develops through an instability of the in-phase synchronized vortex shedding between the two cylinder wakes. This new scenario is confirmed and explained by means of a linear global stability investigation of the in-phase periodic base flow. The Floquet analysis reveals indeed that a pair of complex-conjugate multipliers becomes unstable having the same low frequency as the gap flow flip-over. The neutral curve of this secondary instability is tracked within the above range of gap spacing. The spatiotemporal shape of the unstable Floquet mode is then analysed and its structural sensitivity is considered in order to identify the ‘core’ region of the flip–flop instability mechanism.
