Article contents
On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface
Published online by Cambridge University Press: 19 August 2014
Abstract
We investigate the shock-induced turbulent mixing between a light and a heavy gas, where a Richtmyer–Meshkov instability (RMI) is initiated by a shock wave with Mach number 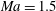 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ma}= 1.5$ . The prescribed initial conditions define a deterministic multimode interface perturbation between the gases, which can be imposed exactly for different simulation codes and resolutions to allow for quantitative comparison. Well-resolved large-eddy simulations are performed using two different and independently developed numerical methods with the objective of assessing turbulence structures, prediction uncertainties and convergence behaviour. The two numerical methods differ fundamentally with respect to the employed subgrid-scale regularisation, each representing state-of-the-art approaches to RMI. Unlike previous studies, the focus of the present investigation is to quantify the uncertainties introduced by the numerical method, as there is strong evidence that subgrid-scale regularisation and truncation errors may have a significant effect on the linear and nonlinear stages of the RMI evolution. Fourier diagnostics reveal that the larger energy-containing scales converge rapidly with increasing mesh resolution and thus are in excellent agreement for the two numerical methods. Spectra of gradient-dependent quantities, such as enstrophy and scalar dissipation rate, show stronger dependences on the small-scale flow field structures as a consequence of truncation error effects, which for one numerical method are dominantly dissipative and for the other dominantly dispersive. Additionally, the study reveals details of various stages of RMI, as the flow transitions from large-scale nonlinear entrainment to fully developed turbulent mixing. The growth rates of the mixing zone widths as obtained by the two numerical methods are
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ma}= 1.5$ . The prescribed initial conditions define a deterministic multimode interface perturbation between the gases, which can be imposed exactly for different simulation codes and resolutions to allow for quantitative comparison. Well-resolved large-eddy simulations are performed using two different and independently developed numerical methods with the objective of assessing turbulence structures, prediction uncertainties and convergence behaviour. The two numerical methods differ fundamentally with respect to the employed subgrid-scale regularisation, each representing state-of-the-art approaches to RMI. Unlike previous studies, the focus of the present investigation is to quantify the uncertainties introduced by the numerical method, as there is strong evidence that subgrid-scale regularisation and truncation errors may have a significant effect on the linear and nonlinear stages of the RMI evolution. Fourier diagnostics reveal that the larger energy-containing scales converge rapidly with increasing mesh resolution and thus are in excellent agreement for the two numerical methods. Spectra of gradient-dependent quantities, such as enstrophy and scalar dissipation rate, show stronger dependences on the small-scale flow field structures as a consequence of truncation error effects, which for one numerical method are dominantly dissipative and for the other dominantly dispersive. Additionally, the study reveals details of various stages of RMI, as the flow transitions from large-scale nonlinear entrainment to fully developed turbulent mixing. The growth rates of the mixing zone widths as obtained by the two numerical methods are 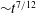 ${\sim } t^{7/12}$ before re-shock and
${\sim } t^{7/12}$ before re-shock and 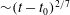 ${\sim } (t-t_0)^{2/7}$ long after re-shock. The decay rate of turbulence kinetic energy is consistently
${\sim } (t-t_0)^{2/7}$ long after re-shock. The decay rate of turbulence kinetic energy is consistently 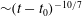 ${\sim } (t-t_0)^{-10/7}$ at late times, where the molecular mixing fraction approaches an asymptotic limit
${\sim } (t-t_0)^{-10/7}$ at late times, where the molecular mixing fraction approaches an asymptotic limit  $\varTheta \approx 0.85$ . The anisotropy measure
$\varTheta \approx 0.85$ . The anisotropy measure 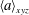 $\langle a \rangle _{xyz}$ approaches an asymptotic limit of
$\langle a \rangle _{xyz}$ approaches an asymptotic limit of 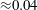 ${\approx }0.04$ , implying that no full recovery of isotropy within the mixing zone is obtained, even after re-shock. Spectra of density, turbulence kinetic energy, scalar dissipation rate and enstrophy are presented and show excellent agreement for the resolved scales. The probability density function of the heavy-gas mass fraction and vorticity reveal that the light–heavy gas composition within the mixing zone is accurately predicted, whereas it is more difficult to capture the long-term behaviour of the vorticity.
${\approx }0.04$ , implying that no full recovery of isotropy within the mixing zone is obtained, even after re-shock. Spectra of density, turbulence kinetic energy, scalar dissipation rate and enstrophy are presented and show excellent agreement for the resolved scales. The probability density function of the heavy-gas mass fraction and vorticity reveal that the light–heavy gas composition within the mixing zone is accurately predicted, whereas it is more difficult to capture the long-term behaviour of the vorticity.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 112
- Cited by

