Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T19:21:08.225Z Has data issue: false hasContentIssue false
  • English
  • Français

On the stability of the μ(I) rheology for granular flow

Published online by Cambridge University Press:  03 November 2017

J. D. Goddard Open the ORCID record for J. D. Goddard [Opens in a new window]  and
Jaesung Lee
J. D. Goddard
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0411, USA
Jaesung Lee
Affiliation:
Department of Chemical and Environmental Technology, Inha Technical College, 100 Inha-ro, Nam-gu, Incheon, 22212, Republic of Korea
Get access Rights & Permissions [Opens in a new window]

Abstract

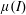This article deals with the Hadamard instability of the so-called $\unicode[STIX]{x1D707}(I)$ model of dense rapidly sheared granular flow, as reported recently by Barker et al. (J. Fluid Mech., vol. 779, 2015, pp. 794–818). The present paper presents a more comprehensive study of the linear stability of planar simple shearing and pure shearing flows, with account taken of convective Kelvin wavevector stretching by the base flow. We provide a closed-form solution for the linear-stability problem and show that wavevector stretching leads to asymptotic stabilization of the non-convective instability found by Barker et al. (J. Fluid Mech., vol. 779, 2015, pp. 794–818). We also explore the stabilizing effects of higher velocity gradients achieved by an enhanced-continuum model based on a dissipative analogue of the van der Waals–Cahn–Hilliard equation of equilibrium thermodynamics. This model involves a dissipative hyperstress, as the analogue of a special Korteweg stress, with surface viscosity representing the counterpart of elastic surface tension. Based on the enhanced-continuum model, we also present a model of steady shear bands and their nonlinear stability against parallel shearing. Finally, we propose a theoretical connection between the non-convective instability of Barker et al. (J. Fluid Mech., vol. 779, 2015, pp. 794–818) and the loss of generalized ellipticity in the quasi-static field equations. Apart from the theoretical interest, the present work may suggest stratagems for the numerical simulation of continuum field equations involving the 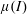$\unicode[STIX]{x1D707}(I)$ rheology and variants thereof.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 302 - 331
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Nott, P. 1997 The influence of friction on the stability of unbounded granular shear flow. J. Fluid Mech. 343, 267–301.CrossRefGoogle Scholar
Anderson, D. M., McFadden, G. B. & Wheeler, A. A. 1998 Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30 (1), 139–165.CrossRefGoogle Scholar
Barker, T. & Gray, N. 2017 Partial regularisation of the incompressible 𝜇(I)-rheology for granular flow. J. Fluid Mech. 828, 5–32.CrossRefGoogle Scholar
Barker, T., Schaeffer, D., Shearer, M. & Gray, N. 2017 Well-posed continuum equations for granular flow with compressibility and 𝜇(I)-rheology. Proc. R. Soc. Lond. A 473 (2201), 20160846.Google ScholarPubMed
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T. 2015 Well-posed and ill-posed behaviour of the 𝜇(I)-rheology for granular flow. J. Fluid Mech. 779, 794–818.CrossRefGoogle Scholar
Belytschko, T., Chiang, H.-Y. & Plaskacz, E. 1994 High resolution two-dimensional shear band computations: imperfections and mesh dependence. Comput. Meth. Appl. Mech. Engng 119 (1–2), 1–15.CrossRefGoogle Scholar
Bigoni, D. 1995 On flutter instability in elastoplastic constitutive models. Intl J. Solids Struct. 32 (21), 3167–3189.CrossRefGoogle Scholar
Brezis, H. & Browder, F. 1998 Partial differential equations in the 20th century. Adv. Maths 135 (1), 76–144.CrossRefGoogle Scholar
Browder, F. 1961 On the spectral theory of elliptic differential operators. I. Math. Ann. 142 (1), 22–130.CrossRefGoogle Scholar
Cahn, J. W. & Hilliard, J. E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.CrossRefGoogle Scholar
Didwania, A. K. & Goddard, J. D. 1993 A note on the generalized Rayleigh quotient for non-self-adjoint linear stability operators. Phys. Fluids A 5 (5), 1269–1271.CrossRefGoogle Scholar
Edelen, D. G. B. 1972 A nonlinear Onsager theory of irreversibility. Intl J. Engng Sci. 10 (6), 481–490.CrossRefGoogle Scholar
Edelen, D. G. B. 2005 Applied Exterior Calculus. Dover.Google Scholar
Forest, S. & Aifantis, E. 2010 Some links between recent gradient thermo-elasto-plasticity theories and the thermomechanics of generalized continua. Intl J. Solids Struct. 47 (25), 3367–3376.CrossRefGoogle Scholar
Fornberg, B. 1988 Generation of finite difference formulas on arbitrarily spaced grids. Maths Comput. 51 (184), 699–706.CrossRefGoogle Scholar
Goddard, J. D. 2003 Material instability in complex fluids. Annu. Rev. Fluid Mech. 35 (1), 113–133.CrossRefGoogle Scholar
Goddard, J. D. 2014 Edelen’s dissipation potentials and the visco-plasticity of particulate media. Acta Mechanica 225 (8), 2239–2259.CrossRefGoogle Scholar
Gurtin, M. E. 1996 Generalized Ginzburg–Landau and Cahn–Hilliard equations based on a microforce balance. Physica D 92 (3), 178–192.Google Scholar
Henann, D. L. & Kamrin, K. 2014 Continuum thermomechanics of the nonlocal granular rheology. Intl J. Plasticity 60, 145–162.CrossRefGoogle Scholar
Heyman, J., Delannay, R., Tabuteau, H. & Valance, A. 2016 Compressibility regularizes the 𝜇(I)-rheology for granular flows. J. Fluid Mech. 830, 553–568.CrossRefGoogle Scholar
Hill, R. 1956 New horizons in the mechanics of solids. J. Mech. Phys. Solids 5 (1), 66–74.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.CrossRefGoogle Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.CrossRefGoogle ScholarPubMed
Leonov, A. I. 1988 Extremum principles and exact two-side bounds of potential: functional and dissipation for slow motions of nonlinear viscoplastic media. J. Non-Newtonian Fluid Mech. 28 (1), 1–28.CrossRefGoogle Scholar
MiDi, GDR 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Mindlin, R. D. 1964 Micro-structure in linear elasticity. Arch. Rat. Mech. Anal. 16 (1), 51–78.CrossRefGoogle Scholar
Pouliquen, O. & Forterre, Y. 2009 A non-local rheology for dense granular flows. Phil. Trans. R. Soc. Lond. A 367 (1909), 5091–5107.Google ScholarPubMed
Renardy, M. & Rogers, R. 2006 An Introduction to Partial Differential Equations. Springer.Google Scholar
Rowlinson, J. S. 1979 Translation of J. D. van der Waals’ ‘The thermodynamik theory of capillarity under the hypothesis of a continuous variation of density’. J. Stat. Phys. 20 (2), 197–200.CrossRefGoogle Scholar
Saramito, P. 2016 Complex Fluids – Modeling and Algorithms. SMAI/Springer Int. Publishing.CrossRefGoogle Scholar
Schiesser, W. E. 2012 The Numerical Method of Lines: Integration of Partial Differential Equations. Elsevier.Google Scholar
Thomson, W. 1887 XXI. Stability of fluid motions (continued from the May and June numbers) – rectilineal motion of viscous fluid between two parallel planes. Phil. Mag. 24 (147), 188–196.CrossRefGoogle Scholar
Trefethen, L. & Embree, M. 2005 Spectra and Pseudospectra: the Behavior of Nonnormal Matrices and Operators. Princeton University Press.CrossRefGoogle Scholar