Article contents
On the structure and origin of pressure fluctuations in wall turbulence: predictions based on the resolvent analysis
Published online by Cambridge University Press: 16 June 2014
Abstract
We generate predictions for the fluctuating pressure field in turbulent pipe flow by reformulating the resolvent analysis of McKeon and Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382) in terms of the so-called primitive variables. Under this analysis, the nonlinear convective terms in the Fourier-transformed Navier–Stokes equations (NSE) are treated as a forcing that is mapped to a velocity and pressure response by the resolvent of the linearized Navier–Stokes operator. At each wavenumber–frequency combination, the turbulent velocity and pressure field are represented by the most-amplified (rank-1) response modes, identified via a singular value decomposition of the resolvent. We show that these rank-1 response modes reconcile many of the key relationships among the velocity field, coherent structure (i.e. hairpin vortices), and the high-amplitude wall-pressure events observed in previous experiments and direct numerical simulations (DNS). A Green’s function representation shows that the pressure fields obtained under this analysis correspond primarily to the fast pressure contribution arising from the linear interaction between the mean shear and the turbulent wall-normal velocity. Recovering the slow pressure requires an explicit treatment of the nonlinear interactions between the Fourier response modes. By considering the velocity and pressure fields associated with the triadically consistent mode combination studied by Sharma and McKeon (J. Fluid Mech., vol. 728, 2013, pp. 196–238), we identify the possibility of an apparent amplitude modulation effect in the pressure field, similar to that observed for the streamwise velocity field. However, unlike the streamwise velocity, for which the large scales of the flow are in phase with the envelope of the small-scale activity close to the wall, we expect there to be a 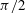 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\pi /2$ phase difference between the large-scale wall-pressure and the envelope of the small-scale activity. Finally, we generate spectral predictions based on a rank-1 model assuming broadband forcing across all wavenumber–frequency combinations. Despite the significant simplifying assumptions, this approach reproduces trends observed in previous DNS for the wavenumber spectra of velocity and pressure, and for the scale-dependence of wall-pressure propagation speed.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\pi /2$ phase difference between the large-scale wall-pressure and the envelope of the small-scale activity. Finally, we generate spectral predictions based on a rank-1 model assuming broadband forcing across all wavenumber–frequency combinations. Despite the significant simplifying assumptions, this approach reproduces trends observed in previous DNS for the wavenumber spectra of velocity and pressure, and for the scale-dependence of wall-pressure propagation speed.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 55
- Cited by

