Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sandham, Neil D.
2016.
Effects of Compressibility and Shock-Wave Interactions on Turbulent Shear Flows.
Flow, Turbulence and Combustion,
Vol. 97,
Issue. 1,
p.
1.
Grossman, Ilan J.
and
Bruce, Paul J.
2017.
Effect of Test Article Geometry on Shock Wave-Boundary Layer Interactions in Rectangular Intakes.
Pasquariello, Vito
Hickel, Stefan
and
Adams, Nikolaus A.
2017.
Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
617.
Grossman, Ilan J.
and
Bruce, Paul J. K.
2018.
Confinement effects on regular–irregular transition in shock-wave–boundary-layer interactions.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
171.
Volpiani, Pedro S.
Bernardini, Matteo
and
Larsson, Johan
2018.
Effects of a nonadiabatic wall on supersonic shock/boundary-layer interactions.
Physical Review Fluids,
Vol. 3,
Issue. 8,
Yu, Xin
Huang, Xiao
and
Zheng, Miao
2018.
Effects of Different Equations of State on the Oblique Shock Wave Reflection in Solids.
Procedia Structural Integrity,
Vol. 13,
Issue. ,
p.
1037.
Hu, Weibo
Hickel, Stefan
and
van Oudheusden, Bas
2019.
Dynamics of a supersonic transitional flow over a backward-facing step.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Zuo, Feng-Yuan
and
Memmolo, Antonio
2020.
Investigation of conical shock wave/boundary layer interaction in axisymmetric internal flow.
Aerospace Science and Technology,
Vol. 106,
Issue. ,
p.
106106.
Laguarda, L.
Hickel, S.
Schrijer, F. F. J.
and
van Oudheusden, B. W.
2020.
Dynamics of unsteady asymmetric shock interactions.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Volpiani, Pedro S.
Bernardini, Matteo
and
Larsson, Johan
2020.
Effects of a nonadiabatic wall on hypersonic shock/boundary-layer interactions.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Hu, Weibo
Hickel, Stefan
and
van Oudheusden, Bas
2020.
Influence of upstream disturbances on the primary and secondary instabilities in a supersonic separated flow over a backward-facing step.
Physics of Fluids,
Vol. 32,
Issue. 5,
Xue, Longsheng
Schrijer, Ferry F. J.
van Oudheusden, Bas W.
Wang, Chengpeng
Shi, Zhiwei
and
Cheng, Keming
2020.
Theoretical study on regular reflection of shock wave–boundary layer interactions.
Journal of Fluid Mechanics,
Vol. 899,
Issue. ,
Li, Xin
Tan, Hui-jun
Zhang, Yue
Huang, He-xia
Guo, Yun-jie
and
Lin, Zheng-kang
2020.
Flow patterns of dual-incident shock waves/turbulent boundary layer interaction.
Journal of Visualization,
Vol. 23,
Issue. 6,
p.
931.
Xie, Wen-Zhong
Yang, Shu-Zi
Zeng, Cheng
Liao, Kai
Ding, Run-Han
Zhang, Lu
and
Guo, Shengmin
2021.
Improvement of the free-interaction theory for shock wave/turbulent boundary layer interactions.
Physics of Fluids,
Vol. 33,
Issue. 7,
Karabelas, S. J.
and
Markatos, N.C.
2021.
Unsteady Transition From a Mach to a Regular Shockwave Intersection.
WSEAS TRANSACTIONS ON HEAT AND MASS TRANSFER,
Vol. 16,
Issue. ,
p.
153.
Xue, Longsheng
Wang, Chengpeng
and
Cheng, Keming
2021.
A study on the RR-to-MR transition of shock wave reflections near the leading edge in hypersonic flows.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Wang, Miao-Miao
and
Wu, Zi-Niu
2021.
Transition study for asymmetric reflection between moving incident shock waves.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Martínez-Ruiz, D.
Huete, C.
Martínez-Ferrer, P. J.
and
Mira, D.
2021.
Specific heat effects in two-dimensional shock refractions.
Shock Waves,
Vol. 31,
Issue. 1,
p.
1.
Li, Nan
Chang, Juntao
Xu, Kejing
Yu, Daren
and
Bao, Wen
2021.
Instability of shock train behaviour with incident shocks.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
Laguarda, L.
Santiago Patterson, J.
Schrijer, F. F. J.
van Oudheusden, B. W.
and
Hickel, S.
2021.
Experimental investigation of shock–shock interactions with variable inflow Mach number.
Shock Waves,
Vol. 31,
Issue. 5,
p.
457.
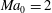 $\mathit{Ma}_{0}=2$ . Computational results show that the mean deflection angle across the separation shock is decoupled from the incident shock wave and can be accurately modelled by the generalised free interaction theory. On the basis of these observations, and the von Neumann and detachment criteria for the asymmetric intersection of shock waves, we derive the critical incident shock deflection angles at which the shock pattern may/must become irregular. Numerical data for a free-stream Mach number of
$\mathit{Ma}_{0}=2$ . Computational results show that the mean deflection angle across the separation shock is decoupled from the incident shock wave and can be accurately modelled by the generalised free interaction theory. On the basis of these observations, and the von Neumann and detachment criteria for the asymmetric intersection of shock waves, we derive the critical incident shock deflection angles at which the shock pattern may/must become irregular. Numerical data for a free-stream Mach number of 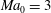 $\mathit{Ma}_{0}=3$ confirm the existence of the dual-solution domain predicted by theory.
$\mathit{Ma}_{0}=3$ confirm the existence of the dual-solution domain predicted by theory.

