1. Introduction
Grid turbulence has been investigated for a long time owing to its good approximation to homogeneous and isotropic turbulence. In the classic flow configuration, a planar grid or screen with uniform mesh size and definite rod thickness is held in a uniform fluid stream. Downstream of the grid, homogeneity is achieved on cross-flow planes and a degree of isotropy is exhibited. This canonical flow has assumed an essential role in understanding turbulence and has allowed the formulation and testing of theories and models since the early wind tunnel experiments (Simmons & Salter Reference Simmons and Salter1934; Taylor Reference Taylor1935).
The search for self-preserving or self-similar forms of correlation or spectral functions has led to the theories of homogeneous isotropic turbulence proposed over the past decades and the common prediction that turbulence decays according to a power law (de Karman & Howarth Reference de Karman and Howarth1938; Kolmogorov Reference Kolmogorov1941; Batchelor Reference Batchelor1948; Saffman Reference Saffman1967; George Reference George1992). Despite the fact that these theories agree on the form, the value of the decay exponent ![]() $n$ is still debated. The theoretical analyses by de Karman & Howarth (Reference de Karman and Howarth1938), Batchelor (Reference Batchelor1948) and Saffman (Reference Saffman1967) resulted in values for
$n$ is still debated. The theoretical analyses by de Karman & Howarth (Reference de Karman and Howarth1938), Batchelor (Reference Batchelor1948) and Saffman (Reference Saffman1967) resulted in values for ![]() $n$ of
$n$ of ![]() $1$,
$1$, ![]() $10/7$ and
$10/7$ and ![]() $6/5$, respectively. A large collection of experimental measurements involving classical grids of various geometries and at different flow regimes has grown up over the years. While the earliest works supported the prediction that
$6/5$, respectively. A large collection of experimental measurements involving classical grids of various geometries and at different flow regimes has grown up over the years. While the earliest works supported the prediction that ![]() $n = 1$ (Batchelor & Townsend Reference Batchelor and Townsend1948), later experiments by Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1966) and Mohamed & Larue (Reference Mohamed and Larue1990) corrected the decay exponent, with values falling between
$n = 1$ (Batchelor & Townsend Reference Batchelor and Townsend1948), later experiments by Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1966) and Mohamed & Larue (Reference Mohamed and Larue1990) corrected the decay exponent, with values falling between ![]() $1.1$ and
$1.1$ and ![]() $1.4$ (Lavoie, Djenidi & Antonia Reference Lavoie, Djenidi and Antonia2007; Kurian & Fransson Reference Kurian and Fransson2009; Kitamura et al. Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014, and references therein). George (Reference George1992) argued that the apparent discrepancies in the measurements are related to an undefined dependence of the flow on the initial conditions. This precludes the existence of a single universal state, at least at finite Reynolds number. Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) investigated the effects of the initial conditions on the characteristics of decaying turbulence, and showed that this impact is more marked as the anisotropy and the strength of large-scale periodic motions increase. On the other hand, the improvement of isotropy and of large-scale periodic character reduces the influence of initial conditions. This suggested that the dependence on initial conditions is associated with departures from ideal homogeneity and isotropy conditions.
$1.4$ (Lavoie, Djenidi & Antonia Reference Lavoie, Djenidi and Antonia2007; Kurian & Fransson Reference Kurian and Fransson2009; Kitamura et al. Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014, and references therein). George (Reference George1992) argued that the apparent discrepancies in the measurements are related to an undefined dependence of the flow on the initial conditions. This precludes the existence of a single universal state, at least at finite Reynolds number. Lavoie et al. (Reference Lavoie, Djenidi and Antonia2007) investigated the effects of the initial conditions on the characteristics of decaying turbulence, and showed that this impact is more marked as the anisotropy and the strength of large-scale periodic motions increase. On the other hand, the improvement of isotropy and of large-scale periodic character reduces the influence of initial conditions. This suggested that the dependence on initial conditions is associated with departures from ideal homogeneity and isotropy conditions.
Recent research has attempted to reconcile many of the experimental data with Saffman turbulence. According to these analyses, the value ![]() $n = 6/5$ represents a minimum decay rate valid for (strictly) homogeneous turbulence and which could also have deviations because of an inhomogeneous decay. The large-scale turbulent structures are proven to be regulated by the invariance of the Saffman integral. This is physically interpreted as the conservation of linear momentum and is opposed to the invariance of the Loitsyansky integral, on which Batchelor turbulence is based. It is concluded in the work by Krogstad & Davidson (Reference Krogstad and Davidson2010) that ‘it seems very likely’ that the turbulence observed is Saffman turbulence, and that it is also possible that different grid geometries, or other ranges of
$n = 6/5$ represents a minimum decay rate valid for (strictly) homogeneous turbulence and which could also have deviations because of an inhomogeneous decay. The large-scale turbulent structures are proven to be regulated by the invariance of the Saffman integral. This is physically interpreted as the conservation of linear momentum and is opposed to the invariance of the Loitsyansky integral, on which Batchelor turbulence is based. It is concluded in the work by Krogstad & Davidson (Reference Krogstad and Davidson2010) that ‘it seems very likely’ that the turbulence observed is Saffman turbulence, and that it is also possible that different grid geometries, or other ranges of ![]() ${\textit {Re}}$, could produce different results. Also Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014) report that grid turbulence is of Saffman type for the Reynolds-number range examined in their work, when grid turbulence is generated by a square or a cylindrical grid.
${\textit {Re}}$, could produce different results. Also Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014) report that grid turbulence is of Saffman type for the Reynolds-number range examined in their work, when grid turbulence is generated by a square or a cylindrical grid.
Aside from the existence of a self-preserving solution, Mohamed & Larue (Reference Mohamed and Larue1990) attributed the difficulty in finding a single decay exponent also to inconsistencies in the data analysis method. In particular, the inaccuracy is related to the uncertainty in the virtual origin and the inclusion of data pertaining to the inhomogeneous and anisotropic region in the developed range. For grid turbulence, the turbulence decay is to be evaluated starting from ![]() $x/M > 40\text {--}60$, where
$x/M > 40\text {--}60$, where ![]() $x$ is the distance from the grid and
$x$ is the distance from the grid and ![]() $M$ is the mesh width.
$M$ is the mesh width.
A class of turbulence-generating grid consisting of fractal geometries has been introduced starting from the work by Hurst & Vassilicos (Reference Hurst and Vassilicos2007). Since then, fractal grids have attracted a lot of interest because of the specific type of turbulence generated. A remarkable increase in the Reynolds number based on the Taylor scale with respect to usual passive grids was noticed by Seoud & Vassilicos (Reference Seoud and Vassilicos2007). Further studies investigating the decaying turbulence downstream of a set of multiscale grids (Krogstad & Davidson Reference Krogstad and Davidson2012) and a square-element fractal grid (Hearst & Lavoie Reference Hearst and Lavoie2014) have revealed that, while the region close to the grids can be characterised by residual inhomogeneity and is grid-dependent, in the far field – where development is accomplished – flow characteristics are in accordance with classical grid turbulence measurements.
The in-depth study of turbulence generated by fractal grids has revealed a peculiar behaviour of the dissipation coefficient ![]() $C_\epsilon = \langle \epsilon \rangle L / u^3$ (here
$C_\epsilon = \langle \epsilon \rangle L / u^3$ (here ![]() $\langle \epsilon \rangle$ is the rate of dissipation.) in a region close to the turbulence-generating grid but in conjunction with energy spectra, which follow the
$\langle \epsilon \rangle$ is the rate of dissipation.) in a region close to the turbulence-generating grid but in conjunction with energy spectra, which follow the ![]() $-5/3$ slope for a wide range of wavenumbers. This behaviour has been described as a breakdown of the classical dissipation scaling and is observed in wind tunnel experiments of grid-generated turbulence of different geometries (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Isaza, Salazar & Warhaft Reference Isaza, Salazar and Warhaft2014; Valente & Vassilicos Reference Valente and Vassilicos2014; Mora et al. Reference Mora, Muñiz Pladellorens, Riera Turró, Lagauzere and Obligado2019) and also in direct numerical simulation (DNS) data of decaying turbulence in a periodic box (Goto & Vassilicos Reference Goto and Vassilicos2016). The breakdown consists in a behaviour of
$-5/3$ slope for a wide range of wavenumbers. This behaviour has been described as a breakdown of the classical dissipation scaling and is observed in wind tunnel experiments of grid-generated turbulence of different geometries (Mazellier & Vassilicos Reference Mazellier and Vassilicos2010; Isaza, Salazar & Warhaft Reference Isaza, Salazar and Warhaft2014; Valente & Vassilicos Reference Valente and Vassilicos2014; Mora et al. Reference Mora, Muñiz Pladellorens, Riera Turró, Lagauzere and Obligado2019) and also in direct numerical simulation (DNS) data of decaying turbulence in a periodic box (Goto & Vassilicos Reference Goto and Vassilicos2016). The breakdown consists in a behaviour of ![]() $C_{\epsilon }$ at the initial stages of the decay that depends upon the inlet Reynolds number
$C_{\epsilon }$ at the initial stages of the decay that depends upon the inlet Reynolds number ![]() ${\textit {Re}}_{M}$ and the local Reynolds number
${\textit {Re}}_{M}$ and the local Reynolds number ![]() ${\textit {Re}}_{\lambda }$ as follows:
${\textit {Re}}_{\lambda }$ as follows: ![]() $C_{\epsilon } \sim {\textit {Re}}_{M}^{1/2}/{\textit {Re}}_{\lambda }$. This implies that
$C_{\epsilon } \sim {\textit {Re}}_{M}^{1/2}/{\textit {Re}}_{\lambda }$. This implies that ![]() $L/\lambda \sim {\textit {Re}}_{M}^{1/2}$ along the direction of
$L/\lambda \sim {\textit {Re}}_{M}^{1/2}$ along the direction of ![]() ${\textit {Re}}_{\lambda }$ decay (Valente & Vassilicos Reference Valente and Vassilicos2012).
${\textit {Re}}_{\lambda }$ decay (Valente & Vassilicos Reference Valente and Vassilicos2012).
The turbulent flow behind an open-cell metal foam has never been investigated before. Similar to regular grids, the open-cell metal foam geometry is characterised by two main length scales, i.e. the mean pore diameter ![]() $d_p$ and the mean ligament thickness
$d_p$ and the mean ligament thickness ![]() $d_f$. In contrast to regular grids, open cells are arranged randomly in space and their morphology, based on a polyhedral frame, is never exactly repeated. This generates a structure that is highly irregular and anisotropic at the pore scale but statistically isotropic at the macroscale. In addition, the metal foam layer investigated here has a thickness larger than a single ligament or a pore. Moreover, the solidity of metal foams, measured as
$d_f$. In contrast to regular grids, open cells are arranged randomly in space and their morphology, based on a polyhedral frame, is never exactly repeated. This generates a structure that is highly irregular and anisotropic at the pore scale but statistically isotropic at the macroscale. In addition, the metal foam layer investigated here has a thickness larger than a single ligament or a pore. Moreover, the solidity of metal foams, measured as ![]() $1-\varepsilon$, where
$1-\varepsilon$, where ![]() $\varepsilon$ represents grid porosity, is very different from the solidities typical of grids employed for grid turbulence, which generally range between
$\varepsilon$ represents grid porosity, is very different from the solidities typical of grids employed for grid turbulence, which generally range between ![]() $0.30$ and
$0.30$ and ![]() $0.45$. In high-porosity metal foams, this value is typically lower than
$0.45$. In high-porosity metal foams, this value is typically lower than ![]() $0.10$ (Calmidi & Mahajan Reference Calmidi and Mahajan2000).
$0.10$ (Calmidi & Mahajan Reference Calmidi and Mahajan2000).
In this paper, a description is reported of turbulence downstream of a high-porosity open-cell metal foam. After a qualitative introduction to the flow investigated in § 3.1, the degree of homogeneity and isotropy of turbulence is investigated in § 3.2. The power-law behaviour of turbulent kinetic energy ![]() $\langle k \rangle$ and its dissipation rate are assessed in § 3.3 and § 3.4, respectively. The streamwise variations of turbulent length scales are considered in § 3.5. In § 3.6 the behaviour of the dissipation rate coefficient is investigated in detail, also in the context of recent research on the topic. In § 3.7 the discussion is about whether or not Saffman turbulence is achieved for the present flow configuration. The multiscale nature of the flow is examined by means of one-dimensional spectra in § 3.8. Then § 3.9 investigates high-order statistics, the role of intermittency and the decorrelation length of dissipation. Budget terms of turbulent kinetic energy and of velocity variances are reported in § 3.10, where the main mechanisms for the transport of energy and fluctuations are described in the vicinity of the solid structure and in the fully developed region. Final remarks are drawn in § 4.
$\langle k \rangle$ and its dissipation rate are assessed in § 3.3 and § 3.4, respectively. The streamwise variations of turbulent length scales are considered in § 3.5. In § 3.6 the behaviour of the dissipation rate coefficient is investigated in detail, also in the context of recent research on the topic. In § 3.7 the discussion is about whether or not Saffman turbulence is achieved for the present flow configuration. The multiscale nature of the flow is examined by means of one-dimensional spectra in § 3.8. Then § 3.9 investigates high-order statistics, the role of intermittency and the decorrelation length of dissipation. Budget terms of turbulent kinetic energy and of velocity variances are reported in § 3.10, where the main mechanisms for the transport of energy and fluctuations are described in the vicinity of the solid structure and in the fully developed region. Final remarks are drawn in § 4.
2. Numerical methodology
2.1. Mathematical formulation and flow configuration
The system of equations solved numerically comprises the mass conservation and the Navier–Stokes equations for incompressible flows:
 \begin{align} \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\partial U_i}{\partial x_i} = 0, \\ \displaystyle \dfrac{\partial U_i}{\partial t} + \dfrac{\partial U_i U_j}{\partial x_j} = \displaystyle -\dfrac{\partial P}{\partial x_i} + \dfrac{1}{{\textit{Re}}_{d_p}} \dfrac{\partial^2 U_i}{\partial x_j \partial x_j}, \end{array}\right. \end{align}
\begin{align} \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\partial U_i}{\partial x_i} = 0, \\ \displaystyle \dfrac{\partial U_i}{\partial t} + \dfrac{\partial U_i U_j}{\partial x_j} = \displaystyle -\dfrac{\partial P}{\partial x_i} + \dfrac{1}{{\textit{Re}}_{d_p}} \dfrac{\partial^2 U_i}{\partial x_j \partial x_j}, \end{array}\right. \end{align}
complemented with appropriate boundary conditions. The subscripts ![]() $i$ and
$i$ and ![]() $j$ take the values
$j$ take the values ![]() $1$,
$1$, ![]() $2$ and
$2$ and ![]() $3$ to denote the streamwise direction,
$3$ to denote the streamwise direction, ![]() $x$, and the two cross-flow directions,
$x$, and the two cross-flow directions, ![]() $y$ and
$y$ and ![]() $z$, respectively. All the variables are made non-dimensional by the velocity at the inlet
$z$, respectively. All the variables are made non-dimensional by the velocity at the inlet ![]() $U_\infty$ and the mean pore diameter of the metal foam
$U_\infty$ and the mean pore diameter of the metal foam ![]() $d_p$. The Reynolds number based on the unperturbed velocity and the mean pore diameter is
$d_p$. The Reynolds number based on the unperturbed velocity and the mean pore diameter is ![]() ${\textit {Re}}_{d_p} = 4000$.
${\textit {Re}}_{d_p} = 4000$.
The governing equations (2.1) are solved using the high-order finite-difference method implemented in Incompact3d (Laizet & Lamballais Reference Laizet and Lamballais2009). Sixth-order compact schemes are used for spatial discretisation (Lele Reference Lele1992), and time integration is done by the third-order Adams–Bashforth scheme. The velocity field is evaluated on a Cartesian grid with uniform spacing along the three directions, and pressure is defined on a staggered grid. Pressure–velocity decoupling is accomplished by a fractional-step method, which determines the divergence-free velocity field by solving a Poisson equation. The Poisson problem is tackled in the spectral space by using a modified wavenumber formalism, which allows for any kind of boundary conditions for the velocity field in the physical space. Inflow/outflow boundary conditions are enforced along the streamwise direction and periodic boundary conditions are set along the cross-flow directions to represent statistical homogeneity. A uniform velocity field is prescribed at the inlet ![]() $(U_\infty , 0, 0 )$, while at the outlet the velocity is determined by a convection equation:
$(U_\infty , 0, 0 )$, while at the outlet the velocity is determined by a convection equation:
The convection velocity ![]() $c$ is calculated at each time step as the mean between the maximum and minimum values of the streamwise velocity component at the outlet.
$c$ is calculated at each time step as the mean between the maximum and minimum values of the streamwise velocity component at the outlet.
The representation of the intricate metal foam geometry is achieved via an immersed boundary method (IBM) based on direct forcing (Gautier, Laizet & Lamballais Reference Gautier, Laizet and Lamballais2014). The IBM enforces the no-slip condition at the solid walls while preserving the simplicity of the finite-difference schemes applied to the Cartesian grid (Laizet & Lamballais Reference Laizet and Lamballais2009). Further details on the numerical methodology employed here are provided in Corsini & Stalio (Reference Corsini and Stalio2020).
A sketch of the computational domain is displayed in figure 1. The extents of the domain along the streamwise and the two cross-flow directions are ![]() $L_x = 45d_p$ and
$L_x = 45d_p$ and ![]() $L_y = L_z = 11.25d_p$, respectively. The origin of the coordinate system is located at the centre of the downstream face of the porous matrix; thus
$L_y = L_z = 11.25d_p$, respectively. The origin of the coordinate system is located at the centre of the downstream face of the porous matrix; thus ![]() $x = 0$ describes the most upstream cross-flow plane where the fluid is not in contact with the solid phase. The thickness of the metal foam layer in the streamwise direction is
$x = 0$ describes the most upstream cross-flow plane where the fluid is not in contact with the solid phase. The thickness of the metal foam layer in the streamwise direction is ![]() $5d_p$ and it spans the whole domain in the cross-flow directions. It is placed at a
$5d_p$ and it spans the whole domain in the cross-flow directions. It is placed at a ![]() $5d_p$ distance from the inlet section; this avoids interference between the upstream boundary and the solid matrix.
$5d_p$ distance from the inlet section; this avoids interference between the upstream boundary and the solid matrix.

Figure 1. Schematic representation of the computational domain.
The computational domain is discretised by ![]() $n_x = 3073$ grid nodes in the streamwise direction and
$n_x = 3073$ grid nodes in the streamwise direction and ![]() $n_y = n_z = 768$ in the cross-flow directions. The spatial resolution is sufficiently fine to ensure that
$n_y = n_z = 768$ in the cross-flow directions. The spatial resolution is sufficiently fine to ensure that ![]() $\Delta x = \Delta y = \Delta z \leqslant 2 \eta$ for
$\Delta x = \Delta y = \Delta z \leqslant 2 \eta$ for ![]() $x \geqslant 5$. Close to the porous layer (
$x \geqslant 5$. Close to the porous layer (![]() $0 < x < 5$), where dissipation is larger,
$0 < x < 5$), where dissipation is larger, ![]() $\Delta x = \Delta y = \Delta z \leqslant 5 \eta$. In the above comparisons, the Kolmogorov microscale
$\Delta x = \Delta y = \Delta z \leqslant 5 \eta$. In the above comparisons, the Kolmogorov microscale ![]() $\eta$ is calculated a posteriori from its definition. The time step is kept at
$\eta$ is calculated a posteriori from its definition. The time step is kept at ![]() $\Delta t= 0.001 d_{p}/U_{\infty }$ during the simulation, which in terms of the Kolmogorov time scale
$\Delta t= 0.001 d_{p}/U_{\infty }$ during the simulation, which in terms of the Kolmogorov time scale ![]() $\tau _{\eta }$ yields
$\tau _{\eta }$ yields ![]() $\Delta t \leqslant 0.033 \tau _{\eta }$. This corresponds to a Courant–Friedrichs–Lewy number
$\Delta t \leqslant 0.033 \tau _{\eta }$. This corresponds to a Courant–Friedrichs–Lewy number ![]() ${CFL}<0.3$.
${CFL}<0.3$.
Statistical quantities are computed by averaging in time and along the homogeneous ![]() $y$ and
$y$ and ![]() $z$ directions. Gathering of statistics begins after one flow-through time from the start of the simulation. In order to obtain well-converged statistics, the time interval of collection is
$z$ directions. Gathering of statistics begins after one flow-through time from the start of the simulation. In order to obtain well-converged statistics, the time interval of collection is ![]() $T = 225 d_{p}/U_{\infty }$, and the three-dimensional snapshots of the velocity and pressure field are sampled at equal time intervals of
$T = 225 d_{p}/U_{\infty }$, and the three-dimensional snapshots of the velocity and pressure field are sampled at equal time intervals of ![]() $\Delta T = 4.5 d_{p}/U_{\infty }$.
$\Delta T = 4.5 d_{p}/U_{\infty }$.
2.2. Metal foam geometry
The problem of the computer modelling of an intricate metal foam porous structure has been tackled in different ways. Pore-scale morphology can be reconstructed through X-ray tomography (Piller et al. Reference Piller, Boschetto, Stalio, Schena and Errico2013) or generated mathematically assuming an ideal cell geometry based on a virtual sample of regular polyhedra (Boomsma, Poulikakos & Ventikos Reference Boomsma, Poulikakos and Ventikos2003). In this study, where geometric periodicity is a key feature of the numerical representation and irregularity of the foam is a requirement, a third approach is adopted: the open-pore cellular structure is generated synthetically through a numerical algorithm, developed by August et al. (Reference August, Ettrich, Rölle, Schmid, Berghoff, Selzer and Nestler2015). Besides the excellent realism and periodicity, one further favourable feature of synthetic metal foams is the possibility to tune their porosity and permeability. Thanks to a diffuse interface representation of the phase-field approach (August et al. Reference August, Ettrich, Rölle, Schmid, Berghoff, Selzer and Nestler2015), the thickness of ligaments can be easily adjusted. Figure 2 shows the details of a couple of cells of the synthetic structure.

Figure 2. Cells of the aluminium foam generated algorithmically (August et al. Reference August, Ettrich, Rölle, Schmid, Berghoff, Selzer and Nestler2015).
The synthetic metal foam structure used in the simulation is characterised by the geometrical features listed in table 1. Both ![]() $d_p$ and
$d_p$ and ![]() $d_f$ are calculated by spatial averages and thus represent the mean pore diameter and the mean ligament thickness of the metal foam sample. The value of grid porosity set,
$d_f$ are calculated by spatial averages and thus represent the mean pore diameter and the mean ligament thickness of the metal foam sample. The value of grid porosity set, ![]() $\varepsilon = 0.92$, is representative of high-porosity metal foams (Calmidi & Mahajan Reference Calmidi and Mahajan2000). Based on typical sizes of open-cell aluminium foams, an inflow velocity of
$\varepsilon = 0.92$, is representative of high-porosity metal foams (Calmidi & Mahajan Reference Calmidi and Mahajan2000). Based on typical sizes of open-cell aluminium foams, an inflow velocity of ![]() $U_{\infty } = 15\ \textrm {m}\ \textrm {s}^{-1}$ is obtained at
$U_{\infty } = 15\ \textrm {m}\ \textrm {s}^{-1}$ is obtained at ![]() ${\textit {Re}}_{d_p} = 4000$, assuming air at standard conditions as the working fluid. Table 1 reports experimental conditions from previous wind tunnel studies on regular planar grids.
${\textit {Re}}_{d_p} = 4000$, assuming air at standard conditions as the working fluid. Table 1 reports experimental conditions from previous wind tunnel studies on regular planar grids.
Table 1. Outline of flow parameters, decay exponent ![]() $n$ and length scales of turbulence generated by the open-cell metal foam. The experimental results of Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971), Kurian & Fransson (Reference Kurian and Fransson2009), Krogstad & Davidson (Reference Krogstad and Davidson2010) and Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014) on the turbulence generated by regular grids are also included. Here
$n$ and length scales of turbulence generated by the open-cell metal foam. The experimental results of Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971), Kurian & Fransson (Reference Kurian and Fransson2009), Krogstad & Davidson (Reference Krogstad and Davidson2010) and Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014) on the turbulence generated by regular grids are also included. Here ![]() $M$,
$M$, ![]() $d$ and
$d$ and ![]() $\sigma$ denote the mesh width, the rod thickness and the solidity of the grid, respectively. Asterisk
$\sigma$ denote the mesh width, the rod thickness and the solidity of the grid, respectively. Asterisk ![]() $^*$ denotes quantities expressed in dimensional form. Quantities in parentheses indicate values that have been deduced from other quantities provided in the same work.
$^*$ denotes quantities expressed in dimensional form. Quantities in parentheses indicate values that have been deduced from other quantities provided in the same work.

A sample of the metal foam geometry with superimposed computational points is displayed in figure 2 of Corsini & Stalio (Reference Corsini and Stalio2020). Staircase patterns of the immersed boundaries approximate the rounded borders of the solid region. This referenced picture and the computed ratio between average ligament diameter and grid spacing ![]() $d_f/\Delta x \approx 10$ suggest that the ligaments are discretised by an adequate number of grid points.
$d_f/\Delta x \approx 10$ suggest that the ligaments are discretised by an adequate number of grid points.
3. Results and discussion
3.1. Instantaneous and mean flows
Figure 3(a) shows the streamwise component of the instantaneous velocity field in one of the snapshots collected. The uniform free stream of the inflow is disrupted by the irregularly arranged ligaments of the solid structure and velocity fluctuations arise within the porous matrix. Vortices of different orientations are shed from the ligaments and a wake is formed. The largest perturbations are observed close to the downstream edge of the porous matrix. The wakes originated by the ligaments develop in a non-uniform fashion and interact at variable lengths. The smaller wakes are seen to disappear after a couple of pore diameters, whereas larger wakes stemming from ligament clumps meet at a further distance from the foam. The larger wakes also last in time, as revealed by the streaks in the time-averaged velocity field ![]() $\langle U \rangle _t$ shown in figure 3(b).
$\langle U \rangle _t$ shown in figure 3(b).

Figure 3. Instantaneous velocity field of the streamwise velocity component (a) and its temporal mean (b) in an ![]() $x$–
$x$–![]() $y$ plane.
$y$ plane.
3.2. Homogeneity and isotropy
The approximation to statistical homogeneity in the cross-flow directions in grid turbulence is known to depend on the grid geometry and the Reynolds number. While, for regular grids, experiments suggest that the flow becomes nearly homogeneous for ![]() $x/M > 40$ (Comte-Bellot & Corrsin Reference Comte-Bellot and Corrsin1966; Mohamed & Larue Reference Mohamed and Larue1990), for fractal grids, homogeneity is usually retrieved further downstream (Hearst & Lavoie Reference Hearst and Lavoie2014) and, for example, Valente & Vassilicos (Reference Valente and Vassilicos2011) report
$x/M > 40$ (Comte-Bellot & Corrsin Reference Comte-Bellot and Corrsin1966; Mohamed & Larue Reference Mohamed and Larue1990), for fractal grids, homogeneity is usually retrieved further downstream (Hearst & Lavoie Reference Hearst and Lavoie2014) and, for example, Valente & Vassilicos (Reference Valente and Vassilicos2011) report ![]() $x/M_{{eff}}>80$, where
$x/M_{{eff}}>80$, where ![]() $M_{{eff}}$ is the effective mesh size.
$M_{{eff}}$ is the effective mesh size.
The distribution of ![]() $\langle U \rangle _t$ in cross-flow planes is shown in figure 4 for six streamwise positions at increasing distance from the metal foam. Solid lines mark regions where the percentage of variation of
$\langle U \rangle _t$ in cross-flow planes is shown in figure 4 for six streamwise positions at increasing distance from the metal foam. Solid lines mark regions where the percentage of variation of ![]() $\langle U \rangle _t$ relative to
$\langle U \rangle _t$ relative to ![]() $U_{\infty }$ has magnitude greater than
$U_{\infty }$ has magnitude greater than ![]() $10\,\%$, while dashed lines encompass regions of magnitude greater than
$10\,\%$, while dashed lines encompass regions of magnitude greater than ![]() $5\,\%$. These are seen to gradually shrink along
$5\,\%$. These are seen to gradually shrink along ![]() $x$. While inhomogeneity is in part to be ascribed to the limited size of the sample composed only by the collection of snapshots in time, for
$x$. While inhomogeneity is in part to be ascribed to the limited size of the sample composed only by the collection of snapshots in time, for ![]() $x > 20$ their extent is still appreciable. In the
$x > 20$ their extent is still appreciable. In the ![]() $x = 30$ station, the time-averaged velocity
$x = 30$ station, the time-averaged velocity ![]() $\langle U \rangle _t$ varies between
$\langle U \rangle _t$ varies between ![]() $0.86$ and
$0.86$ and ![]() $1.12$.
$1.12$.

Figure 4. Streamwise mean flow field ![]() $\langle U \rangle _t$ in
$\langle U \rangle _t$ in ![]() $y$–
$y$–![]() $z$ planes extracted at
$z$ planes extracted at ![]() $x=5$,
$x=5$, ![]() $10$,
$10$, ![]() $15$,
$15$, ![]() $20$,
$20$, ![]() $25$ and
$25$ and ![]() $30$ (left to right then top to bottom): solid line, isolines
$30$ (left to right then top to bottom): solid line, isolines ![]() $\langle U \rangle _t - U_{\infty } = \pm 0.1$; and dashed line, isolines
$\langle U \rangle _t - U_{\infty } = \pm 0.1$; and dashed line, isolines ![]() $\langle U \rangle _t - U_{\infty } = \pm 0.05$.
$\langle U \rangle _t - U_{\infty } = \pm 0.05$.
The isotropy level of the large scales of motion can be investigated through the ratio of root-mean-square (r.m.s.) velocity fluctuations along orthogonal directions. In the present case, the fluctuations of the ![]() $x$-component of velocity are the largest: in the developed region, indicators
$x$-component of velocity are the largest: in the developed region, indicators ![]() $u_{rms}/w_{rms}$ and
$u_{rms}/w_{rms}$ and ![]() $u_{rms}/v_{rms}$ oscillate within the interval
$u_{rms}/v_{rms}$ oscillate within the interval ![]() $(1.5, 1.6)$ about a mean of 1.55 for
$(1.5, 1.6)$ about a mean of 1.55 for ![]() $u_{rms}/v_{rms}$ and 1.56 for
$u_{rms}/v_{rms}$ and 1.56 for ![]() $u_{rms}/w_{rms}$, where the difference is finally due to the size of the sample employed in the simulations. In previous grid turbulence measurements (Kurian & Fransson Reference Kurian and Fransson2009; Krogstad & Davidson Reference Krogstad and Davidson2010; Kitamura et al. Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014), the observed isotropy indicators are in general smaller than those measured here. Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014), who also collected experimental results by other authors, report
$u_{rms}/w_{rms}$, where the difference is finally due to the size of the sample employed in the simulations. In previous grid turbulence measurements (Kurian & Fransson Reference Kurian and Fransson2009; Krogstad & Davidson Reference Krogstad and Davidson2010; Kitamura et al. Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014), the observed isotropy indicators are in general smaller than those measured here. Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014), who also collected experimental results by other authors, report ![]() $u_{rms}/w_{rms} < 1.2$ in all cases; similar values are also reported in the lee of fractal grids (Hurst & Vassilicos Reference Hurst and Vassilicos2007; Gomes-Fernandes, Ganapathisubramani & Vassilicos Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012). More details about large-scale isotropy measures downstream of the present metal foam are reported in Corsini & Stalio (Reference Corsini and Stalio2020).
$u_{rms}/w_{rms} < 1.2$ in all cases; similar values are also reported in the lee of fractal grids (Hurst & Vassilicos Reference Hurst and Vassilicos2007; Gomes-Fernandes, Ganapathisubramani & Vassilicos Reference Gomes-Fernandes, Ganapathisubramani and Vassilicos2012). More details about large-scale isotropy measures downstream of the present metal foam are reported in Corsini & Stalio (Reference Corsini and Stalio2020).
3.3. Decay of velocity fluctuations
Figure 5 displays the streamwise evolution of the variance of the three components of velocity ![]() $\langle u_i u_i\rangle$ as well as the turbulent kinetic energy
$\langle u_i u_i\rangle$ as well as the turbulent kinetic energy ![]() $\langle k \rangle$. Very close to the foam and for
$\langle k \rangle$. Very close to the foam and for ![]() $x < 1$, velocity fluctuations are observed to remain constant. The negative slope increases gradually in
$x < 1$, velocity fluctuations are observed to remain constant. The negative slope increases gradually in ![]() $x$ until fluctuations exhibit a power-law decay that persists until the end of the computational domain. As demonstrated, for example, in Tennekes & Lumley (Reference Tennekes and Lumley1972), this is expected in the region where advection and dissipation of the turbulent kinetic energy become the only non-negligible terms in the transport equation of
$x$ until fluctuations exhibit a power-law decay that persists until the end of the computational domain. As demonstrated, for example, in Tennekes & Lumley (Reference Tennekes and Lumley1972), this is expected in the region where advection and dissipation of the turbulent kinetic energy become the only non-negligible terms in the transport equation of ![]() $\langle k \rangle$; see § 3.10.
$\langle k \rangle$; see § 3.10.

Figure 5. Decay of velocity fluctuations: solid line, ![]() $\langle uu\rangle$; dot-dashed line,
$\langle uu\rangle$; dot-dashed line, ![]() $\langle vv\rangle$; dotted line,
$\langle vv\rangle$; dotted line, ![]() $\langle ww\rangle$; and dashed line,
$\langle ww\rangle$; and dashed line, ![]() $\langle k \rangle$.
$\langle k \rangle$.
Power-law parameters are sought in the form
through a numerical procedure. In (3.1), ![]() $A$ is the multiplicative coefficient,
$A$ is the multiplicative coefficient, ![]() $x_0$ is the virtual origin and
$x_0$ is the virtual origin and ![]() $n$ is the decay exponent. As
$n$ is the decay exponent. As ![]() $n$ is positive, the power law has a vertical asymptote (and a singularity) at the virtual origin
$n$ is positive, the power law has a vertical asymptote (and a singularity) at the virtual origin ![]() $x = x_0$. As the parameters in (3.1) depend greatly upon the interval of sampling data considered, also the interval limits are determined inside the fitting procedure. A similar approach has been applied in Hearst & Lavoie (Reference Hearst and Lavoie2014).
$x = x_0$. As the parameters in (3.1) depend greatly upon the interval of sampling data considered, also the interval limits are determined inside the fitting procedure. A similar approach has been applied in Hearst & Lavoie (Reference Hearst and Lavoie2014).
In the present work, a developed region ![]() $I_d = [x_{min}, x_{max} ]$ is employed, where the right border of the interval is kept fixed to
$I_d = [x_{min}, x_{max} ]$ is employed, where the right border of the interval is kept fixed to ![]() $x_{max} = 30.0$, clear of possible – yet not evident – outflow condition effects, while
$x_{max} = 30.0$, clear of possible – yet not evident – outflow condition effects, while ![]() $x_{min}$ is discretely varied in the interval
$x_{min}$ is discretely varied in the interval ![]() $[0.015, 24.7]$ to seek an
$[0.015, 24.7]$ to seek an ![]() $x_{min}$ coordinate that ensures the best fit. The coordinate
$x_{min}$ coordinate that ensures the best fit. The coordinate ![]() $x_{min}$ will be taken as the start of the developed region. For each selection of a value for
$x_{min}$ will be taken as the start of the developed region. For each selection of a value for ![]() $x_{min}$, the virtual origin
$x_{min}$, the virtual origin ![]() $x_0$ is discretely varied within
$x_0$ is discretely varied within ![]() $I_0 = [0.015, x_{min}]$, as the singularity is not supposed to belong to
$I_0 = [0.015, x_{min}]$, as the singularity is not supposed to belong to ![]() $I_d$. The intervals of variation of both
$I_d$. The intervals of variation of both ![]() $x_{min}$ and
$x_{min}$ and ![]() $x_0$ are discretised by the same subdivision as the computational mesh. Parameters
$x_0$ are discretised by the same subdivision as the computational mesh. Parameters ![]() $A$ and
$A$ and ![]() $n$ are determined through a least-squares fit. Deviations between computed data and fitting laws are then calculated as the Euclidean norm of the error divided by the number of data points:
$n$ are determined through a least-squares fit. Deviations between computed data and fitting laws are then calculated as the Euclidean norm of the error divided by the number of data points:
 \begin{equation} e(x_0,x_{min}) = \frac{\left( \displaystyle{\sum\nolimits_{j=1}^{N_d}} \delta^2_j \right)^{1/2}}{N_d}. \end{equation}
\begin{equation} e(x_0,x_{min}) = \frac{\left( \displaystyle{\sum\nolimits_{j=1}^{N_d}} \delta^2_j \right)^{1/2}}{N_d}. \end{equation}
In (3.2), ![]() $\delta _j$ represents the difference between computed statistics and the least-squares fitted power-law approximation of
$\delta _j$ represents the difference between computed statistics and the least-squares fitted power-law approximation of ![]() $u_{rms}^2$ at the
$u_{rms}^2$ at the ![]() $j$th point of
$j$th point of ![]() $I_d$; and
$I_d$; and ![]() $N_d$ is the number of uniformly spaced points in the data fit region
$N_d$ is the number of uniformly spaced points in the data fit region ![]() $I_d$. The
$I_d$. The ![]() $(x_0,x_{min})$ couple which ensures the smallest deviation from computed data provides the final
$(x_0,x_{min})$ couple which ensures the smallest deviation from computed data provides the final ![]() $A$ and
$A$ and ![]() $n$ coefficients. This procedure leads to the results given in table 2 with error distribution as in figure 6. In the region of parameters investigated, only one minimum is found, which is located far from the boundaries of the region investigated. The dependence on porosity of the power-law exponents obtained is shown to be only weak in the Appendix.
$n$ coefficients. This procedure leads to the results given in table 2 with error distribution as in figure 6. In the region of parameters investigated, only one minimum is found, which is located far from the boundaries of the region investigated. The dependence on porosity of the power-law exponents obtained is shown to be only weak in the Appendix.
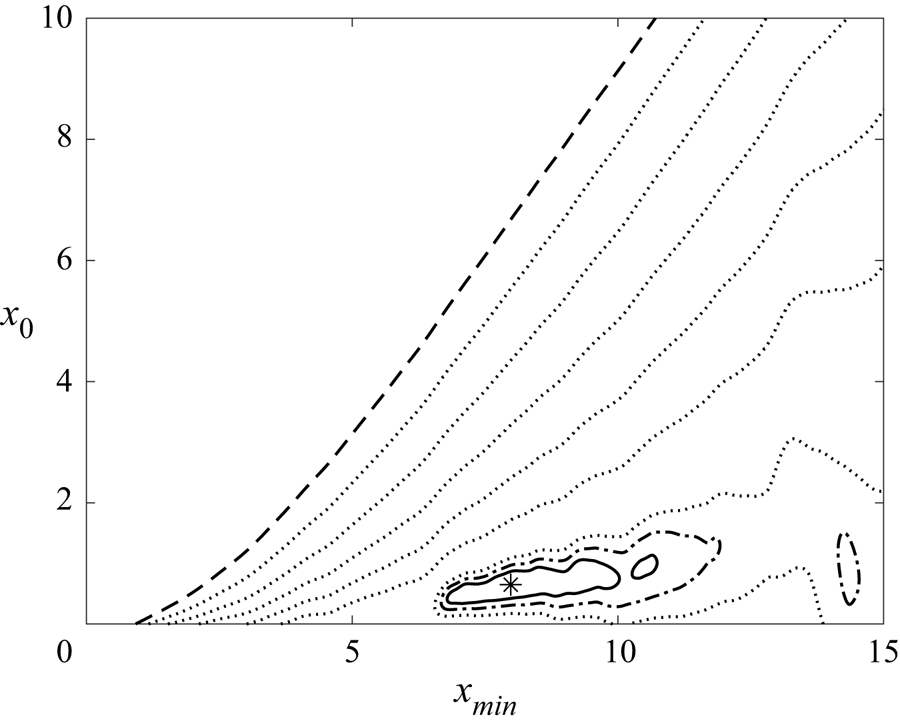
Figure 6. Contour lines of ![]() $\log _{10}(e)$, where
$\log _{10}(e)$, where ![]() $e$ is the normalised Euclidean norm of the error in (3.2): dashed line,
$e$ is the normalised Euclidean norm of the error in (3.2): dashed line, ![]() $\log _{10}(e) = -4.8$; dot-dashed line,
$\log _{10}(e) = -4.8$; dot-dashed line, ![]() $\log _{10}(e) = -6.03$; solid line,
$\log _{10}(e) = -6.03$; solid line, ![]() $\log _{10}(e) = -6.05$; and dotted line,
$\log _{10}(e) = -6.05$; and dotted line, ![]() $\log _{10}(e) \in [-6.00 -5.00]$, with lines separated by
$\log _{10}(e) \in [-6.00 -5.00]$, with lines separated by ![]() $\delta = 0.2$. A single minimum is found in the field, as indicated by the
$\delta = 0.2$. A single minimum is found in the field, as indicated by the ![]() $*$ symbol, which corresponds to
$*$ symbol, which corresponds to ![]() $x_0 = 0.648$ and
$x_0 = 0.648$ and ![]() $x_{min} = 7.98$. The singularity is not included in the domain, and thus
$x_{min} = 7.98$. The singularity is not included in the domain, and thus ![]() $x_{min} > x_0$.
$x_{min} > x_0$.
Table 2. Left boundary of the fitting interval ![]() $I_d$, virtual origin, multiplicative coefficient and decay exponent of the power laws in the form of equation (3.1) fitting
$I_d$, virtual origin, multiplicative coefficient and decay exponent of the power laws in the form of equation (3.1) fitting ![]() $u_{rms}^2$ and
$u_{rms}^2$ and ![]() $\langle k \rangle$.
$\langle k \rangle$.
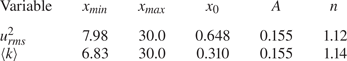
In order to check the dependence of the results from the fitting method employed, a procedure from the literature is also applied to the same set of data; this alternative technique is that utilised by Hearst & Lavoie (Reference Hearst and Lavoie2014). In the application of the method to the present case, the virtual origin ![]() $x_0$ and lower bound
$x_0$ and lower bound ![]() $x_{min}$ are varied within
$x_{min}$ are varied within ![]() $I_0 = [0, 4]$ and
$I_0 = [0, 4]$ and ![]() $[4, 14.7]$, respectively. For both
$[4, 14.7]$, respectively. For both ![]() $u_{rms}^2$ and
$u_{rms}^2$ and ![]() $\langle k \rangle$, the process converges after three iterations. Applied to
$\langle k \rangle$, the process converges after three iterations. Applied to ![]() $u_{rms}^2$, this fitting procedure provides
$u_{rms}^2$, this fitting procedure provides ![]() $x_0=0.610$ and
$x_0=0.610$ and ![]() $x_{min}=6.78$, which yield the estimate for
$x_{min}=6.78$, which yield the estimate for ![]() $\tilde {n}_u = 1.12$. In the case of
$\tilde {n}_u = 1.12$. In the case of ![]() $\langle k \rangle$, the values obtained are
$\langle k \rangle$, the values obtained are ![]() $x_0=0.360$,
$x_0=0.360$, ![]() $x_{min}=5.02$ and
$x_{min}=5.02$ and ![]() $\tilde {n}_k=1.14$. The results obtained by the method proposed by Hearst & Lavoie (Reference Hearst and Lavoie2014) are only marginally different from those obtained as described above and reported in table 2.
$\tilde {n}_k=1.14$. The results obtained by the method proposed by Hearst & Lavoie (Reference Hearst and Lavoie2014) are only marginally different from those obtained as described above and reported in table 2.
Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1966) found ![]() $1.15\leqslant n \leqslant 1.29$ for regular grids, while according to Mohamed & Larue (Reference Mohamed and Larue1990)
$1.15\leqslant n \leqslant 1.29$ for regular grids, while according to Mohamed & Larue (Reference Mohamed and Larue1990) ![]() $n \approx 1.3$. More recently, Krogstad & Davidson (Reference Krogstad and Davidson2010) found
$n \approx 1.3$. More recently, Krogstad & Davidson (Reference Krogstad and Davidson2010) found ![]() $n = 1.13 \pm 0.02$.
$n = 1.13 \pm 0.02$.
Besides the parameters ![]() $x_0$,
$x_0$, ![]() $A$ and
$A$ and ![]() $n$ in (3.1), the procedure provides the coordinate
$n$ in (3.1), the procedure provides the coordinate ![]() $x_{min}$ of the start of the developed region as the left boundary of the interval
$x_{min}$ of the start of the developed region as the left boundary of the interval ![]() $I_d$. All the subsequent fittings in this work will be carried out on
$I_d$. All the subsequent fittings in this work will be carried out on ![]() $I_d = [7.98, 30.0]$.
$I_d = [7.98, 30.0]$.
3.4. Turbulence decay rate
As opposed to experimental studies, where rate of dissipation ![]() $\langle \epsilon \rangle$ needs to be evaluated using the frozen turbulence assumption or isotropy (3.5), in DNS studies
$\langle \epsilon \rangle$ needs to be evaluated using the frozen turbulence assumption or isotropy (3.5), in DNS studies ![]() $\langle \epsilon \rangle$ can be computed directly from its definition,
$\langle \epsilon \rangle$ can be computed directly from its definition,
where ![]() $s_{ij} = ( \partial u_i/\partial x_{j} + \partial u_j/\partial x_{i} )/{2}$ is the fluctuating rate of strain. Figure 7 displays the spatial evolution of
$s_{ij} = ( \partial u_i/\partial x_{j} + \partial u_j/\partial x_{i} )/{2}$ is the fluctuating rate of strain. Figure 7 displays the spatial evolution of ![]() $\langle \epsilon \rangle$, together with the least-squares fitted power law in the form
$\langle \epsilon \rangle$, together with the least-squares fitted power law in the form ![]() $\langle \epsilon \rangle \sim a_{\epsilon } x^h$. The coefficients that fit the data over
$\langle \epsilon \rangle \sim a_{\epsilon } x^h$. The coefficients that fit the data over ![]() $I_d = [7.98, 30.0]$ are
$I_d = [7.98, 30.0]$ are ![]() $a_{\epsilon } = 0.217$ and
$a_{\epsilon } = 0.217$ and ![]() $h = -2.20$.
$h = -2.20$.
The scaling of dissipation ![]() $\langle \epsilon \rangle$ can also be set in relation to the scaling of
$\langle \epsilon \rangle$ can also be set in relation to the scaling of ![]() $\langle k \rangle$ in § 3.3. As also shown quantitatively in § 3.10, in the developed region of a statistically steady, high-Reynolds-number flow, one has
$\langle k \rangle$ in § 3.3. As also shown quantitatively in § 3.10, in the developed region of a statistically steady, high-Reynolds-number flow, one has
Equation (3.4) suggests that the decay exponent in this case should equal ![]() $h = - (n_k +1)$. In the present study,
$h = - (n_k +1)$. In the present study, ![]() $h = -2.20$ and
$h = -2.20$ and ![]() $n_k = 1.14$ are calculated. The percentage difference between
$n_k = 1.14$ are calculated. The percentage difference between ![]() $- (n_k + 1)$ and
$- (n_k + 1)$ and ![]() $h$ is below 3 %.
$h$ is below 3 %.
Dissipation is compared in figure 7 to the same quantity computed under the hypothesis of isotropic turbulence:
 \begin{equation} \langle\epsilon\rangle_{iso} = 15 \nu \left\langle \left( \frac{\partial u}{\partial x} \right)^2 \right\rangle. \end{equation}
\begin{equation} \langle\epsilon\rangle_{iso} = 15 \nu \left\langle \left( \frac{\partial u}{\partial x} \right)^2 \right\rangle. \end{equation}
The close similarity between ![]() $\langle \epsilon \rangle$ and
$\langle \epsilon \rangle$ and ![]() $\langle \epsilon \rangle _{iso}$ is only in apparent contradiction with isotropy ratios larger than 1.5 reported in § 3.2. From the demonstration by Taylor (Reference Taylor1935), it appears that hypotheses less strict than isotropy are required for equation (3.5) to hold. The weaker set of hypotheses hold true in the present case; see Corsini & Stalio (Reference Corsini and Stalio2020).
$\langle \epsilon \rangle _{iso}$ is only in apparent contradiction with isotropy ratios larger than 1.5 reported in § 3.2. From the demonstration by Taylor (Reference Taylor1935), it appears that hypotheses less strict than isotropy are required for equation (3.5) to hold. The weaker set of hypotheses hold true in the present case; see Corsini & Stalio (Reference Corsini and Stalio2020).
3.5. Length scales
The length scales examined for the characterisation of the turbulence generated by a metal foam are the Kolmogorov scale ![]() $\eta$, the Taylor microscale
$\eta$, the Taylor microscale ![]() $\lambda$ and the integral scales. All the length scales are computed directly from their definitions. Their distribution within the developed region is approximated by a power law of the distance
$\lambda$ and the integral scales. All the length scales are computed directly from their definitions. Their distribution within the developed region is approximated by a power law of the distance ![]() $x$. The range of variation of each length scale along
$x$. The range of variation of each length scale along ![]() $I_d$ is reported in table 1 together with data from the literature on classical grid turbulence.
$I_d$ is reported in table 1 together with data from the literature on classical grid turbulence.
3.5.1. Kolmogorov scale
The Kolmogorov scale is defined through dissipation ![]() $\langle \epsilon \rangle$. It is predicted from the power-law expression for
$\langle \epsilon \rangle$. It is predicted from the power-law expression for ![]() $\langle \epsilon \rangle$ (derived from the expression for
$\langle \epsilon \rangle$ (derived from the expression for ![]() $\langle k \rangle$) that
$\langle k \rangle$) that ![]() $\eta$ can be represented by a function of the form
$\eta$ can be represented by a function of the form ![]() $\eta \sim a_\eta x^s$, where
$\eta \sim a_\eta x^s$, where ![]() $s$ equals
$s$ equals ![]() $-h/4$ and finally
$-h/4$ and finally ![]() $s = (n_k + 1)/4$. The decay exponent for
$s = (n_k + 1)/4$. The decay exponent for ![]() $\langle k \rangle$ computed here,
$\langle k \rangle$ computed here, ![]() $n_k = 1.14$, gives
$n_k = 1.14$, gives ![]() $s = 0.54$. The power-law approximation is displayed in figure 8 together with the Kolmogorov scale, as computed from its definition: the fitting coefficients are
$s = 0.54$. The power-law approximation is displayed in figure 8 together with the Kolmogorov scale, as computed from its definition: the fitting coefficients are ![]() $a_\eta = 0.00291$ and
$a_\eta = 0.00291$ and ![]() $s = 0.55$. Very similar power-law parameters are obtained in this same flow configuration for a porosity
$s = 0.55$. Very similar power-law parameters are obtained in this same flow configuration for a porosity ![]() $\varepsilon = 0.97$; see the Appendix. Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971) provide Kolmogorov-scale measurements in their table 4, which grow like a power law of exponent
$\varepsilon = 0.97$; see the Appendix. Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971) provide Kolmogorov-scale measurements in their table 4, which grow like a power law of exponent ![]() $\hat {s} = 0.58$.
$\hat {s} = 0.58$.

Figure 8. Streamwise distribution of the Kolmogorov scale: dashed line, ![]() $\eta$ as calculated from its definition; and solid line,
$\eta$ as calculated from its definition; and solid line, ![]() $a_\eta x^s$, where
$a_\eta x^s$, where ![]() $a_\eta = 0.00291,\ s = 0.55$. The uniform grid spacing adopted in all directions is
$a_\eta = 0.00291,\ s = 0.55$. The uniform grid spacing adopted in all directions is ![]() $\Delta x_i = 0.0146$, which suggests that spatial resolution is high enough to represent the smallest scales of the turbulence.
$\Delta x_i = 0.0146$, which suggests that spatial resolution is high enough to represent the smallest scales of the turbulence.
3.5.2. Taylor microscale
Figure 9 displays the streamwise distribution of the Taylor microscale, defined by
 \begin{equation} u_{rms}^2 = \lambda^2 \left\langle\left( \frac{\partial u }{\partial x} \right)^2\right\rangle. \end{equation}
\begin{equation} u_{rms}^2 = \lambda^2 \left\langle\left( \frac{\partial u }{\partial x} \right)^2\right\rangle. \end{equation}
Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971) report Taylor-scale values in a few measurement points (see their table 4); their data fit a power law of exponent ![]() $c = 0.53$. It is predicted in the study by George (Reference George1992) that the Taylor scale of homogeneous isotropic turbulence increases in time with
$c = 0.53$. It is predicted in the study by George (Reference George1992) that the Taylor scale of homogeneous isotropic turbulence increases in time with ![]() $t^{1/2}$ and, for grid turbulence,
$t^{1/2}$ and, for grid turbulence, ![]() $\lambda$ grows as
$\lambda$ grows as ![]() $x^{1/2}$ in the laboratory frame. More recently, Kurian & Fransson (Reference Kurian and Fransson2009) reported that
$x^{1/2}$ in the laboratory frame. More recently, Kurian & Fransson (Reference Kurian and Fransson2009) reported that ![]() $\lambda$ increases approximately like the square-root of the streamwise coordinate. In the present study, fitting a power-law approximation of the form
$\lambda$ increases approximately like the square-root of the streamwise coordinate. In the present study, fitting a power-law approximation of the form ![]() $\lambda \sim a_\lambda x^c$ over
$\lambda \sim a_\lambda x^c$ over ![]() $I_d$ gives
$I_d$ gives ![]() $a_\lambda = 0.0577$ and
$a_\lambda = 0.0577$ and ![]() $c = 0.52$.
$c = 0.52$.

Figure 9. Streamwise distribution of the Taylor microscale: dashed line, ![]() $\lambda$ as calculated from its definition; and solid line,
$\lambda$ as calculated from its definition; and solid line, ![]() $a_\lambda x^c$, where
$a_\lambda x^c$, where ![]() $a_\lambda = 0.0577$ and
$a_\lambda = 0.0577$ and ![]() $c = 0.52$.
$c = 0.52$.
Figure 10 shows the behaviour of the turbulent Reynolds number. After a steep decrease in the vicinity of the metal foam, ![]() ${\textit {Re}}_{\lambda }$ reaches a plateau where
${\textit {Re}}_{\lambda }$ reaches a plateau where ![]() ${\textit {Re}}_{\lambda } \approx 80$. An expression relating the Taylor and the Kolmogorov scales can be obtained for isotropic turbulence through (3.5):
${\textit {Re}}_{\lambda } \approx 80$. An expression relating the Taylor and the Kolmogorov scales can be obtained for isotropic turbulence through (3.5):
Results from the present investigation, and not reported for brevity, show that the difference between ![]() $( \lambda / \eta )^2 / \sqrt {15}$ and
$( \lambda / \eta )^2 / \sqrt {15}$ and ![]() ${\textit {Re}}_{\lambda }$ is less than 3 % over the whole computational domain.
${\textit {Re}}_{\lambda }$ is less than 3 % over the whole computational domain.

Figure 10. Streamwise distribution of ![]() ${\textit {Re}}_{\lambda }$. The horizontal dashed line specifies the value
${\textit {Re}}_{\lambda }$. The horizontal dashed line specifies the value ![]() ${\textit {Re}}_{\lambda } = 80$.
${\textit {Re}}_{\lambda } = 80$.
3.5.3. Integral scales
The autocorrelation coefficient is defined as the ratio between the autocorrelation function of separation ![]() $\boldsymbol {r} = r \boldsymbol {e}_{j}$ and the autocorrelation function for
$\boldsymbol {r} = r \boldsymbol {e}_{j}$ and the autocorrelation function for ![]() $r = 0$:
$r = 0$:
The autocorrelation coefficients along ![]() $y$ of the streamwise
$y$ of the streamwise ![]() $\rho _{11}(x,r \boldsymbol {e}_{2})$ and the cross-flow
$\rho _{11}(x,r \boldsymbol {e}_{2})$ and the cross-flow ![]() $\rho _{22}(x,r \boldsymbol {e}_{2})$ velocity components are reported in figure 8 of Corsini & Stalio (Reference Corsini and Stalio2020). A distinction is made between the transverse and longitudinal correlations depending on the relative direction of velocity components and separation vector. Transverse correlations built with streamwise velocity fluctuations have longer tails with respect to longitudinal correlations built with spanwise fluctuations.
$\rho _{22}(x,r \boldsymbol {e}_{2})$ velocity components are reported in figure 8 of Corsini & Stalio (Reference Corsini and Stalio2020). A distinction is made between the transverse and longitudinal correlations depending on the relative direction of velocity components and separation vector. Transverse correlations built with streamwise velocity fluctuations have longer tails with respect to longitudinal correlations built with spanwise fluctuations.
Integral scales are defined as integrals over ![]() $r$ of autocorrelation coefficients:
$r$ of autocorrelation coefficients:
These depend upon the coordinates along non-homogeneous directions as well as on the direction of separation ![]() $\boldsymbol {e}_{j}$. In practice, since the computational domain has finite boundaries, the integral scales are calculated here as the distance over which the autocorrelation function decreases from
$\boldsymbol {e}_{j}$. In practice, since the computational domain has finite boundaries, the integral scales are calculated here as the distance over which the autocorrelation function decreases from ![]() $1$ to
$1$ to ![]() $1/\textrm {e}$, where
$1/\textrm {e}$, where ![]() $\textrm {e}$ is Euler's number. For the calculation of integral scales, correlations are assumed to decay exponentially.
$\textrm {e}$ is Euler's number. For the calculation of integral scales, correlations are assumed to decay exponentially.
Integral scales for the present case are based on the streamwise or the cross-flow velocity components. Given the inhomogeneity of the streamwise direction, separation is set in the cross-flow directions ![]() $\boldsymbol {e}_{2}$ and
$\boldsymbol {e}_{2}$ and ![]() $\boldsymbol {e}_{3}$. Thus, the integral scale based on the streamwise velocity is always transverse and will be denoted by
$\boldsymbol {e}_{3}$. Thus, the integral scale based on the streamwise velocity is always transverse and will be denoted by ![]() $L$. The integral scales based on cross-flow velocity components can be either longitudinal or transverse and are denoted by
$L$. The integral scales based on cross-flow velocity components can be either longitudinal or transverse and are denoted by ![]() $L_g$ and
$L_g$ and ![]() $L_t$, respectively. As statistically
$L_t$, respectively. As statistically ![]() $L_{11} (x,\boldsymbol {e}_{2}) = L_{11} (x,\boldsymbol {e}_{3}) = L (x)$,
$L_{11} (x,\boldsymbol {e}_{2}) = L_{11} (x,\boldsymbol {e}_{3}) = L (x)$, ![]() $L_{22} (x,\boldsymbol {e}_{2}) = L_{33} (x,\boldsymbol {e}_{3}) = L_g (x)$ and
$L_{22} (x,\boldsymbol {e}_{2}) = L_{33} (x,\boldsymbol {e}_{3}) = L_g (x)$ and ![]() $L_{33} (x,\boldsymbol {e}_{2}) = L_{22} (x,\boldsymbol {e}_{3}) = L_t (x)$, these equalities have been exploited in the calculation of integral scales.
$L_{33} (x,\boldsymbol {e}_{2}) = L_{22} (x,\boldsymbol {e}_{3}) = L_t (x)$, these equalities have been exploited in the calculation of integral scales.
Figure 11 displays the integral scales. The power-law approximations ![]() $L \sim a_L x^q$ have the coefficients reported in table 3; the exponents computed are very close to the
$L \sim a_L x^q$ have the coefficients reported in table 3; the exponents computed are very close to the ![]() $L \sim x^{1/2}$ behaviour predicted by Wang & George (Reference Wang and George2002). Also, in the case of higher porosity presented in the Appendix, the power-law exponent is close to
$L \sim x^{1/2}$ behaviour predicted by Wang & George (Reference Wang and George2002). Also, in the case of higher porosity presented in the Appendix, the power-law exponent is close to ![]() $1/2$.
$1/2$.

Figure 11. Streamwise distribution of the integral scales: dot-dashed line, streamwise integral scale ![]() $L$; dashed line, longitudinal integral scale
$L$; dashed line, longitudinal integral scale ![]() $L_g$; dotted line, transverse integral scale
$L_g$; dotted line, transverse integral scale ![]() $L_t$; and solid line, power-law approximations of the different scales.
$L_t$; and solid line, power-law approximations of the different scales.
Table 3. Parameters of the power-law functions of the form ![]() $f(x) \sim a x^b$ fitting the turbulent quantities analysed.
$f(x) \sim a x^b$ fitting the turbulent quantities analysed.

Notice that ![]() $L$ is one order of magnitude smaller than the domain size, the transverse length of which is
$L$ is one order of magnitude smaller than the domain size, the transverse length of which is ![]() $11.25 d_p$; this suggests that the imposed lateral periodic boundary conditions can satisfactorily represent cross-flow homogeneity in the present case. The evolution of the Reynolds number based on the integral scale, defined as
$11.25 d_p$; this suggests that the imposed lateral periodic boundary conditions can satisfactorily represent cross-flow homogeneity in the present case. The evolution of the Reynolds number based on the integral scale, defined as ![]() ${\textit {Re}}_{L} \equiv L u_{rms} /\nu$, along the
${\textit {Re}}_{L} \equiv L u_{rms} /\nu$, along the ![]() $x$-axis is displayed in figure 9 of Corsini & Stalio (Reference Corsini and Stalio2020).
$x$-axis is displayed in figure 9 of Corsini & Stalio (Reference Corsini and Stalio2020).
3.6. Dissipation rate coefficient
In high-Reynolds-number turbulent flows away from solid walls, the dissipation rate can be scaled on the integral length scale and velocity fluctuations through an order-one constant:
Figure 12 shows that, in the present case, after an initial steep increase for ![]() $x < 2$, the dissipation rate coefficient
$x < 2$, the dissipation rate coefficient ![]() $C_{\epsilon }$ based on
$C_{\epsilon }$ based on ![]() $L$ fluctuates over
$L$ fluctuates over ![]() $I_d$ between
$I_d$ between ![]() $0.45$ and
$0.45$ and ![]() $0.50$, where its spatial average is
$0.50$, where its spatial average is ![]() $\bar {C}_{\epsilon } = 0.483$. This value is very close to values reported in Pearson, Krogstad & van de Water (Reference Pearson, Krogstad and van de Water2002) for shear turbulence at different
$\bar {C}_{\epsilon } = 0.483$. This value is very close to values reported in Pearson, Krogstad & van de Water (Reference Pearson, Krogstad and van de Water2002) for shear turbulence at different ![]() ${\textit {Re}}_\lambda$ numbers.
${\textit {Re}}_\lambda$ numbers.

Figure 12. Streamwise distribution of ![]() $C_{\epsilon } = {\langle \epsilon \rangle L}/{u_{rms}^{3}}$: solid line, based on the streamwise integral scale
$C_{\epsilon } = {\langle \epsilon \rangle L}/{u_{rms}^{3}}$: solid line, based on the streamwise integral scale ![]() $L$; dashed line, based on the longitudinal integral scale
$L$; dashed line, based on the longitudinal integral scale ![]() $L_g$; and dotted line, based on the transverse integral scale
$L_g$; and dotted line, based on the transverse integral scale ![]() $L_t$.
$L_t$.
With regard to the initial steep increase, in recent years Vassilicos and coworkers have observed that, close to the turbulence-generating grid, there is a region characterised by spectra that closely match the ![]() ${-5/3}$ power law, in conjunction with an increase in
${-5/3}$ power law, in conjunction with an increase in ![]() $C_\epsilon$. In the hypothesis of
$C_\epsilon$. In the hypothesis of ![]() $\langle \epsilon \rangle = \langle \epsilon \rangle _{iso}$, combining the definition (3.10) with equation (3.5) leads to
$\langle \epsilon \rangle = \langle \epsilon \rangle _{iso}$, combining the definition (3.10) with equation (3.5) leads to
As only small variations of the ratio between length scales ![]() $L/\lambda$ are observed for given Reynolds number of the mesh size,
$L/\lambda$ are observed for given Reynolds number of the mesh size, ![]() $C_{\epsilon }$ is seen to increase like
$C_{\epsilon }$ is seen to increase like ![]() ${\textit {Re}}_{\lambda }^{-1}$. This behaviour is reported for both fractal and regular grids (Valente & Vassilicos Reference Valente and Vassilicos2012).
${\textit {Re}}_{\lambda }^{-1}$. This behaviour is reported for both fractal and regular grids (Valente & Vassilicos Reference Valente and Vassilicos2012).
Equation (3.11) is studied for the present case in figure 13, where the logarithmic plot emphasises the ![]() $C_{\epsilon } (Re_{\lambda })$ behaviour close to the metal foam. Corresponding to the initial steep decrease in
$C_{\epsilon } (Re_{\lambda })$ behaviour close to the metal foam. Corresponding to the initial steep decrease in ![]() ${\textit {Re}}_{\lambda }$ shown in figure 10,
${\textit {Re}}_{\lambda }$ shown in figure 10, ![]() $C_\epsilon$ is seen to increase like
$C_\epsilon$ is seen to increase like ![]() $Re_{\lambda }^{-1}$. In the same region, a well-defined
$Re_{\lambda }^{-1}$. In the same region, a well-defined ![]() $-5/3$ energy spectra behaviour is observed over a broader wavenumber range than the fully developed region; see the inset of figure 15 in § 3.8. The situation described in Valente & Vassilicos (Reference Valente and Vassilicos2012) is thus observed in the present case.
$-5/3$ energy spectra behaviour is observed over a broader wavenumber range than the fully developed region; see the inset of figure 15 in § 3.8. The situation described in Valente & Vassilicos (Reference Valente and Vassilicos2012) is thus observed in the present case.

Figure 13. Plot of ![]() $C_{\epsilon }$ as a function of
$C_{\epsilon }$ as a function of ![]() $Re_{\lambda }$. The dashed line follows
$Re_{\lambda }$. The dashed line follows ![]() $Re_{\lambda }^{-1}$.
$Re_{\lambda }^{-1}$.
The streamwise evolution of ![]() $C_\epsilon$ experiences a transition between the
$C_\epsilon$ experiences a transition between the ![]() $Re_{\lambda }^{-1}$ behaviour and a region where the variations in
$Re_{\lambda }^{-1}$ behaviour and a region where the variations in ![]() $C_\epsilon$ are much smaller; see figures 12 and 13. This transition is about
$C_\epsilon$ are much smaller; see figures 12 and 13. This transition is about ![]() $x = 2$. The turbulent kinetic energy budgets reported in § 3.10 indicate that, downstream of this location, the turbulent transport terms become negligible and the mean advection of
$x = 2$. The turbulent kinetic energy budgets reported in § 3.10 indicate that, downstream of this location, the turbulent transport terms become negligible and the mean advection of ![]() $\langle k \rangle$ equals dissipation. On the contrary, for
$\langle k \rangle$ equals dissipation. On the contrary, for ![]() $x<2$, this equality does not hold, and the variations of
$x<2$, this equality does not hold, and the variations of ![]() $C_\epsilon$ suggest a non-equilibrium condition between energy at the large scales and dissipation. It should be noted that the present results confirm the predictions reported by Tennekes & Lumley (Reference Tennekes and Lumley1972) in their (3.2.29) and (3.2.30), where transition is expected at streamwise distances from the grid that are much larger than the integral scale. In the present configuration,
$C_\epsilon$ suggest a non-equilibrium condition between energy at the large scales and dissipation. It should be noted that the present results confirm the predictions reported by Tennekes & Lumley (Reference Tennekes and Lumley1972) in their (3.2.29) and (3.2.30), where transition is expected at streamwise distances from the grid that are much larger than the integral scale. In the present configuration, ![]() $x = 2$ corresponds to
$x = 2$ corresponds to ![]() $x \approx 6 L$.
$x \approx 6 L$.
In the theory by Richardson and Kolmogorov, the constancy of ![]() $C_\epsilon$ requires that turbulence is at a high Reynolds number and far from solid walls. While the small variations of
$C_\epsilon$ requires that turbulence is at a high Reynolds number and far from solid walls. While the small variations of ![]() $C_\epsilon$ in the fully developed region can be attributed to the Reynolds number, which is not very high, the steep increase in
$C_\epsilon$ in the fully developed region can be attributed to the Reynolds number, which is not very high, the steep increase in ![]() $C_\epsilon$ in the vicinity of the porous matrix (
$C_\epsilon$ in the vicinity of the porous matrix (![]() $x < 2$) is to be ascribed to the vicinity of the solid filaments and ultimately to non-negligible turbulent transport terms in the budget equation of
$x < 2$) is to be ascribed to the vicinity of the solid filaments and ultimately to non-negligible turbulent transport terms in the budget equation of ![]() $\langle k \rangle$.
$\langle k \rangle$.
3.7. Is grid turbulence Saffman turbulence?
In recent articles (Krogstad & Davidson Reference Krogstad and Davidson2010; Kitamura et al. Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014) it was discussed whether grid turbulence can be considered to be of the Saffman type. Both Krogstad & Davidson (Reference Krogstad and Davidson2010) and Kitamura et al. (Reference Kitamura, Nagata, Sakai, Sasoh, Terashima, Saito and Harasaki2014) conclude that grid turbulence is Saffman turbulence.
The theory by Saffman (Reference Saffman1967) describes the decay of homogeneous turbulence as
where ![]() $K$ and
$K$ and ![]() $K^\prime$ are constants and
$K^\prime$ are constants and ![]() $C$ is expressed by an invariant integral. Both equations (3.12a,b) have to hold for turbulence to be of the Saffman type. This is sometimes expressed by the requirement that
$C$ is expressed by an invariant integral. Both equations (3.12a,b) have to hold for turbulence to be of the Saffman type. This is sometimes expressed by the requirement that ![]() $u_{rms}^2 L^3 = \text {const.}$ during decay, but the latter is a necessary, not sufficient, condition for Saffman turbulence.
$u_{rms}^2 L^3 = \text {const.}$ during decay, but the latter is a necessary, not sufficient, condition for Saffman turbulence.
The exponents reported in tables 2 and 3 suggest that turbulence investigated in the present study is not of the Saffman type. Figure 14 provides graphical confirmation for this conclusion.

Figure 14. Streamwise evolution of the product of powers of the integral scale times powers of velocity fluctuations: solid line, ![]() $u_{rms}^2 L^2$; dashed line,
$u_{rms}^2 L^2$; dashed line, ![]() $u_{rms}^2 L^3$; and dot-dashed line,
$u_{rms}^2 L^3$; and dot-dashed line, ![]() $u_{rms}^2 L^5$. Saffman turbulence requires the constancy of
$u_{rms}^2 L^5$. Saffman turbulence requires the constancy of ![]() $u_{rms}^2 L^3 = \text {const.}$, not observed here.
$u_{rms}^2 L^3 = \text {const.}$, not observed here.
In the fully developed region of grid turbulence, as well as in the case investigated here, the advection of turbulent kinetic energy is almost perfectly balanced by dissipation:
(see § 3.4). Setting ![]() $n_k = n_u = n$, (3.13) combined with the definition of
$n_k = n_u = n$, (3.13) combined with the definition of ![]() $C_\epsilon$ in (3.10) and the hypotheses
$C_\epsilon$ in (3.10) and the hypotheses ![]() $L \sim x^q$ and
$L \sim x^q$ and ![]() $C_\epsilon \sim x^{\,f}$ leads to the following relation:
$C_\epsilon \sim x^{\,f}$ leads to the following relation:
As is apparent from (3.12a,b) and (3.14), grid turbulence generated at ![]() $n = 6/5$ is not of the Saffman type unless
$n = 6/5$ is not of the Saffman type unless ![]() $C_\epsilon$ stays constant during kinetic energy decay (
$C_\epsilon$ stays constant during kinetic energy decay (![]() $f = 0$).
$f = 0$).
3.8. Spectral scaling and energy transfer
One-dimensional spectra ![]() $E_{ii}(\kappa _j)$ are obtained from the discrete Fourier transform of the two-point velocity correlation functions along
$E_{ii}(\kappa _j)$ are obtained from the discrete Fourier transform of the two-point velocity correlation functions along ![]() $\boldsymbol {e}_{j}$, where
$\boldsymbol {e}_{j}$, where ![]() $\kappa _j$ is the
$\kappa _j$ is the ![]() $j$th component of the wavenumber vector. Only
$j$th component of the wavenumber vector. Only ![]() $j = 2$ and
$j = 2$ and ![]() $j = 3$ are used here because the streamwise direction is not homogeneous. Depending upon the pairing between velocity and wavenumber components, three distinct spectra can be calculated: streamwise spectrum
$j = 3$ are used here because the streamwise direction is not homogeneous. Depending upon the pairing between velocity and wavenumber components, three distinct spectra can be calculated: streamwise spectrum ![]() $E_s = E_{11}(\kappa _j)$, longitudinal spectrum
$E_s = E_{11}(\kappa _j)$, longitudinal spectrum ![]() $E_g = E_{jj}(\kappa _j)$ and transverse spectrum
$E_g = E_{jj}(\kappa _j)$ and transverse spectrum ![]() $E_t = E_{ii}(\kappa _j)$, where
$E_t = E_{ii}(\kappa _j)$, where ![]() $i = 2$,
$i = 2$, ![]() $j = 3$ or
$j = 3$ or ![]() $i = 3$,
$i = 3$, ![]() $j = 2$.
$j = 2$.
While, in general, spectra at different stages of the decay could be expected to scale with different reference quantities, it is observed here that, as factors ![]() $\eta u_{\eta }^2$,
$\eta u_{\eta }^2$, ![]() $\lambda u_{rms}^2$ and
$\lambda u_{rms}^2$ and ![]() $L u_{rms}^2$ evolve at very similar rates in the streamwise direction (see table 3), any of those can be used equivalently. Spectra scaled by
$L u_{rms}^2$ evolve at very similar rates in the streamwise direction (see table 3), any of those can be used equivalently. Spectra scaled by ![]() $\lambda u_{rms}^2$ and evaluated at increasing distance along the
$\lambda u_{rms}^2$ and evaluated at increasing distance along the ![]() $x$-axis are displayed in figure 15.
$x$-axis are displayed in figure 15.

Figure 15. Streamwise one-dimensional spectra normalised in Taylor variables at increasing distance from the metal foam, ![]() $x = 10$,
$x = 10$, ![]() $15$,
$15$, ![]() $20$,
$20$, ![]() $25$ and
$25$ and ![]() $30$. The inset displays the power-law scaling exhibited by the spectrum at
$30$. The inset displays the power-law scaling exhibited by the spectrum at ![]() $x = 2$, as indicated by the dashed line with slope
$x = 2$, as indicated by the dashed line with slope ![]() $-5/3$.
$-5/3$.
Figure 16 compares the three types of spectra (![]() $E_s$,
$E_s$, ![]() $E_g$ and
$E_g$ and ![]() $E_t$) at a coordinate
$E_t$) at a coordinate ![]() $x = 20$. For
$x = 20$. For ![]() $\kappa _2 \eta > 0.2$, the streamwise and transverse spectra almost coincide, which is confirmation that anisotropy is at large scales only; see Mohamed & Larue (Reference Mohamed and Larue1990) and Corsini & Stalio (Reference Corsini and Stalio2020). Only a narrow range in the wavenumber space (
$\kappa _2 \eta > 0.2$, the streamwise and transverse spectra almost coincide, which is confirmation that anisotropy is at large scales only; see Mohamed & Larue (Reference Mohamed and Larue1990) and Corsini & Stalio (Reference Corsini and Stalio2020). Only a narrow range in the wavenumber space (![]() $0.025 < \kappa _2 \eta < 0.1$) is noticed where
$0.025 < \kappa _2 \eta < 0.1$) is noticed where ![]() $E_s$ exhibits a
$E_s$ exhibits a ![]() $- 5/3$ behaviour. Figure 16 includes the longitudinal spectra
$- 5/3$ behaviour. Figure 16 includes the longitudinal spectra ![]() $E_{11}(\kappa _1)$ of Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971) for two regular grids of different mesh size and
$E_{11}(\kappa _1)$ of Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971) for two regular grids of different mesh size and ![]() ${\textit {Re}}_{\lambda }$ values in the same range as the present case (
${\textit {Re}}_{\lambda }$ values in the same range as the present case (![]() ${\textit {Re}}_{\lambda } = 65$ and
${\textit {Re}}_{\lambda } = 65$ and ![]() $41$, compared to the present
$41$, compared to the present ![]() ${\textit {Re}}_{\lambda } = 81$). Close agreement is observed between measurements in turbulence generated by classical grids and turbulence simulated in the high-porosity metal foam for
${\textit {Re}}_{\lambda } = 81$). Close agreement is observed between measurements in turbulence generated by classical grids and turbulence simulated in the high-porosity metal foam for ![]() $\kappa _2 \eta > 0.1$.
$\kappa _2 \eta > 0.1$.

Figure 16. Comparison of streamwise, longitudinal and transverse spectra with Kolmogorov scaling at ![]() $x = 20$ (
$x = 20$ (![]() ${\textit {Re}}_{\lambda } = 81$): solid line,
${\textit {Re}}_{\lambda } = 81$): solid line, ![]() $E_s$; dot-dashed line,
$E_s$; dot-dashed line, ![]() $E_g$; dotted line,
$E_g$; dotted line, ![]() $E_t$; and dashed line,
$E_t$; and dashed line, ![]() $(\kappa _2\eta )^{-5/3}$. Symbols are longitudinal spectra of grid turbulence experiments from Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971):
$(\kappa _2\eta )^{-5/3}$. Symbols are longitudinal spectra of grid turbulence experiments from Comte-Bellot & Corrsin (Reference Comte-Bellot and Corrsin1971): ![]() $\times$,
$\times$, ![]() $M^* = 50.8$ mm (
$M^* = 50.8$ mm (![]() $x^*/M^* = 98$,
$x^*/M^* = 98$, ![]() ${\textit {Re}}_{\lambda } = 65$); and
${\textit {Re}}_{\lambda } = 65$); and ![]() $+$,
$+$, ![]() $M^* = 25.4$ mm (
$M^* = 25.4$ mm (![]() $x^*/M^* = 120$,
$x^*/M^* = 120$, ![]() ${\textit {Re}}_{\lambda } = 41$). Asterisk
${\textit {Re}}_{\lambda } = 41$). Asterisk ![]() $^*$ denotes quantities expressed in dimensional form.
$^*$ denotes quantities expressed in dimensional form.
The present results match canonical grid turbulence spectra for ![]() $\kappa _2 \eta > 0.1$, the
$\kappa _2 \eta > 0.1$, the ![]() $-5/3$ law is not observed for wavenumbers
$-5/3$ law is not observed for wavenumbers ![]() $\kappa _2 \eta > 0.1$, and local isotropy is observed for
$\kappa _2 \eta > 0.1$, and local isotropy is observed for ![]() $\kappa _2 \eta > 0.2$. That is the range of scales where dissipation becomes non-negligible. The distinction between scales containing the bulk of the energy from those responsible for dissipation is done by considering the energy spectrum
$\kappa _2 \eta > 0.2$. That is the range of scales where dissipation becomes non-negligible. The distinction between scales containing the bulk of the energy from those responsible for dissipation is done by considering the energy spectrum ![]() $E(\kappa )$ and the dissipative spectrum
$E(\kappa )$ and the dissipative spectrum ![]() $D(\kappa ) = 2 \nu \kappa ^2 E(\kappa )$.
$D(\kappa ) = 2 \nu \kappa ^2 E(\kappa )$.
The turbulence spectrum ![]() $E(\kappa )$ is obtained by
$E(\kappa )$ is obtained by
where the summation convention is applied. The spectrum in (3.15) removes the directional information from both the velocities and the Fourier modes, as ![]() $E(\kappa )$ is given as a function of the wavenumber magnitude
$E(\kappa )$ is given as a function of the wavenumber magnitude ![]() $\kappa = |\boldsymbol {\kappa }|$.
$\kappa = |\boldsymbol {\kappa }|$.
The kinetic energy cumulated at wavenumbers lower than ![]() $\kappa$ is
$\kappa$ is
the complement to ![]() $k_{(0,\kappa )}$ is indicated by
$k_{(0,\kappa )}$ is indicated by ![]() $k_{(\kappa ,\infty )}$. The corresponding quantities for the dissipation are obtained in the same fashion using
$k_{(\kappa ,\infty )}$. The corresponding quantities for the dissipation are obtained in the same fashion using ![]() $D(\kappa )$ and are indicated by
$D(\kappa )$ and are indicated by ![]() $\langle \epsilon \rangle _{(0,\kappa )}$ and
$\langle \epsilon \rangle _{(0,\kappa )}$ and ![]() $\langle \epsilon \rangle _{(\kappa ,\infty )}$. In figure 17 the fraction of cumulative turbulent kinetic energy at wavenumbers higher than
$\langle \epsilon \rangle _{(\kappa ,\infty )}$. In figure 17 the fraction of cumulative turbulent kinetic energy at wavenumbers higher than ![]() $\kappa$ and the fraction of cumulative dissipation at wavenumbers lower than
$\kappa$ and the fraction of cumulative dissipation at wavenumbers lower than ![]() $\kappa$ at a distance from the foam
$\kappa$ at a distance from the foam ![]() $x=20$ are depicted as functions of
$x=20$ are depicted as functions of ![]() $\kappa \eta$ and of the corresponding wavelength
$\kappa \eta$ and of the corresponding wavelength ![]() $\ell /\eta = 2 {\rm \pi}/ \kappa \eta$. The peak of the energy spectrum occurs at
$\ell /\eta = 2 {\rm \pi}/ \kappa \eta$. The peak of the energy spectrum occurs at ![]() $\kappa \eta \approx 0.02$ (see figure 16) but it may be observed that the main fraction of the kinetic energy (
$\kappa \eta \approx 0.02$ (see figure 16) but it may be observed that the main fraction of the kinetic energy (![]() $k_{(\kappa ,\infty )} = 0.1 k$) is contained in the range of wavenumbers up to
$k_{(\kappa ,\infty )} = 0.1 k$) is contained in the range of wavenumbers up to ![]() $\kappa \eta \approx 0.25$, one decade further. The peak of dissipation is roughly at
$\kappa \eta \approx 0.25$, one decade further. The peak of dissipation is roughly at ![]() $\kappa \eta \approx 0.25$ (which corresponds to the maximum derivative in
$\kappa \eta \approx 0.25$ (which corresponds to the maximum derivative in ![]() $\langle \epsilon \rangle _{(0,\kappa )}/\langle \epsilon \rangle$). The contribution to dissipation reaches
$\langle \epsilon \rangle _{(0,\kappa )}/\langle \epsilon \rangle$). The contribution to dissipation reaches ![]() $\langle \epsilon \rangle _{(0,\kappa )}= 0.9\langle \epsilon \rangle$ at
$\langle \epsilon \rangle _{(0,\kappa )}= 0.9\langle \epsilon \rangle$ at ![]() $\kappa \eta \approx 0.7$. The bulk of turbulent kinetic energy is contained in motions of length scales
$\kappa \eta \approx 0.7$. The bulk of turbulent kinetic energy is contained in motions of length scales ![]() $\ell > 25 \eta \approx \frac {1}{2} L$; this range could be viewed as the energy-containing range. On the other hand, the dissipation is effective at the length scales
$\ell > 25 \eta \approx \frac {1}{2} L$; this range could be viewed as the energy-containing range. On the other hand, the dissipation is effective at the length scales ![]() $10 \eta < \ell < 50 \eta$. The overlap between
$10 \eta < \ell < 50 \eta$. The overlap between ![]() $k_{(\kappa ,\infty )}$ and
$k_{(\kappa ,\infty )}$ and ![]() $\langle \epsilon \rangle _{(0,\kappa )}$ reveals that energy starts to be dissipated at a length scale where the energy content is non-negligible.
$\langle \epsilon \rangle _{(0,\kappa )}$ reveals that energy starts to be dissipated at a length scale where the energy content is non-negligible.

Figure 17. Normalised complement of the cumulative kinetic energy and normalised cumulative dissipation against wavenumber ![]() $\kappa \eta$ and wavelength
$\kappa \eta$ and wavelength ![]() $\ell /\eta$ at
$\ell /\eta$ at ![]() $x = 20$: solid line,
$x = 20$: solid line, ![]() $k_{(\kappa ,\infty )}/k$; and dashed line,
$k_{(\kappa ,\infty )}/k$; and dashed line, ![]() $\langle \epsilon \rangle _{(0,\kappa )}/\langle \epsilon \rangle$.
$\langle \epsilon \rangle _{(0,\kappa )}/\langle \epsilon \rangle$.
3.9. Structure functions
In this section, the local structure of turbulence is investigated at ![]() $x = 25$ by analysing the scaling properties of the structure functions with separation
$x = 25$ by analysing the scaling properties of the structure functions with separation ![]() $r$. The general definition is given by
$r$. The general definition is given by
Because of turbulence decay along ![]() $x$, two different structure functions are identified in this work: longitudinal structure functions
$x$, two different structure functions are identified in this work: longitudinal structure functions ![]() $\langle (\delta u_{g})^{p}\rangle = \langle (\delta u_{j,j})^{p}\rangle$ and transverse structure functions
$\langle (\delta u_{g})^{p}\rangle = \langle (\delta u_{j,j})^{p}\rangle$ and transverse structure functions ![]() $\langle (\delta u_{t})^{p}\rangle = \langle (\delta u_{i,j})^{p}\rangle$, where
$\langle (\delta u_{t})^{p}\rangle = \langle (\delta u_{i,j})^{p}\rangle$, where ![]() $i=2$,
$i=2$, ![]() $j=3$ or
$j=3$ or ![]() $i=3$,
$i=3$, ![]() $j=2$.
$j=2$.
According to the first, original theory by Kolmogorov (Reference Kolmogorov1941), for high Reynolds numbers when the separation lies in the inertial subrange ![]() $\eta \ll r \ll L$, the moments of velocity difference
$\eta \ll r \ll L$, the moments of velocity difference ![]() $\langle (\delta u_{g})^{p}\rangle$ take a universal form that depends only on
$\langle (\delta u_{g})^{p}\rangle$ take a universal form that depends only on ![]() $\langle \epsilon \rangle$ through the following scaling property:
$\langle \epsilon \rangle$ through the following scaling property:
In the refined similarity theory (Kolmogorov Reference Kolmogorov1962), the intermittency effects are taken into account by rewriting expression (3.18) in terms of ![]() $\epsilon _{r}$, the dissipation averaged over a volume of linear dimension
$\epsilon _{r}$, the dissipation averaged over a volume of linear dimension ![]() $r$, and assuming that
$r$, and assuming that ![]() $\epsilon _{r}$ has a log-normal distribution,
$\epsilon _{r}$ has a log-normal distribution,
where ![]() $\mu$ is the exponent of the dissipation autocorrelation function,
$\mu$ is the exponent of the dissipation autocorrelation function,
again for inertial range separations (Monin & Yaglom Reference Monin and Yaglom1975).
Given the Reynolds number ![]() ${\textit {Re}}_{\lambda } \approx 80$ of the present case, the study is conducted using the extended self-similarity (ESS) observation by Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). The
${\textit {Re}}_{\lambda } \approx 80$ of the present case, the study is conducted using the extended self-similarity (ESS) observation by Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). The ![]() $p$th moments of velocity differences
$p$th moments of velocity differences ![]() $\langle (\delta u_{g})^{p}\rangle$ calculated at moderate Reynolds number are characterised by the same scaling exponents as in the high-Reynolds-number case when
$\langle (\delta u_{g})^{p}\rangle$ calculated at moderate Reynolds number are characterised by the same scaling exponents as in the high-Reynolds-number case when ![]() $\langle (\delta u_{g})^{p}\rangle$ are treated as functions of
$\langle (\delta u_{g})^{p}\rangle$ are treated as functions of ![]() $\langle |\delta u_{g}|^{3}\rangle$. The resulting exponents are indicated by
$\langle |\delta u_{g}|^{3}\rangle$. The resulting exponents are indicated by ![]() $\xi _{g}^{p} = \zeta _{g}^{p}/\zeta _{g}^{3}$ to discriminate them from those evaluated directly,
$\xi _{g}^{p} = \zeta _{g}^{p}/\zeta _{g}^{3}$ to discriminate them from those evaluated directly, ![]() $\zeta _{g}^{p}$. The quality of the ESS scaling is displayed in figure 18 and in table 4. Errors are calculated by summing the uncertainty obtained from the estimate of scaling in the two spatial directions
$\zeta _{g}^{p}$. The quality of the ESS scaling is displayed in figure 18 and in table 4. Errors are calculated by summing the uncertainty obtained from the estimate of scaling in the two spatial directions ![]() $y$ and
$y$ and ![]() $z$ and by modifying the scaling range over which
$z$ and by modifying the scaling range over which ![]() $\xi _{g}^{p}$ is evaluated in the interval
$\xi _{g}^{p}$ is evaluated in the interval ![]() $[3,30]\eta$. Data from the literature reported for comparison in table 4 are at
$[3,30]\eta$. Data from the literature reported for comparison in table 4 are at ![]() ${\textit {Re}}_{\lambda }$ comparable to the present, i.e. of order
${\textit {Re}}_{\lambda }$ comparable to the present, i.e. of order ![]() ${\sim }10^2$, except for those by Iyer, Sreenivasan & Yeung (Reference Iyer, Sreenivasan and Yeung2017), which are obtained at
${\sim }10^2$, except for those by Iyer, Sreenivasan & Yeung (Reference Iyer, Sreenivasan and Yeung2017), which are obtained at ![]() ${\textit {Re}}_{\lambda } \approx 1300$ and a high degree of isotropy.
${\textit {Re}}_{\lambda } \approx 1300$ and a high degree of isotropy.

Figure 18. Log–log plot of second-, sixth- and tenth-order longitudinal structure functions versus ![]() $\langle |\delta u_{g}|^{3}\rangle$ at the position
$\langle |\delta u_{g}|^{3}\rangle$ at the position ![]() $x=25$:
$x=25$: ![]() ${\Delta}$,
${\Delta}$, ![]() $p=2$;
$p=2$; ![]() $\square$,
$\square$, ![]() $p=6$; and
$p=6$; and ![]() $\diamond$,
$\diamond$, ![]() $p=10$. The straight lines superimposed onto the curves are the power laws resulting from the fitting procedure in the extended inertial range indicated by the dashed vertical lines. This range starts at
$p=10$. The straight lines superimposed onto the curves are the power laws resulting from the fitting procedure in the extended inertial range indicated by the dashed vertical lines. This range starts at ![]() $3\eta$ and ends at
$3\eta$ and ends at ![]() $30\eta$.
$30\eta$.
Table 4. Scaling exponents for the longitudinal structure functions of even orders up to ![]() $p=12$ calculated using the direct and the ESS methods. Comparison of the present work with the results from Camussi et al. (Reference Camussi, Barbagallo, Guj and Stella1996), Zhou & Antonia (Reference Zhou and Antonia2000), Boratav & Pelz (Reference Boratav and Pelz1997) and Iyer et al. (Reference Iyer, Sreenivasan and Yeung2017).
$p=12$ calculated using the direct and the ESS methods. Comparison of the present work with the results from Camussi et al. (Reference Camussi, Barbagallo, Guj and Stella1996), Zhou & Antonia (Reference Zhou and Antonia2000), Boratav & Pelz (Reference Boratav and Pelz1997) and Iyer et al. (Reference Iyer, Sreenivasan and Yeung2017).
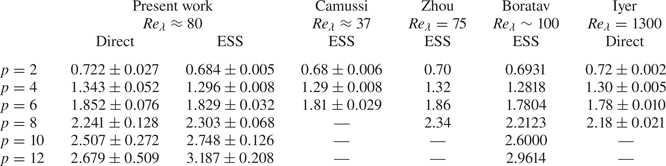
Figure 19(a) shows scaling exponents ![]() $\xi _{g}^{p}$ and
$\xi _{g}^{p}$ and ![]() $\xi _{t}^{p}$ computed using the ESS method, compared to the original predictions by Kolmogorov (Reference Kolmogorov1941, KM41) extended to
$\xi _{t}^{p}$ computed using the ESS method, compared to the original predictions by Kolmogorov (Reference Kolmogorov1941, KM41) extended to ![]() $p > 3$, the refined similarity hypotheses of Kolmogorov (Reference Kolmogorov1962, KM62), the intermittency
$p > 3$, the refined similarity hypotheses of Kolmogorov (Reference Kolmogorov1962, KM62), the intermittency ![]() $\beta$ model by Frisch, Sulem & Nelkin (Reference Frisch, Sulem and Nelkin1978) and the model by She & Leveque (Reference She and Leveque1994). The transverse scaling exponents
$\beta$ model by Frisch, Sulem & Nelkin (Reference Frisch, Sulem and Nelkin1978) and the model by She & Leveque (Reference She and Leveque1994). The transverse scaling exponents ![]() $\xi _{t}^{p}$ in figure 19 are obtained by making
$\xi _{t}^{p}$ in figure 19 are obtained by making ![]() $\langle (\delta u_{t})^{p}\rangle$ depend on the magnitude of transverse velocity differences for
$\langle (\delta u_{t})^{p}\rangle$ depend on the magnitude of transverse velocity differences for ![]() $p = 3$ rather than the longitudinal, thus following the ESS method (Camussi et al. Reference Camussi, Barbagallo, Guj and Stella1996; Grossmann, Lohse & Reeh Reference Grossmann, Lohse and Reeh1997). The refined similarity hypotheses are found to hold, but there is a visible tendency of
$p = 3$ rather than the longitudinal, thus following the ESS method (Camussi et al. Reference Camussi, Barbagallo, Guj and Stella1996; Grossmann, Lohse & Reeh Reference Grossmann, Lohse and Reeh1997). The refined similarity hypotheses are found to hold, but there is a visible tendency of ![]() $\xi _{t}^{p}$ to deviate from the longitudinal scaling for
$\xi _{t}^{p}$ to deviate from the longitudinal scaling for ![]() $p \geqslant 4$. This is to be ascribed to the Reynolds number and the residual anisotropy of the flow, as argued by Iyer et al. (Reference Iyer, Sreenivasan and Yeung2017).
$p \geqslant 4$. This is to be ascribed to the Reynolds number and the residual anisotropy of the flow, as argued by Iyer et al. (Reference Iyer, Sreenivasan and Yeung2017).

Figure 19. (a) Scaling exponents ![]() $\xi _{g}^{p}$ and
$\xi _{g}^{p}$ and ![]() $\xi _{t}^{p}$ computed with the ESS method versus
$\xi _{t}^{p}$ computed with the ESS method versus ![]() $p$ for orders up to
$p$ for orders up to ![]() $20$ (
$20$ (![]() $x = 25$). In the same plot there are the results from different intermittency models assuming
$x = 25$). In the same plot there are the results from different intermittency models assuming ![]() $\mu = 0.08$:
$\mu = 0.08$: ![]() $\circ$,
$\circ$, ![]() $\xi _{g}^{p}$;
$\xi _{g}^{p}$; ![]() $\ast$,
$\ast$, ![]() $\xi _{t}^{p}$; solid line, KM41 model; dashed line, KM62 model; dot-dashed line,
$\xi _{t}^{p}$; solid line, KM41 model; dashed line, KM62 model; dot-dashed line, ![]() $\beta$ model; and dotted line, She–Leveque model. (b) Behaviours of the intermittency exponent along
$\beta$ model; and dotted line, She–Leveque model. (b) Behaviours of the intermittency exponent along ![]() $x$ computed according to two different methods: solid line, based on
$x$ computed according to two different methods: solid line, based on ![]() $\langle \epsilon (\boldsymbol {x}+\boldsymbol {r}) \epsilon (\boldsymbol {x}) \rangle /\langle \epsilon \rangle ^{2} \sim (L/r)^{\mu }$; and dotted line,
$\langle \epsilon (\boldsymbol {x}+\boldsymbol {r}) \epsilon (\boldsymbol {x}) \rangle /\langle \epsilon \rangle ^{2} \sim (L/r)^{\mu }$; and dotted line, ![]() $\mu = 2-\xi _{g}^{6}$.
$\mu = 2-\xi _{g}^{6}$.
Figure 19(b) displays the evolution of the intermittency exponent ![]() $\mu$ along the streamwise direction; the quantity defined in (3.20) is also employed in the
$\mu$ along the streamwise direction; the quantity defined in (3.20) is also employed in the ![]() $\beta$-model by Frisch et al. (Reference Frisch, Sulem and Nelkin1978). The
$\beta$-model by Frisch et al. (Reference Frisch, Sulem and Nelkin1978). The ![]() $\mu$ exponent is calculated directly from the slope of the correlation coefficient obtained by dividing the autocorrelation of dissipation by
$\mu$ exponent is calculated directly from the slope of the correlation coefficient obtained by dividing the autocorrelation of dissipation by ![]() $\langle \epsilon \rangle ^{2}$ for separations in the inertial range; see figure 20. A second possible way to obtain
$\langle \epsilon \rangle ^{2}$ for separations in the inertial range; see figure 20. A second possible way to obtain ![]() $\mu$ is by using the expression relating the longitudinal sixth-order moment to the autocorrelation of dissipation (Frisch et al. Reference Frisch, Sulem and Nelkin1978):
$\mu$ is by using the expression relating the longitudinal sixth-order moment to the autocorrelation of dissipation (Frisch et al. Reference Frisch, Sulem and Nelkin1978):
The two quantities are reported in figure 19(b). As the reference value reported in many studies for the intermittency exponent is ![]() $\mu = 0.25 \pm 0.05$, which is deemed to be valid for high-Reynolds-number flows (Pope Reference Pope2000), the values calculated here suggest that the effect generated by intermittent structures on small-scale turbulence in the moderate-Reynolds-number range is less intense than at high Reynolds numbers. It is noticed that the method based on sixth-order structure functions, (3.21), displays a decay in the
$\mu = 0.25 \pm 0.05$, which is deemed to be valid for high-Reynolds-number flows (Pope Reference Pope2000), the values calculated here suggest that the effect generated by intermittent structures on small-scale turbulence in the moderate-Reynolds-number range is less intense than at high Reynolds numbers. It is noticed that the method based on sixth-order structure functions, (3.21), displays a decay in the ![]() $x$-direction that is not expected nor recovered in the calculation of
$x$-direction that is not expected nor recovered in the calculation of ![]() $\mu$ directly from the definition (3.20).
$\mu$ directly from the definition (3.20).

Figure 20. Dissipation correlation coefficient at ![]() $x=25$: solid line,
$x=25$: solid line, ![]() $\langle \epsilon (\boldsymbol {x}+\boldsymbol {r}) \epsilon (\boldsymbol {x}) \rangle /\langle \epsilon \rangle ^{2}$ as calculated from its definition; and dot-dashed line,
$\langle \epsilon (\boldsymbol {x}+\boldsymbol {r}) \epsilon (\boldsymbol {x}) \rangle /\langle \epsilon \rangle ^{2}$ as calculated from its definition; and dot-dashed line, ![]() $a_{d}(r/\eta )^{d}$, where
$a_{d}(r/\eta )^{d}$, where ![]() $a_{d}=1.07$ and
$a_{d}=1.07$ and ![]() $d=-0.082$. The dashed lines delimit the interval used for the power-law fitting procedure,
$d=-0.082$. The dashed lines delimit the interval used for the power-law fitting procedure, ![]() $25\eta < r < 75\eta$, and the dotted lines demarcate the decorrelation scale
$25\eta < r < 75\eta$, and the dotted lines demarcate the decorrelation scale ![]() $\tilde {r}$.
$\tilde {r}$.
The decorrelation scale ![]() $\tilde {r}$ is defined as the length of decorrelation of the instantaneous dissipation
$\tilde {r}$ is defined as the length of decorrelation of the instantaneous dissipation ![]() $\epsilon$, i.e. the separation scale
$\epsilon$, i.e. the separation scale ![]() $r$ where
$r$ where ![]() $\langle \epsilon (\boldsymbol {x}+\boldsymbol {r}) \epsilon (\boldsymbol {x}) \rangle / \langle \epsilon \rangle ^{2}$ becomes unitary with a
$\langle \epsilon (\boldsymbol {x}+\boldsymbol {r}) \epsilon (\boldsymbol {x}) \rangle / \langle \epsilon \rangle ^{2}$ becomes unitary with a ![]() $1\,\%$ error. In figure 21 the development of
$1\,\%$ error. In figure 21 the development of ![]() $\tilde {r}$ along
$\tilde {r}$ along ![]() $x$ is compared to that of the integral scale
$x$ is compared to that of the integral scale ![]() $L$. The decorrelation scale can be considered as a very large length scale, which in homogeneous isotropic turbulence depends on the Reynolds number and also the intermittency characteristics of the flow.
$L$. The decorrelation scale can be considered as a very large length scale, which in homogeneous isotropic turbulence depends on the Reynolds number and also the intermittency characteristics of the flow.

Figure 21. Streamwise evolution of the decorrelation scale in comparison with the integral scale: solid line, ![]() $\tilde {r}$; and dashed line,
$\tilde {r}$; and dashed line, ![]() $L$. For
$L$. For ![]() $x=25$,
$x=25$, ![]() $\tilde {r}/\eta =135$ and
$\tilde {r}/\eta =135$ and ![]() $L/\eta =45$.
$L/\eta =45$.
3.10. Turbulent energy budgets
The equation governing the transport of ![]() $\langle k \rangle$ in a statistically steady case can be written in symbols as
$\langle k \rangle$ in a statistically steady case can be written in symbols as
where ![]() $\mathcal {A}$ is the contribution by mean advection and
$\mathcal {A}$ is the contribution by mean advection and ![]() $\mathcal {T}_{p}$,
$\mathcal {T}_{p}$, ![]() $\mathcal {T}_{t}$ and
$\mathcal {T}_{t}$ and ![]() $\mathcal {D}_{v}$ represent pressure, turbulent and diffusive transports;
$\mathcal {D}_{v}$ represent pressure, turbulent and diffusive transports; ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\langle \tilde {\epsilon }\rangle$ stand for the production and pseudo-dissipation rate of turbulent kinetic energy, defined as
$\langle \tilde {\epsilon }\rangle$ stand for the production and pseudo-dissipation rate of turbulent kinetic energy, defined as
As the difference ![]() $\langle \epsilon \rangle - \langle \tilde {\epsilon } \rangle$ is seldom important (Pope Reference Pope2000), in this section
$\langle \epsilon \rangle - \langle \tilde {\epsilon } \rangle$ is seldom important (Pope Reference Pope2000), in this section ![]() $\langle \epsilon \rangle$ is used.
$\langle \epsilon \rangle$ is used.
In grid turbulence cases, where mean velocity gradients are zero and cross-flow directions ![]() $y$ and
$y$ and ![]() $z$ are homogeneous, the production term vanishes:
$z$ are homogeneous, the production term vanishes:
In addition, for the Reynolds number computed here, the molecular contribution to transport is negligible. The resulting expression for the budget equation (3.22) thus becomes
 \begin{equation} \underbrace{ \langle U\rangle \frac{\textrm{d} \langle k \rangle}{\textrm{d}\kern0.9pt{x}}}_{-\mathcal{A}} = \underbrace{-\frac{\textrm{d}\langle u p\rangle}{\textrm{d}\kern0.9pt{x}}}_{\mathcal{T}_{p}} \underbrace{-\,\frac{\textrm{d}\langle u k\rangle}{\textrm{d}\kern0.9pt{x}}}_{\mathcal{T}_{t}} - \langle \tilde{\epsilon} \rangle , \end{equation}
\begin{equation} \underbrace{ \langle U\rangle \frac{\textrm{d} \langle k \rangle}{\textrm{d}\kern0.9pt{x}}}_{-\mathcal{A}} = \underbrace{-\frac{\textrm{d}\langle u p\rangle}{\textrm{d}\kern0.9pt{x}}}_{\mathcal{T}_{p}} \underbrace{-\,\frac{\textrm{d}\langle u k\rangle}{\textrm{d}\kern0.9pt{x}}}_{\mathcal{T}_{t}} - \langle \tilde{\epsilon} \rangle , \end{equation}
where the single terms are distributed along the ![]() $x$-axis as depicted in figure 22.
$x$-axis as depicted in figure 22.

Figure 22. Turbulent kinetic energy along the streamwise direction in logarithmic plots. In panel (a) budget terms are reported: solid line, ![]() $\mathcal {A}$; dot-dashed line,
$\mathcal {A}$; dot-dashed line, ![]() $\mathcal {T}_{p}$; dotted line,
$\mathcal {T}_{p}$; dotted line, ![]() $\mathcal {T}_{t}$; and dashed line,
$\mathcal {T}_{t}$; and dashed line, ![]() $-\langle \tilde {\epsilon } \rangle$. Panel (b) presents turbulent kinetic energy fluxes: solid line,
$-\langle \tilde {\epsilon } \rangle$. Panel (b) presents turbulent kinetic energy fluxes: solid line, ![]() $\langle U \rangle \langle k \rangle$; dot-dashed line,
$\langle U \rangle \langle k \rangle$; dot-dashed line, ![]() $\langle u p\rangle$; and dotted line,
$\langle u p\rangle$; and dotted line, ![]() $\langle u k\rangle$. The inset in (a) displays an enlargement of the budget terms in the range
$\langle u k\rangle$. The inset in (a) displays an enlargement of the budget terms in the range ![]() $I_d$ in linear scale.
$I_d$ in linear scale.
Two regions can be identified in figure 22: a near-field region where the three conservative terms redistribute the kinetic energy along ![]() $x$, and a far-field region where pressure and turbulent transports become negligible. Thus dissipation is solely balanced by turbulent kinetic energy advection; see figure 22(a) and its inset. A possible downstream boundary for the near-field region can be set at
$x$, and a far-field region where pressure and turbulent transports become negligible. Thus dissipation is solely balanced by turbulent kinetic energy advection; see figure 22(a) and its inset. A possible downstream boundary for the near-field region can be set at ![]() $x = 2$, where the turbulent and pressure transports become 100 times smaller than advection and dissipation.
$x = 2$, where the turbulent and pressure transports become 100 times smaller than advection and dissipation.
The near-field region can be subdivided into two subregions. By considering the ligament diameter ![]() $d_f$ as the length scale, a region very close to the metal foam is identified for
$d_f$ as the length scale, a region very close to the metal foam is identified for ![]() $x^\ast /d_f < 0.5$, where turbulent transport is larger than the advective one. This region is characterised by the sustainment of turbulence by means of streamwise fluctuations, which is counter-balanced by dissipation, as pressure and advective transports account for negligible shares. The second subregion extends for
$x^\ast /d_f < 0.5$, where turbulent transport is larger than the advective one. This region is characterised by the sustainment of turbulence by means of streamwise fluctuations, which is counter-balanced by dissipation, as pressure and advective transports account for negligible shares. The second subregion extends for ![]() $0.5 < x^\ast /d_f < 14$, where turbulent kinetic energy is provided through pressure and advective mechanisms while dissipation and turbulent transport drain
$0.5 < x^\ast /d_f < 14$, where turbulent kinetic energy is provided through pressure and advective mechanisms while dissipation and turbulent transport drain ![]() $\langle k \rangle$; see figure 22(a).
$\langle k \rangle$; see figure 22(a).
Data gathered by Norberg (Reference Norberg1998) indicate that the vortex formation length ![]() $\ell _f$ for the present Reynolds number based on the mean diameter of the filaments,
$\ell _f$ for the present Reynolds number based on the mean diameter of the filaments, ![]() ${\textit {Re}}_{d_f} = 560$, lies in the range
${\textit {Re}}_{d_f} = 560$, lies in the range ![]() $1.5 d_f < \ell _f < 2 d_f$; see Bloor, Gerrard & Lighthill (Reference Bloor, Gerrard and Lighthill1966) for other possible definitions of the vortex formation length. Figure 22(a) displays that this range matches the streamwise location where all the transport terms in (3.25) peak. Therefore, the present data suggest that kinetic energy is originated in the second part of the near-field region, where transport mechanisms show local peaks. Turbulent kinetic energy
$1.5 d_f < \ell _f < 2 d_f$; see Bloor, Gerrard & Lighthill (Reference Bloor, Gerrard and Lighthill1966) for other possible definitions of the vortex formation length. Figure 22(a) displays that this range matches the streamwise location where all the transport terms in (3.25) peak. Therefore, the present data suggest that kinetic energy is originated in the second part of the near-field region, where transport mechanisms show local peaks. Turbulent kinetic energy ![]() $\langle k \rangle$ is drained from here by the turbulent transport, which transfers turbulent fluctuations upstream, as indicated by the negative sign of the turbulent flux (see figure 22b), feeding the region very close to the metal foam. On the other hand, pressure and advective mechanisms are found to provide turbulent kinetic energy in the entire region
$\langle k \rangle$ is drained from here by the turbulent transport, which transfers turbulent fluctuations upstream, as indicated by the negative sign of the turbulent flux (see figure 22b), feeding the region very close to the metal foam. On the other hand, pressure and advective mechanisms are found to provide turbulent kinetic energy in the entire region ![]() $0.5 < x^\ast /d_f < 14$, and the signs of the relative fluxes indicate that velocity fluctuations are transferred downstream. At the coordinate
$0.5 < x^\ast /d_f < 14$, and the signs of the relative fluxes indicate that velocity fluctuations are transferred downstream. At the coordinate ![]() $x^\ast /d_f=14$ (
$x^\ast /d_f=14$ (![]() $x=2$), fluxes
$x=2$), fluxes ![]() $\langle u p\rangle$ and
$\langle u p\rangle$ and ![]() $\langle u k\rangle$ become constant in the streamwise direction, leading to the budget reported in (3.4) for
$\langle u k\rangle$ become constant in the streamwise direction, leading to the budget reported in (3.4) for ![]() $x>2$, which is typical in developed decaying flows; see figure 22(a) and its inset, which reports the budget terms in the
$x>2$, which is typical in developed decaying flows; see figure 22(a) and its inset, which reports the budget terms in the ![]() $I_d$ region.
$I_d$ region.
In order to separately assess the behaviour of streamwise and cross-flow velocity fluctuations, the transport equations for velocity variances are analysed. The budget of streamwise velocity variance reads
 \begin{equation} \underbrace{ \langle U \rangle \frac{\textrm{d} \langle u^{2} \rangle}{\textrm{d}\kern0.9pt{x}}}_{-\mathcal{A}^u} = \underbrace{- \frac{\textrm{d} \langle u^{3} \rangle}{ {\textrm{d}\kern0.9pt{x}}}}_{\mathcal{T}_{t}^u} \underbrace{-\,2\frac{\textrm{d} \langle u p \rangle}{ {\textrm{d}\kern0.9pt{x}}}}_{\mathcal{T}_{p}^u} \underbrace{+\,2\left\langle p \,\frac{\partial u}{\partial x} \right\rangle}_{\mathcal{S}^u} - \langle \widetilde{\epsilon_u} \rangle, \end{equation}
\begin{equation} \underbrace{ \langle U \rangle \frac{\textrm{d} \langle u^{2} \rangle}{\textrm{d}\kern0.9pt{x}}}_{-\mathcal{A}^u} = \underbrace{- \frac{\textrm{d} \langle u^{3} \rangle}{ {\textrm{d}\kern0.9pt{x}}}}_{\mathcal{T}_{t}^u} \underbrace{-\,2\frac{\textrm{d} \langle u p \rangle}{ {\textrm{d}\kern0.9pt{x}}}}_{\mathcal{T}_{p}^u} \underbrace{+\,2\left\langle p \,\frac{\partial u}{\partial x} \right\rangle}_{\mathcal{S}^u} - \langle \widetilde{\epsilon_u} \rangle, \end{equation}
where, from left to right, the first three terms, respectively, represent the advective, turbulent and pressure transports of ![]() $\langle u^2 \rangle$,
$\langle u^2 \rangle$, ![]() $\langle p \partial u/\partial x \rangle$ is the pressure strain term and
$\langle p \partial u/\partial x \rangle$ is the pressure strain term and ![]() $\widetilde {\epsilon _u}$ stands for the
$\widetilde {\epsilon _u}$ stands for the ![]() $u$-variance pseudo-dissipation rate,
$u$-variance pseudo-dissipation rate, ![]() $\widetilde {\epsilon _u} = 2 ((\partial u/\partial x_j) \, (\partial u/\partial x_j)) / {\textit {Re}}_{d_p}$. The diffusive transport is again neglected with respect to the other terms. Equations similar to (3.26) can be derived for the transverse velocity components,
$\widetilde {\epsilon _u} = 2 ((\partial u/\partial x_j) \, (\partial u/\partial x_j)) / {\textit {Re}}_{d_p}$. The diffusive transport is again neglected with respect to the other terms. Equations similar to (3.26) can be derived for the transverse velocity components, ![]() $v$ and
$v$ and ![]() $w$. As the flow is isotropic on
$w$. As the flow is isotropic on ![]() $y$–
$y$–![]() $z$ planes, statistics for the transverse velocity component are obtained by averaging results along
$z$ planes, statistics for the transverse velocity component are obtained by averaging results along ![]() $y$ and
$y$ and ![]() $z$. For conciseness, the transverse velocity component is indicated by
$z$. For conciseness, the transverse velocity component is indicated by ![]() $v$ and its direction by
$v$ and its direction by ![]() $y$,
$y$,
 \begin{equation} \underbrace{ \langle U \rangle \frac{\textrm{d} \langle v^{2} \rangle}{\textrm{d}\kern0.9pt{x}}}_{-\mathcal{A}^v} = \underbrace{- \frac{\textrm{d} \langle u v^{2} \rangle}{ {\textrm{d}\kern0.9pt{x}}}}_{\mathcal{T}_{t}^v} \underbrace{+\,2\left\langle p\, \frac{\partial v}{\partial y} \right\rangle}_{\mathcal{S}^v} - \langle \widetilde{\epsilon_v} \rangle, \end{equation}
\begin{equation} \underbrace{ \langle U \rangle \frac{\textrm{d} \langle v^{2} \rangle}{\textrm{d}\kern0.9pt{x}}}_{-\mathcal{A}^v} = \underbrace{- \frac{\textrm{d} \langle u v^{2} \rangle}{ {\textrm{d}\kern0.9pt{x}}}}_{\mathcal{T}_{t}^v} \underbrace{+\,2\left\langle p\, \frac{\partial v}{\partial y} \right\rangle}_{\mathcal{S}^v} - \langle \widetilde{\epsilon_v} \rangle, \end{equation}
where the terms have the same interpretation as in (3.26), and the pseudo-dissipation rate of the ![]() $v$-variance is computed as
$v$-variance is computed as ![]() $\widetilde {\epsilon _v} = 2 ((\partial v/\partial x_j) \, (\partial v/\partial x_j)) / {\textit {Re}}_{d_p}$. Note that, with respect to equation (3.25), budgets of velocity component variances include the pressure strain terms. As will be shown in the following, the role of these terms is to redistribute kinetic energy among the velocity components and thus it is responsible for the ‘return to isotropy’ in homogeneous turbulence. Such a phenomenon has been studied for several decades as it is involved in second-order turbulence models; see, for example, the works by Rotta (Reference Rotta1951) and Lumley & Newman (Reference Lumley and Newman1977). Pressure strain terms are not included in (3.25) as their sum
$\widetilde {\epsilon _v} = 2 ((\partial v/\partial x_j) \, (\partial v/\partial x_j)) / {\textit {Re}}_{d_p}$. Note that, with respect to equation (3.25), budgets of velocity component variances include the pressure strain terms. As will be shown in the following, the role of these terms is to redistribute kinetic energy among the velocity components and thus it is responsible for the ‘return to isotropy’ in homogeneous turbulence. Such a phenomenon has been studied for several decades as it is involved in second-order turbulence models; see, for example, the works by Rotta (Reference Rotta1951) and Lumley & Newman (Reference Lumley and Newman1977). Pressure strain terms are not included in (3.25) as their sum ![]() $\mathcal {S}^u + 2\mathcal {S}^v$ vanishes because of incompressibility.
$\mathcal {S}^u + 2\mathcal {S}^v$ vanishes because of incompressibility.
Figures 23 and 24 show the velocity variance budgets and fluxes along the streamwise coordinate. It appears that transport mechanisms are more intense in the ![]() $\langle u^2\rangle$ budget with respect to
$\langle u^2\rangle$ budget with respect to ![]() $\langle v^2\rangle$, while dissipations
$\langle v^2\rangle$, while dissipations ![]() $\langle \widetilde {\epsilon _u}\rangle$ and
$\langle \widetilde {\epsilon _u}\rangle$ and ![]() $\langle \widetilde {\epsilon _v}\rangle$ are almost equal. The behaviour of the pressure strain terms reveals that turbulent energy is drained from the streamwise velocity fluctuations, as
$\langle \widetilde {\epsilon _v}\rangle$ are almost equal. The behaviour of the pressure strain terms reveals that turbulent energy is drained from the streamwise velocity fluctuations, as ![]() $\mathcal {S}^u$ represents a sink term in the
$\mathcal {S}^u$ represents a sink term in the ![]() $\langle u^2\rangle$ budget, and provided to cross-flow velocity fluctuations, where
$\langle u^2\rangle$ budget, and provided to cross-flow velocity fluctuations, where ![]() $\mathcal {S}^v$ acts as a source; see figures 23(a) and 24(a). The role of
$\mathcal {S}^v$ acts as a source; see figures 23(a) and 24(a). The role of ![]() $\mathcal {S}^u$ and
$\mathcal {S}^u$ and ![]() $\mathcal {S}^v$ does not change along the whole streamwise extension of the domain, as shown by the insets in figures 23(a) and 24(a). This occurs because, as reported in § 3.2, flow anisotropy is conserved in the flow domain considered. In the decaying region
$\mathcal {S}^v$ does not change along the whole streamwise extension of the domain, as shown by the insets in figures 23(a) and 24(a). This occurs because, as reported in § 3.2, flow anisotropy is conserved in the flow domain considered. In the decaying region ![]() $I_d$, the pressure strain terms maintain an intensity comparable to the advective and dissipation terms, suggesting that the isotropic condition would have been reached in a longer computational domain.
$I_d$, the pressure strain terms maintain an intensity comparable to the advective and dissipation terms, suggesting that the isotropic condition would have been reached in a longer computational domain.

Figure 23. Variance of streamwise velocity component along the streamwise direction in logarithmic plots. In panel (a) budget terms are reported: solid line, ![]() $\mathcal {A}^u$; dotted line,
$\mathcal {A}^u$; dotted line, ![]() $\mathcal {T}_{t}^u$; dot-dashed line,
$\mathcal {T}_{t}^u$; dot-dashed line, ![]() $\mathcal {T}_{p}^u$; solid line with circles,
$\mathcal {T}_{p}^u$; solid line with circles, ![]() $\mathcal {S}^u$; and dashed line,
$\mathcal {S}^u$; and dashed line, ![]() $-\langle \widetilde {\epsilon _u} \rangle$. Panel (b) presents
$-\langle \widetilde {\epsilon _u} \rangle$. Panel (b) presents ![]() $\langle u^2 \rangle$ fluxes: solid line,
$\langle u^2 \rangle$ fluxes: solid line, ![]() $\langle U \rangle \langle u^2 \rangle$; dot-dashed line,
$\langle U \rangle \langle u^2 \rangle$; dot-dashed line, ![]() $\langle u p\rangle$; and dotted line,
$\langle u p\rangle$; and dotted line, ![]() $\langle u^3\rangle$. The inset in (a) displays an enlargement of the budget terms in the range
$\langle u^3\rangle$. The inset in (a) displays an enlargement of the budget terms in the range ![]() $I_d$ in linear scale.
$I_d$ in linear scale.

Figure 24. Variance of cross-flow velocity component along the streamwise direction in logarithmic plots. In panel (a) budget terms are reported: solid line, ![]() $\mathcal {A}^v$; dotted line,
$\mathcal {A}^v$; dotted line, ![]() $\mathcal {T}_{t}^v$; solid line with circles,
$\mathcal {T}_{t}^v$; solid line with circles, ![]() $\mathcal {S}^v$; and dashed line,
$\mathcal {S}^v$; and dashed line, ![]() $-\langle \widetilde {\epsilon _v} \rangle$. Panel (b) presents
$-\langle \widetilde {\epsilon _v} \rangle$. Panel (b) presents ![]() $\langle v^2 \rangle$ fluxes: solid line,
$\langle v^2 \rangle$ fluxes: solid line, ![]() $\langle U \rangle \langle v^2 \rangle$; and dotted line,
$\langle U \rangle \langle v^2 \rangle$; and dotted line, ![]() $\langle uv^2\rangle$. The inset in (a) displays an enlargement of the budget terms in the range
$\langle uv^2\rangle$. The inset in (a) displays an enlargement of the budget terms in the range ![]() $I_d$ in linear scale.
$I_d$ in linear scale.
The profiles in figures 23 and 24 show that the ![]() $u$-variance terms behave very similarly to the budgets and fluxes of turbulent kinetic energy reported in figure 22. In particular, the peaks of turbulent, advective and pressure transports are located at the same distance from the metal foam, comparable to the vortex formation length. This suggests that velocity fluctuations are more intensely triggered along the streamwise direction with respect to the transverse ones. On the other hand, the
$u$-variance terms behave very similarly to the budgets and fluxes of turbulent kinetic energy reported in figure 22. In particular, the peaks of turbulent, advective and pressure transports are located at the same distance from the metal foam, comparable to the vortex formation length. This suggests that velocity fluctuations are more intensely triggered along the streamwise direction with respect to the transverse ones. On the other hand, the ![]() $v$-variance terms peak slightly downstream with respect to terms in the
$v$-variance terms peak slightly downstream with respect to terms in the ![]() $\langle u^2 \rangle$ and
$\langle u^2 \rangle$ and ![]() $\langle k \rangle$ budgets, and the negative peak of turbulent transport is not very intense (see figure 24a), but it drains enough energy to sustain cross-flow fluctuations in the region just downstream of the metal foam. Another difference with respect to the
$\langle k \rangle$ budgets, and the negative peak of turbulent transport is not very intense (see figure 24a), but it drains enough energy to sustain cross-flow fluctuations in the region just downstream of the metal foam. Another difference with respect to the ![]() $\langle u^2 \rangle$ terms is the positive – yet not that intense – turbulent flux very close to the metal foam, indicating that cross-flow fluctuations are more correlated with positive
$\langle u^2 \rangle$ terms is the positive – yet not that intense – turbulent flux very close to the metal foam, indicating that cross-flow fluctuations are more correlated with positive ![]() $u$-fluctuations in this region (see figure 24b).
$u$-fluctuations in this region (see figure 24b).
4. Conclusions
An analysis is presented of the turbulent flow behind a synthetic metal foam layer of thickness equal to five times the mean pore diameter. Unlike classical grid turbulence geometries, the metal foam ligaments are variably oriented, unevenly spaced and in general less ordered. Similar to classical grids, metal foams are mainly characterised by two length scales i.e. the pore diameter and the ligament thickness. The analysis encompasses one single Reynolds number ![]() ${\textit {Re}}_{d_p} = 4000$ and
${\textit {Re}}_{d_p} = 4000$ and ![]() $\varepsilon = 0.92$ but the effect of a different porosity (
$\varepsilon = 0.92$ but the effect of a different porosity (![]() $\varepsilon = 0.97$) on selected quantities is addressed in the Appendix.
$\varepsilon = 0.97$) on selected quantities is addressed in the Appendix.
The analysis of the turbulent kinetic energy budget suggests that turbulence is triggered in the region close to the metal foam, approximately at a distance equal to the vortex formation length indicated by Norberg (Reference Norberg1998), ![]() $x^\ast /d_f \approx 2$. In the near-field region,
$x^\ast /d_f \approx 2$. In the near-field region, ![]() $x<2$, turbulent kinetic energy is distributed by transport mechanisms; the turbulent transport moves
$x<2$, turbulent kinetic energy is distributed by transport mechanisms; the turbulent transport moves ![]() $\langle k \rangle$ upstream, sustaining fluctuations in close proximity to the metal foam, while pressure and advective transports provide velocity fluctuations to larger
$\langle k \rangle$ upstream, sustaining fluctuations in close proximity to the metal foam, while pressure and advective transports provide velocity fluctuations to larger ![]() $x$-coordinates. At
$x$-coordinates. At ![]() $x=2$, pressure and turbulent transports are found to be negligible with respect to the other terms, entailing for
$x=2$, pressure and turbulent transports are found to be negligible with respect to the other terms, entailing for ![]() $x>2$ the expected behaviour of grid turbulence, where viscous dissipation is balanced by the mean advection of
$x>2$ the expected behaviour of grid turbulence, where viscous dissipation is balanced by the mean advection of ![]() $\langle k \rangle$. Budgets of streamwise and cross-flow velocity variances indicate that fluctuations along
$\langle k \rangle$. Budgets of streamwise and cross-flow velocity variances indicate that fluctuations along ![]() $x$ are the most intensely triggered and pressure strain terms act to redistribute turbulent energy towards the isotropic condition, which however is not observed due to the limited domain extension.
$x$ are the most intensely triggered and pressure strain terms act to redistribute turbulent energy towards the isotropic condition, which however is not observed due to the limited domain extension.
In that same near-field region, ![]() ${\textit {Re}}_\lambda$ decreases steeply and the dissipation rate coefficient
${\textit {Re}}_\lambda$ decreases steeply and the dissipation rate coefficient ![]() $C_\epsilon$ approximates
$C_\epsilon$ approximates ![]() $C_\epsilon \propto {\textit {Re}}_\lambda ^{-1}$ while
$C_\epsilon \propto {\textit {Re}}_\lambda ^{-1}$ while ![]() $L/\lambda$ remains almost constant. These observations, in conjunction with the typical
$L/\lambda$ remains almost constant. These observations, in conjunction with the typical ![]() $- 5/3$ slope in the turbulent power spectra, represent a typical behaviour already observed in the literature (Valente & Vassilicos Reference Valente and Vassilicos2012). Given that this occurs very close to the porous matrix, where the hypotheses for the Richardson cascade are not verified, a considerable variation in
$- 5/3$ slope in the turbulent power spectra, represent a typical behaviour already observed in the literature (Valente & Vassilicos Reference Valente and Vassilicos2012). Given that this occurs very close to the porous matrix, where the hypotheses for the Richardson cascade are not verified, a considerable variation in ![]() $C_\epsilon$ is not interpreted here as an anomalous behaviour.
$C_\epsilon$ is not interpreted here as an anomalous behaviour.
The developed region is defined here as the region where ![]() $u_{rms}$ decays following a power law and starts at
$u_{rms}$ decays following a power law and starts at ![]() $x_{min} = 7.98$. Besides
$x_{min} = 7.98$. Besides ![]() $\langle k \rangle$, a number of relevant quantities, like the integral length scale, the Taylor microscale and the Kolmogorov scale of the flow, are observed to follow a power-law behaviour. The exponents obtained from a least-squares fit are in many cases very close to values predicted and measured in classical grid turbulence experiments. Given
$\langle k \rangle$, a number of relevant quantities, like the integral length scale, the Taylor microscale and the Kolmogorov scale of the flow, are observed to follow a power-law behaviour. The exponents obtained from a least-squares fit are in many cases very close to values predicted and measured in classical grid turbulence experiments. Given ![]() $n_k = 1.14$ and
$n_k = 1.14$ and ![]() $q = 0.52$ (where
$q = 0.52$ (where ![]() $n_k$ and
$n_k$ and ![]() $q$ are the exponents of the power laws for
$q$ are the exponents of the power laws for ![]() $\langle k \rangle$ and
$\langle k \rangle$ and ![]() $L$), the constancy of
$L$), the constancy of ![]() $u_{rms}^2 L^3$ does not hold in the developed region simulated here, and thus the turbulence does not follow the theory by Saffman.
$u_{rms}^2 L^3$ does not hold in the developed region simulated here, and thus the turbulence does not follow the theory by Saffman.
Structure functions of different orders are calculated at a fixed position ![]() $x = 25$ in the fully developed region. The extended self-similarity is used to calculate the scaling exponents. The results are interpreted in the light of the refined similarity hypothesis. The intermittency exponent
$x = 25$ in the fully developed region. The extended self-similarity is used to calculate the scaling exponents. The results are interpreted in the light of the refined similarity hypothesis. The intermittency exponent ![]() $\mu$ computed directly from its definition is seen to behave uniformly within the computational domain. It reveals that intermittency is not very intense at the moderate Reynolds number of this study. The decorrelation length of dissipation
$\mu$ computed directly from its definition is seen to behave uniformly within the computational domain. It reveals that intermittency is not very intense at the moderate Reynolds number of this study. The decorrelation length of dissipation ![]() $\tilde {r}$ is larger than the integral scale. It depends on the Reynolds number as well as the intermittency characteristics of the flow.
$\tilde {r}$ is larger than the integral scale. It depends on the Reynolds number as well as the intermittency characteristics of the flow.
Acknowledgements
The authors would like to thank S. Chibbaro and A. Cimarelli for fruitful discussions and suggestions.
Funding
The authors acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and support.
Declaration of interests
The authors report no conflict of interest.
Appendix. A glance at the effect of porosity
The aim of this appendix is to verify the extent to which turbulent flow statistics in the lee of an open-cell metal foam layer are affected by porosity. The results obtained for a foam of porosity ![]() $\varepsilon =0.97$ are compared here against the
$\varepsilon =0.97$ are compared here against the ![]() $\varepsilon =0.92$ case, as investigated in the main body of the paper. The two foams have equal pore size but different ligament thickness, i.e. the foam with larger porosity is characterised by a thinner ligament,
$\varepsilon =0.92$ case, as investigated in the main body of the paper. The two foams have equal pore size but different ligament thickness, i.e. the foam with larger porosity is characterised by a thinner ligament, ![]() $d^{\prime }_f < d_f$. The comparison is conducted by means of DNS performed with the same numerical parameters as outlined in § 2 except for the computational grid, which consists of
$d^{\prime }_f < d_f$. The comparison is conducted by means of DNS performed with the same numerical parameters as outlined in § 2 except for the computational grid, which consists of ![]() $n_x = 2049$ and
$n_x = 2049$ and ![]() $n_y = n_z = 512$ grid nodes.
$n_y = n_z = 512$ grid nodes.
The porous matrix of higher porosity generates a turbulent field where fluctuations are less intense in all the spatial directions. Application of the fitting procedure outlined in § 3.3 on the high-porosity foam provides decay exponents for ![]() $u_{rms}^2$ and
$u_{rms}^2$ and ![]() $\langle k \rangle$ of
$\langle k \rangle$ of ![]() $n^{\prime }_u = 1.05$ and
$n^{\prime }_u = 1.05$ and ![]() $n^{\prime }_k = 1.08$, respectively. The results obtained on the coarse grid for the
$n^{\prime }_k = 1.08$, respectively. The results obtained on the coarse grid for the ![]() $\varepsilon =0.92$ case yield
$\varepsilon =0.92$ case yield ![]() $n_u = 1.12$ and
$n_u = 1.12$ and ![]() $n_k = 1.13$; see table 2 for comparisons against results on the fine mesh. The power-law decay of the turbulent kinetic energy begins more upstream than in the
$n_k = 1.13$; see table 2 for comparisons against results on the fine mesh. The power-law decay of the turbulent kinetic energy begins more upstream than in the ![]() $\varepsilon =0.92$ case; see figure 25.
$\varepsilon =0.92$ case; see figure 25.

Figure 25. Streamwise evolution of velocity fluctuations and turbulent kinetic energy for the ![]() $\varepsilon =0.97$ and
$\varepsilon =0.97$ and ![]() $\varepsilon =0.92$ cases on the coarse computational grid: solid line,
$\varepsilon =0.92$ cases on the coarse computational grid: solid line, ![]() $\langle uu\rangle$; dot-dashed line,
$\langle uu\rangle$; dot-dashed line, ![]() $\langle vv\rangle$; dotted line,
$\langle vv\rangle$; dotted line, ![]() $\langle ww\rangle$; and dashed line,
$\langle ww\rangle$; and dashed line, ![]() $\langle k \rangle$. The lines with circles mark the case with higher porosity
$\langle k \rangle$. The lines with circles mark the case with higher porosity ![]() $\varepsilon =0.97$.
$\varepsilon =0.97$.
Inside the developed region, the Kolmogorov and the longitudinal integral length scales evaluated for ![]() $\varepsilon =0.97$ behave according to power laws with growing rates estimated by the exponents
$\varepsilon =0.97$ behave according to power laws with growing rates estimated by the exponents ![]() $s^{\prime }=0.54$ and
$s^{\prime }=0.54$ and ![]() $q^{\prime }=0.47$, respectively (see table 3 for notation). The lower-porosity case exhibits decay exponents along the
$q^{\prime }=0.47$, respectively (see table 3 for notation). The lower-porosity case exhibits decay exponents along the ![]() $x$-direction of
$x$-direction of ![]() $s=0.56$ and
$s=0.56$ and ![]() $q=0.51$ (see table 3 for comparisons against results on the fine mesh) but the Kolmogorov and the integral scales are different in magnitude, as displayed by figure 26(a) and (b). Associated with the smaller kinetic energy content of the flow and a smaller dissipation rate observed at
$q=0.51$ (see table 3 for comparisons against results on the fine mesh) but the Kolmogorov and the integral scales are different in magnitude, as displayed by figure 26(a) and (b). Associated with the smaller kinetic energy content of the flow and a smaller dissipation rate observed at ![]() $\varepsilon =0.97$, the turbulence induced by the higher-porosity foam is characterised by a larger Kolmogorov scale and a smaller integral scale.
$\varepsilon =0.97$, the turbulence induced by the higher-porosity foam is characterised by a larger Kolmogorov scale and a smaller integral scale.

Figure 26. Comparison between the streamwise distributions of the Kolmogorov scale (a) and the longitudinal integral scale (b) for the ![]() $\varepsilon =0.97$ and
$\varepsilon =0.97$ and ![]() $\varepsilon =0.92$ cases on the coarse computational grid: solid line, length scales for
$\varepsilon =0.92$ cases on the coarse computational grid: solid line, length scales for ![]() $\varepsilon =0.92$; and solid line with circles, length scales for
$\varepsilon =0.92$; and solid line with circles, length scales for ![]() $\varepsilon =0.97$.
$\varepsilon =0.97$.
Figure 27 displays the effects of porosity on the terms of the turbulent kinetic energy budget. The transport mechanisms of ![]() $\langle k \rangle$ for
$\langle k \rangle$ for ![]() $\varepsilon =0.97$ are the same as described in § 3.10 for
$\varepsilon =0.97$ are the same as described in § 3.10 for ![]() $\varepsilon =0.92$ but are characterised by an upstream shift of the transport peaks with respect to that case. This shift is consistent with the reduction of the vortex formation length associated with a smaller ligament thickness, as indicated by Norberg (Reference Norberg1998) and reported in § 3.10.
$\varepsilon =0.92$ but are characterised by an upstream shift of the transport peaks with respect to that case. This shift is consistent with the reduction of the vortex formation length associated with a smaller ligament thickness, as indicated by Norberg (Reference Norberg1998) and reported in § 3.10.

Figure 27. Comparison between the turbulent kinetic energy budget terms for the ![]() $\varepsilon =0.97$ and
$\varepsilon =0.97$ and ![]() $\varepsilon =0.92$ cases on the coarse computational grid: solid line,
$\varepsilon =0.92$ cases on the coarse computational grid: solid line, ![]() $\mathcal {A}$; dot-dashed line,
$\mathcal {A}$; dot-dashed line, ![]() $\mathcal {T}_{p}$; dotted line,
$\mathcal {T}_{p}$; dotted line, ![]() $\mathcal {T}_{t}$; and dashed line,
$\mathcal {T}_{t}$; and dashed line, ![]() $-\langle \tilde {\epsilon }\rangle$. The lines with circles mark the case with higher porosity
$-\langle \tilde {\epsilon }\rangle$. The lines with circles mark the case with higher porosity ![]() $\varepsilon =0.97$.
$\varepsilon =0.97$.
In summary, while the results obtained for ![]() $\varepsilon =0.92$ show small quantitative differences with respect to
$\varepsilon =0.92$ show small quantitative differences with respect to ![]() $\varepsilon =0.97$, no significant discrepancies are observed between the two cases. An upstream shift in the peaks of
$\varepsilon =0.97$, no significant discrepancies are observed between the two cases. An upstream shift in the peaks of ![]() $\langle k \rangle$ transports characterises the higher-porosity case, which in turn implies a reduced vortex formation length and the achievement of power-law decays at shorter distances from the porous matrix. The size of such displacement is apparently very small.
$\langle k \rangle$ transports characterises the higher-porosity case, which in turn implies a reduced vortex formation length and the achievement of power-law decays at shorter distances from the porous matrix. The size of such displacement is apparently very small.

























































































































































































































