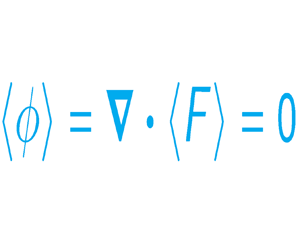1. Introduction
The velocity gradients, i.e. spatial derivatives of the velocity field, ![]() $\boldsymbol{\mathsf{A}} = \boldsymbol {\nabla }\boldsymbol {u}$, contain a wealth of information about small-scale turbulence, including the topology of vorticity and strain (Meneveau Reference Meneveau2011). The moments of the velocity gradients of an incompressible and statistically homogeneous field obey exact kinematic relations (Betchov Reference Betchov1956). The two so-called Betchov constraints for the velocity gradient principal invariants, namely the matrix traces
$\boldsymbol{\mathsf{A}} = \boldsymbol {\nabla }\boldsymbol {u}$, contain a wealth of information about small-scale turbulence, including the topology of vorticity and strain (Meneveau Reference Meneveau2011). The moments of the velocity gradients of an incompressible and statistically homogeneous field obey exact kinematic relations (Betchov Reference Betchov1956). The two so-called Betchov constraints for the velocity gradient principal invariants, namely the matrix traces ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}}^2)$ and
$\textrm {Tr}(\boldsymbol{\mathsf{A}}^2)$ and ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}}^3)$, are of central importance for a statistical description of the turbulent dynamics (Davidson Reference Davidson2004). The first Betchov constraint states that the second principal invariant of the velocity gradient is on average zero,
$\textrm {Tr}(\boldsymbol{\mathsf{A}}^3)$, are of central importance for a statistical description of the turbulent dynamics (Davidson Reference Davidson2004). The first Betchov constraint states that the second principal invariant of the velocity gradient is on average zero, ![]() $\langle \textrm {Tr}(\boldsymbol{\mathsf{A}}^2) \rangle =0$, which implies the proportionality between the mean dissipation rate and the mean squared vorticity:
$\langle \textrm {Tr}(\boldsymbol{\mathsf{A}}^2) \rangle =0$, which implies the proportionality between the mean dissipation rate and the mean squared vorticity:
Here ![]() $\nu$ is the kinematic viscosity of the fluid,
$\nu$ is the kinematic viscosity of the fluid, ![]() $\varepsilon = 2\nu \langle \textrm {Tr}(\boldsymbol{\mathsf{S}}^2) \rangle$ is the mean dissipation rate,
$\varepsilon = 2\nu \langle \textrm {Tr}(\boldsymbol{\mathsf{S}}^2) \rangle$ is the mean dissipation rate, ![]() $\boldsymbol{\mathsf{S}}$ is the strain rate and
$\boldsymbol{\mathsf{S}}$ is the strain rate and ![]() $\boldsymbol {\omega }=\boldsymbol {\nabla }\times \boldsymbol {u}$ is the vorticity. The second Betchov relation
$\boldsymbol {\omega }=\boldsymbol {\nabla }\times \boldsymbol {u}$ is the vorticity. The second Betchov relation ![]() $\langle \textrm {Tr}(\boldsymbol{\mathsf{A}}^3) \rangle =0$ connects strain self-amplification and vortex stretching:
$\langle \textrm {Tr}(\boldsymbol{\mathsf{A}}^3) \rangle =0$ connects strain self-amplification and vortex stretching:
While (1.1) constrains the strain-rate and vorticity magnitudes, (1.2) constrains their production rates. The latter relation was derived first by Townsend & Taylor (Reference Townsend and Taylor1951) and then rederived and extensively used by Betchov (Reference Betchov1956). It allows one to characterize the average turbulent energy cascade in physical space (Davidson Reference Davidson2004; Carbone & Bragg Reference Carbone and Bragg2020; Johnson Reference Johnson2020) and to predict the preferential configuration of the strain-rate eigenvalues (Betchov Reference Betchov1956). It also implies that vortex stretching has a positive average in the presence of an average forward energy cascade, related to the negative skewness of the longitudinal velocity increment and gradient statistics. This positive average has implications, for example, on the vorticity magnitude and orientation relative to the strain rate (Tsinober Reference Tsinober2009; Tom, Carbone & Bragg Reference Tom, Carbone and Bragg2021) and on the attenuation of extreme velocity gradients (Buaria, Pumir & Bodenschatz Reference Buaria, Pumir and Bodenschatz2020).
Additionally, relations (1.1) and (1.2) have their analogues for the velocity structure functions (Hill Reference Hill1997). The relations for the velocity structure functions are related to those for the velocity gradients through a simple Taylor expansion at small scales, and at larger scales through a filtered/perceived velocity gradient corrected for compressible effects (Carbone & Bragg Reference Carbone and Bragg2020). The compressible/perceived gradients in homogeneous turbulence also follow analogous relations (Yang, Pumir & Xu Reference Yang, Pumir and Xu2020; Yang et al. Reference Yang, Fang, Fang, Pumir and Xu2022), which, for example, constrain the dynamics of velocity gradients as perceived by Lagrangian tetrads (Chertkov, Pumir & Shraiman Reference Chertkov, Pumir and Shraiman1999; Xu, Pumir & Bodenschatz Reference Xu, Pumir and Bodenschatz2011).
Applications of the homogeneity relations (1.1) and (1.2) are not limited to the theoretical understanding of turbulence, but they carry over to the modelling of turbulent flows. For example, stochastic models for the velocity gradient should in principle obey the constraints (1.1) and (1.2) (Johnson & Meneveau Reference Johnson and Meneveau2016), which help to reduce the number of free parameters in such models (Leppin & Wilczek Reference Leppin and Wilczek2020). The homogeneity relations can also be used to improve the performance of neural networks designed for machine learning of turbulent flows by including them into the training (Tian, Livescu & Chertkov Reference Tian, Livescu and Chertkov2021; Momenifar et al. Reference Momenifar, Diao, Tarokh and Bragg2022).
The Betchov relations (1.1) and (1.2) follow by writing the matrix traces ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}}^2)$ and
$\textrm {Tr}(\boldsymbol{\mathsf{A}}^2)$ and ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}}^3)$ as the divergence of a vector field. Then, because of statistical homogeneity, the average of such traces is zero since a spatial derivative can be factored out, and it acts on an average that does not depend on space explicitly. For example, due to incompressibility, the second principal invariant of the velocity gradient can be rewritten as
$\textrm {Tr}(\boldsymbol{\mathsf{A}}^3)$ as the divergence of a vector field. Then, because of statistical homogeneity, the average of such traces is zero since a spatial derivative can be factored out, and it acts on an average that does not depend on space explicitly. For example, due to incompressibility, the second principal invariant of the velocity gradient can be rewritten as
so that its average vanishes, and relation (1.1) follows. An analogous procedure applies to retrieve (1.2), since the third principal invariant can be expressed as
However, while it is straightforward to check the validity of the Betchov homogeneity relations for the velocity gradient, it is more complicated to show whether those homogeneity relations are the only possible ones or if additional constraints exist. If there existed higher-order constraints, we could, for example, improve the current reduced-order models of the velocity gradient dynamics just by imposing these additional homogeneity constraints.
Most of the previous attempts to find higher-order homogeneity relations were based on swapping the spatial derivatives: a scalar contraction of powers of the velocity gradient is manipulated by factoring out the spatial derivative, in order to rewrite the contraction as the divergence of some quantity (if possible). Attempts to obtain relations for the fourth-order moments of the velocity increments/gradients through this derivative-swapping procedure include Hill (Reference Hill1997), Hierro & Dopazo (Reference Hierro and Dopazo2003) and Bragg et al. (Reference Bragg, Hammond, Dhariwal and Meng2022). However, it is very difficult to show the completeness of the homogeneity constraints for the velocity gradient through this approach. One would need to consider linear combinations of infinitely many contractions of the velocity gradients and try to recast them into the spatial derivative of some field. In this framework, Siggia (Reference Siggia1981) showed that no homogeneity constraints exist on polynomials of fourth-order velocity gradient invariants.
Interestingly, the scenario is analogous to the search for inviscid invariants of the Navier–Stokes equations (Majda & Bertozzi Reference Majda and Bertozzi2001), which are central for the occurrence of cascades (Alexakis & Biferale Reference Alexakis and Biferale2018). While it is straightforward to check the conservation of kinetic energy and helicity in the incompressible three-dimensional Euler equations by a derivative-swapping procedure (Majda & Bertozzi Reference Majda and Bertozzi2001), it is much more involved to show whether those conserved quantities are the only possible ones or if additional ones exist. This completeness question has been answered by Serre (Reference Serre1984) for the incompressible Euler equations and by Enciso, Peralta-Salas & de Lizaur (Reference Enciso, Peralta-Salas and de Lizaur2016) for volume-preserving diffeomorphisms.
In this work, we investigate the existence of higher-order homogeneity constraints for the velocity gradient using tensor function representation theory (Zheng Reference Zheng1994; Itskov Reference Itskov2015). The analysis allows one to identify the homogeneity relations as the solutions of a system of partial differential equations, and it shows that no additional homogeneity constraints for the incompressible velocity gradient exist other than those already known from Betchov (Reference Betchov1956). We furthermore extend the analysis to the velocity gradients as perceived by Lagrangian tetrads in turbulence (Chertkov et al. Reference Chertkov, Pumir and Shraiman1999; Naso & Pumir Reference Naso and Pumir2005; Xu et al. Reference Xu, Pumir and Bodenschatz2011); in particular, we show the completeness of the homogeneity relations for compressible/perceived gradients derived in Yang et al. (Reference Yang, Pumir and Xu2020, Reference Yang, Fang, Fang, Pumir and Xu2022).
2. An equation encoding the homogeneity constraints on the velocity gradient
We consider a three-dimensional, incompressible and statistically homogeneous and isotropic velocity field ![]() $\boldsymbol {u}(\boldsymbol {x},t)$, together with its spatial gradient
$\boldsymbol {u}(\boldsymbol {x},t)$, together with its spatial gradient ![]() $\boldsymbol{\mathsf{A}}=\boldsymbol {\nabla } \boldsymbol {u}$ (
$\boldsymbol{\mathsf{A}}=\boldsymbol {\nabla } \boldsymbol {u}$ (![]() $A_{ij}=\boldsymbol {\nabla }_j \,u_i$ in Cartesian component notation). Incompressibility implies that
$A_{ij}=\boldsymbol {\nabla }_j \,u_i$ in Cartesian component notation). Incompressibility implies that ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}})=0$; we will extend the analysis to the compressible case afterwards.
$\textrm {Tr}(\boldsymbol{\mathsf{A}})=0$; we will extend the analysis to the compressible case afterwards.
We search for homogeneity relations for scalar single-point statistics of the velocity gradient only. By ‘homogeneity constraint’ we mean the vanishing of an average of a scalar quantity due to homogeneity. Statistical homogeneity means that all statistical quantities are invariant under spatial translations. In particular, single-point statistics do not explicitly depend on the spatial coordinate. As a consequence, any scalar field ![]() $\phi$ that is the divergence of a vector field,
$\phi$ that is the divergence of a vector field, ![]() $\phi =\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {F}$, has zero ensemble/spatial average:
$\phi =\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {F}$, has zero ensemble/spatial average:
For example, in the first Betchov relation ![]() $\langle \mathrm {Tr}(\boldsymbol{\mathsf{A}}^2) \rangle =0$, the vector field is
$\langle \mathrm {Tr}(\boldsymbol{\mathsf{A}}^2) \rangle =0$, the vector field is ![]() $\boldsymbol {F}=\boldsymbol{\mathsf{A}}\boldsymbol {u}$ (
$\boldsymbol {F}=\boldsymbol{\mathsf{A}}\boldsymbol {u}$ (![]() $F_i=A_{ij}u_j$ in component notation, see (1.3)). To generalize this, we search for scalar functions of the velocity gradient
$F_i=A_{ij}u_j$ in component notation, see (1.3)). To generalize this, we search for scalar functions of the velocity gradient ![]() $\phi (\boldsymbol{\mathsf{A}})$ that are the divergence of a vector field
$\phi (\boldsymbol{\mathsf{A}})$ that are the divergence of a vector field ![]() $\boldsymbol {F}$.
$\boldsymbol {F}$.
The vector field ![]() $\boldsymbol {F}$ is in general a functional of the velocity field
$\boldsymbol {F}$ is in general a functional of the velocity field ![]() $\boldsymbol {u}(\boldsymbol {x},t)$. We restrict the analysis to functions of the velocity and its spatial derivatives because we search for homogeneity relations on the single-point statistics of the velocity gradient. By restricting the analysis to functions of the velocity and its spatial derivatives, we are implicitly assuming isotropy. Indeed, in a statistically isotropic flow, the governing equations and associated boundary conditions do not introduce any characteristic direction. Therefore, in that statistically isotropic situation, the velocity and velocity gradients are all the possible variables upon which the vector
$\boldsymbol {u}(\boldsymbol {x},t)$. We restrict the analysis to functions of the velocity and its spatial derivatives because we search for homogeneity relations on the single-point statistics of the velocity gradient. By restricting the analysis to functions of the velocity and its spatial derivatives, we are implicitly assuming isotropy. Indeed, in a statistically isotropic flow, the governing equations and associated boundary conditions do not introduce any characteristic direction. Therefore, in that statistically isotropic situation, the velocity and velocity gradients are all the possible variables upon which the vector ![]() $\boldsymbol {F}$ can depend. We thereby exclude, for example, rotations of the frame of the flow, anisotropic forcing, boundary layers, etc.
$\boldsymbol {F}$ can depend. We thereby exclude, for example, rotations of the frame of the flow, anisotropic forcing, boundary layers, etc.
Focusing on single-point statistics of isotropic flows, we have ![]() $\boldsymbol {F} = \boldsymbol {F}(\boldsymbol {u}, \boldsymbol{\mathsf{A}}, \boldsymbol {\nabla }\boldsymbol{\mathsf{A}}, \boldsymbol {\nabla } (\boldsymbol {\nabla } \boldsymbol{\mathsf{A}}), \ldots )$ so that the corresponding
$\boldsymbol {F} = \boldsymbol {F}(\boldsymbol {u}, \boldsymbol{\mathsf{A}}, \boldsymbol {\nabla }\boldsymbol{\mathsf{A}}, \boldsymbol {\nabla } (\boldsymbol {\nabla } \boldsymbol{\mathsf{A}}), \ldots )$ so that the corresponding ![]() $\phi (\boldsymbol{\mathsf{A}})$ is, by the chain rule and in component notation,
$\phi (\boldsymbol{\mathsf{A}})$ is, by the chain rule and in component notation,
The fact that the left-hand side of (2.2) depends only on the velocity gradient strongly constrains the functional form of the vector field ![]() $\boldsymbol {F}$. Namely, the right-hand side of (2.2) should explicitly involve neither the velocity
$\boldsymbol {F}$. Namely, the right-hand side of (2.2) should explicitly involve neither the velocity ![]() $\boldsymbol {u}$ nor the gradients of the velocity gradient,
$\boldsymbol {u}$ nor the gradients of the velocity gradient, ![]() $\boldsymbol {\nabla } \boldsymbol{\mathsf{A}}$,
$\boldsymbol {\nabla } \boldsymbol{\mathsf{A}}$, ![]() $\boldsymbol {\nabla } (\boldsymbol {\nabla } \boldsymbol{\mathsf{A}})$, etc. This implies that all the terms on the right-hand side of (2.2) featuring gradients of the velocity gradient should identically cancel, while only
$\boldsymbol {\nabla } (\boldsymbol {\nabla } \boldsymbol{\mathsf{A}})$, etc. This implies that all the terms on the right-hand side of (2.2) featuring gradients of the velocity gradient should identically cancel, while only ![]() $(\partial F_i/\partial u_{p}) A_{pi}$ can contribute to
$(\partial F_i/\partial u_{p}) A_{pi}$ can contribute to ![]() $\phi$. Moreover, the part of
$\phi$. Moreover, the part of ![]() $(\partial F_i/\partial u_{p}) A_{pi}$ that contributes to
$(\partial F_i/\partial u_{p}) A_{pi}$ that contributes to ![]() $\phi$ can depend only on
$\phi$ can depend only on ![]() $\boldsymbol{\mathsf{A}}$.
$\boldsymbol{\mathsf{A}}$.
Therefore, we just need to consider vector functions of the velocity and velocity gradient, ![]() $\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$, that are linear in the velocity. Based on this, (2.2) splits into
$\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$, that are linear in the velocity. Based on this, (2.2) splits into
Equation (2.3b) yields the main differential equation to determine ![]() $\boldsymbol {F}$. The gradient of the gradient,
$\boldsymbol {F}$. The gradient of the gradient, ![]() $\boldsymbol {\nabla }_i\,A_{pq}=\boldsymbol {\nabla }_i\boldsymbol {\nabla }_q \,u_p$, is symmetric in
$\boldsymbol {\nabla }_i\,A_{pq}=\boldsymbol {\nabla }_i\boldsymbol {\nabla }_q \,u_p$, is symmetric in ![]() $i$ and
$i$ and ![]() $q$, so that only the part of
$q$, so that only the part of ![]() $\partial F_i/\partial A_{pq}$ that is symmetric in
$\partial F_i/\partial A_{pq}$ that is symmetric in ![]() $i$ and
$i$ and ![]() $q$ contributes to (2.3b). Additionally, the contractions
$q$ contributes to (2.3b). Additionally, the contractions ![]() $i,p$ and
$i,p$ and ![]() $q,p$ of
$q,p$ of ![]() $\boldsymbol {\nabla }_i\,A_{pq}$ are zero by incompressibility. Therefore,
$\boldsymbol {\nabla }_i\,A_{pq}$ are zero by incompressibility. Therefore, ![]() $\boldsymbol {F}$ solves (2.3b) only if, for some vector
$\boldsymbol {F}$ solves (2.3b) only if, for some vector ![]() $\boldsymbol {v}$,
$\boldsymbol {v}$,
Here, ![]() $\delta _{ij}$ denotes the Kronecker delta, and the vector
$\delta _{ij}$ denotes the Kronecker delta, and the vector ![]() $\boldsymbol {v}$ is easily determined by contracting two of the free indices, e.g.
$\boldsymbol {v}$ is easily determined by contracting two of the free indices, e.g. ![]() $v_p=\partial F_{k}/\partial A_{pk}$.
$v_p=\partial F_{k}/\partial A_{pk}$.
Equations (2.3) and (2.4) allow the search for homogeneity constraints to be more systematic: instead of attempting to factor out the spatial derivatives in tensor contractions of velocity gradients, we need to solve a system of partial differential equations. Solving (2.4) for vectors ![]() $\boldsymbol {F}$ that are linear in
$\boldsymbol {F}$ that are linear in ![]() $\boldsymbol {u}$ yields all possible vectors
$\boldsymbol {u}$ yields all possible vectors ![]() $\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$, whose divergence depends only on the velocity gradient,
$\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$, whose divergence depends only on the velocity gradient, ![]() $\phi (\boldsymbol{\mathsf{A}}) = \boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$, as in (2.3a). Therefore, finding all solutions of (2.4) that are linear in the velocity amounts to deriving all possible homogeneity constraints on scalar functions of an incompressible and statistically isotropic velocity gradient.
$\phi (\boldsymbol{\mathsf{A}}) = \boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$, as in (2.3a). Therefore, finding all solutions of (2.4) that are linear in the velocity amounts to deriving all possible homogeneity constraints on scalar functions of an incompressible and statistically isotropic velocity gradient.
3. Tensor function representation of the homogeneity constraints
In the following, we construct the general isotropic tensor function ![]() $\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$. Tensor function representation theory (Weyl Reference Weyl1946; Rivlin & Ericksen Reference Rivlin and Ericksen1955; Pennisi & Trovato Reference Pennisi and Trovato1987; Zheng Reference Zheng1994; Itskov Reference Itskov2015) allows one to write down all possible vector functions
$\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$. Tensor function representation theory (Weyl Reference Weyl1946; Rivlin & Ericksen Reference Rivlin and Ericksen1955; Pennisi & Trovato Reference Pennisi and Trovato1987; Zheng Reference Zheng1994; Itskov Reference Itskov2015) allows one to write down all possible vector functions ![]() $\boldsymbol {F}$ of the generating vector
$\boldsymbol {F}$ of the generating vector ![]() $\boldsymbol {u}$ and tensor
$\boldsymbol {u}$ and tensor ![]() $\boldsymbol{\mathsf{A}}$ that transform consistently under any change of basis: when the arguments
$\boldsymbol{\mathsf{A}}$ that transform consistently under any change of basis: when the arguments ![]() $\boldsymbol {u}$ and
$\boldsymbol {u}$ and ![]() $\boldsymbol{\mathsf{A}}$ undergo a rotation,
$\boldsymbol{\mathsf{A}}$ undergo a rotation, ![]() $\boldsymbol {F}$ rotates accordingly (Itskov Reference Itskov2015). The vector field
$\boldsymbol {F}$ rotates accordingly (Itskov Reference Itskov2015). The vector field ![]() $\boldsymbol {F}$ will be finally determined by requiring that it is linear in
$\boldsymbol {F}$ will be finally determined by requiring that it is linear in ![]() $\boldsymbol {u}$ and that it solves (2.4).
$\boldsymbol {u}$ and that it solves (2.4).
In general, ![]() $\boldsymbol {F}$ can depend separately on the symmetric and antisymmetric parts of the velocity gradient (Rivlin & Ericksen Reference Rivlin and Ericksen1955):
$\boldsymbol {F}$ can depend separately on the symmetric and antisymmetric parts of the velocity gradient (Rivlin & Ericksen Reference Rivlin and Ericksen1955):
with ![]() $\boldsymbol{\mathsf{A}}^{\rm T}$ denoting the matrix transpose of
$\boldsymbol{\mathsf{A}}^{\rm T}$ denoting the matrix transpose of ![]() $\boldsymbol{\mathsf{A}}$. Therefore, we consider all the vector functions
$\boldsymbol{\mathsf{A}}$. Therefore, we consider all the vector functions ![]() $\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{S}},\boldsymbol{\mathsf{W}})$ constructed through the velocity and velocity gradients that, due to (2.3a), are linear in the velocity:
$\boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{S}},\boldsymbol{\mathsf{W}})$ constructed through the velocity and velocity gradients that, due to (2.3a), are linear in the velocity:
 \begin{equation} \boldsymbol{F} = \sum_{n=0}^{8} \,f_{n} (\mathcal{I}) \boldsymbol{\mathsf{B}}^n \boldsymbol{u}. \end{equation}
\begin{equation} \boldsymbol{F} = \sum_{n=0}^{8} \,f_{n} (\mathcal{I}) \boldsymbol{\mathsf{B}}^n \boldsymbol{u}. \end{equation}
Here ![]() $\boldsymbol{\mathsf{B}}^n$ are the basis tensors that can be formed through
$\boldsymbol{\mathsf{B}}^n$ are the basis tensors that can be formed through ![]() $\boldsymbol{\mathsf{S}}$ and
$\boldsymbol{\mathsf{S}}$ and ![]() $\boldsymbol{\mathsf{W}}$ (Pennisi & Trovato Reference Pennisi and Trovato1987):
$\boldsymbol{\mathsf{W}}$ (Pennisi & Trovato Reference Pennisi and Trovato1987):
 \begin{equation} \left.\begin{gathered} \begin{aligned}[c] \boldsymbol{\mathsf{B}}^0 & = \boldsymbol{\mathsf{I}}, \\ \boldsymbol{\mathsf{B}}^1 & = \boldsymbol{\mathsf{S}}, \\ \boldsymbol{\mathsf{B}}^2 & = \boldsymbol{\mathsf{W}}, \end{aligned}\quad \begin{aligned}[c] \boldsymbol{\mathsf{B}}^3 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{S}},\\ \boldsymbol{\mathsf{B}}^4 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} - \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}},\\ \boldsymbol{\mathsf{B}}^5 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} + \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}}, \end{aligned}\quad \begin{aligned}[c] \boldsymbol{\mathsf{B}}^6 & = \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{W}}, \\ \boldsymbol{\mathsf{B}}^7 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{W}} + \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}}, \\ \boldsymbol{\mathsf{B}}^8 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} + \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{S}}, \end{aligned} \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \begin{aligned}[c] \boldsymbol{\mathsf{B}}^0 & = \boldsymbol{\mathsf{I}}, \\ \boldsymbol{\mathsf{B}}^1 & = \boldsymbol{\mathsf{S}}, \\ \boldsymbol{\mathsf{B}}^2 & = \boldsymbol{\mathsf{W}}, \end{aligned}\quad \begin{aligned}[c] \boldsymbol{\mathsf{B}}^3 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{S}},\\ \boldsymbol{\mathsf{B}}^4 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} - \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}},\\ \boldsymbol{\mathsf{B}}^5 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} + \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}}, \end{aligned}\quad \begin{aligned}[c] \boldsymbol{\mathsf{B}}^6 & = \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{W}}, \\ \boldsymbol{\mathsf{B}}^7 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{W}} + \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}}, \\ \boldsymbol{\mathsf{B}}^8 & = \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}} + \boldsymbol{\mathsf{W}} \boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{S}}, \end{aligned} \end{gathered}\right\} \end{equation}
with ![]() $\boldsymbol{\mathsf{I}}$ denoting the identity matrix and the standard matrix product is implied. Two additional tensors would be necessary to fix degeneracies of the basis (3.3), which occur when the vorticity is an eigenvector of the strain-rate tensor or the strain rate has two identical eigenvalues (Rivlin & Ericksen Reference Rivlin and Ericksen1955). We ignore that zero-measure configuration of the gradients. Also, note that the superscript of
$\boldsymbol{\mathsf{I}}$ denoting the identity matrix and the standard matrix product is implied. Two additional tensors would be necessary to fix degeneracies of the basis (3.3), which occur when the vorticity is an eigenvector of the strain-rate tensor or the strain rate has two identical eigenvalues (Rivlin & Ericksen Reference Rivlin and Ericksen1955). We ignore that zero-measure configuration of the gradients. Also, note that the superscript of ![]() $\boldsymbol{\mathsf{B}}^n$ serves to number the basis tensors rather than indicating powers of the tensor.
$\boldsymbol{\mathsf{B}}^n$ serves to number the basis tensors rather than indicating powers of the tensor.
The components ![]() $f_n$ in (3.2) are functions of the set
$f_n$ in (3.2) are functions of the set ![]() $\mathcal {I}$ of independent invariants that can be formed through the velocity gradients (Pennisi & Trovato Reference Pennisi and Trovato1987):
$\mathcal {I}$ of independent invariants that can be formed through the velocity gradients (Pennisi & Trovato Reference Pennisi and Trovato1987):
 \begin{align} \left.\begin{aligned}
\mathcal{I}_1 &=
\textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}}), \quad\ \ \, \mathcal{I}_3
= \textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}}), \quad \mathcal{I}_5
= \textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}}
\boldsymbol{\mathsf{W}}), \\ \mathcal{I}_2 &=
\textrm{Tr}(\boldsymbol{\mathsf{W}}
\boldsymbol{\mathsf{W}}), \quad \mathcal{I}_4
= \textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{W}}
\boldsymbol{\mathsf{W}}),\end{aligned}\right\}
\end{align}
\begin{align} \left.\begin{aligned}
\mathcal{I}_1 &=
\textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}}), \quad\ \ \, \mathcal{I}_3
= \textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}}), \quad \mathcal{I}_5
= \textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{S}} \boldsymbol{\mathsf{W}}
\boldsymbol{\mathsf{W}}), \\ \mathcal{I}_2 &=
\textrm{Tr}(\boldsymbol{\mathsf{W}}
\boldsymbol{\mathsf{W}}), \quad \mathcal{I}_4
= \textrm{Tr}(\boldsymbol{\mathsf{S}}
\boldsymbol{\mathsf{W}}
\boldsymbol{\mathsf{W}}),\end{aligned}\right\}
\end{align}
with standard matrix product implied. A sixth invariant would be necessary to fix the orientation/handedness of the vorticity with respect to the strain-rate eigenvectors. We do not consider the sixth invariant as an independent variable, since it is determined by the invariants (3.4) up to a sign (Lund & Novikov Reference Lund and Novikov1992).
The number of basis tensors and independent invariants is finite due to the Cayley–Hamilton theorem, which plays a major role in the theory of tensor representation (Rivlin & Ericksen Reference Rivlin and Ericksen1955). Betchov (Reference Betchov1956) showed that the average of the velocity gradient principal invariants is zero in a homogeneous flow, thus constraining all the independent traces of powers of ![]() $\boldsymbol{\mathsf{A}}$. However, one can take contractions of combinations of the strain rate and rotation rate, and pose the question whether the average of those scalar contractions vanishes due to homogeneity.
$\boldsymbol{\mathsf{A}}$. However, one can take contractions of combinations of the strain rate and rotation rate, and pose the question whether the average of those scalar contractions vanishes due to homogeneity.
4. Solution of the equation encoding the homogeneity constraints
We use the general expression (3.2) combined with (2.4) in order to determine the components ![]() $f_n(\mathcal {I})$ of
$f_n(\mathcal {I})$ of ![]() $\boldsymbol {F}$. This will yield a vector field
$\boldsymbol {F}$. This will yield a vector field ![]() $\boldsymbol {F}$ associated with the homogeneity constraints for the velocity gradient through
$\boldsymbol {F}$ associated with the homogeneity constraints for the velocity gradient through ![]() $\phi (\boldsymbol{\mathsf{A}}) = \boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$ and (2.1).
$\phi (\boldsymbol{\mathsf{A}}) = \boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {F}(\boldsymbol {u},\boldsymbol{\mathsf{A}})$ and (2.1).
Inserting the general expression (3.2) of ![]() $\boldsymbol {F}$ into (2.4) gives, in component notation,
$\boldsymbol {F}$ into (2.4) gives, in component notation,
 \begin{equation} \left[\frac{\partial f_l}{\partial \mathcal{I}_k} \frac{\partial \mathcal{I}_k}{\partial A_{pq}} B^l_{ij} + \frac{\partial f_l}{\partial \mathcal{I}_k} \frac{\partial \mathcal{I}_k}{\partial A_{pi}} B^l_{qj} + f_l \frac{\partial B^l_{ij}}{\partial A_{pq}} + f_l \frac{\partial B^l_{qj}}{\partial A_{pi}}\right]u_j = v_i\delta_{pq} + v_q\delta_{pi}. \end{equation}
\begin{equation} \left[\frac{\partial f_l}{\partial \mathcal{I}_k} \frac{\partial \mathcal{I}_k}{\partial A_{pq}} B^l_{ij} + \frac{\partial f_l}{\partial \mathcal{I}_k} \frac{\partial \mathcal{I}_k}{\partial A_{pi}} B^l_{qj} + f_l \frac{\partial B^l_{ij}}{\partial A_{pq}} + f_l \frac{\partial B^l_{qj}}{\partial A_{pi}}\right]u_j = v_i\delta_{pq} + v_q\delta_{pi}. \end{equation}Here and throughout, repeated indices imply summation, unless otherwise specified. As shown in Appendix A, the derivatives of the invariants (3.4) can be written as
while the derivatives of the basis tensors (3.3) can be expressed as
with ![]() $0\le l,m,n\le 8$ and
$0\le l,m,n\le 8$ and ![]() $1\le k\le 5$.
$1\le k\le 5$.
The matrix entries ![]() $M_{km}$ featured in (4.2) are specified in (A1). The symbols
$M_{km}$ featured in (4.2) are specified in (A1). The symbols ![]() $\varGamma ^{P,n}_{lm}$ in (4.3) play the role of Christoffel symbols (Grinfeld Reference Grinfeld2013) and their components are listed in (A9), (A10) and (A11). Inserting the expressions (4.2) and (4.3) for the derivatives into (4.1) yields the following independent equations:
$\varGamma ^{P,n}_{lm}$ in (4.3) play the role of Christoffel symbols (Grinfeld Reference Grinfeld2013) and their components are listed in (A9), (A10) and (A11). Inserting the expressions (4.2) and (4.3) for the derivatives into (4.1) yields the following independent equations:
Equations (4.4) should hold for all ![]() $\boldsymbol {u}$ and
$\boldsymbol {u}$ and ![]() $\boldsymbol{\mathsf{A}}$, so that, separating out the basis tensors, we have the following equations for the components:
$\boldsymbol{\mathsf{A}}$, so that, separating out the basis tensors, we have the following equations for the components:
 $$\begin{gather} \sum_{n=0}^8 [ \varGamma^{2,n}_{lm} + t(l)\varGamma^{2,n}_{lm} ] f_n = 0, \quad \forall\ 0\le l, m \le 8, \end{gather}$$
$$\begin{gather} \sum_{n=0}^8 [ \varGamma^{2,n}_{lm} + t(l)\varGamma^{2,n}_{lm} ] f_n = 0, \quad \forall\ 0\le l, m \le 8, \end{gather}$$ $$\begin{gather}\sum_{k=1}^5 \frac{\partial f_l}{\partial\mathcal{I}_k}M_{km} ={-}\sum_{n=0}^8 [\varGamma^{3,n}_{lm} + t(m)\varGamma^{1,n}_{ml}]f_n, \quad \forall\ 0\le l \le 8, 1\le m \le 8, \end{gather}$$
$$\begin{gather}\sum_{k=1}^5 \frac{\partial f_l}{\partial\mathcal{I}_k}M_{km} ={-}\sum_{n=0}^8 [\varGamma^{3,n}_{lm} + t(m)\varGamma^{1,n}_{ml}]f_n, \quad \forall\ 0\le l \le 8, 1\le m \le 8, \end{gather}$$
where indices ![]() $l,m$ are not contracted, and
$l,m$ are not contracted, and ![]() $t(l)=1$ if
$t(l)=1$ if ![]() $\boldsymbol{\mathsf{B}}^l$ is symmetric and
$\boldsymbol{\mathsf{B}}^l$ is symmetric and ![]() $t(l)=-1$ if
$t(l)=-1$ if ![]() $\boldsymbol{\mathsf{B}}^l$ is antisymmetric. In the steps from (4.4b) to (4.5b), the components at
$\boldsymbol{\mathsf{B}}^l$ is antisymmetric. In the steps from (4.4b) to (4.5b), the components at ![]() $m=0$ have been absorbed into the generic right-hand side
$m=0$ have been absorbed into the generic right-hand side ![]() $v_i B^0_{pq}$ of (4.4b), and therefore (4.5b) only concerns components with
$v_i B^0_{pq}$ of (4.4b), and therefore (4.5b) only concerns components with ![]() $m\ge 1$.
$m\ge 1$.
The linear system (4.5a) of 81 equations in the nine variables ![]() $f_n$,
$f_n$, ![]() $0\le n\le 8$, can be solved using symbolic calculus (Meurer et al. Reference Meurer2017). This yields
$0\le n\le 8$, can be solved using symbolic calculus (Meurer et al. Reference Meurer2017). This yields
Next, (4.5b) has a solution only if, for all ![]() $l$, the right-hand side is orthogonal to the kernel of
$l$, the right-hand side is orthogonal to the kernel of ![]() $\boldsymbol{\mathsf{M}}$, but this condition imposes no further constraints on
$\boldsymbol{\mathsf{M}}$, but this condition imposes no further constraints on ![]() $f_n$. Finally, with this orthogonality condition ensured, the derivatives
$f_n$. Finally, with this orthogonality condition ensured, the derivatives ![]() $\partial f_l/\partial \mathcal {I}_k$ are obtained by multiplying (4.5b) by the Moore–Penrose inverse of
$\partial f_l/\partial \mathcal {I}_k$ are obtained by multiplying (4.5b) by the Moore–Penrose inverse of ![]() $\boldsymbol{\mathsf{M}}$, with components
$\boldsymbol{\mathsf{M}}$, with components ![]() $M^{-1}_{mk'}$, thus yielding
$M^{-1}_{mk'}$, thus yielding
By solving the straightforward linear system (4.7) with the conditions (4.6a–c), we obtain the components ![]() $f_n$ of
$f_n$ of ![]() $\boldsymbol {F}$ that solves (2.4) and is linear in
$\boldsymbol {F}$ that solves (2.4) and is linear in ![]() $\boldsymbol {u}$:
$\boldsymbol {u}$:
where the ![]() $\bar {f}_n$ are arbitrary constants. The solution (4.8) of (2.4) encodes all the Betchov constraints, since its divergence yields the gradient principal invariants
$\bar {f}_n$ are arbitrary constants. The solution (4.8) of (2.4) encodes all the Betchov constraints, since its divergence yields the gradient principal invariants
thus retrieving (1.3) and (1.4) and, by homogeneity, ![]() $\langle \,\bar {f}_2\,\textrm {Tr}(\boldsymbol{\mathsf{A}}^2) + \bar {f}_3\,\textrm {Tr}(\boldsymbol{\mathsf{A}}^3) \rangle =0$.
$\langle \,\bar {f}_2\,\textrm {Tr}(\boldsymbol{\mathsf{A}}^2) + \bar {f}_3\,\textrm {Tr}(\boldsymbol{\mathsf{A}}^3) \rangle =0$.
The Betchov homogeneity relations, obtained by averaging (4.9), are all the possible homogeneity constraints on the single-point statistics of an incompressible and isotropic gradient since they follow from all the independent solutions of (2.4). In other words, no scalar function of the velocity gradient invariants can be written as the divergence of a vector field, other than the principal invariants ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}}^2)=\mathcal {I}_1+\mathcal {I}_2$ and
$\textrm {Tr}(\boldsymbol{\mathsf{A}}^2)=\mathcal {I}_1+\mathcal {I}_2$ and ![]() $\textrm {Tr}(\boldsymbol{\mathsf{A}}^3)=\mathcal {I}_3+3\mathcal {I}_4$.
$\textrm {Tr}(\boldsymbol{\mathsf{A}}^3)=\mathcal {I}_3+3\mathcal {I}_4$.
5. Homogeneity constraints for the velocity gradient and additional quantities
Equation (4.8) shows that the homogeneity relations for the velocity gradient alone consist only of the two Betchov constraints. However, generalizations of (4.8) easily generate homogeneity constraints concerning the velocity gradient together with additional variables. Indeed, the divergence of ![]() $\boldsymbol {F}$ in (4.8) does not depend on the gradient of the velocity gradient even when
$\boldsymbol {F}$ in (4.8) does not depend on the gradient of the velocity gradient even when ![]() $\boldsymbol {u}$ in (4.8) is replaced by any scalar, vector or tensor quantity
$\boldsymbol {u}$ in (4.8) is replaced by any scalar, vector or tensor quantity ![]() $\boldsymbol{\mathsf{q}}$ that does not explicitly depend on the velocity gradient itself. This is because
$\boldsymbol{\mathsf{q}}$ that does not explicitly depend on the velocity gradient itself. This is because ![]() $\boldsymbol {F}$ solves (2.4), which features only derivatives with respect to
$\boldsymbol {F}$ solves (2.4), which features only derivatives with respect to ![]() $\boldsymbol{\mathsf{A}}$, while the dependence of
$\boldsymbol{\mathsf{A}}$, while the dependence of ![]() $\boldsymbol {F}$ upon
$\boldsymbol {F}$ upon ![]() $\boldsymbol {u}$ is parametric. Therefore, for any vector
$\boldsymbol {u}$ is parametric. Therefore, for any vector ![]() $\boldsymbol {q}$, one can construct homogeneity relations for the scalar quantities
$\boldsymbol {q}$, one can construct homogeneity relations for the scalar quantities
where the standard matrix–vector product is implied and the left-hand side depends neither on ![]() $\boldsymbol {q}$ nor on
$\boldsymbol {q}$ nor on ![]() $\boldsymbol {\nabla }\boldsymbol{\mathsf{A}}$. For example, using (5.1) with the pressure gradient divided by the fluid density,
$\boldsymbol {\nabla }\boldsymbol{\mathsf{A}}$. For example, using (5.1) with the pressure gradient divided by the fluid density, ![]() $\boldsymbol {q}=\boldsymbol {\nabla } P/\rho$, yields homogeneity relations for the pressure Hessian in incompressible flows, namely
$\boldsymbol {q}=\boldsymbol {\nabla } P/\rho$, yields homogeneity relations for the pressure Hessian in incompressible flows, namely ![]() $\langle A_{ij} \boldsymbol {\nabla }_i\boldsymbol {\nabla }_j \,P \rangle =0$ and
$\langle A_{ij} \boldsymbol {\nabla }_i\boldsymbol {\nabla }_j \,P \rangle =0$ and ![]() $\langle A_{ik}A_{kj}\boldsymbol {\nabla }_i\boldsymbol {\nabla }_j\,P \rangle = -\rho \langle (A_{ij}A_{ji})^2 \rangle /2$. Analogously, employing (5.1) with the velocity Laplacian,
$\langle A_{ik}A_{kj}\boldsymbol {\nabla }_i\boldsymbol {\nabla }_j\,P \rangle = -\rho \langle (A_{ij}A_{ji})^2 \rangle /2$. Analogously, employing (5.1) with the velocity Laplacian, ![]() $\boldsymbol {q}=\nabla ^2 \boldsymbol {u}$, gives homogeneity relations for the Laplacian of a traceless gradient,
$\boldsymbol {q}=\nabla ^2 \boldsymbol {u}$, gives homogeneity relations for the Laplacian of a traceless gradient, ![]() $\langle A_{ij} \nabla ^2 A_{ji} \rangle =0$ and
$\langle A_{ij} \nabla ^2 A_{ji} \rangle =0$ and ![]() $\langle A_{ik}A_{kj}\nabla ^2 A_{ji} \rangle =0$. Such relations play an important role in the budget equation for the turbulent dissipation rate (Buaria, Pumir & Bodenschatz Reference Buaria, Pumir and Bodenschatz2022), and turn out to be useful in the Lagrangian modelling of velocity gradients (Leppin & Wilczek Reference Leppin and Wilczek2020).
$\langle A_{ik}A_{kj}\nabla ^2 A_{ji} \rangle =0$. Such relations play an important role in the budget equation for the turbulent dissipation rate (Buaria, Pumir & Bodenschatz Reference Buaria, Pumir and Bodenschatz2022), and turn out to be useful in the Lagrangian modelling of velocity gradients (Leppin & Wilczek Reference Leppin and Wilczek2020).
6. Homogeneity constraints for compressible and perceived velocity gradients
The analysis presented in the previous sections easily generalizes, e.g. to compressible or two-dimensional flows. In this section we consider a compressible velocity gradient ![]() $\tilde {\boldsymbol{\mathsf{A}}}$, with non-zero trace
$\tilde {\boldsymbol{\mathsf{A}}}$, with non-zero trace ![]() $\widetilde {\mathcal {I}}_0=\textrm {Tr}(\tilde {\boldsymbol{\mathsf{A}}})$ (the tilde denoting quantities relative to the compressible velocity field). The presented homogeneity analysis allows one to prove the completeness of the homogeneity constraints recently derived in Yang et al. (Reference Yang, Pumir and Xu2020) for a compressible gradient, which hold approximately even in strongly non-homogeneous compressible turbulence (Yang et al. Reference Yang, Fang, Fang, Pumir and Xu2022). Additionally, they apply one-to-one to the perceived velocity gradient (or tetrad) dynamics in homogeneous flows (Chertkov et al. Reference Chertkov, Pumir and Shraiman1999; Xu et al. Reference Xu, Pumir and Bodenschatz2011).
$\widetilde {\mathcal {I}}_0=\textrm {Tr}(\tilde {\boldsymbol{\mathsf{A}}})$ (the tilde denoting quantities relative to the compressible velocity field). The presented homogeneity analysis allows one to prove the completeness of the homogeneity constraints recently derived in Yang et al. (Reference Yang, Pumir and Xu2020) for a compressible gradient, which hold approximately even in strongly non-homogeneous compressible turbulence (Yang et al. Reference Yang, Fang, Fang, Pumir and Xu2022). Additionally, they apply one-to-one to the perceived velocity gradient (or tetrad) dynamics in homogeneous flows (Chertkov et al. Reference Chertkov, Pumir and Shraiman1999; Xu et al. Reference Xu, Pumir and Bodenschatz2011).
As done above for the incompressible gradient, we search for a scalar function of the compressible gradient only, ![]() $\tilde {\phi }(\tilde {\boldsymbol{\mathsf{A}}})$, that has zero average due to statistical homogeneity. In the compressible case, the components
$\tilde {\phi }(\tilde {\boldsymbol{\mathsf{A}}})$, that has zero average due to statistical homogeneity. In the compressible case, the components ![]() $\tilde {f}_n$ of the vector field
$\tilde {f}_n$ of the vector field ![]() $\tilde {\boldsymbol {F}}$ associated with the homogeneity constraints through
$\tilde {\boldsymbol {F}}$ associated with the homogeneity constraints through ![]() $\tilde {\phi }(\tilde {\boldsymbol{\mathsf{A}}}) = \boldsymbol {\nabla }\boldsymbol {\cdot }\tilde {\boldsymbol {F}}$ depend on the additional invariant
$\tilde {\phi }(\tilde {\boldsymbol{\mathsf{A}}}) = \boldsymbol {\nabla }\boldsymbol {\cdot }\tilde {\boldsymbol {F}}$ depend on the additional invariant ![]() $\widetilde {\mathcal {I}}_0$. The procedure to derive the vector field
$\widetilde {\mathcal {I}}_0$. The procedure to derive the vector field ![]() $\tilde {\boldsymbol {F}}$, detailed in § 4 for the incompressible gradient, applies to the compressible gradient with the modifications listed in Appendix B. With those modifications, the same procedure as outlined in § 4 yields for the compressible/perceived gradient
$\tilde {\boldsymbol {F}}$, detailed in § 4 for the incompressible gradient, applies to the compressible gradient with the modifications listed in Appendix B. With those modifications, the same procedure as outlined in § 4 yields for the compressible/perceived gradient
The average of the divergence of the vector field (6.1),
vanishes by homogeneity for all the arbitrary constants ![]() $\bar {f}_i$, thus recovering all the homogeneity relations derived in Yang et al. (Reference Yang, Pumir and Xu2020, Reference Yang, Fang, Fang, Pumir and Xu2022) and proving their completeness.
$\bar {f}_i$, thus recovering all the homogeneity relations derived in Yang et al. (Reference Yang, Pumir and Xu2020, Reference Yang, Fang, Fang, Pumir and Xu2022) and proving their completeness.
7. Conclusions
We have shown that the Betchov homogeneity relations are all the possible homogeneity constraints for the velocity gradient in incompressible and statistically isotropic turbulence. Our conclusions apply to the single-point statistics of scalar functions of the velocity gradient. Our approach also allows the derivation of homogeneity relations involving additional quantities, like the pressure Hessian and velocity gradient Laplacian. The presented methodology furthermore generalizes to derive homogeneity constraints for the compressible/perceived gradient, in two- and three-dimensional isotropic flows, as well as in less idealized (e.g. axisymmetric) flows. More generally, the outcome of these calculations will help to deal with high-dimensional tensor equations, which are ubiquitous in fluid dynamics.
Acknowledgements
We thank L. Bentkamp, A.D. Bragg, T.D. Drivas, M. Iovieno, P. Johnson, A. Pumir and H. Xu for insightful comments on the manuscript.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Tensor derivatives of the basis tensors and independent invariants
In this appendix, we compute the derivatives with respect to the incompressible gradient ![]() $\boldsymbol{\mathsf{A}}$ of the basis tensors
$\boldsymbol{\mathsf{A}}$ of the basis tensors ![]() $\boldsymbol{\mathsf{B}}^n$ (3.3) and invariants
$\boldsymbol{\mathsf{B}}^n$ (3.3) and invariants ![]() $\mathcal {I}_k$ (3.4).
$\mathcal {I}_k$ (3.4).
We start with the derivatives of the invariants (3.4), which can be expressed as linear combinations of the basis tensors, as in (4.2). The matrix ![]() $\boldsymbol{\mathsf{M}}$ featuring the components of the derivatives of the invariants (3.4) in the employed basis (3.3) is computed by contracting (4.2) with the basis tensors,
$\boldsymbol{\mathsf{M}}$ featuring the components of the derivatives of the invariants (3.4) in the employed basis (3.3) is computed by contracting (4.2) with the basis tensors,
 \begin{equation} M_{km} =
Z^{{-}1}_{ml}B^l_{pq}\frac{\partial \mathcal{I}_k}{\partial
A_{pq}}= \left[\begin{matrix} 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0
& 0\\ 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0\\ -
\mathcal{I}_{1} & 0 & 0 & 3 & 0 & 0 & 0 & 0 & 0\\ -
\tfrac{1}{3}\mathcal{I}_{2} & 0 & 0 & 0 & 0 & -1 & 1 & 0 &
0\\ - \tfrac{2}{3}\mathcal{I}_{4} & 0 & 0 & 0 & 0 & 0 & 0 &
1 & -1
\end{matrix}\right],\end{equation}
\begin{equation} M_{km} =
Z^{{-}1}_{ml}B^l_{pq}\frac{\partial \mathcal{I}_k}{\partial
A_{pq}}= \left[\begin{matrix} 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0
& 0\\ 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0\\ -
\mathcal{I}_{1} & 0 & 0 & 3 & 0 & 0 & 0 & 0 & 0\\ -
\tfrac{1}{3}\mathcal{I}_{2} & 0 & 0 & 0 & 0 & -1 & 1 & 0 &
0\\ - \tfrac{2}{3}\mathcal{I}_{4} & 0 & 0 & 0 & 0 & 0 & 0 &
1 & -1
\end{matrix}\right],\end{equation}
where ![]() $Z^{lm}=B^l_{pq}B^m_{pq}$ is the metric tensor and
$Z^{lm}=B^l_{pq}B^m_{pq}$ is the metric tensor and ![]() $\boldsymbol{\mathsf{Z}}^{-1}$ denotes its matrix inverse.
$\boldsymbol{\mathsf{Z}}^{-1}$ denotes its matrix inverse.
Next, we compute the derivatives of the basis tensors, for which we first introduce some notation. The basis tensors (3.3) are products of the symmetric and antisymmetric parts of the velocity gradient (3.1a,b), which can in turn be expressed through the fourth-order tensors
contracted with the gradient itself, ![]() $S_{ij}=Q^{(+1)}_{ijpq}A_{pq}$ and
$S_{ij}=Q^{(+1)}_{ijpq}A_{pq}$ and ![]() $W_{ij}=Q^{(-1)}_{ijpq}A_{pq}$. Then, any basis tensor (3.3) of degree
$W_{ij}=Q^{(-1)}_{ijpq}A_{pq}$. Then, any basis tensor (3.3) of degree ![]() $d$ consists of a linear combination of the products
$d$ consists of a linear combination of the products
with ![]() $t_l=\pm 1$ and summation over repeated indices, e.g.
$t_l=\pm 1$ and summation over repeated indices, e.g. ![]() $\boldsymbol{\mathsf{b}}^{+1,-1} = \boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{W}}$. Also, the components of the basis tensors (3.3) with respect to the elementary products (A3) are constant:
$\boldsymbol{\mathsf{b}}^{+1,-1} = \boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{W}}$. Also, the components of the basis tensors (3.3) with respect to the elementary products (A3) are constant:
e.g. the non-zero components of ![]() $\boldsymbol{\mathsf{B}}^4 = \boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{W}} - \boldsymbol{\mathsf{W}}\boldsymbol{\mathsf{S}}$ are
$\boldsymbol{\mathsf{B}}^4 = \boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{W}} - \boldsymbol{\mathsf{W}}\boldsymbol{\mathsf{S}}$ are ![]() $c^4_{+1,-1}=-c^4_{-1,+1}=1$.
$c^4_{+1,-1}=-c^4_{-1,+1}=1$.
Using (A3) and (A4) we can take the derivative of any basis tensor of degree ![]() $d$:
$d$:
 \begin{align} \frac{\partial B^{n}_{ij}}{\partial A_{pq}} &= \sum_{t_1t_2\cdots t_d} c_{t_1\cdots t_d}^n Q^{(t_1)}_{ik_1p_1q_1}Q^{(t_2)}_{k_1k_2p_2q_2} \cdots Q^{(t_d)}_{k_{d-1}j p_dq_d} \frac{\partial}{\partial A_{pq}} (A_{p_1q_1}A_{p_2q_2}\cdots A_{p_dq_d}) \nonumber\\ &= \sum_{t_1t_2\cdots t_d} c_{t_1\cdots t_d}^n \sum_{m=1}^d [b^{t_1 t_2 \cdots t_{m-1}}_{i k_{m-1}} Q^{(t_m)}_{k_{m-1}k_m pq} b^{t_{m+1}t_{m+2} \cdots t_d}_{k_mj} ], \end{align}
\begin{align} \frac{\partial B^{n}_{ij}}{\partial A_{pq}} &= \sum_{t_1t_2\cdots t_d} c_{t_1\cdots t_d}^n Q^{(t_1)}_{ik_1p_1q_1}Q^{(t_2)}_{k_1k_2p_2q_2} \cdots Q^{(t_d)}_{k_{d-1}j p_dq_d} \frac{\partial}{\partial A_{pq}} (A_{p_1q_1}A_{p_2q_2}\cdots A_{p_dq_d}) \nonumber\\ &= \sum_{t_1t_2\cdots t_d} c_{t_1\cdots t_d}^n \sum_{m=1}^d [b^{t_1 t_2 \cdots t_{m-1}}_{i k_{m-1}} Q^{(t_m)}_{k_{m-1}k_m pq} b^{t_{m+1}t_{m+2} \cdots t_d}_{k_mj} ], \end{align}
with ![]() $t_l=\pm 1$,
$t_l=\pm 1$, ![]() $k_0=i$,
$k_0=i$, ![]() $k_d=j$ and contraction over repeated indices. As expected, the derivative of any basis tensor consists of a linear combination of lower-order tensors. The derivative
$k_d=j$ and contraction over repeated indices. As expected, the derivative of any basis tensor consists of a linear combination of lower-order tensors. The derivative ![]() $\partial ( \cdot)/\partial A_{pq}$ is understood as a directional derivative in
$\partial ( \cdot)/\partial A_{pq}$ is understood as a directional derivative in ![]() $\mathbb {R}^{3,3}$ (Itskov Reference Itskov2015) and it is traceless due to incompressibility. In the steps to (A5), this property is taken into account by
$\mathbb {R}^{3,3}$ (Itskov Reference Itskov2015) and it is traceless due to incompressibility. In the steps to (A5), this property is taken into account by ![]() $\boldsymbol{\mathsf{Q}}^{(t)}$, since
$\boldsymbol{\mathsf{Q}}^{(t)}$, since ![]() $Q^{(t)}_{ijpq}\delta _{pq}=0$ (in fact,
$Q^{(t)}_{ijpq}\delta _{pq}=0$ (in fact, ![]() $\boldsymbol{\mathsf{Q}}^{(t)}$ is the tensor derivative of
$\boldsymbol{\mathsf{Q}}^{(t)}$ is the tensor derivative of ![]() $\boldsymbol{\mathsf{b}}^t$ with respect to
$\boldsymbol{\mathsf{b}}^t$ with respect to ![]() $\boldsymbol{\mathsf{A}}$).
$\boldsymbol{\mathsf{A}}$).
Inserting the expression of the fourth-order tensors (A2) into (A5), we can write the derivatives of the basis tensors more explicitly. For the basis tensors (3.3) of degree one (i.e. for ![]() $1\le n \le 2$), we have
$1\le n \le 2$), we have
 \begin{equation} \frac{\partial B^n_{ij}}{\partial A_{pq}} = \frac{1}{2}\sum_{t_1} c_{t_1}^n \left(\delta_{ip}\delta_{qj} + t_1\delta_{iq}\delta_{pj} -\frac{1+t_1}{3}\delta_{ij}\delta_{pq} \right). \end{equation}
\begin{equation} \frac{\partial B^n_{ij}}{\partial A_{pq}} = \frac{1}{2}\sum_{t_1} c_{t_1}^n \left(\delta_{ip}\delta_{qj} + t_1\delta_{iq}\delta_{pj} -\frac{1+t_1}{3}\delta_{ij}\delta_{pq} \right). \end{equation}
The derivatives of the basis tensors (3.3) of degree two (i.e. for ![]() $3\le n \le 6$) read
$3\le n \le 6$) read
 \begin{align} \frac{\partial B^n_{ij}}{\partial A_{pq}} &= \frac{1}{2}\sum_{t_1t_2}c_{t_1t_2}^n \left(\delta_{ip}b^{t_2}_{qj} + t_1\delta_{iq}b^{t_2}_{p j} -\frac{1+t_1}{3}b^{t_2}_{i j}\delta_{pq} \right.\nonumber\\ &\quad \left.+ \, b^{t_1}_{i p}\delta_{qj} + t_2 b^{t_1}_{i q}\delta_{pj} - \frac{1+t_2}{3}b^{t_1}_{i j}\delta_{pq}\right). \end{align}
\begin{align} \frac{\partial B^n_{ij}}{\partial A_{pq}} &= \frac{1}{2}\sum_{t_1t_2}c_{t_1t_2}^n \left(\delta_{ip}b^{t_2}_{qj} + t_1\delta_{iq}b^{t_2}_{p j} -\frac{1+t_1}{3}b^{t_2}_{i j}\delta_{pq} \right.\nonumber\\ &\quad \left.+ \, b^{t_1}_{i p}\delta_{qj} + t_2 b^{t_1}_{i q}\delta_{pj} - \frac{1+t_2}{3}b^{t_1}_{i j}\delta_{pq}\right). \end{align}
Finally, the derivatives of the basis tensors (3.3) of degree three (i.e. for ![]() $7\le n \le 8$) read
$7\le n \le 8$) read
 \begin{align} \frac{\partial B^n_{ij}}{\partial A_{pq}} &= \frac{1}{2}\sum_{t_1t_2t_3}c_{t_1t_2t_3}^n \left(\delta_{ip}b^{t_2 t_3}_{q j} + t_1\delta_{iq}b^{t_2 t_3}_{p j} - \frac{1+t_1}{3}b^{t_2 t_3}_{i j}\delta_{pq} + b^{t_1}_{i p}b^{t_3}_{q j} \right.\nonumber\\ &\quad \left.+ \, t_2b^{t_1}_{i q}b^{t_3}_{p j} -\frac{1+t_2}{3}b^{t_1t_3}_{ij} \delta_{pq} + b^{t_1 t_2}_{i p}\delta_{qj} + t_3b^{t_1 t_2}_{i q}\delta_{pj} - \frac{1+t_3}{3}b^{t_1 t_2}_{i j}\delta_{pq}\right). \end{align}
\begin{align} \frac{\partial B^n_{ij}}{\partial A_{pq}} &= \frac{1}{2}\sum_{t_1t_2t_3}c_{t_1t_2t_3}^n \left(\delta_{ip}b^{t_2 t_3}_{q j} + t_1\delta_{iq}b^{t_2 t_3}_{p j} - \frac{1+t_1}{3}b^{t_2 t_3}_{i j}\delta_{pq} + b^{t_1}_{i p}b^{t_3}_{q j} \right.\nonumber\\ &\quad \left.+ \, t_2b^{t_1}_{i q}b^{t_3}_{p j} -\frac{1+t_2}{3}b^{t_1t_3}_{ij} \delta_{pq} + b^{t_1 t_2}_{i p}\delta_{qj} + t_3b^{t_1 t_2}_{i q}\delta_{pj} - \frac{1+t_3}{3}b^{t_1 t_2}_{i j}\delta_{pq}\right). \end{align} After replacing the symmetric and antisymmetric parts of ![]() $\boldsymbol{\mathsf{b}}^{t_1}$ and
$\boldsymbol{\mathsf{b}}^{t_1}$ and ![]() $\boldsymbol{\mathsf{b}}^{t_1 t_2}$ with the corresponding
$\boldsymbol{\mathsf{b}}^{t_1 t_2}$ with the corresponding ![]() $\boldsymbol{\mathsf{B}}^n$, the tensor derivatives (A6), (A7) and (A8) can be compactly rewritten as contractions of the basis tensors with the Christoffel symbols
$\boldsymbol{\mathsf{B}}^n$, the tensor derivatives (A6), (A7) and (A8) can be compactly rewritten as contractions of the basis tensors with the Christoffel symbols ![]() $\varGamma ^{P,n}_{lm}$, as in (4.3) in the main text. For the tensor basis (3.3) employed here, the non-zero elements of
$\varGamma ^{P,n}_{lm}$, as in (4.3) in the main text. For the tensor basis (3.3) employed here, the non-zero elements of ![]() $\varGamma ^{1,n}_{lm}$ are
$\varGamma ^{1,n}_{lm}$ are
 \begin{equation} \left.\begin{gathered} \begin{aligned} \varGamma^{1,1}_{0 0} & = \tfrac{1}{2}, \\ \varGamma^{1,2}_{0 0} & = \tfrac{1}{2}, \\ \varGamma^{1,3}_{0 1} & = \tfrac{1}{2}, \\ \varGamma^{1,3}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{1,4}_{0 1} & ={-}\tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{1,4}_{0 2} & = \tfrac{1}{2}, \\ \varGamma^{1,4}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{1,4}_{2 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{1,5}_{0 1} & = \tfrac{1}{2}, \\ \varGamma^{1,5}_{0 2} & = \tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{1,5}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{1,5}_{2 0} & = \tfrac{1}{2}, \\ \varGamma^{1,6}_{0 2} & = \tfrac{1}{2}, \\ \varGamma^{1,6}_{2 0} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{0 4} & ={-}\tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{1,7}_{0 5} & = \tfrac{1}{4}, \\ \varGamma^{1,7}_{0 6} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{1 2} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{2 1} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{4 0} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{1,7}_{5 0} & = \tfrac{1}{4}, \\ \varGamma^{1,7}_{6 0} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{0 3} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{0 4} & = \tfrac{1}{4}, \\ \varGamma^{1,8}_{0 5} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{1,8}_{1 2} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{2 1} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{3 0} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{4 0} & ={-}\tfrac{1}{4}, \\ \varGamma^{1,8}_{5 0} & = \tfrac{1}{4}, \end{aligned} \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \begin{aligned} \varGamma^{1,1}_{0 0} & = \tfrac{1}{2}, \\ \varGamma^{1,2}_{0 0} & = \tfrac{1}{2}, \\ \varGamma^{1,3}_{0 1} & = \tfrac{1}{2}, \\ \varGamma^{1,3}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{1,4}_{0 1} & ={-}\tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{1,4}_{0 2} & = \tfrac{1}{2}, \\ \varGamma^{1,4}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{1,4}_{2 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{1,5}_{0 1} & = \tfrac{1}{2}, \\ \varGamma^{1,5}_{0 2} & = \tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{1,5}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{1,5}_{2 0} & = \tfrac{1}{2}, \\ \varGamma^{1,6}_{0 2} & = \tfrac{1}{2}, \\ \varGamma^{1,6}_{2 0} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{0 4} & ={-}\tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{1,7}_{0 5} & = \tfrac{1}{4}, \\ \varGamma^{1,7}_{0 6} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{1 2} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{2 1} & = \tfrac{1}{2}, \\ \varGamma^{1,7}_{4 0} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{1,7}_{5 0} & = \tfrac{1}{4}, \\ \varGamma^{1,7}_{6 0} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{0 3} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{0 4} & = \tfrac{1}{4}, \\ \varGamma^{1,8}_{0 5} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{1,8}_{1 2} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{2 1} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{3 0} & = \tfrac{1}{2}, \\ \varGamma^{1,8}_{4 0} & ={-}\tfrac{1}{4}, \\ \varGamma^{1,8}_{5 0} & = \tfrac{1}{4}, \end{aligned} \end{gathered}\right\} \end{equation}
the non-zero elements of ![]() $\varGamma ^{2,n}_{lm}$ are
$\varGamma ^{2,n}_{lm}$ are
 \begin{equation} \left.\begin{gathered} \begin{aligned} \varGamma^{2,1}_{0 0} & = \tfrac{1}{2}, \\ \varGamma^{2,2}_{0 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,3}_{0 1} & = \tfrac{1}{2}, \\ \varGamma^{2,3}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{2,4}_{0 1} & = \tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{2,4}_{0 2} & = \tfrac{1}{2}, \\ \varGamma^{2,4}_{1 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,4}_{2 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,5}_{0 1} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,5}_{0 2} & = \tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{2,5}_{1 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,5}_{2 0} & = \tfrac{1}{2}, \\ \varGamma^{2,6}_{0 2} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,6}_{2 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,7}_{0 4} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{2,7}_{0 5} & ={-}\tfrac{1}{4}, \\ \varGamma^{2,7}_{0 6} & = \tfrac{1}{2}, \\ \varGamma^{2,7}_{1 2} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,7}_{2 1} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,7}_{4 0} & ={-}\tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{2,7}_{5 0} & ={-}\tfrac{1}{4}, \\ \varGamma^{2,7}_{6 0} & = \tfrac{1}{2}, \\ \varGamma^{2,8}_{0 3} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,8}_{0 4} & = \tfrac{1}{4}, \\ \varGamma^{2,8}_{0 5} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{2,8}_{1 2} & = \tfrac{1}{2}, \\ \varGamma^{2,8}_{2 1} & = \tfrac{1}{2}, \\ \varGamma^{2,8}_{3 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,8}_{4 0} & ={-}\tfrac{1}{4}, \\ \varGamma^{2,8}_{5 0} & = \tfrac{1}{4}, \end{aligned} \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \begin{aligned} \varGamma^{2,1}_{0 0} & = \tfrac{1}{2}, \\ \varGamma^{2,2}_{0 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,3}_{0 1} & = \tfrac{1}{2}, \\ \varGamma^{2,3}_{1 0} & = \tfrac{1}{2}, \\ \varGamma^{2,4}_{0 1} & = \tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{2,4}_{0 2} & = \tfrac{1}{2}, \\ \varGamma^{2,4}_{1 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,4}_{2 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,5}_{0 1} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,5}_{0 2} & = \tfrac{1}{2}, \end{aligned}\quad \begin{aligned} \varGamma^{2,5}_{1 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,5}_{2 0} & = \tfrac{1}{2}, \\ \varGamma^{2,6}_{0 2} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,6}_{2 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,7}_{0 4} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{2,7}_{0 5} & ={-}\tfrac{1}{4}, \\ \varGamma^{2,7}_{0 6} & = \tfrac{1}{2}, \\ \varGamma^{2,7}_{1 2} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,7}_{2 1} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,7}_{4 0} & ={-}\tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{2,7}_{5 0} & ={-}\tfrac{1}{4}, \\ \varGamma^{2,7}_{6 0} & = \tfrac{1}{2}, \\ \varGamma^{2,8}_{0 3} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,8}_{0 4} & = \tfrac{1}{4}, \\ \varGamma^{2,8}_{0 5} & = \tfrac{1}{4}, \end{aligned}\quad \begin{aligned} \varGamma^{2,8}_{1 2} & = \tfrac{1}{2}, \\ \varGamma^{2,8}_{2 1} & = \tfrac{1}{2}, \\ \varGamma^{2,8}_{3 0} & ={-}\tfrac{1}{2}, \\ \varGamma^{2,8}_{4 0} & ={-}\tfrac{1}{4}, \\ \varGamma^{2,8}_{5 0} & = \tfrac{1}{4}, \end{aligned} \end{gathered}\right\} \end{equation}
and the non-zero elements of ![]() $\varGamma ^{3,n}_{lm}$ are
$\varGamma ^{3,n}_{lm}$ are
To obtain (4.3) from (A6), (A7) and (A8), we first computed the Christoffel symbols relative to ![]() $\{\boldsymbol{\mathsf{b}}^{t_1},\boldsymbol{\mathsf{b}}^{t_1t_2},\boldsymbol{\mathsf{b}}^{t_1t_2t_3}\}$ and then changed the basis to the
$\{\boldsymbol{\mathsf{b}}^{t_1},\boldsymbol{\mathsf{b}}^{t_1t_2},\boldsymbol{\mathsf{b}}^{t_1t_2t_3}\}$ and then changed the basis to the ![]() $\{\boldsymbol{\mathsf{B}}^n\}$ in (3.3). Indeed, any set of basis tensors can be expressed through the transformation
$\{\boldsymbol{\mathsf{B}}^n\}$ in (3.3). Indeed, any set of basis tensors can be expressed through the transformation ![]() $\hat {\boldsymbol{\mathsf{B}}}^{n'}=T^{n'}_n(\mathcal {I}) \boldsymbol{\mathsf{B}}^{n}$, with
$\hat {\boldsymbol{\mathsf{B}}}^{n'}=T^{n'}_n(\mathcal {I}) \boldsymbol{\mathsf{B}}^{n}$, with ![]() $\boldsymbol{\mathsf{T}}$ an invertible matrix function of the invariants. Then, the Christoffel symbols transform as
$\boldsymbol{\mathsf{T}}$ an invertible matrix function of the invariants. Then, the Christoffel symbols transform as
 \begin{equation} \left.\begin{gathered} \hat{\varGamma}^{1,n'}_{l'm'} = T^{n'}_n \varGamma^{1,n}_{lm} (T^{{-}1})^l_{l'} (T^{{-}1})^m_{m'}, \quad \hat{\varGamma}^{2,n'}_{l'm'} = T^{n'}_n \varGamma^{2,n}_{lm} (T^{{-}1})^l_{l'} (T^{{-}1})^m_{m'}, \\ \hat{\varGamma}^{3,n'}_{l'm'} = \left(T^{n'}_n \varGamma^{3,n}_{lm} + \frac{\partial T^{n'}_l}{\partial \mathcal{I}_k}M_{km}\right) (T^{{-}1})^l_{l'}(T^{{-}1})^m_{m'}. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \hat{\varGamma}^{1,n'}_{l'm'} = T^{n'}_n \varGamma^{1,n}_{lm} (T^{{-}1})^l_{l'} (T^{{-}1})^m_{m'}, \quad \hat{\varGamma}^{2,n'}_{l'm'} = T^{n'}_n \varGamma^{2,n}_{lm} (T^{{-}1})^l_{l'} (T^{{-}1})^m_{m'}, \\ \hat{\varGamma}^{3,n'}_{l'm'} = \left(T^{n'}_n \varGamma^{3,n}_{lm} + \frac{\partial T^{n'}_l}{\partial \mathcal{I}_k}M_{km}\right) (T^{{-}1})^l_{l'}(T^{{-}1})^m_{m'}. \end{gathered}\right\} \end{equation}Appendix B. Modifications for compressible or perceived velocity gradients
As for the incompressible gradient, all the homogeneity relations for a compressible or perceived gradient ![]() $\tilde {\boldsymbol{\mathsf{A}}}$ follow from (2.4), with
$\tilde {\boldsymbol{\mathsf{A}}}$ follow from (2.4), with ![]() $v_i\equiv 0$ in the compressible/perceived case. This is because
$v_i\equiv 0$ in the compressible/perceived case. This is because ![]() $\boldsymbol {\nabla }\tilde {\boldsymbol{\mathsf{A}}}$ has no identically zero contractions. To derive homogeneity constraints for the compressible gradient, we follow the same steps as outlined in § 4, now employing the appropriate Christoffel symbols
$\boldsymbol {\nabla }\tilde {\boldsymbol{\mathsf{A}}}$ has no identically zero contractions. To derive homogeneity constraints for the compressible gradient, we follow the same steps as outlined in § 4, now employing the appropriate Christoffel symbols ![]() $\tilde {\varGamma }^{P,n}_{lm}$ and derivative components
$\tilde {\varGamma }^{P,n}_{lm}$ and derivative components ![]() $\tilde {M}_{km}$, characterizing the tensor derivatives of the compressible/perceived basis tensors and invariants. In this appendix we compute
$\tilde {M}_{km}$, characterizing the tensor derivatives of the compressible/perceived basis tensors and invariants. In this appendix we compute ![]() $\tilde {\varGamma }^{P,n}_{lm}$ and
$\tilde {\varGamma }^{P,n}_{lm}$ and ![]() $\tilde {M}_{km}$.
$\tilde {M}_{km}$.
The basis tensors (3.3) are the same for the incompressible and compressible/perceived gradient, while the independent invariants ![]() $\widetilde {\mathcal {I}}_k$ (3.4) feature the additional invariant
$\widetilde {\mathcal {I}}_k$ (3.4) feature the additional invariant ![]() $\widetilde {\mathcal {I}}_0=\textrm {Tr}(\tilde {\boldsymbol{\mathsf{A}}})$ in the compressible/perceived case. The contributions from incompressibility to the tensor derivatives (4.2) and (4.3) vanish for a compressible/perceived gradient. This implies that
$\widetilde {\mathcal {I}}_0=\textrm {Tr}(\tilde {\boldsymbol{\mathsf{A}}})$ in the compressible/perceived case. The contributions from incompressibility to the tensor derivatives (4.2) and (4.3) vanish for a compressible/perceived gradient. This implies that ![]() $\tilde {\varGamma }^{3,n}_{lm}=0$, while
$\tilde {\varGamma }^{3,n}_{lm}=0$, while ![]() $\tilde {\varGamma }^{1,n}_{lm}=\varGamma ^{1,n}_{lm}$ and
$\tilde {\varGamma }^{1,n}_{lm}=\varGamma ^{1,n}_{lm}$ and ![]() $\tilde {\varGamma }^{2,n}_{lm}=\varGamma ^{2,n}_{lm}$. The matrix of the derivatives of the invariants is
$\tilde {\varGamma }^{2,n}_{lm}=\varGamma ^{2,n}_{lm}$. The matrix of the derivatives of the invariants is
 \begin{equation} \tilde{M}_{km} = Z^{{-}1}_{ml}B^l_{pq} \frac{\partial \widetilde{\mathcal{I}}_k}{\partial \tilde{A}_{pq}}= \left[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 3 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \end{matrix}\right], \end{equation}
\begin{equation} \tilde{M}_{km} = Z^{{-}1}_{ml}B^l_{pq} \frac{\partial \widetilde{\mathcal{I}}_k}{\partial \tilde{A}_{pq}}= \left[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & -2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 3 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \end{matrix}\right], \end{equation}
where the first row refers to ![]() $\widetilde {\mathcal {I}}_0$, and the first column is now zero for
$\widetilde {\mathcal {I}}_0$, and the first column is now zero for ![]() $k>0$ since the tensor derivatives of the invariants
$k>0$ since the tensor derivatives of the invariants ![]() $\partial \widetilde {\mathcal {I}}_k/\partial \tilde {\boldsymbol{\mathsf{A}}}$ are no longer traceless.
$\partial \widetilde {\mathcal {I}}_k/\partial \tilde {\boldsymbol{\mathsf{A}}}$ are no longer traceless.