Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-31T16:04:25.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory flow regimes for a circular cylinder near a plane boundary

Published online by Cambridge University Press:  04 April 2018

Chengwang Xiong Open the ORCID record for Chengwang Xiong [Opens in a new window] ,
Liang Cheng ,
Feifei Tong  and
Hongwei An Open the ORCID record for Hongwei An [Opens in a new window]
Chengwang Xiong
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia School of Civil Engineering, Hebei University of Technology, Tianjin, 300401, China
Liang Cheng*
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, No. 2 Linggong Road, Dalian 116024, China
Feifei Tong
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Hongwei An
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: liang.cheng@uwa.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Oscillatory flow around a circular cylinder close to a plane boundary is numerically investigated at low-to-intermediate Keulegan–Carpenter (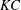$KC$) and Stokes numbers (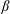$\unicode[STIX]{x1D6FD}$) for different gap-to-diameter ratios (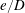$e/D$). A set of unique flow regimes is observed and classified based on the established nomenclature in the (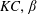$KC,\unicode[STIX]{x1D6FD}$)-space. It is found that the flow is not only influenced by 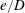$e/D$ but also by the ratio of the thickness of the Stokes boundary layer (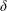$\unicode[STIX]{x1D6FF}$) to the gap size (e). At relatively large 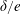$\unicode[STIX]{x1D6FF}/e$ values, vortex shedding through the gap is suppressed and vortices are only shed from the top of the cylinder. At intermediate values of 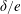$\unicode[STIX]{x1D6FF}/e$, flow through the gap is enhanced, resulting in horizontal gap vortex shedding. As 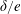$\unicode[STIX]{x1D6FF}/e$ is further reduced below a critical value, the influence of 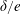$\unicode[STIX]{x1D6FF}/e$ becomes negligible and the flow is largely dependent on 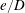$e/D$. A hysteresis phenomenon is observed for the transitions in the flow regime. The physical mechanisms responsible for the hysteresis and the variation of marginal stability curves with 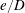$e/D$ are explored at $KC=6$ through specifically designed numerical simulations. The Stokes boundary layer over the plane boundary is found to be responsible for the relatively large hysteresis range over 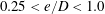$0.25<e/D<1.0$. Three mechanisms have been identified to the change of the marginal stability curve over 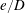$e/D$, which are the blockage effect due to the geometry setting, the favourable pressure gradient over the gap and the location of the leading eigenmode relative to the cylinder.

JFM classification

Instability: Absolute/convective instability Boundary Layers: Boundary layer structure

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 127 - 161
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

An, H., Cheng, L. & Zhao, M. 2010 Steady streaming around a circular cylinder near a plane boundary due to oscillatory flow. J. Hydraul. Engng 137 (1), 23–33.10.1061/(ASCE)HY.1943-7900.0000258Google Scholar
Anagnostopoulos, P. & Minear, R. 2004 Blockage effect of oscillatory flow past a fixed cylinder. Appl. Ocean Res. 26 (3), 147–153.10.1016/j.apor.2004.11.001Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.10.1017/S0022112096002777Google Scholar
Bearman, P. W., Downie, M. J., Graham, J. M. R. & Obasaju, E. D. 1985 Forces on cylinders in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 154, 337–356.10.1017/S0022112085001562Google Scholar
Blackburn, H. M. & Henderson, R. D. 1999 A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 385, 255–286.10.1017/S0022112099004309Google Scholar
Bolis, A.2013 Fourier spectral/ $hp$ element method: investigation of time-stepping and parallelisation strategies. PhD thesis.Google Scholar
Cantwell, C. D., Moxey, D., Comerford, A, Bolis, A., Rocco, G., Mengaldo, G., De Grazia, D., Yakovlev, S., Lombard, J-E, Ekelschot, D. et al. 2015 Nektar + +: An open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.10.1016/j.cpc.2015.02.008Google Scholar
Carstensen, S., Sumer, B. M. & Fredsøe, J. 2010 Coherent structures in wave boundary layers. Part 1. Oscillatory motion. J. Fluid Mech. 646, 169–206.10.1017/S0022112009992825Google Scholar
Dütsch, H., Durst, F., Becker, S. & Lienhart, H. 1998 Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers. J. Fluid Mech. 360, 249–271.10.1017/S002211209800860XGoogle Scholar
Elston, J. R., Blackburn, H. M. & Sheridan, J. 2006 The primary and secondary instabilities of flow generated by an oscillating circular cylinder. J. Fluid Mech. 550, 359–389.10.1017/S0022112005008372Google Scholar
Elston, J. R., Sheridan, J. & Blackburn, H. M. 2004 Two-dimensional Floquet stability analysis of the flow produced by an oscillating circular cylinder in quiescent fluid. Eur. J. Mech. (B/Fluids) 23 (1), 99–106.10.1016/j.euromechflu.2003.05.002Google Scholar
Henderson, R. D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8 (6), 1683–1685.10.1063/1.868939Google Scholar
Hussain, A. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.10.1017/S0022112086001192Google Scholar
Jacobsen, V., Bryndum, M. B., Fredsøe, J. et al. 1984 Determination of flow kinematics close to marine’ pipelines and their use in stability calculations. In Offshore Technology Conference, Offshore Technology Conference.Google Scholar
Justesen, P. 1991 A numerical study of oscillating flow around a circular cylinder. J. Fluid Mech. 222, 157–196.10.1017/S0022112091001040Google Scholar
Kozakiewicz, A., Sumer, B. M. & Fredsøe, J. 1992 Spanwise correlation on a vibrating cylinder near a wall in oscillatory flows. J. Fluid Strcut. 6 (3), 371–392.10.1016/0889-9746(92)90015-UGoogle Scholar
Mouazé, D. & Bélorgey, M. 2003 Flow visualisation around a horizontal cylinder near a plane wall and subject to waves. Appl. Ocean Res. 25 (4), 195–211.10.1016/j.apor.2004.01.001Google Scholar
Nehari, D., Armenio, V. & Ballio, F. 2004 Three-dimensional analysis of the unidirectional oscillatory flow around a circular cylinder at low Keulegan–Carpenter and 𝛽 numbers. J. Fluid Mech. 520, 157–186.10.1017/S002211200400134XGoogle Scholar
Obasaju, E. D., Bearman, P. W. & Graham, J. M. R. 1988 A study of forces, circulation and vortex patterns around a circular cylinder in oscillating flow. J. Fluid Mech. 196, 467–494.10.1017/S0022112088002782Google Scholar
Rao, A., Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2011 Flows past rotating cylinders next to a wall. J. Fluids Struct. 27 (5), 668–679.10.1016/j.jfluidstructs.2011.03.019Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013 The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.10.1016/j.jfluidstructs.2012.08.007Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2015 Flow past a rotating cylinder translating at different gap heights along a wall. J. Fluids Struct. 57, 314–330.10.1016/j.jfluidstructs.2015.06.015Google Scholar
Sarpkaya, T. 1976 Forces on cylinders near a plane boundary. J. Fluids Engng 98 (3), 499.10.1115/1.3448383Google Scholar
Scandura, P., Armenio, V. & Foti, E. 2009 Numerical investigation of the oscillatory flow around a circular cylinder close to a wall at moderate Keulegan-Carpenter and low Reynolds numbers. J. Fluid Mech. 627, 259–290.10.1017/S0022112009006016Google Scholar
Shen, L. & Chan, E. 2013 Numerical simulation of oscillatory flows over a rippled bed by immersed boundary method. Appl. Ocean Res. 43, 27–36.10.1016/j.apor.2013.07.005Google Scholar
Sumer, B. M. & Fredsøe, J. 1997 Hydrodynamics Around Cylindrical Structures. World Scientific.10.1142/3316Google Scholar
Sumer, B. M., Jensen, B. L. & Fredsøe, J. 1991 Effect of a plane boundary on oscillatory flow around a circular cylinder. J. Fluid Mech. 225, 271–300.10.1017/S0022112091002057Google Scholar
Tatsuno, M. & Bearman, P. W. 1990 A visual study of the flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers and low Stokes numbers. J. Fluid Mech. 211, 157–182.10.1017/S0022112090001537Google Scholar
Tong, F., Cheng, L., Xiong, C., Draper, S., An, H. & Lou, X. 2017 Flow regimes for a square cross-section cylinder in oscillatory flow. J. Fluid Mech. 813, 85–109.10.1017/jfm.2016.829Google Scholar
Tong, F., Cheng, L., Zhao, M. & An, H. 2015 Oscillatory flow regimes around four cylinders in a square arrangement under small KC and Re conditions. J. Fluid Mech. 769, 298–336.10.1017/jfm.2015.107Google Scholar
Williamson, C. H. K. 1985 Sinusoidal flow relative to circular cylinders. J. Fluid Mech. 155, 141–174.10.1017/S0022112085001756Google Scholar
Zdravkovich, M. M. 1985 Forces on a circular cylinder near a plane wall. Appl. Ocean Res. 7 (4), 197–201.10.1016/0141-1187(85)90026-4Google Scholar
Zhao, M. & Cheng, L. 2014 Two-dimensional numerical study of vortex shedding regimes of oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds numbers. J. Fluid Mech. 751, 1–37.10.1017/jfm.2014.268Google Scholar

Xiong et al. supplementary movie 1

Animation of streakline in regime HA at (e/D, KC, β)=(0.25,10, 10).

Download Xiong et al. supplementary movie 1(Video)
Video 5.6 MB

Xiong et al. supplementary movie 2

Animation of streakline in regime GVS at (e/D, KC, β)=(0.5, 6, 20).

Download Xiong et al. supplementary movie 2(Video)
Video 3.3 MB

Xiong et al. supplementary movie 3

Animation of streakline in regime GVS-A at (e/D, KC, β)=(0.5, 6, 30).

Download Xiong et al. supplementary movie 3(Video)
Video 3.2 MB

Xiong et al. supplementary movie 4

Animation of streakline in regime E at (e/D, KC, β)=(2, 6, 30).

Download Xiong et al. supplementary movie 4(Video)
Video 3.3 MB

Xiong et al. supplementary movie 5

Animation of streakline in regime F' at (e/D, KC, β)=(0.25, 11, 20).

Download Xiong et al. supplementary movie 5(Video)
Video 4.3 MB

Xiong et al. supplementary movie 6

Animation of streakline in regime F at (e/D, KC, β)=(2, 10, 20).

Download Xiong et al. supplementary movie 6(Video)
Video 7 MB