Article contents
A parallel stability analysis of a trailing vortex wake
Published online by Cambridge University Press: 05 January 2018
Abstract
Trailing vortices are generated in aeronautical and maritime applications and produce a variety of adverse effects that remain difficult to control. A stability analysis can direct flow control designers towards pertinent frequencies, wavelengths and locations that may lead to the excitation of instabilities, resulting in the eventual breakup of the vortex. Most models for trailing vortices, however, are far-field models, making implementation of the findings from stability analyses challenging. As such, we perform a stability analysis in the formative region where the numerically computed base flow contains both a two-dimensional wake and a tip vortex generated from a NACA0012 at a 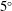 $5^{\circ }$ angle of attack and a chord-based Reynolds number of
$5^{\circ }$ angle of attack and a chord-based Reynolds number of 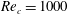 $Re_{c}=1000$. The parallel temporal and spatial analyses show that at three chord lengths downstream of the trailing edge, seven unstable modes are present: three stemming from the temporal analysis and four arising in the spatial analysis. The three temporal instabilities are analogues to three unstable modes in the spatial analysis, with the wake instability dominating in both analyses. The helical mode localized to the vortex co-rotates with the base flow, which is converse with the counter-rotating
$Re_{c}=1000$. The parallel temporal and spatial analyses show that at three chord lengths downstream of the trailing edge, seven unstable modes are present: three stemming from the temporal analysis and four arising in the spatial analysis. The three temporal instabilities are analogues to three unstable modes in the spatial analysis, with the wake instability dominating in both analyses. The helical mode localized to the vortex co-rotates with the base flow, which is converse with the counter-rotating 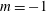 $m=-1$ instabilities of a Batchelor vortex model, which may be a result of the formative nature of the base-flow vortex. The fourth spatial mode is localized to the tip vortex region. The continuous part of the spectrum contains oscillatory and wavepacket solutions prompting the utilization of a wavepacket analysis to analyse the flow field and group velocity. The structure and details of the full bi-global spectrum will help navigate the design space of effective control strategies to hasten decay of persistent wingtip vortices.
$m=-1$ instabilities of a Batchelor vortex model, which may be a result of the formative nature of the base-flow vortex. The fourth spatial mode is localized to the tip vortex region. The continuous part of the spectrum contains oscillatory and wavepacket solutions prompting the utilization of a wavepacket analysis to analyse the flow field and group velocity. The structure and details of the full bi-global spectrum will help navigate the design space of effective control strategies to hasten decay of persistent wingtip vortices.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Edstrand et al. supplementary movie 1
Movie of the streamwise vorticity of the temporal principal wake instability.
Edstrand et al. supplementary movie 2
Movie of the streamwise vorticity of the temporal wake instability.
Edstrand et al. supplementary movie 3
Movie of the streamwise vorticity of the temporal vortex instability.
Edstrand et al. supplementary movie 4
Movie of the streamwise vorticity of the stable temporal vortex mode.
Edstrand et al. supplementary movie 5
Movie of the streamwise vorticity of the stable temporal wake mode.
Edstrand et al. supplementary movie 6
Movie of the streamwise vorticity of the spatial principal wake instability.
Edstrand et al. supplementary movie 7
Movie of the streamwise vorticity of the spatial wake instability.
Edstrand et al. supplementary movie 8
Movie of the streamwise vorticity of the spatial vortex instability.
- 31
- Cited by

