Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-01T04:27:37.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Pattern evolution and modal decomposition of Faraday waves in a brimful cylinder

Published online by Cambridge University Press:  10 November 2023

Shimin Zhang Open the ORCID record for Shimin Zhang [Opens in a new window] ,
Alistair G.L. Borthwick Open the ORCID record for Alistair G.L. Borthwick [Opens in a new window]  and
Zhiliang Lin Open the ORCID record for Zhiliang Lin [Opens in a new window]
Shimin Zhang
Affiliation:
State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China Marine Numerical Experiment Center, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Alistair G.L. Borthwick
Affiliation:
School of Engineering, The University of Edinburgh, The King's Buildings, Edinburgh EH9 3FB, UK School of Engineering, Computing and Mathematics, University of Plymouth, Plymouth PL4 8AA, UK
Zhiliang Lin*
Affiliation:
State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China Marine Numerical Experiment Center, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
*
†Email address for correspondence: linzhiliang@sjtu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

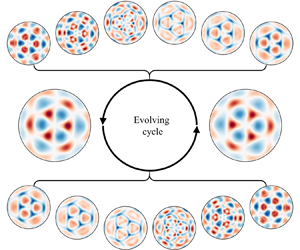
This paper investigates the steady-state pattern evolution of symmetric Faraday waves excited in a brimful cylindrical container when driving parameters much exceed critical thresholds. In such liquid systems, parametric surface responses are typically considered as the resonant superposition of unstable standing waves. A modified free-surface synthetic Schlieren method is employed to obtain full three-dimensional spatial reconstructions of instantaneous surface patterns. Multi-azimuth structures and localized travelling waves during the small-elevation phases of the oscillation cycle give rise to modal decomposition in the form of $\nu$-basis modes. Two-step surface-fitting results provide insight into the spatiotemporal characteristics of dominant wave components and corresponding harmonics in the experimental observations. Arithmetic combination of modal indices and uniform frequency distributions reveal the nonlinear mechanisms behind pattern formation and the primary pathways of energy transfer. Taking the hypothetical surface manifestation of multiple azimuths as the modal solutions, a linear stability analysis of the inviscid system is utilised to calculate fundamental resonance tongues (FRTs) with non-overlapping bottoms, which correspond to subharmonic or harmonic $\nu$-basis modes induced by surface instability at the air–liquid interface. Close relationships between experimental observations and corresponding FRTs provide qualitative verification of dominant modes identified using surface-fitting results. This supports the validity and rationality of the applied $\nu$-basis modes.

JFM classification

Waves/Free-surface Flows: Faraday waves Nonlinear Dynamical Systems: Pattern formation Instability: Parametric instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 974 , 10 November 2023 , A56
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abella, A.P. & Soriano, M.N. 2019 Detection and visualization of water surface three-wave resonance via a synthetic Schlieren method. Phys. Scr. 94 (3), 034006.CrossRefGoogle Scholar
Batson, W., Zoueshtiagh, F. & Narayanan, R. 2013 The Faraday threshold in small cylinders and the sidewall non-ideality. J. Fluid Mech. 729, 496–523.CrossRefGoogle Scholar
Bechhoefer, J., Ego, V., Manneville, S. & Johnson, B. 1995 An experimental study of the onset of parametrically pumped surface waves in viscous fluids. J. Fluid Mech. 288, 325–350.CrossRefGoogle Scholar
Benjamin, T.B. & Ursell, F.J. 1954 The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. A 225 (1163), 505–515.Google Scholar
Berhanu, M. & Falcon, E. 2013 Space-time-resolved capillary wave turbulence. Phys. Rev. E 87 (3), 033003.CrossRefGoogle Scholar
Binks, D. & van de Water, W. 1997 Nonlinear pattern formation of Faraday waves. Phys. Rev. Lett. 78 (21), 4043.CrossRefGoogle Scholar
Bongarzone, A., Viola, F., Camarri, S. & Gallaire, F. 2022 Subharmonic parametric instability in nearly brimful circular cylinders: a weakly nonlinear analysis. J. Fluid Mech. 947, A24.CrossRefGoogle Scholar
Bosch, E., Lambermont, H. & van de Water, W. 1994 Average patterns in Faraday waves. Phys. Rev. E 49 (5), R3580.CrossRefGoogle ScholarPubMed
Bostwick, J.B. & Steen, P.H. 2015 Stability of constrained capillary surfaces. Annu. Rev. Fluid Mech. 47, 539–568.CrossRefGoogle Scholar
Chen, P. & Viñals, J. 1999 Amplitude equation and pattern selection in Faraday waves. Phys. Rev. E 60 (1), 559.CrossRefGoogle ScholarPubMed
Christiansen, B., Alstrøm, P. & Levinsen, M.T. 1995 Dissipation and ordering in capillary waves at high aspect ratios. J. Fluid Mech. 291, 323–341.CrossRefGoogle Scholar
Christiansen, B., Alstrøm, P. & Levinsen, M.T. 1992 Ordered capillary-wave states: quasicrystals, hexagons, and radial waves. Phys. Rev. Lett. 68 (14), 2157.CrossRefGoogle Scholar
Ciliberto, S. & Gollub, J.P. 1984 Pattern competition leads to chaos. Phys. Rev. Lett. 52 (11), 922.CrossRefGoogle Scholar
Ciliberto, S. & Gollub, J.P. 1985 a Chaotic mode competition in parametrically forced surface waves. J. Fluid Mech. 158, 381–398.CrossRefGoogle Scholar
Ciliberto, S. & Gollub, J.P. 1985 b Phenomenological model of chaotic mode competition in surface waves. Il Nuovo Cimento D 6 (4), 309–316.CrossRefGoogle Scholar
Cobelli, P.J., Maurel, A., Pagneux, V. & Petitjeans, P. 2009 Global measurement of water waves by Fourier transform profilometry. Exp. Fluids 46 (6), 1037–1047.CrossRefGoogle Scholar
Crawford, J.D. 1991 Surface waves in nonsquare containers with square symmetry. Phys. Rev. Lett. 67 (4), 441.CrossRefGoogle ScholarPubMed
Crawford, J.D., Gollub, J.P. & Lane, D. 1993 Hidden symmetries of parametrically forced waves. Nonlinearity 6 (2), 119.CrossRefGoogle Scholar
Cross, M.C. & Hohenberg, P.C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851.CrossRefGoogle Scholar
Dalziel, S.B., Hughes, G.O. & Sutherland, B.R. 2000 Whole-field density measurements by ‘synthetic Schlieren’. Exp. Fluids 28 (4), 322–335.CrossRefGoogle Scholar
Damiano, A.P., Brun, P.-T., Harris, D.M., Galeano-Rios, C.A. & Bush, J.W.M. 2016 Surface topography measurements of the bouncing droplet experiment. Exp. Fluids 57 (10), 1–7.CrossRefGoogle Scholar
Das, S.P. & Hopfinger, E.J. 2008 Parametrically forced gravity waves in a circular cylinder and finite-time singularity. J. Fluid Mech. 599, 205–228.CrossRefGoogle Scholar
Douady, S. 1990 Experimental study of the Faraday instability. J. Fluid Mech. 221, 383–409.CrossRefGoogle Scholar
Falcon, E. & Mordant, N. 2022 Experiments in surface gravity–capillary wave turbulence. Annu. Rev. Fluid Mech. 54, 1–25.CrossRefGoogle Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. 121, 299–340.Google Scholar
Gollub, J.P. & Meyer, C.W. 1983 Symmetry-breaking instabilities on a fluid surface. Physica D 6 (3), 337–346.CrossRefGoogle Scholar
Hammack, J.L. & Henderson, D.M. 1993 Resonant interactions among surface water waves. Annu. Rev. Fluid Mech. 25 (1), 55–97.CrossRefGoogle Scholar
Haudin, F., Cazaubiel, A., Deike, L., Jamin, T., Falcon, E. & Berhanu, M. 2016 Experimental study of three-wave interactions among capillary-gravity surface waves. Phys. Rev. E 93 (4), 043110.CrossRefGoogle ScholarPubMed
Henderson, D.M. & Miles, J.W. 1990 Single-mode Faraday waves in small cylinders. J. Fluid Mech. 213, 95–109.CrossRefGoogle Scholar
Henderson, D.M. & Miles, J.W. 1991 Faraday waves in $2:1$ internal resonance. J. Fluid Mech. 222, 449–470.CrossRefGoogle Scholar
Hill, G.W. 1886 On the part of the motion of the lunar perigee which is a function of the mean motions of the sun and moon. Acta Math. 8 (1), 1–36.CrossRefGoogle Scholar
Kharbedia, M., Caselli, N., Herráez-Aguilar, D., López-Menéndez, H., Enciso, E., Santiago, J.A. & Monroy, F. 2021 Moulding hydrodynamic 2D-crystals upon parametric Faraday waves in shear-functionalized water surfaces. Nat. Commun. 12 (1), 1–11.CrossRefGoogle ScholarPubMed
Kidambi, R. 2009 Meniscus effects on the frequency and damping of capillary-gravity waves in a brimful circular cylinder. Wave Motion 46 (2), 144–154.CrossRefGoogle Scholar
Kidambi, R. 2013 Inviscid Faraday waves in a brimful circular cylinder. J. Fluid Mech. 724, 671–694.CrossRefGoogle Scholar
Kudrolli, A. & Gollub, J.P. 1996 Patterns and spatiotemporal chaos in parametrically forced surface waves: a systematic survey at large aspect ratio. Physica D 97 (1-3), 133–154.CrossRefGoogle Scholar
Kumar, K. 1996 Linear theory of Faraday instability in viscous liquids. Proc. R. Soc. Lond. A 452 (1948), 1113–1126.Google Scholar
Kumar, K. & Bajaj, K.M.S. 1995 Competing patterns in the Faraday experiment. Phys. Rev. E 52 (5), R4606.CrossRefGoogle ScholarPubMed
Kumar, K. & Tuckerman, L.S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.CrossRefGoogle Scholar
Kurata, J., Grattan, K.T.V., Uchiyama, H. & Tanaka, T. 1990 Water surface measurement in a shallow channel using the transmitted image of a grating. Rev. Sci. Instrum. 61 (2), 736–739.CrossRefGoogle Scholar
Lioubashevski, O., Fineberg, J. & Tuckerman, L.S. 1997 Scaling of the transition to parametrically driven surface waves in highly dissipative systems. Phys. Rev. E 55 (4), R3832.CrossRefGoogle Scholar
McLachlan, N.W. 1951 Theory and Application of Mathieu Functions. Oxford University Press.Google Scholar
Meron, E. 1987 Parametric excitation of multimode dissipative systems. Phys. Rev. A 35 (11), 4892.CrossRefGoogle ScholarPubMed
Meron, E. & Procaccia, I. 1986 Low-dimensional chaos in surface waves: theoretical analysis of an experiment. Phys. Rev. A 34 (4), 3221.CrossRefGoogle ScholarPubMed
Miles, J. & Henderson, D. 1990 Parametrically forced surface waves. Annu. Rev. Fluid Mech. 22 (1), 143–165.CrossRefGoogle Scholar
Milner, S.T. 1991 Square patterns and secondary instabilities in driven capillary waves. J. Fluid Mech. 225, 81–100.CrossRefGoogle Scholar
Moisy, F., Michon, G.-J., Rabaud, M. & Sultan, E. 2012 Cross-waves induced by the vertical oscillation of a fully immersed vertical plate. Phys. Fluids 24 (2), 022110.CrossRefGoogle Scholar
Moisy, F., Rabaud, M. & Salsac, K. 2009 A synthetic Schlieren method for the measurement of the topography of a liquid interface. Exp. Fluids 46 (6), 1021–1036.CrossRefGoogle Scholar
Müller, H.W., Wittmer, H., Wagner, C., Albers, J. & Knorr, K. 1997 Analytic stability theory for faraday waves and the observation of the harmonic surface response. Phys. Rev. Lett. 78 (12), 2357.CrossRefGoogle Scholar
Nayfeh, A.H. & Mook, D.T. 1995 Nonlinear Oscillations. John Wiley & Sons.CrossRefGoogle Scholar
Peters, F. 1985 Schlieren interferometry applied to a gravity wave in a density-stratified liquid. Exp. Fluids 3 (5), 261–269.CrossRefGoogle Scholar
Phillips, O.M. 1981 Wave interactions-the evolution of an idea. J. Fluid Mech. 106, 215–227.CrossRefGoogle Scholar
Puthenveettil, B.A. & Hopfinger, E.J. 2009 Evolution and breaking of parametrically forced capillary waves in a circular cylinder. J. Fluid Mech. 633, 355–379.CrossRefGoogle Scholar
Rajchenbach, J. & Clamond, D. 2015 Faraday waves: their dispersion relation, nature of bifurcation and wavenumber selection revisited. J. Fluid Mech. 777, R2.CrossRefGoogle Scholar
Rajchenbach, J., Clamond, D. & Leroux, A. 2013 Observation of star-shaped surface gravity waves. Phys. Rev. Lett. 110 (9), 094502.CrossRefGoogle ScholarPubMed
Rayleigh, Lord 1883 a VII. On the crispations of fluid resting upon a vibrating support. Lond. Edinb. Dublin Phil. Mag. J. Sci. 16 (97), 50–58.CrossRefGoogle Scholar
Rayleigh, Lord 1883 b XXXIII. On maintained vibrations. Lond. Edinb. Dublin Phil. Mag. J. Sci. 15 (94), 229–235.CrossRefGoogle Scholar
Shao, X., Wilson, P., Bostwick, J.B. & Saylor, J.R. 2021 a Viscoelastic effects in circular edge waves. J. Fluid Mech. 919, A18.CrossRefGoogle Scholar
Shao, X., Wilson, P., Saylor, J.R. & Bostwick, J.B. 2021 b Surface wave pattern formation in a cylindrical container. J. Fluid Mech. 915, A19.CrossRefGoogle Scholar
Simonelli, F. & Gollub, J.P. 1989 Surface wave mode interactions: effects of symmetry and degeneracy. J. Fluid Mech. 199, 471–494.CrossRefGoogle Scholar
Strickland, S.L., Shearer, M. & Daniels, K.E. 2015 Spatiotemporal measurement of surfactant distribution on gravity–capillary waves. J. Fluid Mech. 777, 523–543.CrossRefGoogle Scholar
Takeda, M. & Mutoh, K. 1983 Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 22 (24), 3977–3982.CrossRefGoogle ScholarPubMed
Umeki, M. 1991 Faraday resonance in rectangular geometry. J. Fluid Mech. 227, 161–192.CrossRefGoogle Scholar
Wagner, C., Müller, H.W. & Knorr, K. 1999 Faraday waves on a viscoelastic liquid. Phys. Rev. Lett. 83 (2), 308.CrossRefGoogle Scholar
Westra, M.-T., Binks, D.J. & Van De Water, W. 2003 Patterns of Faraday waves. J. Fluid Mech. 496, 1–32.CrossRefGoogle Scholar
Wilson, P., Shao, X., Saylor, J.R. & Bostwick, J.B. 2022 Role of edge effects and fluid depth in azimuthal Faraday waves. Phys. Rev. Fluids 7 (1), 014803.CrossRefGoogle Scholar
Yang, J. & Bhattacharya, K. 2019 Augmented lagrangian digital image correlation. Exp. Mech. 59 (2), 187–205.CrossRefGoogle Scholar
Zhang, W. & Viñals, J. 1996 Square patterns and quasipatterns in weakly damped Faraday waves. Phys. Rev. E 53 (5), R4283.CrossRefGoogle ScholarPubMed
Zhang, W. & Viñals, J. 1997 Pattern formation in weakly damped parametric surface waves. J. Fluid Mech. 336, 301–330.CrossRefGoogle Scholar

Zhang et al. Supplementary Movie

2D view of reconstructed surface and fitting surface of the (3,3) mode.

Download Zhang et al. Supplementary Movie(Video)
Video 1.1 MB