Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-29T23:27:03.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Penetrative internally heated convection in two and three dimensions

Published online by Cambridge University Press:  24 February 2016

David Goluskin  and
Erwin P. van der Poel
David Goluskin*
Affiliation:
Mathematics Department and Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA
Erwin P. van der Poel
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J.M. Burgers Center for Fluid Dynamics and MESA+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: goluskin@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Convection of an internally heated fluid, confined between top and bottom plates of equal temperature, is studied by direct numerical simulation in two and three dimensions. The unstably stratified upper region drives convection that penetrates into the stably stratified lower region. The fraction of produced heat escaping across the bottom plate, which is one half without convection, initially decreases as convection strengthens. Entering the turbulent regime, this decrease reverses in two dimensions but continues monotonically in three dimensions. 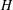The mean fluid temperature, which grows proportionally to the heating rate ( $H$ ) without convection, grows proportionally to 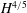$H^{4/5}$ when convection is strong in both two and three dimensions. The ratio of the heating rate to the fluid temperature is likened to the Nusselt number of Rayleigh–Bénard convection. Simulations are reported for Prandtl numbers between 0.1 and 10 and for Rayleigh numbers (defined in terms of the heating rate) up to 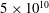$5\times 10^{10}$ .

JFM classification

Convection: Convection

Information

Type
Rapids
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , R6
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Asfia, F. J. & Dhir, V. K. 1996 An experimental study of natural convection in a volumetrically heated spherical pool bounded on top with a rigid wall. Nucl. Engng Des. 163 (3), 333–348.CrossRefGoogle Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Constantin, P. & Doering, C. R. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53 (6), 5957–5981.Google Scholar
Emara, A. A. & Kulacki, F. A. 1980 A numerical investigation of thermal convection in a heat-generating fluid layer. Trans. ASME J. Heat Transfer 102, 531–537.CrossRefGoogle Scholar
Fisher, P. F., Lottes, J. W. & Kerkemeier, S. G.2016, nek5000 Web page. http://nek5000.mcs.anl.gov.Google Scholar
Goluskin, D. 2015 Internally Heated Convection and Rayleigh–Bénard Convection. Springer.Google Scholar
Goluskin, D. & Spiegel, E. A. 2012 Convection driven by internal heating. Phys. Lett. A 377 (1–2), 83–92.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grötzbach, G. 1989 Turbulent heat transfer in an internally heated fluid layer. In Refined Flow Modelling and Turbulence Measurements (ed. Iwasa, Y., Tamai, N. & Wada, A.), pp. 267–275. Universal Academy.Google Scholar
Grötzbach, G. & Wörner, M. 1999 Direct numerical and large eddy simulations in nuclear applications. Intl J. Heat Fluid Flow 20 (3), 222–240.CrossRefGoogle Scholar
Hartlep, T., Tilgner, A. & Busse, F. H. 2005 Transition to turbulent convection in a fluid layer heated from below at moderate aspect ratio. J. Fluid Mech. 544, 309–322.Google Scholar
Irwin, P. 2009 Giant Planets of Our Solar System: Atmospheres, Composition, and Structure, 2nd edn. Springer.Google Scholar
Jahn, M. & Reineke, H. H. 1974 Free convection heat transfer with internal heat sources, calculations and measurements. In Proceedings of the 5th International Heat Transfer Conference, pp. 74–78.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 064501.CrossRefGoogle ScholarPubMed
Kippenhahn, R. & Weigert, A. 1994 Stellar Structure and Evolution. Springer.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5 (11), 1374–1389.CrossRefGoogle Scholar
Kulacki, F. A. & Goldstein, R. J. 1972 Thermal convection in a horizontal fluid layer with uniform volumetric energy sources. J. Fluid Mech. 55 (2), 271–287.Google Scholar
Lee, S. D., Lee, J. K. & Suh, K. Y. 2007 Boundary condition dependent natural convection in a rectangular pool with internal heat sources. Trans. ASME J. Heat Transfer 129 (5), 679–682.CrossRefGoogle Scholar
Lu, L., Doering, C. R. & Busse, F. H. 2004 Bounds on convection driven by internal heating. J. Math. Phys. 45 (7), 2967–2986.Google Scholar
Malkus, W. V. R. 1954 Discrete transitions in turbulent convection. Proc. R. Soc. Lond. A 225 (1161), 185–195.Google Scholar
Mayinger, F., Jahn, M., Reineke, H. H. & Steinberner, U.1975 Examination of thermohydraulic processes and heat transfer in a core melt. Tech. Rep. Hannover Technical University, Hannover, Germany.Google Scholar
Nourgaliev, R. R., Dinh, T. N. & Sehgal, B. R. 1997 Effect of fluid Prandtl number on heat transfer characteristics in internally heated liquid pools with Rayleigh numbers up to $10^{12}$ . Nucl. Engng Des. 169, 165–184.CrossRefGoogle Scholar
Orlandi, P. & Fatica, M. 1997 Direct simulations of turbulent flow in a pipe rotating about its axis. J. Fluid Mech. 343, 43–72.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.Google Scholar
Peale, S. J., Cassen, P. & Reynolds, R. T. 1979 Melting of Io by tidal dissipation. Science 203 (4383), 892–894.Google Scholar
Peckover, R. S. & Hutchinson, I. H. 1974 Convective rolls driven by internal heat sources. Phys. Fluids 17 (7), 1369–1371.CrossRefGoogle Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background field. J. Fluid Mech. 477, 363–379.CrossRefGoogle Scholar
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2013 Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.Google Scholar
Ralph, J. C., McGreevy, R. & Peckover, R. S. 1977 Experiments in tubulent thermal convection driven by internal heat sources. In Heat Transfer and Turbulent Buoyant Convection: Studies and Applications for Natural Environment, Buildings, Engineering Systems (ed. Spalding, D. B. & Afgan, N.), pp. 587–599. Hemisphere.Google Scholar
Rayleigh, Lord 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32 (192), 529–546.CrossRefGoogle Scholar
Schmalzl, J., Breuer, M. & Hansen, U. 2004 On the validity of two-dimensional numerical approaches to time-dependent thermal convection. Europhys. Lett. 67 (3), 390–396.Google Scholar
Schubert, G., Turcotte, D. L. & Olson, P. 2001 Mantle Convection in the Earth and Planets. Cambridge University Press.Google Scholar
Shen, Y. & Zikanov, O. 2015 Thermal convection in a liquid metal battery. Theor. Comput. Fluid Dyn. doi:10.1007/s00162-015-0378-1.Google Scholar
Sparrow, E. M., Goldstein, R. J. & Jonsson, V. K. 1964 Thermal instability in a horizontal fluid layer: effect of boundary conditions and non-linear temperature profile. J. Fluid Mech. 18, 513–528.Google Scholar
Spiegel, E. A. 1971 Turbulence in stellar convection zones. Comments Astrophys. Space Phys. 3 (2), 53–58.Google Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Straus, J. M. 1976 Penetrative convection in a layer of fluid heated from within. Astrophys. J. 209, 179–189.Google Scholar
Tveitereid, M. 1978 Thermal convection in a horizontal fluid layer with internal heat sources. Intl J. Heat Mass Transfer 21, 335–339.Google Scholar
Verzicco, R. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.Google Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
Wang, X. M. 2004 Infinite Prandtl number limit of Rayleigh–Bénard convection. Commun. Pure Appl. Maths 57, 1265–1285.Google Scholar
Wang, X. M. 2008 Stationary statistical properties of Rayleigh–Bénard convection at large Prandtl number. Commun. Pure Appl. Maths 61, 789–815.CrossRefGoogle Scholar
Wittenberg, R. W. 2010 Bounds on Rayleigh–Bénard convection with imperfectly conducting plates. J. Fluid Mech. 665, 158–198.Google Scholar
Wörner, M., Schmidt, M. & Grötzbach, G. 1997 Direct numerical simulation of turbulence in an internally heated convective fluid layer and implications for statistical modeling. J. Hydraul. Res. 35 (6), 773–797.Google Scholar

Goluskin et al. supplementary movie

Temperature field in a 3D simulation with Pr=1 and R=5×108. The coolest fluid is blue. Warmer fluid is orange, and the hottest fluid is transparent to aid visualization.

Download Goluskin et al. supplementary movie(Video)
Video 11.1 MB