Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
De Paoli, Marco
Alipour, Mobin
and
Soldati, Alfredo
2020.
How non-Darcy effects influence scaling laws in Hele-Shaw convection experiments.
Journal of Fluid Mechanics,
Vol. 892,
Issue. ,
Hewitt, D. R.
2020.
Vigorous convection in porous media.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 476,
Issue. 2239,
p.
20200111.
Alipour, Mobin
De Paoli, Marco
and
Soldati, Alfredo
2020.
Concentration-based velocity reconstruction in convective Hele–Shaw flows.
Experiments in Fluids,
Vol. 61,
Issue. 9,
Boulais, Etienne
and
Gervais, Thomas
2020.
Two-dimensional convection–diffusion in multipolar flows with applications in microfluidics and groundwater flow.
Physics of Fluids,
Vol. 32,
Issue. 12,
Letelier, Juvenal A.
O’Sullivan, John
Reich, Martin
Veloso, Eugenio
Sánchez-Alfaro, Pablo
Aravena, Diego
Muñoz, Mauricio
and
Morata, Diego
2021.
Reservoir architecture model and heat transfer modes in the El Tatio-La Torta geothermal system, Central Andes of northern Chile.
Geothermics,
Vol. 89,
Issue. ,
p.
101940.
López-Ríos, J.
Rueda-Gómez, Diego A.
and
Villamizar-Roa, Élder J.
2021.
A 2D Model for Heat Transport in a Hele–Shaw Geometry.
Journal of Mathematical Fluid Mechanics,
Vol. 23,
Issue. 4,
Qiang, Wei
Xie, Mingli
Liu, Zhikang
Wang, Yong
Cao, Hui
and
Zhou, Hanwen
2021.
Asymptotic behaviour of heat transfer in two-dimensional turbulent convection with high-porosity fluid-saturated media.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Gasow, Stefan
Kuznetsov, Andrey V.
Avila, Marc
and
Jin, Yan
2021.
A macroscopic two-length-scale model for natural convection in porous media driven by a species-concentration gradient.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
De Paoli, Marco
2021.
Influence of reservoir properties on the dynamics of a migrating current of carbon dioxide.
Physics of Fluids,
Vol. 33,
Issue. 1,
Pérez-Estay, N.
Molina-Piernas, E.
Roquer, T.
Aravena, D.
Araya Vargas, J.
Morata, D.
Arancibia, G.
Valdenegro, P.
García, K.
and
Elizalde, D.
2022.
Shallow anatomy of hydrothermal systems controlled by the Liquiñe-Ofqui Fault System and the Andean Transverse Faults: Geophysical imaging of fluid pathways and practical implications for geothermal exploration.
Geothermics,
Vol. 104,
Issue. ,
p.
102435.
Gasow, Stefan
Kuznetsov, Andrey V.
and
Jin, Yan
2022.
Prediction of pore-scale-property dependent natural convection in porous media at high Rayleigh numbers.
International Journal of Thermal Sciences,
Vol. 179,
Issue. ,
p.
107635.
Erfani, Hamidreza
Babaei, Masoud
Berg, Carl Fredrik
and
Niasar, Vahid
2022.
Scaling CO2 convection in confined aquifers: Effects of dispersion, permeability anisotropy and geochemistry.
Advances in Water Resources,
Vol. 164,
Issue. ,
p.
104191.
Ulloa, Hugo N.
and
Letelier, Juvenal A.
2022.
Energetics and mixing of thermally driven flows in Hele-Shaw cells.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
De Paoli, Marco
Perissutti, Diego
Marchioli, Cristian
and
Soldati, Alfredo
2022.
Experimental assessment of mixing layer scaling laws in Rayleigh-Taylor instability.
Physical Review Fluids,
Vol. 7,
Issue. 9,
Letelier, J.A.
Ulloa, H.N.
Leyrer, J.
and
Ortega, J.H.
2023.
Scaling CO2–brine mixing in permeable media via analogue models.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
Kashanj, Sina
and
Nobes, David S.
2023.
Application of 4D two-colour LIF to explore the temperature field of laterally confined turbulent Rayleigh–Bénard convection.
Experiments in Fluids,
Vol. 64,
Issue. 3,
Shahriar, Md Fahim
and
Khanal, Aaditya
2023.
Effect of Formation Heterogeneity on CO2 Dissolution in Subsurface Porous Media.
ACS Earth and Space Chemistry,
Vol. 7,
Issue. 10,
p.
2073.
Noto, Daisuke
Ulloa, Hugo N.
and
Letelier, Juvenal A.
2023.
Reconstructing temperature fields for thermally-driven flows under quasi-steady state.
Experiments in Fluids,
Vol. 64,
Issue. 4,
De Paoli, Marco
2023.
Convective mixing in porous media: a review of Darcy, pore-scale and Hele-Shaw studies.
The European Physical Journal E,
Vol. 46,
Issue. 12,
Zhu, Xiaojue
Fu, Yifeng
and
De Paoli, Marco
2024.
Transport scaling in porous media convection.
Journal of Fluid Mechanics,
Vol. 991,
Issue. ,
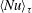 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and dimensionless mean thermal dissipation rate
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and dimensionless mean thermal dissipation rate 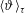 $\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ in the high-Rayleigh regime. We demonstrate that
$\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ in the high-Rayleigh regime. We demonstrate that 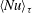 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and 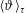 $\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ depend upon the cell anisotropy ratio
$\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ depend upon the cell anisotropy ratio  $\unicode[STIX]{x1D716}$, which measures the ratio between the cell gap and height. We show that
$\unicode[STIX]{x1D716}$, which measures the ratio between the cell gap and height. We show that 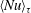 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ values in the high-Rayleigh regime decrease when
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ values in the high-Rayleigh regime decrease when  $\unicode[STIX]{x1D716}$ grows, supporting the field observations at the fracture scale. When
$\unicode[STIX]{x1D716}$ grows, supporting the field observations at the fracture scale. When 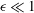 $\unicode[STIX]{x1D716}\ll 1$, our results are in agreement with the scalings found using the Darcy model. The numerical results satisfy the theoretical relation
$\unicode[STIX]{x1D716}\ll 1$, our results are in agreement with the scalings found using the Darcy model. The numerical results satisfy the theoretical relation 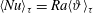 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}=Ra\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$, which is obtained from the model. This latter relation is valid for all values of Rayleigh number considered. The perturbative effects of cell aperture are observed only in the exponents of the scalings
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}=Ra\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$, which is obtained from the model. This latter relation is valid for all values of Rayleigh number considered. The perturbative effects of cell aperture are observed only in the exponents of the scalings 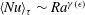 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})}$ and
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})}$ and 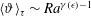 $\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})-1}$.
$\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})-1}$.