Hostname: page-component-65f69f4695-bj4tz Total loading time: 0 Render date: 2025-06-28T04:20:28.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Phoretic self-propulsion at finite Péclet numbers

Published online by Cambridge University Press:  23 April 2014

Sébastien Michelin  and
Eric Lauga
Sébastien Michelin*
Affiliation:
LadHyX, Département de Mécanique, Ecole Polytechnique – CNRS, 91128 Palaiseau, France
Eric Lauga
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: sebastien.michelin@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Phoretic self-propulsion is a unique example of force- and torque-free motion on small scales. The classical framework describing the flow field around a particle swimming by self-diffusiophoresis neglects the advection of the solute field by the flow and assumes that the chemical interaction layer is thin compared to the particle size. In this paper we quantify and characterize the effect of solute advection on the phoretic swimming of a sphere. 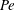We first rigorously derive the regime of validity of the thin-interaction-layer assumption at finite values of the Péclet number (${Pe}$). Under this assumption, we solve computationally the flow around Janus phoretic particles and examine the impact of solute advection on propulsion and the flow created by the particle. We demonstrate that although advection always leads to a decrease of the swimming speed and flow stresslet at high values of the Péclet number, an increase can be obtained at intermediate values of 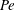${Pe}$. This possible enhancement of swimming depends critically on the nature of the chemical interactions between the solute and the surface. We then derive an asymptotic analysis of the problem at small 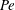${Pe}$ which allows us to rationalize our computational results. Our computational and theoretical analysis is accompanied by a parallel study of the influence of reactive effects at the surface of the particle (Damköhler number) on swimming.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Low-Reynolds-number flows: Low-Reynolds-number flows Biological Fluid Dynamics: Swimming/flying

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 572 - 604
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21, 61–99.CrossRefGoogle Scholar
Anderson, J. L. & Prieve, D. C. 1991 Diffusiophoresis caused by gradients of strongly adsorbing solutes. Langmuir 7, 403–406.CrossRefGoogle Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Bickel, T., Majee, A. & Würger, A. 2013 Flow pattern in the vicinity of self-propelling hot Janus particles. Phys. Rev. E 88, 012301.CrossRefGoogle ScholarPubMed
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46, 199–208.CrossRefGoogle Scholar
Brady, J. 2011 Particle motion driven by solute gradients with application to autonomous motion: continuum and colloidal perspectives. J. Fluid Mech. 667, 216–259.Google Scholar
Bray, D. 2000 Cell Movements: From Molecules to Motility. Garland Science.Google Scholar
Brennen, C. & Winnet, H. 1977 Fluid mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech. 9, 339–398.CrossRefGoogle Scholar
Broyden, C. G. 1965 A class of methods for solving nonlinear simultaneous equations. Maths Comput. 19, 577–593.CrossRefGoogle Scholar
Córdova-Figueroa, U. M. & Brady, J. F. 2008 Osmotic propulsion: the osmotic motor. Phys. Rev. Lett. 100 (15), 158303 ; see also the comment on this article by F. Jülicher & J. Prost, Phys. Rev. Lett. 103, 079801.CrossRefGoogle ScholarPubMed
Córdova-Figueroa, U. M., Brady, J. F. & Shklyaev, S. 2013 Osmotic propulsion of colloidal particles via constant surface flux. Soft Matt. 9, 6382–6390.Google Scholar
Dreyfus, R., Baudry, J., Roper, M. L., Fermigier, M., Stone, H. A. & Bibette, J. 2005 Microscopic artificial swimmers. Nature 437, 862–865.CrossRefGoogle ScholarPubMed
Ebbens, S. J. & Howse, J. R. 2011 Direct observation of the direction of motion for spherical catalytic swimmers. Langmuir 27, 12293–12296.Google Scholar
Ebbens, S., Tu, M.-H., Howse, J. R. & Golestanian, R. 2012 Size dependence of the propulsion velocity for catalytic Janus-sphere swimmers. Phys. Rev. E 85, 020401.Google Scholar
Gao, W., Sattayasamitsathit, S., Manesh, K. M., Weihs, D. & Wang, J. 2010 Magnetically powered flexible metal nanowire motors. J. Am. Chem. Soc. 132, 14403–14405.Google Scholar
Ghosh, A. & Fischer, P. 2009 Controlled propulsion of artificial magnetic nanostructured propellers. Nano Lett. 9, 2243–2245.CrossRefGoogle ScholarPubMed
Golestanian, R., Liverpool, T. B. & Ajdari, A. 2005 Propulsion of a molecular machine by asymmetric distribution of reaction products. Phys. Rev. Lett. 94 (22), 220801.Google Scholar
Golestanian, R., Liverpool, T. B. & Ajdari, A. 2007 Designing phoretic micro- and nano-swimmers. New J. Phys. 9, 126.Google Scholar
Howse, J. R., Jones, R. A. L., Ryan, A. J., Gough, T., Vafabakhsh, R. & Golestanian, R. 2007 Self-motile colloidal particles: from directed propulsion to random walk. Phys. Rev. Lett. 99, 048102.CrossRefGoogle ScholarPubMed
Jiang, H.-R., Yoshinaga, N. & Sano, M. 2010 Active motion of a Janus particle by self-thermophoresis in a defocused laser beam. Phys. Rev. Lett. 105, 268302.Google Scholar
Jülicher, F. & Prost, J. 2009a Comment on osmotic propulsion: the osmotic motor. Phys. Rev. Lett. 103, 079801.CrossRefGoogle ScholarPubMed
Jülicher, F. & Prost, J. 2009b Generic theory of colloidal transport. Eur. Phys. J. E 29 (1), 27–36.CrossRefGoogle ScholarPubMed
Khair, A. S. 2013 Diffusiophoresis of colloidal particles in neutral solute gradients at finite Péclet number. J. Fluid Mech. 731, 64–94.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming micro-organisms. Rep. Prog. Phys. 72, 096601.CrossRefGoogle Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56, 65–91.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23 (10), 101901.Google Scholar
Michelin, S. & Lauga, E. 2013 Unsteady feeding and optimal strokes of model ciliates. J. Fluid Mech. 715, 1–31.Google Scholar
Michelin, S., Lauga, E. & Bartolo, D. 2013 Spontaneous autophoretic motion of isotropic particles. Phys. Fluids 25, 061701.Google Scholar
Nelson, B. J., Kaliakatsos, I. K. & Abbott, J. J. 2010 Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Engng 12 (1), 55–85.CrossRefGoogle ScholarPubMed
O’Brien, R. W. 1983 The solution of the electrokinetic equations for colloidal particles with thin double layers. J. Colloid Interface Sci. 92, 204–216.Google Scholar
Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J. & Chaikin, P. M. 2013 Living crystals of light-activated colloidal surfers. Science 339, 936–940.Google Scholar
Paxton, W. F., Kistler, K. C., Olmeda, C. C., Sen, A., Angelo, S. K. St., Cao, Y., Mallouk, T. E., Lammert, P. E. & Crespi, V. H. 2004 Catalytic nanomotors: autonomous movement of striped nanorods. J. Am. Chem. Soc. 126 (41), 13424–13431.CrossRefGoogle ScholarPubMed
Popescu, M. N., Dietrich, S., Tasinkevych, M. & Ralston, J. 2010 Phoretic motion of spheroidal particles due to self-generated solute gradients. Eur. Phys J. E 31, 351–367.Google Scholar
Prieve, D. C., Anderson, J. L., Ebel, J. P. & Lowell, M. E. 1984 Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 148, 247–269.CrossRefGoogle Scholar
Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys. 45, 3–11.Google Scholar
Sabass, B. & Seifert, U. 2012 Dynamics and efficiency of a self-propelled, diffusiophoretic swimmer. J. Chem. Phys. 136, 064508.CrossRefGoogle ScholarPubMed
Schmitt, M. & Stark, H. 2013 Swimming active droplet: a theoretical analysis. Eur. Phys. Lett. 101, 44008.Google Scholar
Sharifi-Mood, N., Koplik, J. & Maldarelli, C. 2013 Diffusiophoretic self-propulsion of colloids driven by a surface reaction: the sub-micron particle regime for exponential and van der Waals interactions. Phys. Fluids 25, 012001.Google Scholar
Stone, H. A. & Samuel, A. D. T. 1996 Propulsion of microorganisms by surface distorsions. Phys. Rev. Lett. 77, 4102.Google Scholar
Theurkauff, I., Cottin-Bizonne, C., Palacci, J., Ybert, C. & Bocquet, L. 2012 Dynamic clustering in active colloidal suspensions with chemical signaling. Phys. Rev. Lett. 108, 268303.Google Scholar
Thutupalli, S., Seemann, R. & Herminghaus, S. 2011 Swarming behaviour of simple model squirmers. New J. Phys. 13, 073021.CrossRefGoogle Scholar
Walther, A. & Müller, A. H. E. 2008 Janus particles. Soft Matt. 4, 663–668.Google Scholar
Wang, J. 2009 Can man-made nanomachines compete with nature biomotors?. ACS Nano 3, 4–9.Google Scholar
Yariv, E. 2010 An asymptotic derivation of the thin-Debye-layer limit for electrokinetic phenomena. Chem. Engng Commun. 197, 3–17.Google Scholar
Yoshinaga, N., Nagai, K. H., Sumino, Y. & Kitahata, H. 2012 Drift instability in the motion of a fluid droplet with a chemically reactive surface driven by Marangoni flow. Phys. Rev. E 86, 016108.CrossRefGoogle ScholarPubMed
Zhang, L., Peyer, K. E. & Nelson, B. J. 2010 Artificial bacterial flagella for micromanipulation. Lab on a Chip 10, 2203–2215.Google Scholar