Article contents
Phoretic self-propulsion at large Péclet numbers
Published online by Cambridge University Press: 27 February 2015
Abstract
We analyse the self-diffusiophoresis of a spherical particle animated by a non-uniform chemical reaction at its boundary. We consider two models of solute absorption, one with a specified distribution of interfacial solute flux and one where this flux is governed by first-order kinetics with a specified distribution of rate constant. We employ a macroscale model where the short-range interaction of the solute with the particle boundary is represented by an effective slip condition. The solute transport is governed by an advection–diffusion equation. We focus upon the singular limit of large Péclet numbers, 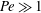 $\mathit{Pe}\gg 1$ . In the fixed-flux model, the excess-solute concentration is confined to a narrow boundary layer. The scaling pertinent to that limit allows the problem governing the solute concentration to be decoupled from the flow field. The resulting nonlinear boundary-layer problem is handled using a transformation to stream-function coordinates and a subsequent application of Fourier transforms, and is thereby reduced to a nonlinear integral equation governing the interfacial concentration. Its solution provides the requisite approximation for the particle velocity, which scales as
$\mathit{Pe}\gg 1$ . In the fixed-flux model, the excess-solute concentration is confined to a narrow boundary layer. The scaling pertinent to that limit allows the problem governing the solute concentration to be decoupled from the flow field. The resulting nonlinear boundary-layer problem is handled using a transformation to stream-function coordinates and a subsequent application of Fourier transforms, and is thereby reduced to a nonlinear integral equation governing the interfacial concentration. Its solution provides the requisite approximation for the particle velocity, which scales as 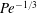 $\mathit{Pe}^{-1/3}$ . In the fixed-rate model, large Péclet numbers may be realized in different limit processes. We consider the case of large swimmers or strong reaction, where the Damköhler number
$\mathit{Pe}^{-1/3}$ . In the fixed-rate model, large Péclet numbers may be realized in different limit processes. We consider the case of large swimmers or strong reaction, where the Damköhler number 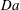 $\mathit{Da}$ is large as well, scaling as
$\mathit{Da}$ is large as well, scaling as 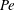 $\mathit{Pe}$ . In that double limit, where no boundary layer is formed, we obtain a closed-form approximation for the particle velocity, expressed as a nonlinear functional of the rate-constant distribution; this velocity scales as
$\mathit{Pe}$ . In that double limit, where no boundary layer is formed, we obtain a closed-form approximation for the particle velocity, expressed as a nonlinear functional of the rate-constant distribution; this velocity scales as 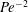 $\mathit{Pe}^{-2}$ . Both the fixed-flux and fixed-rate asymptotic predictions agree with the numerical values provided by computational solutions of the nonlinear transport problem.
$\mathit{Pe}^{-2}$ . Both the fixed-flux and fixed-rate asymptotic predictions agree with the numerical values provided by computational solutions of the nonlinear transport problem.
JFM classification
Information
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 24
- Cited by


