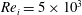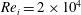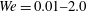1 Introduction
Drag in turbulent flows is a major drain of energy. It is well known that the addition of a secondary phase such as polymers or bubbles into a turbulent carrier fluid can lead to significant reduction in the overall drag in the system (van den Berg et al.
Reference van den Berg, Luther, Lathrop and Lohse2005; White & Mungal Reference White and Mungal2008; Ceccio Reference Ceccio2010; van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016). Here, we define drag reduction (
![]() $DR$
) as
$DR$
) as
where
![]() $C_{f,0}$
and
$C_{f,0}$
and
![]() $C_{f,\unicode[STIX]{x1D6FC}}$
are the friction coefficients with
$C_{f,\unicode[STIX]{x1D6FC}}$
are the friction coefficients with
![]() $\unicode[STIX]{x1D6FC}$
the volume fraction of the secondary phase injected into the system. For example, a small volume fraction of bubbles (
$\unicode[STIX]{x1D6FC}$
the volume fraction of the secondary phase injected into the system. For example, a small volume fraction of bubbles (
![]() ${<}$
4 %) injected into a turbulent carrier liquid can reduce the overall drag of the system by up to 40 % (van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016). The extent of modification in momentum transport that can be achieved through bubble injection makes the phenomena relevant for both fundamental studies of multiphase flows and large-scale industrial applications (Ceccio Reference Ceccio2010). However, given the many challenges and large number of control parameters in theoretical, experimental and numerical techniques, the governing physics in multiphase flows is not fully understood. The key parameters that play a role in the overall drag reduction measured in a multiphase turbulent system are the Reynolds number of the carrier fluid, the geometry of the flow, the relative size of the dispersed phase in comparison to the Kolmogorov scale (either sub-Kolmogorov or finite size), gravity, volume fraction and surface tension of the dispersed phase. In this paper, we use direct numerical simulations (DNS) to uncover the effect of deformability of finite-size bubbles on the overall drag in a canonical wall-bounded shear-driven system, namely in Taylor–Couette (TC) flow.
${<}$
4 %) injected into a turbulent carrier liquid can reduce the overall drag of the system by up to 40 % (van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al.
Reference Verschoof, van der Veen, Sun and Lohse2016). The extent of modification in momentum transport that can be achieved through bubble injection makes the phenomena relevant for both fundamental studies of multiphase flows and large-scale industrial applications (Ceccio Reference Ceccio2010). However, given the many challenges and large number of control parameters in theoretical, experimental and numerical techniques, the governing physics in multiphase flows is not fully understood. The key parameters that play a role in the overall drag reduction measured in a multiphase turbulent system are the Reynolds number of the carrier fluid, the geometry of the flow, the relative size of the dispersed phase in comparison to the Kolmogorov scale (either sub-Kolmogorov or finite size), gravity, volume fraction and surface tension of the dispersed phase. In this paper, we use direct numerical simulations (DNS) to uncover the effect of deformability of finite-size bubbles on the overall drag in a canonical wall-bounded shear-driven system, namely in Taylor–Couette (TC) flow.
In TC flow, the fluid is driven by two independently rotating co-axial cylinders. It has been one of the classical systems to study shear-driven fluid dynamics for the past several decades (see Grossmann, Lohse & Sun (Reference Grossmann, Lohse and Sun2016) for a recent review). The geometry of TC flow is closed, simple and allows for exact global balance relations between the driving and dissipation in the flow, which opens up the possibility for high-precision experiments and numerical simulations. In the context of multiphase TC flow, experimental and numerical studies have demonstrated that the overall drag in the system can be reduced with the injection of a small volume fraction of bubbles (Murai, Oiwa & Takeda Reference Murai, Oiwa and Takeda2005, Reference Murai, Oiwa and Takeda2008; Sugiyama, Calzavarini & Lohse Reference Sugiyama, Calzavarini and Lohse2008; Spandan et al. Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016). Given the simple and closed nature of TC flow, in comparison to other canonical systems, multiphase TC flow is an ideal playground to understand the governing physics behind bubble-induced drag reduction. In contrast, studies on bubble-induced drag reduction in classical plane channel flows suffer from limitations in the domain size in the streamwise direction. TC flow on the other hand is naturally limited in the streamwise (azimuthal) direction, thus minimising any domain-size effects.
Various mechanisms have been proposed to explain the origin of the bubble-induced drag reduction effect (Ferrante & Elghobashi Reference Ferrante and Elghobashi2004; Lu, Fernández & Tryggvason Reference Lu, Fernández and Tryggvason2005; L’vov et al. Reference L’vov, Pomyalov, Procaccia and Tiberkevich2005; van den Berg et al. Reference van den Berg, van Gils, Lathrop and Lohse2007; Lu & Tryggvason Reference Lu and Tryggvason2008; Sugiyama et al. Reference Sugiyama, Calzavarini and Lohse2008; Ceccio Reference Ceccio2010; van Gils et al. Reference van Gils, Narezo Guzman, Sun and Lohse2013; Spandan et al. Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016; Verschoof et al. Reference Verschoof, van der Veen, Sun and Lohse2016; Spandan, Verzicco & Lohse Reference Spandan, Verzicco and Lohse2017b ). When the carrier fluid is weakly turbulent (laminar boundary layers and turbulent bulk), the effective buoyancy of dispersed sub-Kolmogorov bubbles, which is described by the Froude number, plays an important role in governing drag reduction in the system (Spandan et al. Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016). When the carrier fluid becomes highly turbulent (both boundary layer and bulk are turbulent), the buoyancy of sub-Kolmogorov bubbles is no longer sufficient to achieve strong drag reduction effects. Numerical simulations have shown that in the highly turbulent regime, even deformability of sub-Kolmogorov bubbles does not contribute to drag reduction (Spandan et al. Reference Spandan, Verzicco and Lohse2017b ). In the highly turbulent regime, deformability of finite-size (larger than the Kolmogorov scale) bubbles seems to be a promising mechanism to achieve strong drag reduction (van Gils et al. Reference van Gils, Narezo Guzman, Sun and Lohse2013; Verschoof et al. Reference Verschoof, van der Veen, Sun and Lohse2016). However, it is unclear why the extent of deformability of finite-size bubbles is important for achieving strong drag reduction in highly turbulent TC flow.
In this paper, we show that the origin of deformability-induced drag reduction is linked to reduced dissipation in the wake of finite-size (larger than the Kolmogorov scale) deformable bubbles in comparison to rigid spherical bubbles. Using fully resolved numerical simulations we are able to identify and separate the various effects contributing to drag reduction in the flow, and furthermore look at the individual contributions from these effects. We find that the reduced dissipation in the bubble wake is the dominant mechanism of drag reduction, irrespective of whether the carrier fluid is weakly or highly turbulent.
2 Numerical details and parameters
The dynamics of the carrier phase is solved using DNS of the Navier–Stokes equations in cylindrical coordinates. The governing equations for the carrier phase are
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $p$
are the carrier phase velocity and pressure, respectively, while
$p$
are the carrier phase velocity and pressure, respectively, while
![]() $\boldsymbol{f}_{b}(\boldsymbol{x},t)$
is a source term included in the fluid momentum equation arising from the immersed boundary method (IBM) and is used to enforce the interfacial boundary condition at the bubble–fluid interface. A second-order-accurate finite-difference scheme with fractional time stepping is used for the spatial and temporal discretisation of equations (2.1) and (2.2) (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015). Unlike sub-Kolmogorov bubbles which can be modelled using the point-particle approximation (Elghobashi Reference Elghobashi1994), finite-size bubbles which are much bigger than the Kolmogorov scale experience non-uniform flow conditions on the surface. In such a case, momentum exchange between the carrier fluid and dispersed bubbles cannot be modelled using pointwise approximations, but has to be fully resolved. This is done using IBM where each dispersed bubble is discretised using an unstructured Lagrangian mesh which resides over a structured Eulerian mesh on which equations (2.1) and (2.2) are solved. The influence of the dispersed bubbles on the carrier fluid is accounted for through a volume-averaged force first computed on the Lagrangian mesh and then transferred to the Eulerian mesh in a conservative manner. A no-slip boundary condition is imposed on the interface of each bubble which physically corresponds to a contaminated interface. While the IBM also allows for imposing a free-slip boundary condition which replicates a free-slip interface, we restrict ourselves to contaminated interfaces in this work as it can be handled easily from a numerical point of view. Due to the lack of a boundary layer along the surface of clean bubbles with a free-slip interface, it can be expected that the resulting local dissipation is lower in comparison to contaminated no-slip bubbles. This may lead to an increase in the magnitude of drag reduction in comparison to contaminated no-slip bubbles. In this study, we focus on understanding the physical mechanisms relevant for increasing drag reduction with increasing deformability of contaminated no-slip finite-size bubbles.
$\boldsymbol{f}_{b}(\boldsymbol{x},t)$
is a source term included in the fluid momentum equation arising from the immersed boundary method (IBM) and is used to enforce the interfacial boundary condition at the bubble–fluid interface. A second-order-accurate finite-difference scheme with fractional time stepping is used for the spatial and temporal discretisation of equations (2.1) and (2.2) (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al.
Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015). Unlike sub-Kolmogorov bubbles which can be modelled using the point-particle approximation (Elghobashi Reference Elghobashi1994), finite-size bubbles which are much bigger than the Kolmogorov scale experience non-uniform flow conditions on the surface. In such a case, momentum exchange between the carrier fluid and dispersed bubbles cannot be modelled using pointwise approximations, but has to be fully resolved. This is done using IBM where each dispersed bubble is discretised using an unstructured Lagrangian mesh which resides over a structured Eulerian mesh on which equations (2.1) and (2.2) are solved. The influence of the dispersed bubbles on the carrier fluid is accounted for through a volume-averaged force first computed on the Lagrangian mesh and then transferred to the Eulerian mesh in a conservative manner. A no-slip boundary condition is imposed on the interface of each bubble which physically corresponds to a contaminated interface. While the IBM also allows for imposing a free-slip boundary condition which replicates a free-slip interface, we restrict ourselves to contaminated interfaces in this work as it can be handled easily from a numerical point of view. Due to the lack of a boundary layer along the surface of clean bubbles with a free-slip interface, it can be expected that the resulting local dissipation is lower in comparison to contaminated no-slip bubbles. This may lead to an increase in the magnitude of drag reduction in comparison to contaminated no-slip bubbles. In this study, we focus on understanding the physical mechanisms relevant for increasing drag reduction with increasing deformability of contaminated no-slip finite-size bubbles.
The deformation dynamics of the immersed bubbles is computed through an interaction potential (IP) approach where the characteristic surface tension of a liquid–liquid interface is replicated using a triangulated network of in-plane elastic and out-of-plane torsional springs. The IP approach for modelling deformation of immersed liquid–liquid interfaces has proved to be reliable and self-consistent as long as the immersed interfaces do not approach their breakup limit. The basic idea behind the IP approach is that under the action of external forces, the immersed interface adjusts itself through the action of internal spring forces such that the total displacement potential energy tends to a minimum. All bubbles are initialised with a spherical triangulated network of springs. While external forces such as local pressure fluctuations and viscous stresses deform the surface, the internal spring forces tends to bring the deformed surface back to its initial spherical shape with a goal to minimise the overall potential energy stored in the network. Given the finite-size nature of the immersed bubbles, the pressure fluctuations and viscous stresses are computed locally on individual triangular elements (Spandan et al. Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a ). The elastic constants required to model the triangulated network in the IP approach for interfaces is chosen through a tuning procedure. The tuning of the surface properties of the triangulated network and its corresponding Weber number (defined later) is performed for a centroid fixed bubble in a cross-flow, as described in Spandan et al. (Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a ). Here, it is important to note that the IP model is not an exact representation of the surface tension phenomenon and it is to be taken as a phenomenological approach to mimic the deformation characteristic of immersed drops or bubbles. Additional details on the IBM, the interaction potential approach and the parallelisation schemes can be found in de Tullio & Pascazio (Reference de Tullio and Pascazio2016) and Spandan et al. (Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a ).
The geometrical control parameters in TC flow are the radius ratio
![]() $\unicode[STIX]{x1D702}=r_{i}/r_{o}$
and the aspect ratio
$\unicode[STIX]{x1D702}=r_{i}/r_{o}$
and the aspect ratio
![]() $\unicode[STIX]{x1D6E4}=L/(r_{o}-r_{i})$
, where
$\unicode[STIX]{x1D6E4}=L/(r_{o}-r_{i})$
, where
![]() $r_{i}$
,
$r_{i}$
,
![]() $r_{o}$
are the radii of the inner cylinder (IC) and outer cylinder (OC), respectively, and
$r_{o}$
are the radii of the inner cylinder (IC) and outer cylinder (OC), respectively, and
![]() $L$
is the height of the cylinders. In this paper, we set
$L$
is the height of the cylinders. In this paper, we set
![]() $\unicode[STIX]{x1D702}=0.909$
and
$\unicode[STIX]{x1D702}=0.909$
and
![]() $\unicode[STIX]{x1D6E4}=2.0$
. The driving in the system is characterised by the IC Reynolds number
$\unicode[STIX]{x1D6E4}=2.0$
. The driving in the system is characterised by the IC Reynolds number
![]() $Re_{i}=Ud/\unicode[STIX]{x1D708}$
, where
$Re_{i}=Ud/\unicode[STIX]{x1D708}$
, where
![]() $U$
is the velocity of the IC,
$U$
is the velocity of the IC,
![]() $d=r_{o}-r_{i}$
is the gap width between the cylinders and
$d=r_{o}-r_{i}$
is the gap width between the cylinders and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity of the carrier fluid; the OC is kept stationary. In the following section, we study the effect of finite-size deformable bubbles on the carrier fluid dynamics for two different IC Reynolds numbers i.e.
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the carrier fluid; the OC is kept stationary. In the following section, we study the effect of finite-size deformable bubbles on the carrier fluid dynamics for two different IC Reynolds numbers i.e.
![]() $Re_{i}=5\times 10^{3}$
and
$Re_{i}=5\times 10^{3}$
and
![]() $Re_{i}=2\times 10^{4}$
, which are hereafter referred to as low- and high-
$Re_{i}=2\times 10^{4}$
, which are hereafter referred to as low- and high-
![]() $Re_{i}$
cases, respectively. The extent of deformability of the immersed bubbles is controlled through the Weber number
$Re_{i}$
cases, respectively. The extent of deformability of the immersed bubbles is controlled through the Weber number
![]() $We=\unicode[STIX]{x1D70C}_{f}U^{2}d_{p}/\unicode[STIX]{x1D70E}$
, where
$We=\unicode[STIX]{x1D70C}_{f}U^{2}d_{p}/\unicode[STIX]{x1D70E}$
, where
![]() $\unicode[STIX]{x1D70C}_{f}$
,
$\unicode[STIX]{x1D70C}_{f}$
,
![]() $d_{p}$
and
$d_{p}$
and
![]() $\unicode[STIX]{x1D70E}$
are the fluid density, bubble diameter and surface tension, respectively. The Weber number of the bubbles considered are
$\unicode[STIX]{x1D70E}$
are the fluid density, bubble diameter and surface tension, respectively. The Weber number of the bubbles considered are
![]() $We=10^{-2},0.5,1.0,2.0$
. In order to simulate rigid non-deformable bubbles (
$We=10^{-2},0.5,1.0,2.0$
. In order to simulate rigid non-deformable bubbles (
![]() $We=10^{-2}$
), numerical stiffness is avoided by treating the immersed bubbles as rigid spheres rather than compute the small-scale deformations from the IP model. The non-dimensional in-plane elastic constants for
$We=10^{-2}$
), numerical stiffness is avoided by treating the immersed bubbles as rigid spheres rather than compute the small-scale deformations from the IP model. The non-dimensional in-plane elastic constants for
![]() $We=0.5,1.0,2.0$
are
$We=0.5,1.0,2.0$
are
![]() $k_{e}^{\ast }=12.0\times 10^{-3},8\times 10^{-3},5\times 10^{-3}$
, respectively. The remaining constants used for the triangulated network are scaled according to the guidelines specified in Spandan et al. (Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a
); i.e. bending constant
$k_{e}^{\ast }=12.0\times 10^{-3},8\times 10^{-3},5\times 10^{-3}$
, respectively. The remaining constants used for the triangulated network are scaled according to the guidelines specified in Spandan et al. (Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a
); i.e. bending constant
![]() $k_{b}^{\ast }=k_{e}/10.0$
, volume constant
$k_{b}^{\ast }=k_{e}/10.0$
, volume constant
![]() $k_{v}^{\ast }\sim 10^{5}k_{e}^{\ast }$
and area constant
$k_{v}^{\ast }\sim 10^{5}k_{e}^{\ast }$
and area constant
![]() $k_{a}^{\ast }=k_{e}^{\ast }$
. The ratio of the mean edge length on the initial triangulated sphere to the gap width between the cylinders is approximately
$k_{a}^{\ast }=k_{e}^{\ast }$
. The ratio of the mean edge length on the initial triangulated sphere to the gap width between the cylinders is approximately
![]() $7.5\times 10^{-3}$
.
$7.5\times 10^{-3}$
.
In this paper, the main focus is to understand the effect of the Weber number
![]() $We$
, which quantifies the ratio between inertial and surface tension forces acting on the immersed bubbles. The choice of the reference velocity in the definition of
$We$
, which quantifies the ratio between inertial and surface tension forces acting on the immersed bubbles. The choice of the reference velocity in the definition of
![]() $We$
varies from one study to another; regardless of the definitions in simulations and experiments, the main idea is that the Weber number indicates the extent of deformability of the dispersed phase. We only consider bubbles which do not break up or coalesce in the flow; modelling the breakup and coalescence dynamics of bubbles in a turbulent environment is an extremely challenging task from both a physical and numerical point of view, and is not in the scope of this study. Collisions among the immersed bubbles and of the bubbles with the cylinder walls are implemented through an elastic potential between the Lagrangian markers and the centre of the Eulerian cell in which the Lagrangian marker resides. The numerical algorithm is as follows. At every time step, when two or more Lagrangian markers from different bubbles reside in the same Eulerian cell, all the Lagrangian markers in that Eulerian cell face a repulsive force proportional to the square of the inverse distance between the marker and the centre of the Eulerian cell. This ensures that different bubbles never come into contact with each other, thus avoiding any ‘ghost’ overlap between the Lagrangian meshes (Spandan et al.
Reference Spandan, Lohse, de Tullio and Verzicco2018). In the following simulations, in addition to ensuring energy conservation, we keep the same formulation of the collision elastic potential in all cases to eliminate any numerical artefacts among the different cases. The grid resolution for the carrier fluid is set to
$We$
varies from one study to another; regardless of the definitions in simulations and experiments, the main idea is that the Weber number indicates the extent of deformability of the dispersed phase. We only consider bubbles which do not break up or coalesce in the flow; modelling the breakup and coalescence dynamics of bubbles in a turbulent environment is an extremely challenging task from both a physical and numerical point of view, and is not in the scope of this study. Collisions among the immersed bubbles and of the bubbles with the cylinder walls are implemented through an elastic potential between the Lagrangian markers and the centre of the Eulerian cell in which the Lagrangian marker resides. The numerical algorithm is as follows. At every time step, when two or more Lagrangian markers from different bubbles reside in the same Eulerian cell, all the Lagrangian markers in that Eulerian cell face a repulsive force proportional to the square of the inverse distance between the marker and the centre of the Eulerian cell. This ensures that different bubbles never come into contact with each other, thus avoiding any ‘ghost’ overlap between the Lagrangian meshes (Spandan et al.
Reference Spandan, Lohse, de Tullio and Verzicco2018). In the following simulations, in addition to ensuring energy conservation, we keep the same formulation of the collision elastic potential in all cases to eliminate any numerical artefacts among the different cases. The grid resolution for the carrier fluid is set to
![]() $N_{\unicode[STIX]{x1D703}}\times N_{r}\times N_{z}=768\times 192\times 384$
and
$N_{\unicode[STIX]{x1D703}}\times N_{r}\times N_{z}=768\times 192\times 384$
and
![]() $N_{\unicode[STIX]{x1D703}}\times N_{r}\times N_{z}=1536\times 384\times 768$
for the low- and high-
$N_{\unicode[STIX]{x1D703}}\times N_{r}\times N_{z}=1536\times 384\times 768$
for the low- and high-
![]() $Re_{i}$
cases, respectively.
$Re_{i}$
cases, respectively.
A total of 120 bubbles are simulated along with a turbulent carrier fluid which corresponds to a global volume fraction of 0.1 %; each individual bubble is discretised using 1280 and 2560 Lagrangian markers for the low- and high-
![]() $Re_{i}$
cases, respectively. The density ratio of the bubbles to that of the carrier fluid is taken to be approximately
$Re_{i}$
cases, respectively. The density ratio of the bubbles to that of the carrier fluid is taken to be approximately
![]() $\tilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{b}/\unicode[STIX]{x1D70C}_{f}=0.05$
, which is larger than real gas bubbles but easier to handle numerically. The effective Froude number of the bubbles in all the simulations is kept the same and is defined as
$\tilde{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{b}/\unicode[STIX]{x1D70C}_{f}=0.05$
, which is larger than real gas bubbles but easier to handle numerically. The effective Froude number of the bubbles in all the simulations is kept the same and is defined as
![]() $Fr=\sqrt{\tilde{\unicode[STIX]{x1D70C}}U^{2}/((\tilde{\unicode[STIX]{x1D70C}}-1)gr_{i})}=0.64$
. For the IBM, we assume that the viscous force acting on the interface from the fluid entrapped inside the immersed ‘bubble’ is close to negligible; in the context of the IBM, this would correspond to a ratio of bubble-gas viscosity and carrier fluid to be approximately zero. To achieve numerical convergence, we run our simulations in a series of three steps. First, we allow the single-phase system to converge. We then initialise rigid bubbles and allow them to develop in the flow. Next, we allow them to deform corresponding to their imposed Weber number and run the simulation until the two-phase system has the developed statistical stationarity. The convergence criteria is described later. Since we keep the relative diameter (
$Fr=\sqrt{\tilde{\unicode[STIX]{x1D70C}}U^{2}/((\tilde{\unicode[STIX]{x1D70C}}-1)gr_{i})}=0.64$
. For the IBM, we assume that the viscous force acting on the interface from the fluid entrapped inside the immersed ‘bubble’ is close to negligible; in the context of the IBM, this would correspond to a ratio of bubble-gas viscosity and carrier fluid to be approximately zero. To achieve numerical convergence, we run our simulations in a series of three steps. First, we allow the single-phase system to converge. We then initialise rigid bubbles and allow them to develop in the flow. Next, we allow them to deform corresponding to their imposed Weber number and run the simulation until the two-phase system has the developed statistical stationarity. The convergence criteria is described later. Since we keep the relative diameter (
![]() $d_{p}$
) of the bubbles with respect to the gap width between the cylinders the same for both the low- and high-
$d_{p}$
) of the bubbles with respect to the gap width between the cylinders the same for both the low- and high-
![]() $Re_{i}$
cases (
$Re_{i}$
cases (
![]() $d_{b}/(r_{o}-r_{i})=0.1$
), the relative size of the bubbles in comparison to the Kolmogorov scale (
$d_{b}/(r_{o}-r_{i})=0.1$
), the relative size of the bubbles in comparison to the Kolmogorov scale (
![]() $\unicode[STIX]{x1D702}_{K}$
) of the corresponding single-phase flow is approximately
$\unicode[STIX]{x1D702}_{K}$
) of the corresponding single-phase flow is approximately
![]() $d_{p}/\unicode[STIX]{x1D702}_{K}\sim 14$
and
$d_{p}/\unicode[STIX]{x1D702}_{K}\sim 14$
and
![]() $d_{p}/\unicode[STIX]{x1D702}_{K}\sim 25$
for the low- and high-
$d_{p}/\unicode[STIX]{x1D702}_{K}\sim 25$
for the low- and high-
![]() $Re_{i}$
case, respectively.
$Re_{i}$
case, respectively.
3 Results
We now present results on the influence of the immersed bubbles on the carrier flow dynamics. The net percentage of drag reduction in a two-phase TC flow (here bubbles injected into carrier fluid) can be computed from the kinetic energy transport budget of the system as follows (see Appendix of Sugiyama et al. (Reference Sugiyama, Calzavarini and Lohse2008) for a detailed derivation):
Here
![]() $\langle \unicode[STIX]{x1D716}_{t}\rangle$
and
$\langle \unicode[STIX]{x1D716}_{t}\rangle$
and
![]() $\langle \unicode[STIX]{x1D716}_{s}\rangle$
are the mean kinetic energy dissipation rate per unit mass of the carrier fluid in the two-phase (with bubbles) and single-phase (without bubbles) cases, respectively;
$\langle \unicode[STIX]{x1D716}_{s}\rangle$
are the mean kinetic energy dissipation rate per unit mass of the carrier fluid in the two-phase (with bubbles) and single-phase (without bubbles) cases, respectively;
![]() $\boldsymbol{f}_{b}$
is the volume-averaged source term arising from the effect of the dispersed phase on the carrier fluid (cf. (2.1));
$\boldsymbol{f}_{b}$
is the volume-averaged source term arising from the effect of the dispersed phase on the carrier fluid (cf. (2.1));
![]() $\boldsymbol{u}$
is the local fluid velocity. A similar decomposition of the stresses transported in a multiphase channel flow is presented in Zhang & Prosperetti (Reference Zhang and Prosperetti2010). The two terms on the right-hand side of (3.1), which are named
$\boldsymbol{u}$
is the local fluid velocity. A similar decomposition of the stresses transported in a multiphase channel flow is presented in Zhang & Prosperetti (Reference Zhang and Prosperetti2010). The two terms on the right-hand side of (3.1), which are named
![]() $\langle DR\rangle _{1}$
and
$\langle DR\rangle _{1}$
and
![]() $\langle DR\rangle _{2}$
, correspond to different effects in the flow and the implications of this decomposition is discussed later. In figure 1(a), we plot the overall drag reduction
$\langle DR\rangle _{2}$
, correspond to different effects in the flow and the implications of this decomposition is discussed later. In figure 1(a), we plot the overall drag reduction
![]() $DR$
versus the Weber number (
$DR$
versus the Weber number (
![]() $We$
) of the bubbles injected into the flow for both low-
$We$
) of the bubbles injected into the flow for both low-
![]() $Re_{i}$
and high-
$Re_{i}$
and high-
![]() $Re_{i}$
cases. One can clearly observe an increasing trend in the drag reduction with increasing Weber number (i.e. increasing bubble deformability).
$Re_{i}$
cases. One can clearly observe an increasing trend in the drag reduction with increasing Weber number (i.e. increasing bubble deformability).

Figure 1. (a) Drag reduction (
![]() $DR$
) versus Weber (
$DR$
) versus Weber (
![]() $We$
) number. (b) Probability distribution function (PDF) of the radial (wall-normal) position of the centre of mass of individual bubbles. Since the bubbles are finite size and collide with the cylinders there is no data in the PDF very close to
$We$
) number. (b) Probability distribution function (PDF) of the radial (wall-normal) position of the centre of mass of individual bubbles. Since the bubbles are finite size and collide with the cylinders there is no data in the PDF very close to
![]() $\tilde{r}=0$
and
$\tilde{r}=0$
and
![]() $\tilde{r}=1$
, which correspond to the IC and OC, respectively.
$\tilde{r}=1$
, which correspond to the IC and OC, respectively.

Figure 2. Instantaneous snapshot of normalised dissipation
![]() $\hat{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}(U/d)^{2}$
in the mid-azimuthal and mid-axial planes for single-phase (a,c) and two-phase flow (b,d). (a,b)
$\hat{\unicode[STIX]{x1D716}}=\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}(U/d)^{2}$
in the mid-azimuthal and mid-axial planes for single-phase (a,c) and two-phase flow (b,d). (a,b)
![]() $Re_{i}=5\times 10^{3},We=1.0$
, (c,d)
$Re_{i}=5\times 10^{3},We=1.0$
, (c,d)
![]() $Re_{i}=2\times 10^{4},We=1.0$
. Dark colour indicates high dissipation and light colour indicates low dissipation. The dissipation in the bulk and near the OC is attenuated in the presence of bubbles (b,d) as compared to the single-phase flow (a,c).
$Re_{i}=2\times 10^{4},We=1.0$
. Dark colour indicates high dissipation and light colour indicates low dissipation. The dissipation in the bulk and near the OC is attenuated in the presence of bubbles (b,d) as compared to the single-phase flow (a,c).
Before analysing the trend in drag reduction with increasing Weber number, it is useful to understand the origin of drag reduction with buoyant bubbles. Similar to the effect seen in Spandan et al. (Reference Spandan, Ostilla-Mónico, Verzicco and Lohse2016), the buoyancy of bubbles causes a mean slip in the direction of the gravity (axial direction) and, in doing so, the bubbles weaken the plumes ejected from the inner cylinder, which are primarily wall-normal velocity fluctuations. The weakening of plumes occurs primarily through an axial (direction of buoyancy) perturbation of the wall-normal velocity fluctuations. By weakening the plumes, the bubbles also reduce the effective momentum transport from the inner cylinder to the outer cylinder, which consequently leads to drag reduction.
When the dispersed bubbles are sub-Kolmogorov, deformable bubbles prefer to accumulate near the IC, which enhances drag reduction because a higher concentration of bubbles near the IC is more effective in disrupting plume ejections (Spandan et al.
Reference Spandan, Verzicco and Lohse2017b
). In order to understand whether the increase in drag reduction with increasing deformability of finite-size bubbles has any correlation with local bubble accumulation near the IC, we plot the probability distribution function of the normalised radial position
![]() $\tilde{r}=(r-r_{i})/(r_{o}-r_{i})$
of the centre of mass of all bubbles in figure 1(b). In all cases, the bubbles prefer to position themselves near the IC due to centrifugal forces. However, in contrast to sub-Kolmogorov bubbles, we find no significant difference in the accumulation patterns of finite-size bubbles with increasing deformability. A possible explanation behind this distribution is that finite-size bubbles are less affected by small-scale flow structures (
$\tilde{r}=(r-r_{i})/(r_{o}-r_{i})$
of the centre of mass of all bubbles in figure 1(b). In all cases, the bubbles prefer to position themselves near the IC due to centrifugal forces. However, in contrast to sub-Kolmogorov bubbles, we find no significant difference in the accumulation patterns of finite-size bubbles with increasing deformability. A possible explanation behind this distribution is that finite-size bubbles are less affected by small-scale flow structures (
![]() $\unicode[STIX]{x1D702}_{K}$
to
$\unicode[STIX]{x1D702}_{K}$
to
![]() $5\unicode[STIX]{x1D702}_{K}$
) in comparison to sub-Kolmogorov bubbles. This suggests the presence of additional mechanisms which enhance drag reduction with increasing deformability in the case of finite-size bubbles.
$5\unicode[STIX]{x1D702}_{K}$
) in comparison to sub-Kolmogorov bubbles. This suggests the presence of additional mechanisms which enhance drag reduction with increasing deformability in the case of finite-size bubbles.
In order to show clearly the origin of drag reduction, in figure 2, we show pseudo-colour plots of the normalised kinetic energy dissipation rate in both single-phase and two-phase cases. In the case of single-phase flow (figure 2
a,c), one can clearly observe the large-scale plumes on the IC and OC for both
![]() $Re_{i}$
and that the plumes are noticeably more turbulent in the high-
$Re_{i}$
and that the plumes are noticeably more turbulent in the high-
![]() $Re_{i}$
case. The magnitude of dissipation is high around the plumes, owing to large strain rates, and also in the boundary layers on the IC and OC. Upon injection of bubbles (figure 2
b,d), the plumes originating from the IC no longer protrude into the bulk, but rather become a collection of small-scale intermittent plumes along the surface. Consequently, the turbulence levels in the bulk and near the OC are much weaker as compared to single-phase flow. The dispersed bubbles block/weaken the momentum transport such that turbulence is enhanced and confined to regions close to the IC, while it is strongly attenuated in the bulk and near the OC. Remarkably, the weakening of large-scale plumes by the bubbles and subsequent turbulence attenuation in the bulk and OC overpowers the turbulence enhancement near the IC, the combined effect of which leads to a net positive drag reduction.
$Re_{i}$
case. The magnitude of dissipation is high around the plumes, owing to large strain rates, and also in the boundary layers on the IC and OC. Upon injection of bubbles (figure 2
b,d), the plumes originating from the IC no longer protrude into the bulk, but rather become a collection of small-scale intermittent plumes along the surface. Consequently, the turbulence levels in the bulk and near the OC are much weaker as compared to single-phase flow. The dispersed bubbles block/weaken the momentum transport such that turbulence is enhanced and confined to regions close to the IC, while it is strongly attenuated in the bulk and near the OC. Remarkably, the weakening of large-scale plumes by the bubbles and subsequent turbulence attenuation in the bulk and OC overpowers the turbulence enhancement near the IC, the combined effect of which leads to a net positive drag reduction.

Figure 3. Radial profiles of angular velocity transport for
![]() $Re_{i}=5\times 10^{3}$
(blue solid lines) and
$Re_{i}=5\times 10^{3}$
(blue solid lines) and
![]() $Re_{i}=2\times 10^{4}$
(red dashed lines). Squares, circles and diamond markers correspond to
$Re_{i}=2\times 10^{4}$
(red dashed lines). Squares, circles and diamond markers correspond to
![]() $We=0.5,1,2$
, respectively. Horizontal lines represent the angular velocity flux for the corresponding single-phase flow.
$We=0.5,1,2$
, respectively. Horizontal lines represent the angular velocity flux for the corresponding single-phase flow.
To quantify the effect seen in figure 2, we look at the angular velocity transport from IC to OC. In single-phase flow, the angular velocity flux is conserved in the radial (wall-normal) direction i.e.
![]() $\unicode[STIX]{x2202}_{r}[r^{3}\langle u_{r}\unicode[STIX]{x1D714}\rangle -r^{3}\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{r}\langle \unicode[STIX]{x1D714}\rangle ]=\unicode[STIX]{x2202}_{r}[J_{\unicode[STIX]{x1D714}}]=0$
(Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). In two-phase flows, due to the forcing from the dispersed phase, this expression is corrected accordingly and is written as
$\unicode[STIX]{x2202}_{r}[r^{3}\langle u_{r}\unicode[STIX]{x1D714}\rangle -r^{3}\unicode[STIX]{x1D708}\unicode[STIX]{x2202}_{r}\langle \unicode[STIX]{x1D714}\rangle ]=\unicode[STIX]{x2202}_{r}[J_{\unicode[STIX]{x1D714}}]=0$
(Eckhardt, Grossmann & Lohse Reference Eckhardt, Grossmann and Lohse2007). In two-phase flows, due to the forcing from the dispersed phase, this expression is corrected accordingly and is written as
In these expressions,
![]() $J_{\unicode[STIX]{x1D714}}$
is the angular velocity flux,
$J_{\unicode[STIX]{x1D714}}$
is the angular velocity flux,
![]() $\unicode[STIX]{x1D714}$
is the angular velocity,
$\unicode[STIX]{x1D714}$
is the angular velocity,
![]() $u_{r}$
is the radial velocity,
$u_{r}$
is the radial velocity,
![]() $r$
is the wall-normal position,
$r$
is the wall-normal position,
![]() $\langle \,\cdots \,\rangle$
refers to averaging in the homogeneous directions (azimuthal and axial) and over time;
$\langle \,\cdots \,\rangle$
refers to averaging in the homogeneous directions (azimuthal and axial) and over time;
![]() $f_{\unicode[STIX]{x1D703}}$
is the forcing from the dispersed phase onto the carrier fluid in the azimuthal (streamwise) direction. The balance arises naturally from (2.1), following the same approach as described in Eckhardt et al. (Reference Eckhardt, Grossmann and Lohse2007), but with the inclusion of a source term in the momentum equation due to the dispersed bubbles. Here, we note that (3.2) is used as the convergence criteria for two-phase simulations. After this condition is satisfied, we collect statistics over approximately 20 full cylinder rotations. To analyse the stresses that are transported from the IC to OC, we plot the azimuthally, axially and time-averaged value of
$f_{\unicode[STIX]{x1D703}}$
is the forcing from the dispersed phase onto the carrier fluid in the azimuthal (streamwise) direction. The balance arises naturally from (2.1), following the same approach as described in Eckhardt et al. (Reference Eckhardt, Grossmann and Lohse2007), but with the inclusion of a source term in the momentum equation due to the dispersed bubbles. Here, we note that (3.2) is used as the convergence criteria for two-phase simulations. After this condition is satisfied, we collect statistics over approximately 20 full cylinder rotations. To analyse the stresses that are transported from the IC to OC, we plot the azimuthally, axially and time-averaged value of
![]() $J_{\unicode[STIX]{x1D714}}$
normalised with its corresponding laminar value
$J_{\unicode[STIX]{x1D714}}$
normalised with its corresponding laminar value
![]() $J_{lam}$
versus the normalised radial position in figure 3.
$J_{lam}$
versus the normalised radial position in figure 3.
As mentioned earlier, in single-phase flow,
![]() $J_{\unicode[STIX]{x1D714}}$
is constant along the radial position (cf. figure 3). In the presence of bubbles, the value
$J_{\unicode[STIX]{x1D714}}$
is constant along the radial position (cf. figure 3). In the presence of bubbles, the value
![]() $J_{\unicode[STIX]{x1D714}}$
is higher than that of single-phase flow close to the IC and relatively lower in the bulk and near the OC. A lower value of
$J_{\unicode[STIX]{x1D714}}$
is higher than that of single-phase flow close to the IC and relatively lower in the bulk and near the OC. A lower value of
![]() $J_{\unicode[STIX]{x1D714}}$
in comparison to the single-phase case indicates attenuation of turbulence in the flow, i.e. the bubbles reduce the radial and axial velocity fluctuations and in turn the stresses that are transported between the cylinders (in the case of purely laminar flow
$J_{\unicode[STIX]{x1D714}}$
in comparison to the single-phase case indicates attenuation of turbulence in the flow, i.e. the bubbles reduce the radial and axial velocity fluctuations and in turn the stresses that are transported between the cylinders (in the case of purely laminar flow
![]() $J_{\unicode[STIX]{x1D714}}/J_{lam}=1$
). Close to the IC,
$J_{\unicode[STIX]{x1D714}}/J_{lam}=1$
). Close to the IC,
![]() $J_{\unicode[STIX]{x1D714}}$
is much higher than that of a single-phase flow due to two effects. Firstly, collision of bubbles with the IC increases local dissipation in the region between the IC and the bulk. Second, as noted in figure 1(b), bubbles tend to prefer regions close to the inner cylinder due to centrifugal forces and, since we model the interfaces of bubbles with no-slip boundary conditions (contaminated interface), the fluid in between the inner cylinder and the surface of the bubbles is sheared strongly, which leads to an increase in dissipation. The increase in dissipation due to bubble accumulation near the walls is also seen in channel flows injected with bubbles (Dabiri, Lu & Tryggvason Reference Dabiri, Lu and Tryggvason2013). Furthermore, the wakes of the bubbles are also regions of intense dissipation, which can be observed in figure 2.
$J_{\unicode[STIX]{x1D714}}$
is much higher than that of a single-phase flow due to two effects. Firstly, collision of bubbles with the IC increases local dissipation in the region between the IC and the bulk. Second, as noted in figure 1(b), bubbles tend to prefer regions close to the inner cylinder due to centrifugal forces and, since we model the interfaces of bubbles with no-slip boundary conditions (contaminated interface), the fluid in between the inner cylinder and the surface of the bubbles is sheared strongly, which leads to an increase in dissipation. The increase in dissipation due to bubble accumulation near the walls is also seen in channel flows injected with bubbles (Dabiri, Lu & Tryggvason Reference Dabiri, Lu and Tryggvason2013). Furthermore, the wakes of the bubbles are also regions of intense dissipation, which can be observed in figure 2.
We now move on to understanding the role of deformability, i.e. the Weber number, on drag reduction. As shown in (3.1), the overall drag reduction
![]() $DR$
can be written as sum of two terms which correspond to two different physical effects. This formulation of
$DR$
can be written as sum of two terms which correspond to two different physical effects. This formulation of
![]() $DR$
is useful in distinguishing the various mechanisms by which a dispersed phase influences the carrier phase and consequently the overall drag in the flow. The first term on the right-hand side of (3.1) is a contribution from the cumulative effect of the reduction in dissipative vortex structures in the flow. If the overall dissipation in the two-phase case
$DR$
is useful in distinguishing the various mechanisms by which a dispersed phase influences the carrier phase and consequently the overall drag in the flow. The first term on the right-hand side of (3.1) is a contribution from the cumulative effect of the reduction in dissipative vortex structures in the flow. If the overall dissipation in the two-phase case
![]() $\langle \unicode[STIX]{x1D716}_{t}\rangle$
is less than that of the single-phase case
$\langle \unicode[STIX]{x1D716}_{t}\rangle$
is less than that of the single-phase case
![]() $\langle \unicode[STIX]{x1D716}_{s}\rangle$
,
$\langle \unicode[STIX]{x1D716}_{s}\rangle$
,
![]() $\langle DR_{1}\rangle =1-\langle \unicode[STIX]{x1D716}_{t}\rangle /\langle \unicode[STIX]{x1D716}_{s}\rangle$
contributes positively to the overall drag reduction. The second term
$\langle DR_{1}\rangle =1-\langle \unicode[STIX]{x1D716}_{t}\rangle /\langle \unicode[STIX]{x1D716}_{s}\rangle$
contributes positively to the overall drag reduction. The second term
![]() $\langle DR_{2}\rangle$
on the other hand is a contribution from the momentum transfer from the bubbles to the carrier liquid, and in a physical sense either assists or impedes the IC in driving the fluid depending on the sign of the term
$\langle DR_{2}\rangle$
on the other hand is a contribution from the momentum transfer from the bubbles to the carrier liquid, and in a physical sense either assists or impedes the IC in driving the fluid depending on the sign of the term
![]() $\langle DR\rangle _{2}$
. In figure 4(a), we plot the individual contributions from both these terms for the low- and high-
$\langle DR\rangle _{2}$
. In figure 4(a), we plot the individual contributions from both these terms for the low- and high-
![]() $Re_{i}$
cases. We find that the contribution from
$Re_{i}$
cases. We find that the contribution from
![]() $\langle DR_{1}\rangle$
increases significantly with deformation in comparison to
$\langle DR_{1}\rangle$
increases significantly with deformation in comparison to
![]() $\langle DR_{2}\rangle$
. The energy injection rate
$\langle DR_{2}\rangle$
. The energy injection rate
![]() $\langle DR\rangle _{2}$
does not change significantly in comparison with
$\langle DR\rangle _{2}$
does not change significantly in comparison with
![]() $\langle DR\rangle _{1}$
. This is expected, as due to the averaging in
$\langle DR\rangle _{1}$
. This is expected, as due to the averaging in
![]() $\langle DR\rangle _{2}$
in both space and time, the primary source of momentum transfer between the bubbles and the carrier fluid comes from the buoyancy of the bubbles, which does not change with deformability. In all cases, we ensure that every individual bubble has the same volume and is incompressible. It is also important to note here that in contrast to sub-Kolmogorov bubbles, because of the strong buoyancy of an individual finite-size bubble, they rarely get trapped in the descending part of the Taylor roll, which may lead to a negative
$\langle DR\rangle _{2}$
in both space and time, the primary source of momentum transfer between the bubbles and the carrier fluid comes from the buoyancy of the bubbles, which does not change with deformability. In all cases, we ensure that every individual bubble has the same volume and is incompressible. It is also important to note here that in contrast to sub-Kolmogorov bubbles, because of the strong buoyancy of an individual finite-size bubble, they rarely get trapped in the descending part of the Taylor roll, which may lead to a negative
![]() $\langle DR\rangle _{2}$
.
$\langle DR\rangle _{2}$
.

Figure 4. (a) Individual contributions from
![]() $\langle DR\rangle _{1}$
(squares) and
$\langle DR\rangle _{1}$
(squares) and
![]() $\langle DR\rangle _{2}$
(circles) to
$\langle DR\rangle _{2}$
(circles) to
![]() $DR$
versus Weber number for
$DR$
versus Weber number for
![]() $Re_{i}=5\times 10^{3}$
(blue solid lines) and
$Re_{i}=5\times 10^{3}$
(blue solid lines) and
![]() $Re_{i}=2\times 10^{4}$
(red dashed lines). (b) Probability distribution function of the bubble Reynolds number
$Re_{i}=2\times 10^{4}$
(red dashed lines). (b) Probability distribution function of the bubble Reynolds number
![]() $Re_{p}$
for different Weber numbers for
$Re_{p}$
for different Weber numbers for
![]() $Re_{i}=2\times 10^{4}$
. Arrow indicates increasing Weber number; colour coding of lines similar to figure 1.
$Re_{i}=2\times 10^{4}$
. Arrow indicates increasing Weber number; colour coding of lines similar to figure 1.
While the term
![]() $\langle DR\rangle _{1}$
is overall positive for all cases, it is negative only at low
$\langle DR\rangle _{1}$
is overall positive for all cases, it is negative only at low
![]() $Re_{i}$
with rigid bubbles. In this case, the dissipation in the wake generated by the rigid bubbles overcomes the dissipation in large-scale coherent structures. It is difficult to generalise this effect given that
$Re_{i}$
with rigid bubbles. In this case, the dissipation in the wake generated by the rigid bubbles overcomes the dissipation in large-scale coherent structures. It is difficult to generalise this effect given that
![]() $d_{b}/\unicode[STIX]{x1D702}_{K}$
is different for the low- and high-
$d_{b}/\unicode[STIX]{x1D702}_{K}$
is different for the low- and high-
![]() $Re_{i}$
cases. To understand the primary source of increasing drag reduction with increasing deformability, we must understand the trend of
$Re_{i}$
cases. To understand the primary source of increasing drag reduction with increasing deformability, we must understand the trend of
![]() $\langle DR\rangle _{1}$
, and for this we look into the effect of finite-size bubbles on the surrounding turbulent flow. Finite-size bubbles with sufficiently high slip velocity and particle (local) Reynolds number shed wakes which are additional sources of dissipation in the flow. While bubble wakes typically increase dissipation, the bubbles themselves also weaken the large-scale plumes which are the primary sources for momentum transport (cf. figures 2 and 3); the weakening of plumes overcomes the dissipation induced by bubbles’ wakes, thus leading to a net positive drag reduction. When the immersed bubbles are made more deformable by lowering their surface tension (or increasing the Weber number), they are stretched along the streamwise direction similar to that of sub-Kolmogorov deformable bubbles (Spandan et al.
Reference Spandan, Verzicco and Lohse2017b
). The stretching leads to a lower projected surface area in the direction of the relative velocity, which in turn leads to a lower bubble Reynolds number. This is shown in figure 4(b), where we plot the probability distribution function of the bubble Reynolds number defined as
$\langle DR\rangle _{1}$
, and for this we look into the effect of finite-size bubbles on the surrounding turbulent flow. Finite-size bubbles with sufficiently high slip velocity and particle (local) Reynolds number shed wakes which are additional sources of dissipation in the flow. While bubble wakes typically increase dissipation, the bubbles themselves also weaken the large-scale plumes which are the primary sources for momentum transport (cf. figures 2 and 3); the weakening of plumes overcomes the dissipation induced by bubbles’ wakes, thus leading to a net positive drag reduction. When the immersed bubbles are made more deformable by lowering their surface tension (or increasing the Weber number), they are stretched along the streamwise direction similar to that of sub-Kolmogorov deformable bubbles (Spandan et al.
Reference Spandan, Verzicco and Lohse2017b
). The stretching leads to a lower projected surface area in the direction of the relative velocity, which in turn leads to a lower bubble Reynolds number. This is shown in figure 4(b), where we plot the probability distribution function of the bubble Reynolds number defined as
![]() $Re_{p}=(|\boldsymbol{u}-\boldsymbol{v}|)\sqrt{4\bar{A}/\unicode[STIX]{x03C0}}/\unicode[STIX]{x1D708}$
for
$Re_{p}=(|\boldsymbol{u}-\boldsymbol{v}|)\sqrt{4\bar{A}/\unicode[STIX]{x03C0}}/\unicode[STIX]{x1D708}$
for
![]() $Re_{i}=2\times 10^{4}$
. Here it is important to note that the exact calculation of particle Reynolds number in simulations involving IBM is non-trivial as the local fluid velocity
$Re_{i}=2\times 10^{4}$
. Here it is important to note that the exact calculation of particle Reynolds number in simulations involving IBM is non-trivial as the local fluid velocity
![]() $\boldsymbol{u}$
in
$\boldsymbol{u}$
in
![]() $Re_{p}$
is ill-defined. A discussion on the calculation is given in the Appendix.
$Re_{p}$
is ill-defined. A discussion on the calculation is given in the Appendix.
It is easily seen that the bubble Reynolds number distribution is much wider for rigid non-deformable (
![]() $We=0.01$
) bubbles in comparison to deformable (
$We=0.01$
) bubbles in comparison to deformable (
![]() $We=2.0$
) bubbles. We have found no significant differences in the distribution of the relative velocities between individual bubbles and the local fluid velocity
$We=2.0$
) bubbles. We have found no significant differences in the distribution of the relative velocities between individual bubbles and the local fluid velocity
![]() $|\boldsymbol{u}-\boldsymbol{v}|$
; the differences in the projected areas of the bubbles (
$|\boldsymbol{u}-\boldsymbol{v}|$
; the differences in the projected areas of the bubbles (
![]() $\bar{A}$
) is the primary source of differences in the distribution of
$\bar{A}$
) is the primary source of differences in the distribution of
![]() $Re_{p}$
. The Reynolds numbers of deformable bubbles are much lower in comparison to those of rigid non-deformable bubbles, which corresponds to a relatively lower dissipation induced in the flow by the bubble wake. Thus, while the energy injection rate from the bubbles remains roughly the same for bubbles with varying Weber numbers, the dissipation originating from the bubbles’ wakes decreases with increasing deformability. This leads to a positive contribution to the drag reduction from the term
$Re_{p}$
. The Reynolds numbers of deformable bubbles are much lower in comparison to those of rigid non-deformable bubbles, which corresponds to a relatively lower dissipation induced in the flow by the bubble wake. Thus, while the energy injection rate from the bubbles remains roughly the same for bubbles with varying Weber numbers, the dissipation originating from the bubbles’ wakes decreases with increasing deformability. This leads to a positive contribution to the drag reduction from the term
![]() $\langle DR\rangle _{1}$
. When the bubbles are non-deformable, the positive contribution to
$\langle DR\rangle _{1}$
. When the bubbles are non-deformable, the positive contribution to
![]() $DR$
induced by the momentum forcing term
$DR$
induced by the momentum forcing term
![]() $\langle DR\rangle _{2}$
is compensated by the dissipation arising from the wake of non-deformable bubbles, as can be seen for
$\langle DR\rangle _{2}$
is compensated by the dissipation arising from the wake of non-deformable bubbles, as can be seen for
![]() $We=0.01$
in figure 4(a). This is shown qualitatively by visualising isocontours of vortical structures through the Q-criterion in figure 5. While one can clearly see the coherent Taylor rolls for the single-phase case, with the inclusion of bubbles, dissipative vortices change completely, with a high concentration near the inner cylinder. In the case of high Weber number, the dissipative structures are much weaker as compared to that of the flow with rigid bubbles.
$We=0.01$
in figure 4(a). This is shown qualitatively by visualising isocontours of vortical structures through the Q-criterion in figure 5. While one can clearly see the coherent Taylor rolls for the single-phase case, with the inclusion of bubbles, dissipative vortices change completely, with a high concentration near the inner cylinder. In the case of high Weber number, the dissipative structures are much weaker as compared to that of the flow with rigid bubbles.

Figure 5. Vortical structures mapped using the Q-criterion for
![]() $Re_{i}=5\times 10^{3}$
(a) Single phase. (b) Two-phase
$Re_{i}=5\times 10^{3}$
(a) Single phase. (b) Two-phase
![]() $We\sim 0$
. (c) Two-phase
$We\sim 0$
. (c) Two-phase
![]() $We\sim 2.0$
.
$We\sim 2.0$
.
4 Summary and outlook
With the help of fully resolved numerical simulations, we have been able to identify different physical effects and their individual contributions to bubble-induced drag reduction in turbulent Taylor–Couette (TC) flow. We show that drag reduction in two-phase TC flow is an effect of the bubbles weakening the large-scale plumes responsible for momentum transport. The net effect of immersed bubbles is that in comparison to single-phase flow, turbulence near the inner cylinder is enhanced (due to dissipation between the bubbles and the bounding wall, and from bubble wake and bubble collision with walls) while turbulence is attenuated in the bulk and near the outer cylinder (due to bubbles blocking the momentum transfer between the cylinders). Furthermore, we have identified different physical mechanisms and their corresponding contributions to drag reduction. The net drag reduction is written as a sum of two terms which are contributions from (i) changes in dissipative structures in the flow and (ii) an energy injection rate from the dispersed bubbles. We find that the intensity of dissipative structures in the flow decreases with increasing deformability. Due to stretching in the streamwise direction, deformable bubbles have on average a lower local Reynolds number in comparison to non-deformable bubbles, which leads to reduced dissipation in the flow. While the energy injection rate from the bubbles always contributes to drag reduction, the net effect from dissipation becomes the governing factor in achieving significant drag reduction.
The current numerical simulations only operate in the regime where coalescence and breakup of bubbles is avoided, which ensures a mono-dispersed bubble distribution. However, in a real system, coalescence and breakup of bubbles might lead to a distribution of sizes, in which case their effect on the underlying turbulent structures may vary, and we are currently working on implementing these features within our numerical framework.
Acknowledgements
This work was supported by the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation programme funded by the Ministry of Education, Culture and Science of the government of the Netherlands. The simulations were carried out on the national e-infrastructure of SURFsara, a subsidiary of the SURF cooperation, the collaborative ICT organisation for Dutch education and research. We also acknowledge PRACE for awarding us access to the Marconi super computer, based in Italy at CINECA under PRACE project number 2016143351.
Appendix
In numerical simulations involving fully resolved techniques (such as IBM), calculating
![]() $Re_{p}$
is extremely non-trivial for two primary reasons. First, while the mean bubble velocity (
$Re_{p}$
is extremely non-trivial for two primary reasons. First, while the mean bubble velocity (
![]() $\boldsymbol{v}$
) is clearly defined and is computed in the simulation, the mean fluid velocity (
$\boldsymbol{v}$
) is clearly defined and is computed in the simulation, the mean fluid velocity (
![]() $\boldsymbol{u}$
) that the bubble experiences needs to be computed through a filtering approach. In this paper, we compute the mean of the fluid velocity interpolated at the end of a probe from each Lagrangian marker (see Spandan et al. (Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a
) for more details on the probe technique). Second, the calculation of a mean projected area of a deformable body along specific directions is done using a coarse-grained ray-tracing technique. This is achieved by computing the projected areas of individual Eulerian cells immersed inside the bubble along specific directions; the mean projected area is then computed as
$\boldsymbol{u}$
) that the bubble experiences needs to be computed through a filtering approach. In this paper, we compute the mean of the fluid velocity interpolated at the end of a probe from each Lagrangian marker (see Spandan et al. (Reference Spandan, Meschini, Ostilla-Mónico, Lohse, Querzoli, de Tullio and Verzicco2017a
) for more details on the probe technique). Second, the calculation of a mean projected area of a deformable body along specific directions is done using a coarse-grained ray-tracing technique. This is achieved by computing the projected areas of individual Eulerian cells immersed inside the bubble along specific directions; the mean projected area is then computed as
![]() $\bar{A}=\sum _{i=1}^{i=3}\unicode[STIX]{x1D6FE}_{i}A_{i}$
, where
$\bar{A}=\sum _{i=1}^{i=3}\unicode[STIX]{x1D6FE}_{i}A_{i}$
, where
![]() $\unicode[STIX]{x1D6FE}_{i}$
are the direction cosines of the relative velocity vector and
$\unicode[STIX]{x1D6FE}_{i}$
are the direction cosines of the relative velocity vector and
![]() $A_{i}$
is the projected area in the
$A_{i}$
is the projected area in the
![]() $i$
th direction.
$i$
th direction.