Article contents
The planar X-junction flow: stability analysis and control
Published online by Cambridge University Press: 16 July 2014
Abstract
The bifurcations and control of the flow in a planar X-junction are studied via linear stability analysis and direct numerical simulations. This study reveals the instability mechanisms in a symmetric channel junction and shows how these can be stabilized or destabilized by boundary modification. We observe two bifurcations as the Reynolds number increases. They both scale with the inlet speed of the two side channels and are almost independent of the inlet speed of the main channel. Equivalently, both bifurcations appear when the recirculation zones reach a critical length. A two-dimensional stationary global mode becomes unstable first, changing the flow from a steady symmetric state to a steady asymmetric state via a pitchfork bifurcation. The core of this instability, whether defined by the structural sensitivity or by the disturbance energy production, is at the edges of the recirculation bubbles, which are located symmetrically along the walls of the downstream channel. The energy analysis shows that the first bifurcation is due to a lift-up mechanism. We develop an adjustable control strategy for the first bifurcation with distributed suction or blowing at the walls. The linearly optimal wall-normal velocity distribution is computed through a sensitivity analysis and is shown to delay the first bifurcation from 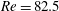 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=82.5$ to
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=82.5$ to 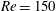 $\mathit{Re}=150$ . This stabilizing effect arises because blowing at the walls weakens the wall-normal gradient of the streamwise velocity around the recirculation zone and hinders the lift-up. At the second bifurcation, a three-dimensional stationary global mode with a spanwise wavenumber of order unity becomes unstable around the asymmetric steady state. Nonlinear three-dimensional simulations at the second bifurcation display transition to a nonlinear cycle involving growth of a three-dimensional steady structure, time-periodic secondary instability and nonlinear breakdown restoring a two-dimensional flow. Finally, we show that the sensitivity to wall suction at the second bifurcation is as large as it is at the first bifurcation, providing a possible mechanism for destabilization.
$\mathit{Re}=150$ . This stabilizing effect arises because blowing at the walls weakens the wall-normal gradient of the streamwise velocity around the recirculation zone and hinders the lift-up. At the second bifurcation, a three-dimensional stationary global mode with a spanwise wavenumber of order unity becomes unstable around the asymmetric steady state. Nonlinear three-dimensional simulations at the second bifurcation display transition to a nonlinear cycle involving growth of a three-dimensional steady structure, time-periodic secondary instability and nonlinear breakdown restoring a two-dimensional flow. Finally, we show that the sensitivity to wall suction at the second bifurcation is as large as it is at the first bifurcation, providing a possible mechanism for destabilization.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
Footnotes
The original version of this article was published with incorrect affiliations for O. Tammisola, V. Citro and M. P. Juniper. A notice detailing this has been published online and in print, and the error rectified in the print and the online PDF and HTML copies.
References
A correction has been issued for this article:
- 38
- Cited by
Linked content
Please note a has been issued for this article.

