Article contents
A population balance model for large eddy simulation of polydisperse droplet evolution
Published online by Cambridge University Press: 18 September 2019
Abstract
In the context of many applications of turbulent multi-phase flows, knowledge of the dispersed phase size distribution and its evolution is critical to predicting important macroscopic features. We develop a large eddy simulation (LES) model that can predict the turbulent transport and evolution of size distributions, for a specific subset of applications in which the dispersed phase can be assumed to consist of spherical droplets, and occurring at low volume fraction. We use a population dynamics model for polydisperse droplet distributions specifically adapted to a LES framework including a model for droplet breakup due to turbulence, neglecting coalescence consistent with the assumed small dispersed phase volume fractions. We model the number density fields using an Eulerian approach for each bin of the discretized droplet size distribution. Following earlier methods used in the Reynolds-averaged Navier–Stokes framework, the droplet breakup due to turbulent fluctuations is modelled by treating droplet–eddy collisions as in kinetic theory of gases. Existing models assume the scale of droplet–eddy collision to be in the inertial range of turbulence. In order to also model smaller droplets comparable to or smaller than the Kolmogorov scale we extend the breakup kernels using a structure function model that smoothly transitions from the inertial to the viscous range. The model includes a dimensionless coefficient that is fitted by comparing predictions in a one-dimensional version of the model with a laboratory experiment of oil droplet breakup below breaking waves. After initial comparisons of the one-dimensional model to measurements of oil droplets in an axisymmetric jet, it is then applied in a three-dimensional LES of a jet in cross-flow with large oil droplets of a single size being released at the source of the jet. We model the concentration fields using 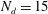 $N_{d}=15$ bins of discrete droplet sizes and solve scalar transport equations for each bin. The resulting droplet size distributions are compared with published experimental data, and good agreement for the relative size distribution is obtained. The LES results also enable us to quantify size distribution variability. We find that the probability distribution functions of key quantities such as the total surface area and the Sauter mean diameter of oil droplets are highly variable, some displaying strong non-Gaussian intermittent behaviour.
$N_{d}=15$ bins of discrete droplet sizes and solve scalar transport equations for each bin. The resulting droplet size distributions are compared with published experimental data, and good agreement for the relative size distribution is obtained. The LES results also enable us to quantify size distribution variability. We find that the probability distribution functions of key quantities such as the total surface area and the Sauter mean diameter of oil droplets are highly variable, some displaying strong non-Gaussian intermittent behaviour.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 51
- Cited by

