Published online by Cambridge University Press: 24 October 2011
Results from direct numerical simulation for three-dimensional Rayleigh–Bénard convection in samples of aspect ratio 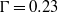 and
and 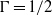 up to Rayleigh number
up to Rayleigh number 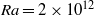 are presented. The broad range of Prandtl numbers
are presented. The broad range of Prandtl numbers 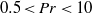 is considered. In contrast to some experiments, we do not see any increase in
is considered. In contrast to some experiments, we do not see any increase in 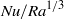 with increasing
with increasing 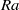 , neither due to an increasing
, neither due to an increasing 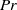 , nor due to constant heat flux boundary conditions at the bottom plate instead of constant temperature boundary conditions. Even at these very high
, nor due to constant heat flux boundary conditions at the bottom plate instead of constant temperature boundary conditions. Even at these very high 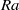 , both the thermal and kinetic boundary layer thicknesses obey Prandtl–Blasius scaling.
, both the thermal and kinetic boundary layer thicknesses obey Prandtl–Blasius scaling.
Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.
Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.
Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.
Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.
Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 1.
Movie of the temperature field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 1.
Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 2.
Movie of the vertical velocity field in a vertical cut for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie. This vertical cut is perpendicular to the plane shown in movie 2.
Movie of the temperature in three horizontal planes (0:25z/L, 0:50z/L, and 0:75z/L) for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.
Movie of the temperature in three horizontal planes (0:25z/L, 0:50z/L, and 0:75z/L) for the simulation at Ra = 2 x 1012 and Pr = 0.7 in an aspect ratio Γ = 0.5 sample. The dimensionless time is indicated in the top of the movie.