Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T10:29:07.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Progression of heavy plates from stable falling to tumbling flight

Published online by Cambridge University Press:  11 July 2018

Edwin M. Lau ,
Wei-Xi Huang Open the ORCID record for Wei-Xi Huang [Opens in a new window]  and
Chun-Xiao Xu Open the ORCID record for Chun-Xiao Xu [Opens in a new window]
Edwin M. Lau
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Wei-Xi Huang*
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Chun-Xiao Xu
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: hwx@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

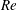This study examines the transition of stable falling to tumbling flight for freely falling heavy plates in a two-dimensional viscous fluid, solved via direct numerical simulation with the immersed boundary method. The simulations are performed at a range of Reynolds number ($Re$) of up to 500 and a dimensionless moment of inertia (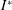$I^{\ast }$) up to 10. It is found that a plate may settle to stable falling or develop into tumbling descent depending on the initial angle of release 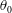$\unicode[STIX]{x1D703}_{0}$. The characteristics and performance that distinguish two flight states are investigated. This bistability is analysed with phase portraits and the region mapped across the regime of 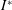$I^{\ast }$ and 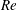$Re$ at a specific thickness ratio. In determining the flight state, the respective critical 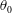$\unicode[STIX]{x1D703}_{0}$ is found to follow a power law through 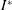$I^{\ast }$ and 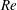$Re$. It is suggested that the changing slope of the lift curve that the plate undergoes sets the two flight states apart. Flow fields also reveal that the recirculation behind the plate is confined by the vortex structures and provides an additional rotation to the plate. An experiment is performed suggesting that bistability also occurs at Re 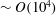${\sim}O(10^{4})$. Other shapes are also simulated and the different bistable effects are discussed.

JFM classification

Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 1009 - 1031
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, A., Pesavento, U. & Wang, Z. J. 2005a Analysis of transitions between fluttering, tumbling and steady descent of falling cards. J. Fluid Mech. 541, 91–104.Google Scholar
Andersen, A., Pesavento, U. & Wang, Z. J. 2005b Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.Google Scholar
Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of disks. J. Fluid Mech. 719, 388–405.Google Scholar
Belmonte, A., Shelley, M. J., Eldakar, S. T. & Wiggins, C. H. 2001 Dynamic patterns and self-knotting of a driven hanging chain. Phys. Rev. Lett. 87 (11), 345–348.Google Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25 (4), 044102.Google Scholar
Dupleich, P.1941 Rotation in free fall of rectangular wings of elongated shape. NASA Tech. Mem. 1201.Google Scholar
Dušek, J., Chrust, M. & Bouchet, G. 2016 Transitional dynamics of freely falling discs. In Advances in Fluid-Structure Interaction, vol. 133, pp. 105–116.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44 (1), 97–121.Google Scholar
Field, S. B., Klaus, M. & Moore, M. G. 1997 Chaotic dynamics of falling disks. Nature 388, 252–254.Google Scholar
Fonseca, F. & Herrmann, H. J. 2005 Simulation of the sedimentation of a falling oblate ellipsoid. Physica A 345 (3–4), 341–355.Google Scholar
Heisinger, L., Newton, P. & Kanso, E. 2014 Coins falling in water. J. Fluid Mech. 742, 243–253.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.Google Scholar
Hu, R. & Wang, L. 2014 Motion transitions of falling plates via quasisteady aerodynamics. Phys. Rev. E 90 (1), 013020.Google Scholar
Huang, W.-X., Shin, S. J. & Sung, H. J. 2007 Simulation of flexible filaments in a uniform flow by the immersed boundary method. J. Comput. Phys. 226 (2), 2206–2228.Google Scholar
Kim, J., Kim, D. & Choi, H. 2001 An immersed-boundary finite-volume method for simulations of flow in complex geometries. J. Comput. Phys. 171 (1), 132–150.Google Scholar
Kolomenskiy, D. & Schneider, K. 2009 Numerical simulations of falling leaves using a pseudo-spectral method with volume penalization. Theor. Comput. Fluid Dyn. 24 (1–4), 169–173.Google Scholar
Kuznetsov, S. P. 2015 Plate falling in a fluid: regular and chaotic dynamics of finite-dimensional models. Regular Chaotic Dyn. 20 (3), 345–382.Google Scholar
Lamb, H. 1945 Hydrodynamics. Dover.Google Scholar
Mathai, V., Zhu, X., Sun, C. & Lohse, D. 2017 Mass and moment of inertia govern the transition in the dynamics and wakes of freely rising and falling cylinders. Phys. Rev. Lett. 133, 054501.Google Scholar
Maxwell, J. C. 1852 Draft of paper on the descent of a body in a resisting medium. In The scientific letters and papers of James Clerk Maxwell (ed. Harman, P. M.), pp. 213–218. Cambridge University Press.Google Scholar
Mittal, R., Seshadri, V. & Udaykumar, H. S. 2004 Flutter, tumble and vortex induced autorotation. Theor. Comput. Fluid Dyn. 17 (3), 165–170.Google Scholar
Okamoto, M. & Azuma, A. 2011 Aerodynamic characteristics at low Reynolds numbers for wings of various planforms. AIAA J. 49 (6), 054501.Google Scholar
Paidoussis, M., Price, S. & Langre, E. 2011 Fluid-Structure Interactions Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Pesavento, U. & Wang, Z. J. 2004 Falling paper: Navier–Stokes solutions, model of fluid forces, and center of mass elevation. Phys. Rev. Lett. 93 (14), 144501.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numer. 11, 479–517.Google Scholar
Smith, E. H. 1971 Autorotating wings: an experimental investigation. J. Fluid Mech. 50, 513–534.Google Scholar
Sun, Q. & Boyd, I. D. 2004 Flat-plate aerodynamics at very low Reynolds number. J. Fluid Mech. 502, 199–206.Google Scholar
Wan, H., Dong, H. & Liang, Z. 2012 Vortex formation of freely falling plates. In 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA Paper 2012-1079.Google Scholar
Wang, W. B., Hu, R. F., Xu, S. J. & Wu, Z. N. 2013 Influence of aspect ratio on tumbling plates. J. Fluid Mech. 733, 650–679.Google Scholar
Wang, Y., Shu, C., Teo, C. J. & Yang, L. M. 2016 Numerical study on the freely falling plate: effects of density ratio and thickness-to-length ratio. Phys. Fluids 28 (10), 103603.Google Scholar
Willmarth, W. W., Hawk, N. E. & Harvey, R. L. 1964 Steady and unsteady motions and wakes of freely falling disks. Phys. Fluids 7 (2), 197–208.Google Scholar
Wu, R.-J. & Lin, S.-Y. 2015 The flow of a falling ellipse: numerical method and classification. J. Mech. 31 (06), 771–782.Google Scholar
Zhong, H., Lee, C., Su, Z., Chen, S., Zhou, M. & Wu, J. 2013 Experimental investigation of freely falling thin disks. Part 1. The flow structures and Reynolds number effects on the zigzag motion. J. Fluid Mech. 716, 228–250.Google Scholar
Zhou, W., Chrust, M. & Dušek, J. 2017 Path instabilities of oblate spheroids. J. Fluid Mech. 833, 445–468.Google Scholar