Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-28T03:18:12.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Progressive flexural–gravity waves with constant vorticity

Published online by Cambridge University Press:  23 October 2020

Z. Wang Open the ORCID record for Z. Wang [Opens in a new window] ,
X. Guan  and
J.-M. Vanden-Broeck
Z. Wang*
Affiliation:
Key Laboratory for Mechanics in Fluid–Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing100190, PR China State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing100190, PR China School of Engineering Science, University of Chinese Academy of Sciences, Beijing100049, PR China
X. Guan
Affiliation:
Key Laboratory for Mechanics in Fluid–Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing100190, PR China School of Engineering Science, University of Chinese Academy of Sciences, Beijing100049, PR China
J.-M. Vanden-Broeck
Affiliation:
Department of Mathematics, University College London, LondonWC1E 6BT, UK
*
†Email address for correspondence: zwang@imech.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

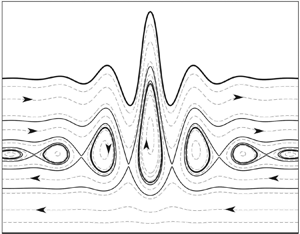
This paper is concerned with the interaction of vertically sheared currents with two-dimensional flexural–gravity waves in finite depth. A third-order Stokes expansion is carried out and fully nonlinear computations are performed for symmetric, steadily travelling waves on a linear shear current. For upstream periodic waves, two global bifurcation mechanisms are discovered. Both branches bifurcate from infinitesimal periodic waves, with one stopping at another infinitesimal wave of different phase speed, and the other terminating at a stationary configuration. Generalised solitary waves are found for downstream waves. More surprisingly, the central pulse of the generalised solitary wave can become wide and flat as the computational domain is enlarged. This provides strong evidence for the existence of wave fronts in single-layer free-surface waves. Particle trajectories and streamline structures are studied numerically for the fully nonlinear equations. Two patterns, closed orbits and pure horizontal transport, are observed for both periodic and solitary waves in moving frames. The most striking phenomenon is the existence of net vertical transport of particles beneath some solitary waves due to wave–current interactions. The streamline patterns alternate between net vertical transport and a closed orbit, resulting in the formation of a series of nested cat's-eye structures.

JFM classification

Waves/Free-surface Flows: Shear waves Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Solitary waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 905 , 25 December 2020 , A12
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akers, B. F., Ambrose, D. M., Pond, K. & Wright, J. D. 2016 Overturned internal capillary–gravity waves. Eur. J. Mech.-B/Fluids 57, 143–151.CrossRefGoogle Scholar
Akers, B. F., Ambrose, D. M. & Sulon, D. W. 2017 Periodic traveling interfacial hydroelastic waves with or without mass. Z. Angew. Math. Phys. 68, 141.CrossRefGoogle Scholar
Beale, T. J. 1991 Exact solitary water waves with capillary ripples at infinity. Commun. Pure Appl. Maths 44 (2), 211–257.CrossRefGoogle Scholar
Bhattacharjee, J. & Sahoo, T. 2009 Interaction of flexural gravity waves with shear current in shallow water. Ocean Engng 36, 831–841.CrossRefGoogle Scholar
Borluk, H. & Kalisch, H. 2012 Particle dynamics in the KdV approximation. Wave Motion 49, 691–709.CrossRefGoogle Scholar
Champneys, A. R., Vanden-Broeck, J.-M. & Lord, G. J. 2002 Do true elevation gravity-capillary solitary waves exist? A numerical investigation. J. Fluid Mech. 454, 403–417.CrossRefGoogle Scholar
Choi, W. 2009 Nonlinear surface waves interacting with a linear shear current. Maths Comput. Simul. 80 (1), 29–36.CrossRefGoogle Scholar
Constantin, A. 2006 The trajectories of particles in Stokes waves. Invent. Math. 166, 523–35.CrossRefGoogle Scholar
Constantin, A. & Strauss, W. 2004 Exact steady periodic water waves with vorticity. Commun. Pure Appl. Maths 57 (4), 481–527.CrossRefGoogle Scholar
Constantin, A. & Strauss, W. 2010 Pressure beneath a Stokes wave. Commun. Pure Appl. Maths 63, 533–557.Google Scholar
Curtis, C. W., Carter, J. D. & Kalisch, H. 2018 Particle paths in nonlinear Schrödinger models in the presence of linear shear currents. J. Fluid Mech. 855, 322–350.CrossRefGoogle Scholar
Dias, F. & Vanden-Broeck, J.-M. 2003 On internal fronts. J. Fluid Mech. 479, 145–154.CrossRefGoogle Scholar
Ehrnström, M. & Villari, G. 2008 Linear water waves with vorticity: rotational features and particle paths. J. Differ. Equ. 244, 1888–1909.CrossRefGoogle Scholar
Fochesato, C., Dias, F. & Grimshaw, R. 2005 Generalized solitary waves and fronts in coupled Korteweg-de Vries systems. Physica D 210, 96–117.CrossRefGoogle Scholar
Forbes, L. K. 1986 Surface waves of large amplitude beneath an elastic sheet. Part 1. High-order series solution. J. Fluid Mech. 169, 409–428.CrossRefGoogle Scholar
Gao, T. & Vanden-Broeck, J.-M. 2014 Numerical studies of two-dimensional hydroelastic periodic and generalised solitary waves. Phys. Fluids 26 (8), 087101.CrossRefGoogle Scholar
Gao, T., Wang, Z. & Milewski, P. A. 2019 Nonlinear hydroelastic waves on a linear shear current at finite depth. J. Fluid Mech. 876, 55–86.CrossRefGoogle Scholar
Gao, T., Wang, Z. & Vanden-Broeck, J.-M. 2016 New hydroelastic solitary waves in deep water and their dynamics. J. Fluid Mech. 788, 469–491.CrossRefGoogle Scholar
Greenhill, A. G. 1886 Wave motion in hydrodynamics. Am. J. Maths 9 (1), 62–96.CrossRefGoogle Scholar
Greenhill, A. G. 1916 Skating on thin ice. Phil. Mag. 31, 1–22.CrossRefGoogle Scholar
Grue, J. & Kolaas, J. 2017 Experimental particle paths and drift velocity in steep waves at finite water depth. J. Fluid Mech. 810, R1.CrossRefGoogle Scholar
Guyenne, P. & Părău, E. I. 2012 Computations of fully nonlinear hydroelastic solitary waves on deep water. J. Fluid Mech. 713, 307–329.CrossRefGoogle Scholar
Guyenne, P. & Părău, E. I. 2014 Finite-depth effects on solitary waves in a floating ice sheet. J. Fluid Struct. 49, 242–262.CrossRefGoogle Scholar
Hoefer, M. A., Smyth, N. F. & Sprenger, P. 2019 Modulation theory solution for nonlinearly resonant, fifth-order Korteweg-de Vries, nonclassical, traveling dispersive shock waves. Stud. Appl. Maths 142, 219–240.CrossRefGoogle Scholar
Hsu, H., Francius, M., Montalvo, P. & Kharif, C. 2016 Gravity-capillary waves in finite depth on flows of constant vorticity. Proc. R. Soc. A 472, 20160363.CrossRefGoogle ScholarPubMed
Hsu, H., Kharif, C., Abid, M. & Chen, Y. 2018 A nonlinear Schrödinger equation for gravity-capillary water waves on arbitrary depth with constant vorticity. Part 1. J. Fluid Mech. 854, 146–163.CrossRefGoogle Scholar
Hunter, J. K. & Vanden-Broeck, J.-M. 1983 Solitary and periodic gravity-capillary waves of finite amplitude. J. Fluid Mech. 134, 205–219.CrossRefGoogle Scholar
Kishida, N. & Sobey, R. J. 1988 Stokes theory for waves on linear shear current. J. Engng Mech. 114 (8), 1317–1334.Google Scholar
Longuet-Higgins, M. S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 245, 535–581.Google Scholar
Marko, J. R. 2003 Observations and analyses of an intense waves-in-ice event in the Sea of Okhotsk. J. Geophys. Res. 108, 3296.CrossRefGoogle Scholar
Matioc, B.-V. 2014 Global bifurcation for water waves with capillary effects and constant vorticity. Monatsh. Maths 174, 459–475.CrossRefGoogle Scholar
Milewski, P. A., Vanden-Broeck, J.-M. & Wang, Z. 2011 Hydroelastic solitary waves in deep water. J. Fluid Mech. 679, 628–640.CrossRefGoogle Scholar
Milewski, P. A. & Wang, Z. 2013 Three dimensional flexural–gravity waves. Stud. Appl. Maths 131, 135–148.CrossRefGoogle Scholar
Milinazzo, F. A. & Saffman, P. G. 1990 Effect of a surface shear layer on gravity and gravity-capillary waves of permanent form. J. Fluid Mech. 216, 93–101.CrossRefGoogle Scholar
Părău, E. I. & Dias, F. 2002 Nonlinear effects in the response of a floating ice plate to a moving load. J. Fluid Mech. 460, 281–305.CrossRefGoogle Scholar
Peake, N. 2001 Nonlinear stability of a fluid-loaded elastic plate with mean flow. J. Fluid Mech. 434, 101–118.CrossRefGoogle Scholar
Peake, N. 2004 On the unsteady motion of a long fluid-loaded elastic plate with mean flow. J. Fluid Mech. 507, 335–366.CrossRefGoogle Scholar
Plotnikov, P. I. & Toland, J. F. 2011 Modelling nonlinear hydroelastic waves. Phil. Trans. R. Soc. Lond. A 369, 2942–2956.Google ScholarPubMed
Ribeiro, R., Milewski, P. A. & Nachbin, A. 2017 Flow structure beneath rotational water waves with stagnation points. J. Fluid Mech. 812, 792–814.CrossRefGoogle Scholar
van der Sanden, J. J. & Short, N. H. 2017 Radar satellites measure ice cover displacements induced by moving vehicles. Cold Regions Sci. Technol. 133, 56–62.CrossRefGoogle Scholar
Segal, B. L., Moldabayev, D., Kalisch, H. & Deconinck, B. 2017 Explicit solutions for a long wave model with constant vorticity. Eur. J. Mech.-B/Fluids 65, 247–256.CrossRefGoogle Scholar
Simmen, J. A. & Saffman, P. G. 1985 Steady deep water waves on a linear shear current. Stud. Appl. Maths 73, 35–57.CrossRefGoogle Scholar
Sprenger, P. & Hoefer, M. A. 2017 Shock waves in dispersive hydrodynamics with nonconvex dispersion. SIAM J. Appl. Maths 77 (1), 26–50.CrossRefGoogle Scholar
Sprenger, P. & Hoefer, M. A. 2020 Discontinuous shock solutions of the Whitham modulation equations and traveling wave solutions of higher order dispersive nonlinear wave equations. Nonlinearity 33, 3268–3302.CrossRefGoogle Scholar
Squire, V., Hosking, R. J., Kerr, A. D. & Langhorne, P. J. 1996 Moving Loads on Ice Plates, Solid Mechanics and Its Applications. Kluwer.CrossRefGoogle Scholar
Squire, V., Robinson, W., Langhorne, P. & Haskell, T. 1988 Vehicles and aircraft on floating ice. Nature 333 (6169), 159–161.CrossRefGoogle Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–473.Google Scholar
Takizawa, T. 1988 Response of a floating sea ice sheet to a steadily moving load. J. Geophys. Res. 93, 5100–5112.CrossRefGoogle Scholar
Teles Da Silva, A. F. & Peregrine, D. H. 1988 Steep, steady surface waves on water of finite depth with constant vorticity. J. Fluid Mech. 195, 281–302.CrossRefGoogle Scholar
Thomas, R., Kharif, C. & Manna, M. 2012 A nonlinear Schrödinger equation for water waves on finite depth with constant vorticity. Phys. Fluids 24, 127102.CrossRefGoogle Scholar
Toland, J. F. 2007 Heavy hydroelastic travelling waves. Proc. R. Soc. A 463, 2371–2397.CrossRefGoogle Scholar
Trichtchenko, O., Milewski, P. A., Părău, E. I. & Vanden-Broeck, J.-M. 2019 Stability of periodic travelling flexural–gravity waves in two dimensions. Stud. Appl. Maths 142, 65–90.CrossRefGoogle Scholar
Trichtchenko, O., Părău, E. I., Vanden-Broeck, J.-M. & Milewski, P. A. 2018 Solitary flexural–gravity waves in three dimensions. Phil. Trans. R. Soc. Lond. 376 (2129), 20170345.Google ScholarPubMed
Turner, R. E. L. & Vanden-Broeck, J.-M. 1988 Broadening of interfacial solitary waves. Phys. Fluids 31, 2486–2490.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1994 Steep solitary waves in water of finite depth with constant vorticity. J. Fluid Mech. 274, 339–348.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. & Părău, E. I. 2011 Two-dimensional generalized solitary waves and periodic waves under an ice sheet. Phil. Trans. R. Soc. Lond. A 369, 2957–2972.Google ScholarPubMed
Wahlén, E. 2009 Steady water waves with a critical layer. J. Differ. Equ. 246, 2468–2483.CrossRefGoogle Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. John Wiley & Sons.Google Scholar
Wilton, J. R. 1915 On ripples. Phil. Mag. 29 (173), 688–700.CrossRefGoogle Scholar
Xia, X. & Shen, H. T. 2002 Nonlinear interaction of ice cover with shallow water waves in channels. J. Fluid Mech. 467, 259–268.CrossRefGoogle Scholar