Article contents
A ‘reciprocal’ theorem for the prediction of loads on a body moving in an inhomogeneous flow at arbitrary Reynolds number – CORRIGENDUM
Published online by Cambridge University Press: 05 December 2011
Extract
In Magnaudet (2011) an inertial contribution was overlooked during the derivation of (3.6). Indeed, when generalizing (E.5), which is valid for an irrotational velocity field 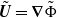 , to (E.6) which holds for any velocity
, to (E.6) which holds for any velocity 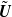 , an extra term
, an extra term 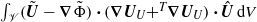 arises on the right-hand side of the latter and hence on that of (E.8). Therefore the right-hand side of (3.6) actually involves an additional contribution
arises on the right-hand side of the latter and hence on that of (E.8). Therefore the right-hand side of (3.6) actually involves an additional contribution 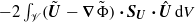 , where
, where 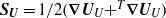 denotes the strain-rate tensor associated with the undisturbed flow field. This contribution to the force and torque results from the distortion by the underlying strain rate of the vortical velocity disturbance
denotes the strain-rate tensor associated with the undisturbed flow field. This contribution to the force and torque results from the distortion by the underlying strain rate of the vortical velocity disturbance 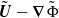 generated either by the dynamic boundary condition at the body surface
generated either by the dynamic boundary condition at the body surface 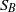 (and possibly on the wall
(and possibly on the wall 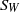 ), or/and by the vorticity
), or/and by the vorticity 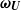 of the undisturbed flow within the core of the fluid. This extra term gives in turn rise to an additional contribution
of the undisturbed flow within the core of the fluid. This extra term gives in turn rise to an additional contribution 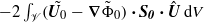 on the right-hand side of (3.13)–(3.15). This term was not present in the inviscid expressions established by Miloh (2003) because his derivation was restricted to situations in which the velocity disturbance is irrotational throughout the flow domain. This extra term does not alter the conclusions brought in the present paper for inviscid two-dimensional flows, nor those corresponding to the short-time limit of inviscid three-dimensional flows. In the limit
on the right-hand side of (3.13)–(3.15). This term was not present in the inviscid expressions established by Miloh (2003) because his derivation was restricted to situations in which the velocity disturbance is irrotational throughout the flow domain. This extra term does not alter the conclusions brought in the present paper for inviscid two-dimensional flows, nor those corresponding to the short-time limit of inviscid three-dimensional flows. In the limit 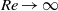 considered in the example of § 4.3, the disturbance is still irrotational outside the boundary layers that develop around the bubble and along the wall, respectively. The leading order in the vortical velocity disturbance is of
considered in the example of § 4.3, the disturbance is still irrotational outside the boundary layers that develop around the bubble and along the wall, respectively. The leading order in the vortical velocity disturbance is of 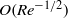 around the bubble, both in the
around the bubble, both in the 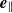 and
and 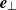 directions. Near the wall, it is of
directions. Near the wall, it is of 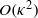 (respectively
(respectively 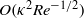 ) in the
) in the 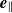 (respectively
(respectively 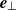 ) direction. Since the thickness of both boundary layers is of
) direction. Since the thickness of both boundary layers is of 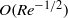 and
and 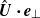 grows linearly with the distance to the wall, the extra term
grows linearly with the distance to the wall, the extra term 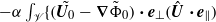
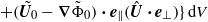 yields an
yields an 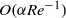 net contribution provided by the bubble boundary layer and only an
net contribution provided by the bubble boundary layer and only an 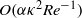 correction provided by the wall boundary layer. Hence the inviscid predictions (4.26) and (4.33) are unchanged and there is an
correction provided by the wall boundary layer. Hence the inviscid predictions (4.26) and (4.33) are unchanged and there is an 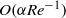 correction to the viscous drag and lift, similar in magnitude to that resulting from the term
correction to the viscous drag and lift, similar in magnitude to that resulting from the term 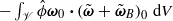 . Owing to the weak inhomogeneity assumption invoked in §§ 3.2 and 4.3, the dimensionless shear rate
. Owing to the weak inhomogeneity assumption invoked in §§ 3.2 and 4.3, the dimensionless shear rate  must be much smaller than unity for (4.26) and (4.33) to hold. Hence, in this context, the above corrections to the drag are much smaller than the leading,
must be much smaller than unity for (4.26) and (4.33) to hold. Hence, in this context, the above corrections to the drag are much smaller than the leading, 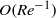 , contribution provided by the surface term
, contribution provided by the surface term 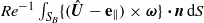 . Note that the above
. Note that the above 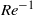 prefactor is missing on the right-hand side of (4.16) and (4.19).
prefactor is missing on the right-hand side of (4.16) and (4.19).
Information
- Type
- Corrigendum
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
This correction applies to the following article(s):
- 1
- Cited by

