Article contents
Reconsideration of spanwise rotating turbulent channel flows via resolvent analysis
Published online by Cambridge University Press: 19 December 2018
Abstract
We study the effect of spanwise rotation in turbulent channel flow at both low and high Reynolds numbers by employing the resolvent formulation proposed by McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382). Under this formulation, the nonlinear terms in the Navier–Stokes equations are regarded as a forcing that acts upon the remaining linear dynamics to generate the turbulent velocity field in response. A gain-based decomposition of the forcing–response transfer function across spectral space yields models for highly amplified flow structures, or modes. Unlike linear stability analysis, this enables targeted analyses of the effects of rotation on high-gain modes that serve as useful low-order models for dynamically important coherent structures in wall-bounded turbulent flows. The present study examines a wide range of rotation rates. A posteriori comparisons at low Reynolds number (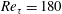 $\mathit{Re}_{\unicode[STIX]{x1D70F}}=180$) demonstrate that the resolvent formulation is able to quantitatively predict the effect of varying spanwise rotation rates on specific classes of flow structure (e.g. the near-wall cycle) as well as energy amplification across spectral space. For fixed inner-normalized rotation number, the effects of rotation at varying friction Reynolds numbers appear to be similar across spectral space, when scaled in outer units. We also consider the effects of rotation on modes with varying speed (i.e. modes that are localized in regions of varying mean shear), and provide suggestions for modelling the nonlinear forcing term.
$\mathit{Re}_{\unicode[STIX]{x1D70F}}=180$) demonstrate that the resolvent formulation is able to quantitatively predict the effect of varying spanwise rotation rates on specific classes of flow structure (e.g. the near-wall cycle) as well as energy amplification across spectral space. For fixed inner-normalized rotation number, the effects of rotation at varying friction Reynolds numbers appear to be similar across spectral space, when scaled in outer units. We also consider the effects of rotation on modes with varying speed (i.e. modes that are localized in regions of varying mean shear), and provide suggestions for modelling the nonlinear forcing term.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 2
- Cited by

