Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T19:01:21.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative periodic orbits form the backbone of turbulent pipe flow

Published online by Cambridge University Press:  06 November 2017

N. B. Budanur Open the ORCID record for N. B. Budanur [Opens in a new window] ,
K. Y. Short ,
M. Farazmand ,
A. P. Willis Open the ORCID record for A. P. Willis [Opens in a new window]  and
P. Cvitanović Open the ORCID record for P. Cvitanović [Opens in a new window]
N. B. Budanur
Affiliation:
Institute of Science and Technology (IST), Am Campus 1, 3400 Klosterneuburg, Austria Kavli Institute for Theoretical Physics, University of California Santa Barbara, Santa Barbara, CA 93106, USA
K. Y. Short
Affiliation:
School of Physics, Georgia Institute of Technology, Atlanta, GA 30332, USA
M. Farazmand
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA Kavli Institute for Theoretical Physics, University of California Santa Barbara, Santa Barbara, CA 93106, USA
A. P. Willis
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK Kavli Institute for Theoretical Physics, University of California Santa Barbara, Santa Barbara, CA 93106, USA
P. Cvitanović
Affiliation:
School of Physics, Georgia Institute of Technology, Atlanta, GA 30332, USA Kavli Institute for Theoretical Physics, University of California Santa Barbara, Santa Barbara, CA 93106, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The chaotic dynamics of low-dimensional systems, such as Lorenz or Rössler flows, is guided by the infinity of periodic orbits embedded in their strange attractors. Whether this is also the case for the infinite-dimensional dynamics of Navier–Stokes equations has long been speculated, and is a topic of ongoing study. Periodic and relative periodic solutions have been shown to be involved in transitions to turbulence. Their relevance to turbulent dynamics – specifically, whether periodic orbits play the same role in high-dimensional nonlinear systems like the Navier–Stokes equations as they do in lower-dimensional systems – is the focus of the present investigation. We perform here a detailed study of pipe flow relative periodic orbits with energies and mean dissipations close to turbulent values. We outline several approaches to reduction of the translational symmetry of the system. 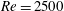We study pipe flow in a minimal computational cell at $Re=2500$, and report a library of invariant solutions found with the aid of the method of slices. Detailed study of the unstable manifolds of a sample of these solutions is consistent with the picture that relative periodic orbits are embedded in the chaotic saddle and that they guide the turbulent dynamics.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 274 - 301
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auerbach, D., Cvitanović, P., Eckmann, J.-P., Gunaratne, G. & Procaccia, I. 1987 Exploring chaotic motion through periodic orbits. Phys. Rev. Lett. 58, 2387–2389.Google Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333, 192–196.Google Scholar
Avila, M., Willis, A. P. & Hof, B. 2010 On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 646, 127–136.CrossRefGoogle Scholar
Benedicks, M. & Carleson, L. 1991 The dynamics of the Hénon map. Ann. Maths 133, 73–169.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Budanur, N. B.2015 Exact coherent structures in spatiotemporal chaos: from qualitative description to quantitative predictions. PhD thesis, School of Physics, Georgia Institute of Technology, Atlanta.Google Scholar
Budanur, N. B. & Cvitanović, P. 2017 Unstable manifolds of relative periodic orbits in the symmetry-reduced state space of the Kuramoto–Sivashinsky system. J. Stat. Phys. 167, 636–655.Google Scholar
Budanur, N. B., Cvitanović, P., Davidchack, R. L. & Siminos, E. 2015 Reduction of the SO(2) symmetry for spatially extended dynamical systems. Phys. Rev. Lett. 114, 084102.Google Scholar
Budanur, N. B. & Hof, B. 2017 Heteroclinic path to spatially localized chaos in pipe flow. J. Fluid Mech. 827, R1.Google Scholar
de Carvalho, A. & Hall, T. 2002 How to prune a horseshoe. Nonlinearity 15, R19R68.Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.Google Scholar
Cvitanović, P. 2017 Life in extreme dimensions. In Chaos: Classical and Quantum (ed. Cvitanović, P., Artuso, R., Mainieri, R., Tanner, G. & Vattay, G.). Niels Bohr Institute.Google Scholar
Cvitanović, P., Artuso, R., Mainieri, R., Tanner, G. & Vattay, G. 2017 Chaos: Classical and Quantum. Niels Bohr Institute.Google Scholar
Cvitanović, P., Borrero-Echeverry, D., Carroll, K., Robbins, B. & Siminos, E. 2012 Cartography of high-dimensional flows: a visual guide to sections and slices. Chaos 22, 047506.CrossRefGoogle ScholarPubMed
Cvitanović, P. & Gibson, J. F. 2010 Geometry of turbulence in wall-bounded shear flows: periodic orbits. Phys. Scr. T 142, 014007.Google Scholar
Cvitanović, P., Gunaratne, G. H. & Procaccia, I. 1988 Topological and metric properties of Hénon-type strange attractors. Phys. Rev. A 38, 1503–1520.Google Scholar
Dennis, D. J. C. & Sogaro, F. M. 2014 Distinct organizational states of fully developed turbulent pipe flow. Phys. Rev. Lett. 113, 234501.CrossRefGoogle ScholarPubMed
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Farazmand, M. 2016 An adjoint-based approach for finding invariant solutions of Navier–Stokes equations. J. Fluid Mech. 795, 278–312.Google Scholar
Gibson, J. F.2017 Channelflow: a spectral Navier–Stokes simulator in C++. Tech. Rep. University of New Hampshire, Channelflow.org.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Hagen, G. 1839 Über die Bewegung des Wassers in engen cylindrischen Röhren. Ann. Phys. 122, 423–442.CrossRefGoogle Scholar
Halcrow, J., Gibson, J. F., Cvitanović, P. & Viswanath, D. 2009 Heteroclinic connections in plane Couette flow. J. Fluid Mech. 621, 365–376.CrossRefGoogle Scholar
Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305, 1594–1598.Google Scholar
Hof, B., Westerweel, J., Schneider, T. M. & Eckhardt, B. 2006 Finite lifetime of turbulence in shear flows. Nature 443 (7107), 59–62.Google Scholar
Kreilos, T., Zammert, S. & Eckhardt, B. 2014 Comoving frames and symmetry-related motions in parallel shear flows. J. Fluid Mech. 751, 685–697.Google Scholar
Lax, P. D. 2002 Functional Analysis. Wiley.Google Scholar
Lin, Z., Thiffeault, J.-L. & Doering, C. R. 2011 Optimal stirring strategies for passive scalar mixing. J. Fluid Mech. 675, 465–476.Google Scholar
Mathew, G., MeziĆ, I., Grivopoulos, S., Vaidya, U. & Petzold, L. 2007 Optimal control of mixing in Stokes fluid flows. J. Fluid Mech. 580, 261–281.Google Scholar
Mellibovsky, F. & Eckhardt, B. 2012 From travelling waves to mild chaos: a supercritical bifurcation cascade in pipe flow. J. Fluid Mech. 709, 149–190.Google Scholar
Meseguer, A. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number 107 . J. Comput. Phys. 186, 178–197.CrossRefGoogle Scholar
Poiseuille, J. L. 1840 Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres. C. R. Acad. Sci. Paris 11, 961.Google Scholar
Pringle, C. C. T., Duguet, Y. & Kerswell, R. R. 2009 Highly symmetric travelling waves in pipe flow. Phil. Trans. R. Soc. Lond. A 367, 457–472.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2007 Asymmetric, helical, and mirror-symmetric traveling waves in pipe flow. Phys. Rev. Lett. 99, 074502.Google Scholar
Rowley, C. W., Kevrekidis, I. G., Marsden, J. E. & Lust, K. 2003 Reduction and reconstruction for self-similar dynamical systems. Nonlinearity 16, 1257–1275.Google Scholar
Rowley, C. W. & Marsden, J. E. 2000 Reconstruction equations and the Karhunen–Loève expansion for systems with symmetry. Physica D 142, 1–19.Google Scholar
Short, K. Y. & Willis, A. P.2017 Bifurcation structure of relative periodic orbits in pipe flow (in preparation).Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Cvitanović, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.Google Scholar
Willis, A. P., Short, K. Y. & Cvitanović, P. 2016 Symmetry reduction in high dimensions, illustrated in a turbulent pipe. Phys. Rev. E 93, 022204.Google Scholar