1 Introduction
Understanding the surface-tension-driven break-up of liquid cylinders and their subsequent disintegration into droplets is crucial to a range of technologies such as ink-jet printing (Basaran, Gao & Bhat Reference Basaran, Gao and Bhat2013), fibre manufacture (Shabahang et al.
Reference Shabahang, Kaufman, Deng and Abouraddy2011) and drug delivery (Mitragotri Reference Mitragotri2006). The classical theoretical results are due to Plateau (Reference Plateau1873), who showed that a cylinder of radius
![]() $r_{0}$
is unstable to sufficiently long wavelength disturbances
$r_{0}$
is unstable to sufficiently long wavelength disturbances
![]() $\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{crit}=2\unicode[STIX]{x03C0}r_{0}$
and Rayleigh (Reference Rayleigh1878), who conducted a linear stability analysis of the inviscid dynamics to find a fastest growing mode with wavelength
$\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{crit}=2\unicode[STIX]{x03C0}r_{0}$
and Rayleigh (Reference Rayleigh1878), who conducted a linear stability analysis of the inviscid dynamics to find a fastest growing mode with wavelength
![]() $\unicode[STIX]{x1D706}_{max}=9.01r_{0}$
(or wavenumber
$\unicode[STIX]{x1D706}_{max}=9.01r_{0}$
(or wavenumber
![]() $k_{max}=0.697/r_{0}$
). The Rayleigh–Plateau (RP) theoretical framework has been subject to numerous generalisations (e.g. Rayleigh (Reference Rayleigh1892), Tomotika (Reference Tomotika1935)) and accurately describes macroscopic experiments (Eggers & Villermaux Reference Eggers and Villermaux2008).
$k_{max}=0.697/r_{0}$
). The Rayleigh–Plateau (RP) theoretical framework has been subject to numerous generalisations (e.g. Rayleigh (Reference Rayleigh1892), Tomotika (Reference Tomotika1935)) and accurately describes macroscopic experiments (Eggers & Villermaux Reference Eggers and Villermaux2008).
With an increasing interest in micro and nano fluid dynamics, driven by emerging technologies in these domains (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004), there has been cause to reassess the validity of classical analyses at smaller scales and question the absolute truth of long-held intuition. For liquid flows, molecular dynamics (MD) allows one to perform nanoscale ‘experiments’ and these have been shown to qualitatively reproduce RP-like instability (Koplik & Banavar Reference Koplik and Banavar1993). However, MD studies of long cylinders (Kawano Reference Kawano1998; Gopan & Sathian Reference Gopan and Sathian2014) have been unable to conclusively (i.e. quantitatively) validate classical theory.
It is well recognised that although
![]() $k_{max}$
can give a first approximation of the drop size formed, the actual break-up is a nonlinear asymmetric ‘universal’ solution (Eggers Reference Eggers1993) that resembles a drop connected to a thin cylinder. Interestingly, at the nanoscale, MD showed instead the emergence of a new double-cone break-up profile (Moseler & Landman Reference Moseler and Landman2000), generated by the presence of thermal fluctuations of molecules whose effects are negligible for standard liquids at the macroscale. This behaviour was described using a ‘stochastic lubrication equation’ (SLE) derived by applying the lubrication approximation to the equations of fluctuating hydrodynamics (Landau, Lifshits & Pitaevskii Reference Landau, Lifshits and Pitaevskii1980). The importance of the fluctuations has been confirmed by experiments (Hennequin et al.
Reference Hennequin, Aarts, van der Wiel, Wegdam, Eggers, Lekkerkerker and Bonn2006; Petit et al.
Reference Petit, Rivière, Kellay and Delville2012), analytical models (Eggers Reference Eggers2002) and subsequent MD (Choi, Kim & Kim Reference Choi, Kim and Kim2006; Kang & Landman Reference Kang and Landman2007).
$k_{max}$
can give a first approximation of the drop size formed, the actual break-up is a nonlinear asymmetric ‘universal’ solution (Eggers Reference Eggers1993) that resembles a drop connected to a thin cylinder. Interestingly, at the nanoscale, MD showed instead the emergence of a new double-cone break-up profile (Moseler & Landman Reference Moseler and Landman2000), generated by the presence of thermal fluctuations of molecules whose effects are negligible for standard liquids at the macroscale. This behaviour was described using a ‘stochastic lubrication equation’ (SLE) derived by applying the lubrication approximation to the equations of fluctuating hydrodynamics (Landau, Lifshits & Pitaevskii Reference Landau, Lifshits and Pitaevskii1980). The importance of the fluctuations has been confirmed by experiments (Hennequin et al.
Reference Hennequin, Aarts, van der Wiel, Wegdam, Eggers, Lekkerkerker and Bonn2006; Petit et al.
Reference Petit, Rivière, Kellay and Delville2012), analytical models (Eggers Reference Eggers2002) and subsequent MD (Choi, Kim & Kim Reference Choi, Kim and Kim2006; Kang & Landman Reference Kang and Landman2007).
Remarkably, despite failures to match classical RP theory to MD and a long recognition that ‘fluctuations substantially distort the shape of the cylinder’ (Koplik & Banavar Reference Koplik and Banavar1993), no one has considered how the RP instability mechanism is modified in the presence of thermal fluctuations. This is despite recognition of their importance to enhancing instabilities in thin film flows (Grün, Mecke & Rauscher Reference Grün, Mecke and Rauscher2006; Diez, González & Fernández Reference Diez, González and Fernández2016). Note, the focus of this work is on how thermal fluctuations affect stability, which is a related but distinct question to how thermal fluctuations affect break-up, as studied in Moseler & Landman (Reference Moseler and Landman2000).
In the next section, we develop an SLE-RP framework for incorporating fluctuations into the stability analysis of liquid cylinders at the nanoscale. The MD simulation method is introduced in § 3 to validate the SLE-RP. Results in § 4 show that the SLE-RP allows us to identify deviations from the classical picture, most notably a loss of the clear-cut Plateau stability criterion and very significant modifications of
![]() $k_{max}$
.
$k_{max}$
.
2 Mathematical modelling
2.1 Stochastic lubrication equation
Consider a cylindrical polar coordinate system (figure 1), with
![]() $z$
-axis along the centre line of an axisymmetric initially cylindrical liquid volume of length
$z$
-axis along the centre line of an axisymmetric initially cylindrical liquid volume of length
![]() $L$
and radius
$L$
and radius
![]() $r_{0}$
. In the lubrication approximation, the dynamics is described by the radius of the cylinder
$r_{0}$
. In the lubrication approximation, the dynamics is described by the radius of the cylinder
![]() $r=h(z,t)$
and the axial velocity
$r=h(z,t)$
and the axial velocity
![]() $u(z,t)$
, so that the SLE (Moseler & Landman Reference Moseler and Landman2000) is given by
$u(z,t)$
, so that the SLE (Moseler & Landman Reference Moseler and Landman2000) is given by
with the full Laplace pressure retained
and primes denoting differentiation with respect to
![]() $z$
. In these equations,
$z$
. In these equations,
![]() $\unicode[STIX]{x1D708}$
is the liquid’s kinematic viscosity,
$\unicode[STIX]{x1D708}$
is the liquid’s kinematic viscosity,
![]() $\unicode[STIX]{x1D70C}$
is its density,
$\unicode[STIX]{x1D70C}$
is its density,
![]() $\unicode[STIX]{x1D6FE}$
is the surface-tension coefficient and
$\unicode[STIX]{x1D6FE}$
is the surface-tension coefficient and
![]() ${\mathcal{N}}$
denotes a standard Gaussian (white) random variable, capturing the thermal fluctuation effects, where
${\mathcal{N}}$
denotes a standard Gaussian (white) random variable, capturing the thermal fluctuation effects, where
![]() $A=\sqrt{6k_{B}T\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D70C}\unicode[STIX]{x03C0})}$
is a dimensional parameter,
$A=\sqrt{6k_{B}T\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D70C}\unicode[STIX]{x03C0})}$
is a dimensional parameter,
![]() $k_{B}$
is the Boltzmann constant and
$k_{B}$
is the Boltzmann constant and
![]() $T$
is the liquid temperature. If there are no fluctuations (i.e.
$T$
is the liquid temperature. If there are no fluctuations (i.e.
![]() $A=0$
) the classical lubrication equations (LE) (Eggers & Dupont Reference Eggers and Dupont1994) are recovered.
$A=0$
) the classical lubrication equations (LE) (Eggers & Dupont Reference Eggers and Dupont1994) are recovered.

Figure 1. Schematic of the cylinder instability.
2.2 Stability analysis
For the linear stability analysis, we take
![]() $h(z,t)=r_{0}[1+\hat{r}(z,t)]$
, with
$h(z,t)=r_{0}[1+\hat{r}(z,t)]$
, with
![]() $\hat{r}(z,t)\ll 1$
a dimensionless perturbation. Substituting this into the SLE and linearising gives
$\hat{r}(z,t)\ll 1$
a dimensionless perturbation. Substituting this into the SLE and linearising gives
Note, this linearisation also implies an extent to the strength of fluctuations, which we will discuss later. A finite Fourier transform is applied to (2.4) to obtain
where
![]() $\unicode[STIX]{x1D6FC}=3\unicode[STIX]{x1D710}k^{2}$
and
$\unicode[STIX]{x1D6FC}=3\unicode[STIX]{x1D710}k^{2}$
and
![]() $\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FE}/2\unicode[STIX]{x1D70C})(r_{0}k^{4}-(k^{2}/r_{0}))$
and the transformed variables are defined as follows:
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D6FE}/2\unicode[STIX]{x1D70C})(r_{0}k^{4}-(k^{2}/r_{0}))$
and the transformed variables are defined as follows:
The solution of (2.5) is linearly decomposed into two parts:
The first part is the solution to the homogenous form of (2.5) (i.e. with
![]() $A=0$
) with some stationary initial disturbance (i.e.
$A=0$
) with some stationary initial disturbance (i.e.
![]() $R=R_{i}$
and
$R=R_{i}$
and
![]() $\text{d}R/\text{d}t=0$
at
$\text{d}R/\text{d}t=0$
at
![]() $t=0$
). The solution to the homogeneous ordinary differential equation is straightforward to obtain:
$t=0$
). The solution to the homogeneous ordinary differential equation is straightforward to obtain:
where
and characteristic flow scales for time
![]() $\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70C}r_{0}^{3}/\unicode[STIX]{x1D6FE})^{1/2}$
and length
$\unicode[STIX]{x1D70F}=(\unicode[STIX]{x1D70C}r_{0}^{3}/\unicode[STIX]{x1D6FE})^{1/2}$
and length
![]() $\ell _{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}/\unicode[STIX]{x1D6FE}$
have been introduced. This is a solution to the standard lubrication equations (there is no fluctuating component), and is thus denoted
$\ell _{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}^{2}/\unicode[STIX]{x1D6FE}$
have been introduced. This is a solution to the standard lubrication equations (there is no fluctuating component), and is thus denoted
![]() $R_{LE}$
in (2.7). Note, for the rest of this paper, the initial modal disturbance
$R_{LE}$
in (2.7). Note, for the rest of this paper, the initial modal disturbance
![]() $R_{i}$
is treated as a complex random variable with zero mean.
$R_{i}$
is treated as a complex random variable with zero mean.
The second component of the solution arises from solving the full form of (2.5) with zero initial disturbance; this part of the solution is solely due to fluctuations, and is thus denoted
![]() $R_{fluc}$
. This is obtained by the homogeneous equation’s impulse response,
$R_{fluc}$
. This is obtained by the homogeneous equation’s impulse response,
which due to the linear, time-invariant nature of the system, allows us to write
The modal amplitude
![]() $R\,(=R_{LE}+R_{fluc})$
is a complex random variable, with zero mean. Note,
$R\,(=R_{LE}+R_{fluc})$
is a complex random variable, with zero mean. Note,
![]() $R_{LE}$
is also random as it develops from a random initial condition, but is uncorrelated with
$R_{LE}$
is also random as it develops from a random initial condition, but is uncorrelated with
![]() $R_{fluc}$
(both have zero mean). So, in order to obtain information on how disturbances associated with each wavenumber develop in time, allowing the identification of unstable and fastest growing modes, the root mean square (r.m.s.) of
$R_{fluc}$
(both have zero mean). So, in order to obtain information on how disturbances associated with each wavenumber develop in time, allowing the identification of unstable and fastest growing modes, the root mean square (r.m.s.) of
![]() $|R|$
is sought (equivalent to the standard deviation of
$|R|$
is sought (equivalent to the standard deviation of
![]() $|R|$
):
$|R|$
):
where, from (2.8),
and since
![]() $N$
is uncorrelated Gaussian white noise, and the variance of the norm of the white noise
$N$
is uncorrelated Gaussian white noise, and the variance of the norm of the white noise
![]() $\overline{|N|^{2}}=L$
, equations (2.10) and (2.11) combine to give:
$\overline{|N|^{2}}=L$
, equations (2.10) and (2.11) combine to give:
 $$\begin{eqnarray}\displaystyle \overline{|R_{fluc}|^{2}} & = & \displaystyle \left(\frac{Ak^{2}}{2r_{0}}\right)^{2}\overline{\left|\int _{0}^{t}N(k,t-{\mathcal{T}})H(k,{\mathcal{T}})\,\text{d}{\mathcal{T}}\right|^{2}},\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{Ak^{2}}{2r_{0}}\right)^{2}\left(\int _{0}^{t}\overline{|N(k,t-{\mathcal{T}})|^{2}}H(k,{\mathcal{T}})^{2}\,\text{d}{\mathcal{T}}\right),\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{Ak^{2}}{2r_{0}}\right)^{2}L\int _{0}^{t}H^{2}\,\text{d}{\mathcal{T}},\nonumber\\ \displaystyle & = & \displaystyle \ell _{fluc}^{2}b\frac{(a^{2}-c^{2})-a^{2}\cosh (ct/\unicode[STIX]{x1D70F})-ac\sinh (ct/\unicode[STIX]{x1D70F})+c^{2}\text{e}^{at/\unicode[STIX]{x1D70F}}}{ac^{2}(a^{2}-c^{2})\text{e}^{at/\unicode[STIX]{x1D70F}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{|R_{fluc}|^{2}} & = & \displaystyle \left(\frac{Ak^{2}}{2r_{0}}\right)^{2}\overline{\left|\int _{0}^{t}N(k,t-{\mathcal{T}})H(k,{\mathcal{T}})\,\text{d}{\mathcal{T}}\right|^{2}},\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{Ak^{2}}{2r_{0}}\right)^{2}\left(\int _{0}^{t}\overline{|N(k,t-{\mathcal{T}})|^{2}}H(k,{\mathcal{T}})^{2}\,\text{d}{\mathcal{T}}\right),\nonumber\\ \displaystyle & = & \displaystyle \left(\frac{Ak^{2}}{2r_{0}}\right)^{2}L\int _{0}^{t}H^{2}\,\text{d}{\mathcal{T}},\nonumber\\ \displaystyle & = & \displaystyle \ell _{fluc}^{2}b\frac{(a^{2}-c^{2})-a^{2}\cosh (ct/\unicode[STIX]{x1D70F})-ac\sinh (ct/\unicode[STIX]{x1D70F})+c^{2}\text{e}^{at/\unicode[STIX]{x1D70F}}}{ac^{2}(a^{2}-c^{2})\text{e}^{at/\unicode[STIX]{x1D70F}}},\end{eqnarray}$$
where non-dimensional
![]() $b=(3/\unicode[STIX]{x03C0})(L/r_{0})(kr_{0})^{4}(\ell _{\unicode[STIX]{x1D708}}/r_{0})^{1/2}$
, and the thermal capillary length
$b=(3/\unicode[STIX]{x03C0})(L/r_{0})(kr_{0})^{4}(\ell _{\unicode[STIX]{x1D708}}/r_{0})^{1/2}$
, and the thermal capillary length
![]() $\ell _{fluc}=(k_{B}T/\unicode[STIX]{x1D6FE})^{1/2}$
gives the characteristic length scale of the fluctuations.
$\ell _{fluc}=(k_{B}T/\unicode[STIX]{x1D6FE})^{1/2}$
gives the characteristic length scale of the fluctuations.
2.3 Convergence to the classical model
From (2.12), fluctuations can be seen to be negligible when the thermal capillary length is very much shorter than the initial modal amplitude; i.e.
![]() $R\rightarrow R_{LE}$
as
$R\rightarrow R_{LE}$
as
![]() $\ell _{fluc}^{2}/\overline{|R_{i}|^{2}}\rightarrow 0$
. We refer to this classical limit as the LE-RP model (as distinct from the SLE-RP). In order to compare with standard stability analysis, we want to find the fastest growing mode at a long time after any initial disturbance. As such we take
$\ell _{fluc}^{2}/\overline{|R_{i}|^{2}}\rightarrow 0$
. We refer to this classical limit as the LE-RP model (as distinct from the SLE-RP). In order to compare with standard stability analysis, we want to find the fastest growing mode at a long time after any initial disturbance. As such we take
![]() $t\rightarrow \infty$
to give:
$t\rightarrow \infty$
to give:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \overline{|R_{LE}|^{2}}\rightarrow \overline{|R_{i}|^{2}}\text{e}^{(c-a)t/\unicode[STIX]{x1D70F}}\left(\frac{c+a}{2c}\right)^{2},\\ \displaystyle \overline{|R_{fluc}|^{2}}\rightarrow \frac{\ell _{fluc}^{2}\,b}{2ac^{2}(a^{2}-c^{2})}[2c^{2}-\text{e}^{(c-a)t/\unicode[STIX]{x1D70F}}(a^{2}+ac)],\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \overline{|R_{LE}|^{2}}\rightarrow \overline{|R_{i}|^{2}}\text{e}^{(c-a)t/\unicode[STIX]{x1D70F}}\left(\frac{c+a}{2c}\right)^{2},\\ \displaystyle \overline{|R_{fluc}|^{2}}\rightarrow \frac{\ell _{fluc}^{2}\,b}{2ac^{2}(a^{2}-c^{2})}[2c^{2}-\text{e}^{(c-a)t/\unicode[STIX]{x1D70F}}(a^{2}+ac)],\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with
![]() $c-a\geqslant 0$
for
$c-a\geqslant 0$
for
![]() $kr_{0}\leqslant 1$
(which is the case as
$kr_{0}\leqslant 1$
(which is the case as
![]() $t\rightarrow \infty$
). Therefore, a functional form of (2.12) is:
$t\rightarrow \infty$
). Therefore, a functional form of (2.12) is:
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{G}}(k)=(c-a)/\unicode[STIX]{x1D70F},\\ \displaystyle {\mathcal{F}}_{1}(k)=\overline{|R_{i}|^{2}}\left(\frac{c+a}{2c}\right)^{2}+\frac{\ell _{fluc}^{2}\,b}{2c^{2}(c-a)},\\ \displaystyle {\mathcal{F}}_{2}(k)=\frac{\ell _{fluc}^{2}\,b}{a(a^{2}-c^{2})}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{G}}(k)=(c-a)/\unicode[STIX]{x1D70F},\\ \displaystyle {\mathcal{F}}_{1}(k)=\overline{|R_{i}|^{2}}\left(\frac{c+a}{2c}\right)^{2}+\frac{\ell _{fluc}^{2}\,b}{2c^{2}(c-a)},\\ \displaystyle {\mathcal{F}}_{2}(k)=\frac{\ell _{fluc}^{2}\,b}{a(a^{2}-c^{2})}.\end{array}\right\}\end{eqnarray}$$
In order to find the maximum of
![]() ${\mathcal{R}}(k,t)$
, which defines the fastest growing mode
${\mathcal{R}}(k,t)$
, which defines the fastest growing mode
![]() $k=k_{max}$
, we calculate the derivative of (2.16) with respect to
$k=k_{max}$
, we calculate the derivative of (2.16) with respect to
![]() $k$
to obtain
$k$
to obtain
and set
![]() $\unicode[STIX]{x2202}{\mathcal{R}}/\unicode[STIX]{x2202}k=0$
. As
$\unicode[STIX]{x2202}{\mathcal{R}}/\unicode[STIX]{x2202}k=0$
. As
![]() $1/t$
and
$1/t$
and
![]() $\text{e}^{-{\mathcal{G}}t}$
vanish as
$\text{e}^{-{\mathcal{G}}t}$
vanish as
![]() $t\rightarrow \infty$
, and
$t\rightarrow \infty$
, and
![]() ${\mathcal{F}}_{1}(k_{max})\neq 0$
, the equation for determining
${\mathcal{F}}_{1}(k_{max})\neq 0$
, the equation for determining
![]() $k_{max}$
is simply
$k_{max}$
is simply
which is the same as found by Eggers & Dupont (Reference Eggers and Dupont1994) who neglected fluctuations entirely. However, as break-up occurs in a finite time, both terms in (2.12) could play a role in determining
![]() $k_{max}$
at any instant, with the second term becoming more important as
$k_{max}$
at any instant, with the second term becoming more important as
![]() $\ell _{fluc}^{2}/\overline{|R_{i}|^{2}}$
increases (all else being constant).
$\ell _{fluc}^{2}/\overline{|R_{i}|^{2}}$
increases (all else being constant).
3 Simulations
To test our hypothesis, MD simulations (in figure 2) are performed in LAMMPS (Plimpton Reference Plimpton1995) on long cylinders
![]() $L/r_{0}=160$
of three different radii: Cylinder 1 (
$L/r_{0}=160$
of three different radii: Cylinder 1 (
![]() $r_{0}=5.76$
nm,
$r_{0}=5.76$
nm,
![]() $2.1\times 10^{6}$
particles), Cylinder 2 (
$2.1\times 10^{6}$
particles), Cylinder 2 (
![]() $r_{0}=2.88$
nm,
$r_{0}=2.88$
nm,
![]() $2.8\times 10^{5}$
particles) and Cylinder 3 (
$2.8\times 10^{5}$
particles) and Cylinder 3 (
![]() $r_{0}=$
1.44 nm,
$r_{0}=$
1.44 nm,
![]() $4.6\times 10^{4}$
particles). The simulation box (
$4.6\times 10^{4}$
particles). The simulation box (
![]() $57$
nm
$57$
nm
![]() $\times$
$\times$
![]() $57$
nm
$57$
nm
![]() $\times \,L$
in the
$\times \,L$
in the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
directions, respectively) has periodic boundary conditions imposed in all directions and is filled with Lennard-Jones (LJ) fluid whose atomic interactions are modelled using the standard 12-6 pair potential with the cutoff distance
$z$
directions, respectively) has periodic boundary conditions imposed in all directions and is filled with Lennard-Jones (LJ) fluid whose atomic interactions are modelled using the standard 12-6 pair potential with the cutoff distance
![]() $5.5\unicode[STIX]{x1D70E}$
; interaction potentials for argon have been employed (Lee, Barker & Pound Reference Lee, Barker and Pound1974). The initial configuration is created from equilibrium simulations of separate liquid-only and vapour-only systems (using a canonical ensemble (NVT) with a Nosé–Hoover thermostat) with respective densities of
$5.5\unicode[STIX]{x1D70E}$
; interaction potentials for argon have been employed (Lee, Barker & Pound Reference Lee, Barker and Pound1974). The initial configuration is created from equilibrium simulations of separate liquid-only and vapour-only systems (using a canonical ensemble (NVT) with a Nosé–Hoover thermostat) with respective densities of
![]() $1398~\text{kg}~\text{m}^{-3}$
and
$1398~\text{kg}~\text{m}^{-3}$
and
![]() $3.22~\text{kg}~\text{m}^{-3}$
, which correspond to the saturated liquid and vapour densities at a temperature of 84.09 K (Fernandez, Vrabec & Hasse Reference Fernandez, Vrabec and Hasse2004). The same ensemble and thermostat is used for the full simulations.
$3.22~\text{kg}~\text{m}^{-3}$
, which correspond to the saturated liquid and vapour densities at a temperature of 84.09 K (Fernandez, Vrabec & Hasse Reference Fernandez, Vrabec and Hasse2004). The same ensemble and thermostat is used for the full simulations.
The kinematic viscosity is found using the Green–Kubo method (Green Reference Green1954; Kubo Reference Kubo1957) to be
![]() $\unicode[STIX]{x1D708}=1.76\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
. This technique calculates dynamic viscosity by integration of the time-autocorrelation function of the off-diagonal elements of the pressure tensor
$\unicode[STIX]{x1D708}=1.76\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
. This technique calculates dynamic viscosity by integration of the time-autocorrelation function of the off-diagonal elements of the pressure tensor
![]() $P_{ij}$
so that
$P_{ij}$
so that
where the pressure tensor is obtained using the definition of Kirkwood & Buff (Reference Kirkwood and Buff1949) and the brackets indicate the expectation value.
![]() $V_{bulk}$
represents the volume of the bulk fluid under consideration. The surface tension is calculated from the profiles of the components of the pressure tensor in a simple liquid–vapour system (Trokhymchuk & Alejandre Reference Trokhymchuk and Alejandre1999):
$V_{bulk}$
represents the volume of the bulk fluid under consideration. The surface tension is calculated from the profiles of the components of the pressure tensor in a simple liquid–vapour system (Trokhymchuk & Alejandre Reference Trokhymchuk and Alejandre1999):
where
![]() $L_{z}$
is the length of the MD domain, and subscripts ‘
$L_{z}$
is the length of the MD domain, and subscripts ‘
![]() $n$
’ and ‘
$n$
’ and ‘
![]() $t$
’ denote normal and tangential components, respectively. We have found that to obtain results that are close to experimental data (Trokhymchuk & Alejandre Reference Trokhymchuk and Alejandre1999), a cutoff distance significantly larger than the popular choice of 2.5
$t$
’ denote normal and tangential components, respectively. We have found that to obtain results that are close to experimental data (Trokhymchuk & Alejandre Reference Trokhymchuk and Alejandre1999), a cutoff distance significantly larger than the popular choice of 2.5
![]() $\unicode[STIX]{x1D70E}$
is required; a choice of 5.5
$\unicode[STIX]{x1D70E}$
is required; a choice of 5.5
![]() $\unicode[STIX]{x1D70E}$
(used throughout) has proved to be sufficiently accurate. Finally, we have
$\unicode[STIX]{x1D70E}$
(used throughout) has proved to be sufficiently accurate. Finally, we have
![]() $\unicode[STIX]{x1D6FE}=1.42\times 10^{-2}~\text{N}~\text{m}^{-1}$
and
$\unicode[STIX]{x1D6FE}=1.42\times 10^{-2}~\text{N}~\text{m}^{-1}$
and
![]() $\ell _{fluc}=0.2859$
nm.
$\ell _{fluc}=0.2859$
nm.

Figure 2. Molecular dynamics simulation of the Rayleigh–Plateau instability showing a liquid cylinder (Cylinder 1) breaking into droplets.
4 Results and discussion
To gather statistics, multiple independent MD simulations (realisations) (Cylinder 1:
![]() $30$
, Cylinder 2:
$30$
, Cylinder 2:
![]() $45$
and Cylinder 3:
$45$
and Cylinder 3:
![]() $100$
) are performed. For each realisation, a discrete Fourier transform of the interface position (which is extracted from axially distributed annular bins based on a threshold density) is performed and then an ensemble average at each time allows us to produce the results shown in figure 3 (dashed lines) and figure 4 (red dots). Using the initial conditions from MD to extract
$100$
) are performed. For each realisation, a discrete Fourier transform of the interface position (which is extracted from axially distributed annular bins based on a threshold density) is performed and then an ensemble average at each time allows us to produce the results shown in figure 3 (dashed lines) and figure 4 (red dots). Using the initial conditions from MD to extract
![]() $\overline{|R_{i}|^{2}}$
, remarkably good agreement with the SLE-RP is obtained, giving us confidence that our approach captures the essential physics.
$\overline{|R_{i}|^{2}}$
, remarkably good agreement with the SLE-RP is obtained, giving us confidence that our approach captures the essential physics.
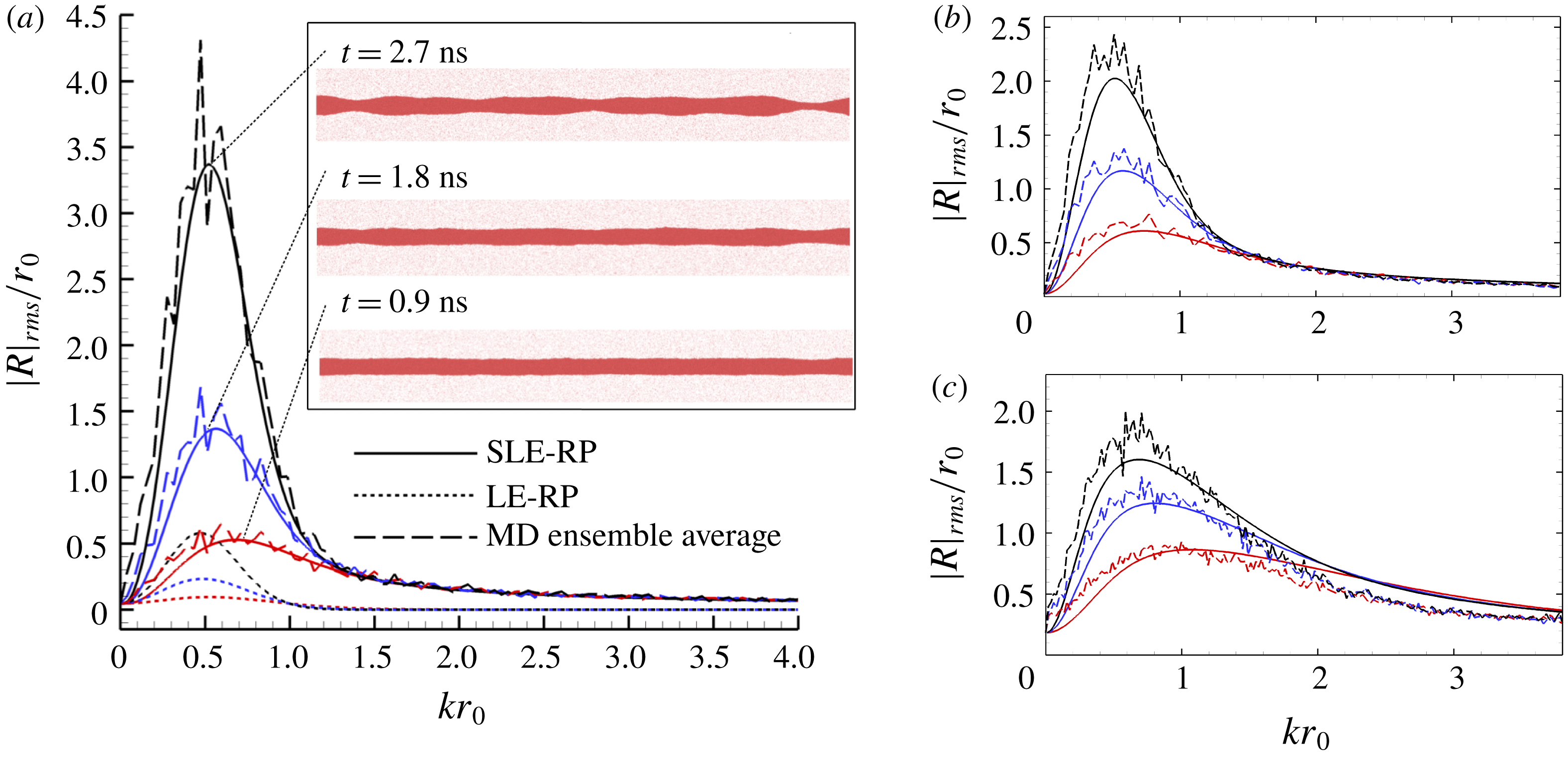
Figure 3. The r.m.s. of dimensionless modal amplitude versus dimensionless wavenumber; a comparison of ensemble-averaged MD data (dashed lines) and (2.12) (solid lines) at various time instances. (a) Results of Cylinder 1; the inset shows selected MD realisations; (b) Results of Cylinder 2, the three timesteps are:
![]() $0.23$
(red),
$0.23$
(red),
![]() $0.47$
(blue),
$0.47$
(blue),
![]() $0.70$
(black)/ns; (c) Results of Cylinder 3, the three timesteps are:
$0.70$
(black)/ns; (c) Results of Cylinder 3, the three timesteps are:
![]() $0.062$
(red),
$0.062$
(red),
![]() $0.125$
(blue),
$0.125$
(blue),
![]() $0.100$
(black)/ns.
$0.100$
(black)/ns.
The MD results in figure 3 illustrate that there exists a modal distribution which varies with time, becoming sharper as it evolves. Extracting
![]() $k_{max}$
from these data yields the plots in figure 4, which confirm that
$k_{max}$
from these data yields the plots in figure 4, which confirm that
![]() $k_{max}$
tends to the Eggers & Dupont result as
$k_{max}$
tends to the Eggers & Dupont result as
![]() $t\rightarrow \infty$
. However, figure 4 also shows that
$t\rightarrow \infty$
. However, figure 4 also shows that
![]() $k_{max}$
at the average break-up time (which ultimately determines drop size) is consistently overpredicted by Rayleigh’s inviscid result, as seen in previous MD, and underpredicted by the Eggers & Dupont model (valid across all values of viscosity) – particularly for the smallest radius (Cylinder 3) where
$k_{max}$
at the average break-up time (which ultimately determines drop size) is consistently overpredicted by Rayleigh’s inviscid result, as seen in previous MD, and underpredicted by the Eggers & Dupont model (valid across all values of viscosity) – particularly for the smallest radius (Cylinder 3) where
![]() $k_{max}=0.52/r_{0}$
in the MD and
$k_{max}=0.52/r_{0}$
in the MD and
![]() $k_{max}=0.35/r_{0}$
from Eggers & Dupont. The modal analysis based purely on the LE-RP also underpredicts the MD data and fails to exhibit the dominant short wavelength modes observed at early times. In contrast, the SLE-RP curves in both figures 3 and 4 give excellent agreement with the MD and underline the critical role of thermal fluctuations in the instability mechanism at the nanoscale. Note, however, that the agreement between the SLE-RP and the MD is less good for the smallest cylinder. This can potentially be explained by the decreasing validity with decreasing scale of the weak-fluctuation assumption in our SLE-RP analysis. Crudely,
$k_{max}=0.35/r_{0}$
from Eggers & Dupont. The modal analysis based purely on the LE-RP also underpredicts the MD data and fails to exhibit the dominant short wavelength modes observed at early times. In contrast, the SLE-RP curves in both figures 3 and 4 give excellent agreement with the MD and underline the critical role of thermal fluctuations in the instability mechanism at the nanoscale. Note, however, that the agreement between the SLE-RP and the MD is less good for the smallest cylinder. This can potentially be explained by the decreasing validity with decreasing scale of the weak-fluctuation assumption in our SLE-RP analysis. Crudely,
![]() $l_{fluc}/r_{0}\ll 1$
for the linear analysis to be valid. Here,
$l_{fluc}/r_{0}\ll 1$
for the linear analysis to be valid. Here,
![]() $l_{fluc}/r_{0}=0.05$
, 0.1 and 0.2, for the three cylinders, listed largest to smallest.
$l_{fluc}/r_{0}=0.05$
, 0.1 and 0.2, for the three cylinders, listed largest to smallest.

Figure 4. Evolution in time
![]() $t$
of the wavenumber with greatest amplitude (
$t$
of the wavenumber with greatest amplitude (
![]() $k_{max}$
) for (a) Cylinder 1 (b) Cylinder 2 and (c) Cylinder 3. Red dots and solid lines are the maximum predicted by MD (interpolation) and the SLE-RP respectively. Average break-up time,
$k_{max}$
) for (a) Cylinder 1 (b) Cylinder 2 and (c) Cylinder 3. Red dots and solid lines are the maximum predicted by MD (interpolation) and the SLE-RP respectively. Average break-up time,
![]() $\bar{t}_{b}$
, is obtained from the MD data.
$\bar{t}_{b}$
, is obtained from the MD data.
Intriguingly, the early time behaviour in figure 4 indicates that
![]() $k_{max}r_{0}$
can be greater than unity, violating the classical stability criterion of Plateau. Therefore, it seems possible that ‘fat’ cylinders, whose length is below the classical critical stability (
$k_{max}r_{0}$
can be greater than unity, violating the classical stability criterion of Plateau. Therefore, it seems possible that ‘fat’ cylinders, whose length is below the classical critical stability (
![]() $L<L_{crit}=2\unicode[STIX]{x03C0}r_{0}$
), may be unstable in the presence of fluctuations. To test the hypothesis, we consider (2.12) at the critical point, i.e. when
$L<L_{crit}=2\unicode[STIX]{x03C0}r_{0}$
), may be unstable in the presence of fluctuations. To test the hypothesis, we consider (2.12) at the critical point, i.e. when
![]() $kr_{0}=1$
to obtain
$kr_{0}=1$
to obtain
Notably the contribution from LE equations (the first term on the right-hand side of (4.1)) is a constant; so, according to the classical model, the initial disturbance neither decays or grows. Hence, it is critically stable. However, the second term (due purely to fluctuations) grows in proportion to
![]() $t$
as
$t$
as
![]() $t\rightarrow \infty$
, giving a potential mechanism for break-up. This suggests that cylinders of the critical length, and perhaps shorter, are likely to be unstable at the nanoscale. To verify these conclusions, we perform a further series of MD experiments for cylinders of two radii (
$t\rightarrow \infty$
, giving a potential mechanism for break-up. This suggests that cylinders of the critical length, and perhaps shorter, are likely to be unstable at the nanoscale. To verify these conclusions, we perform a further series of MD experiments for cylinders of two radii (
![]() $r_{0}=1.44,2.88$
nm) slightly shorter than the critical length
$r_{0}=1.44,2.88$
nm) slightly shorter than the critical length
![]() $L_{crit}$
so that all classically unstable (long) wavelengths are suppressed by the domain size. This has been performed using two different flow configurations, one in which periodic boundary conditions are applied and the other in which the liquid cylinder is bounded at each end by a solid wall.
$L_{crit}$
so that all classically unstable (long) wavelengths are suppressed by the domain size. This has been performed using two different flow configurations, one in which periodic boundary conditions are applied and the other in which the liquid cylinder is bounded at each end by a solid wall.
The four cases in figure 5 (cylinders of two radii for each end condition) all have length
![]() $L=6r_{0}<L_{crit}$
, and thus satisfy Plateau’s stability criterion. However, all break-up in a finite time, supporting our conclusion from SLE-RP that fat cylinders can indeed become unstable at the nanoscale. Notably, the break-up shapes resemble the double-cone profiles first observed by Moseler & Landman (Reference Moseler and Landman2000).
$L=6r_{0}<L_{crit}$
, and thus satisfy Plateau’s stability criterion. However, all break-up in a finite time, supporting our conclusion from SLE-RP that fat cylinders can indeed become unstable at the nanoscale. Notably, the break-up shapes resemble the double-cone profiles first observed by Moseler & Landman (Reference Moseler and Landman2000).
Having established the possibility of violating the Plateau criterion at the nanoscale, in figure 6 we show the average break-up time of such cylinders using 50 independent MD simulations for each data point (the standard deviation is indicated). There are two intuitive observations: (i) for the smaller radius cylinder, the break-up (which is partly or wholly due to fluctuations) occurs significantly faster than for the larger radius cylinder; (ii) as the aspect ratio of the cylinder decreases (i.e. becomes fatter) and crosses the classical stability limit (
![]() $L_{crit}/L>1$
), the average break-up time increases dramatically, and so does the variance in the measured times. This is because, at lower aspect ratios, the stabilising effect of surface tension becomes stronger and one has to wait longer (on average) for the ‘perfect storm’ of fluctuations to arrive that will overcome these and rupture the cylinder. This could explain why previous MD (Min & Wong Reference Min and Wong2006) appears to support the classical criterion: to violate the Plateau stability one must either be close to
$L_{crit}/L>1$
), the average break-up time increases dramatically, and so does the variance in the measured times. This is because, at lower aspect ratios, the stabilising effect of surface tension becomes stronger and one has to wait longer (on average) for the ‘perfect storm’ of fluctuations to arrive that will overcome these and rupture the cylinder. This could explain why previous MD (Min & Wong Reference Min and Wong2006) appears to support the classical criterion: to violate the Plateau stability one must either be close to
![]() $L_{crit}/L=1$
or potentially wait a long time. Notably, while this is a ‘long time’ in MD simulations, from the macroscopic perspective the time scales on which classical stability is lost are miniscule.
$L_{crit}/L=1$
or potentially wait a long time. Notably, while this is a ‘long time’ in MD simulations, from the macroscopic perspective the time scales on which classical stability is lost are miniscule.

Figure 5. Selected realisations for the break-up of classically stable cylinders (i.e. those satisfying the Plateau stability criterion). The two simulations on the left satisfy periodic boundary conditions, those on the right are bounded by a wall (in blue). Non-dimensional time
![]() $t^{\ast }=t/\unicode[STIX]{x1D70F}$
.
$t^{\ast }=t/\unicode[STIX]{x1D70F}$
.

Figure 6. The non-dimensional break-up time (
![]() $t_{b}^{\ast }=t_{b}/\unicode[STIX]{x1D70F}$
) of short nanocylinders near the classical stability boundary, obtained from MD.
$t_{b}^{\ast }=t_{b}/\unicode[STIX]{x1D70F}$
) of short nanocylinders near the classical stability boundary, obtained from MD.
![]() $L_{crit}/L=2\unicode[STIX]{x03C0}r_{0}/L=kr_{0}$
. Error bars indicate one standard deviation of
$L_{crit}/L=2\unicode[STIX]{x03C0}r_{0}/L=kr_{0}$
. Error bars indicate one standard deviation of
![]() $t_{b}^{\ast }$
either side of the mean.
$t_{b}^{\ast }$
either side of the mean.
5 Conclusions
The SLE has been shown to be a remarkably robust tool for extending classical RP arguments into the nanoscale, predicting the loss of a clear-cut Plateau stability boundary and the modification of
![]() $k_{max}$
due to thermal fluctuations, at a fraction of the computational cost of the benchmark MD. More generally, the underlying formulation based on fluctuating hydrodynamics has been confirmed as a useful framework for investigating nanoscale flows; whilst the deterministic nature of classical hydrodynamics is lost, nanoflows can apparently often be well described with (stochastic) partial differential equations without resorting to particle methods.
$k_{max}$
due to thermal fluctuations, at a fraction of the computational cost of the benchmark MD. More generally, the underlying formulation based on fluctuating hydrodynamics has been confirmed as a useful framework for investigating nanoscale flows; whilst the deterministic nature of classical hydrodynamics is lost, nanoflows can apparently often be well described with (stochastic) partial differential equations without resorting to particle methods.
Promisingly, the effects of thermal fluctuations on capillary flows have previously been observed in experiments (Hennequin et al.
Reference Hennequin, Aarts, van der Wiel, Wegdam, Eggers, Lekkerkerker and Bonn2006) using ultra-low surface-tension liquid–liquid systems that massively enhance
![]() $\ell _{fluc}$
to bring thermal fluctuations into the optically observable range. It is our hope that such systems can be used to experimentally verify our new predictions, most notably the violation of Plateau stability. Potential extensions of the framework are numerous. For example, to consider phase change phenomena, which are known to affect the break-up of nanocylinders (Kang & Landman Reference Kang and Landman2007), and to explore related flow configurations, such as liquid jets (Moseler & Landman Reference Moseler and Landman2000) where an intriguing open problem is to understand the interplay between fluctuations within the jet and perturbations imposed at the orifice in an attempt to control break-up.
$\ell _{fluc}$
to bring thermal fluctuations into the optically observable range. It is our hope that such systems can be used to experimentally verify our new predictions, most notably the violation of Plateau stability. Potential extensions of the framework are numerous. For example, to consider phase change phenomena, which are known to affect the break-up of nanocylinders (Kang & Landman Reference Kang and Landman2007), and to explore related flow configurations, such as liquid jets (Moseler & Landman Reference Moseler and Landman2000) where an intriguing open problem is to understand the interplay between fluctuations within the jet and perturbations imposed at the orifice in an attempt to control break-up.
Acknowledgements
Useful discussions with Dr L. Gibelli and Dr J. C. Padrino are gratefully acknowledged. This work was supported by the Leverhulme Trust (Research Project Grant) and the EPSRC (grants EP/N016602/1, EP/P020887/1 & EP/P031684/1).







