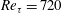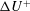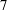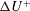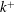1 Introduction
Rough surfaces are found in many forms in engineering systems (Evans Reference Evans1981; Stout, Davis & Sullivan Reference Stout, Davis and Sullivan1990; Bons Reference Bons2010) and in the environment (Finnigan Reference Finnigan2000; Britter & Hanna Reference Britter and Hanna2003). The presence of roughness is known to affect many properties of near-wall turbulent flow (Schlichting & Gersten Reference Schlichting and Gersten2003; Jiménez Reference Jiménez2004). Most importantly, an increase of the skin friction is observed compared to the smooth-wall case. This is connected to a downwards shift in the mean velocity profile, which can be parametrised using the roughness function
$\unicode[STIX]{x0394}U^{+}$
. Rough surfaces are also known to affect the level of turbulent fluctuations, the transition to turbulence and the spatial correlation of characteristic flow structures. It has long been established that aerodynamic effects of roughness are Reynolds-number-dependent (Nikuradse Reference Nikuradse1933). The key governing parameter is
$k^{+}$
, i.e. the characteristic roughness height scale of the surface over the viscous length scale of the flow
$\ell _{\unicode[STIX]{x1D708}}$
.
Based on the sand-grain roughness in the seminal Nikuradse (Reference Nikuradse1933) experiments, three different regimes have been established for rough-wall turbulent flow: aerodynamically smooth, transitionally rough and fully rough. In the fully rough regime, the friction factor becomes independent of the Reynolds number, and for any surface an equivalent sand-grain roughness
$k_{s}^{+}$
can be established by matching the roughness function
$\unicode[STIX]{x0394}U^{+}$
to Nikuradse’s sand-grain roughness data. In the aerodynamically smooth regime, the surface roughness
$k^{+}$
is of the order of the thickness of the viscous sublayer or smaller, and the roughness has no significant influence on the flow. The transitionally rough regime, which occurs for moderate values of
$k^{+}$
is the least well understood; here, different surfaces show the largest amount of variation (Jiménez Reference Jiménez2004), and no universal behaviour is observed.
Traditionally, both experimental and numerical studies on the fundamental properties of turbulent flow over rough surfaces have mainly investigated rather artificial rough surfaces composed of roughness elements such as cubes, bars or cones (Schlichting Reference Schlichting1936; Orlandi & Leonardi Reference Orlandi and Leonardi2009; Akomah, Hangan & Naughton Reference Akomah, Hangan and Naughton2011; Lee, Sung & Krogstad Reference Lee, Sung and Krogstad2011). Advances in experimental measurement techniques and increased computational resources have in more recent years enabled detailed studies of turbulent flow over more irregular forms of rough surfaces that show a much stronger resemblance to most forms of roughness found in engineering applications (Mejia-Alvarez & Christensen Reference Mejia-Alvarez and Christensen2010; Cardillo et al. Reference Cardillo, Chen, Araya, Newman, Jansen and Castillo2013; Yuan & Piomelli Reference Yuan and Piomelli2014; Busse, Luetzner & Sandham Reference Busse, Lützner and Sandham2015). Most of these studies focus on the flow above the rough surface, where for example very-large-scale secondary flow structures have recently been identified (Mejia-Alvarez & Christensen Reference Mejia-Alvarez and Christensen2013; Barros & Christensen Reference Barros and Christensen2014; Anderson et al. Reference Anderson, Barros, Christensen and Awasthi2015).
The direct effect of a rough surface on the velocity field decreases with increasing distance from the rough surface. According to Townsend’s hypothesis (Townsend Reference Townsend1976), the flow in the outer layer, i.e. at a distance from the wall beyond a few roughness heights, is independent of the surface condition, i.e. rough-wall flow will be identical to smooth-wall flow, provided that the ratio
$\unicode[STIX]{x1D6FF}/k$
of boundary layer thickness (or channel half-height)
$\unicode[STIX]{x1D6FF}$
to roughness height
$k$
is small. In support of this hypothesis, Flack, Schultz & Shapiro (Reference Flack, Schultz and Shapiro2005), Wu & Christensen (Reference Wu and Christensen2007) and others found a collapse of mean flow, Reynolds stress and higher-order turbulence statistics in the outer layer for a range of different rough surfaces. Typically, the collapse is postponed to higher distances from the wall for higher-order turbulence statistics (Schultz & Flack Reference Schultz and Flack2005). A collapse of first- and second-order statistics can be achieved for
$\unicode[STIX]{x1D6FF}/k$
ratios as low as
$6.75$
in the context of turbulent pipe flow (Chan et al.
Reference Chan, MacDonald, Chung, Hutchins and Ooi2015).
Closer to the rough surface, the time-averaged velocity field shows significant spatial inhomogeneities induced by the presence of the surface roughness (Bottema Reference Bottema1996; Florens, Eiff & Moulin Reference Florens, Eiff and Moulin2013). This part of the flow is called the roughness sublayer. The roughness sublayer has mainly been investigated in the context of geophysical fluid dynamics, e.g. for flow over block-like urban roughness (see e.g. Cheng & Castro Reference Cheng and Castro2002) or bar and cubic roughness in open channels (see e.g. Pokrajac et al. Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007; Florens et al. Reference Florens, Eiff and Moulin2013). The roughness sublayer typically extends up to a height of two to five times the roughness height into the flow (Raupach, Antonia & Rajagopalan Reference Raupach, Antonia and Rajagopalan1991). The large variation in thickness of the roughness sublayer is due to the influence of both the roughness topography and the flow conditions (Pokrajac et al. Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007).
Comparatively little attention has been paid to the flow in the immediate vicinity of and within the canopy of the rough surface, an area of the flow that has to undergo large changes as the viscous sublayer breaks up in the transitionally rough regime. This is mainly due to measurement difficulties in experiments caused, for example, by reflection and scattering at the rough surface in the case of optical measurement techniques such as particle image velocimetry. In this study the changes in the flow near the surface are investigated using direct numerical simulations (DNS) of rough-wall turbulent channel flow over a range of Reynolds numbers. Two different rough surfaces are studied, which are based on surface scans of realistic specimens of engineering rough surfaces. These irregular surfaces are more representative of real-world rough surfaces than traditional rough surfaces constructed from basic elements such as blocks and cones (see e.g. Schlichting Reference Schlichting1936; Krogstad et al. Reference Krogstad, Andersson, Bakken and Ashrafian2005; Orlandi & Leonardi Reference Orlandi and Leonardi2008). Using DNS we are able to measure the flow not only above the rough surfaces but also within the rough surfaces, i.e. in a region where experimental measurements are very difficult to obtain.
With increasing Reynolds number of the flow, the roughness height grows compared to the viscous length scale of the turbulence, and the flow goes from transitionally rough towards a fully rough state. With increasing roughness height
$k^{+}$
, the original viscous sublayer is destroyed. In this work the time-averaged flow field near the wall is studied in detail; it emerges that the destruction of the viscous sublayer is incomplete, and for rough surfaces with suitable characteristics viscous sublayer patches can be observed at higher Reynolds number in areas where the flow can closely adapt to the rough surface. The article is structured as follows. First, § 2 discusses the surfaces studied and the methodology employed for the DNS. In § 3 results for the mean flow quantities are presented. The properties of the near-wall flow field are characterised in § 4. A physical interpretation of these results is discussed in more detail in § 5. A summary and final conclusions are given in § 6.
2 Methodology
In the first subsection we discuss the properties of the two rough surfaces that have been used in the simulations. In the second subsection the numerical method used for the DNS of turbulent channel flow over these surfaces is described.
2.1 The surfaces
The first surface is taken from a sample of graphite (supplied by Gas Dynamics Ltd, UK) and the second surface from a standard roughness comparator for a grit-blasted surface (supplied by Rubert & Co. Ltd, UK). In both cases, the surfaces were scanned; the data obtained from the scans were then post-processed by applying a low-pass Fourier filter. A brief description of the filtering procedure is given in appendix A. This resulted in smoothly varying surfaces that are compatible with the application of periodic boundary conditions. Full details of the filtering procedure are described in Busse et al. (Reference Busse, Lützner and Sandham2015).
Figure 1. Topographies of the rough surfaces: (a) graphite surface and (b) grit-blasted surface.
Table 1. Topographical surface parameters for the two surfaces studied. All length scales are given in multiples of the mean channel half-height
$\unicode[STIX]{x1D6FF}$
. The definitions of the parameters can be found in Mainsah, Greenwood & Chetwynd (Reference Mainsah, Greenwood and Chetwynd2001) and Busse et al. (Reference Busse, Lützner and Sandham2015)
The filtered surfaces have been characterised using a number of topographical parameters, which are given in table 1. Both surfaces were scaled to the same mean peak-to-valley height
$S_{z,5\times 5}$
, which characterises the average height difference between the highest peaks and the deepest valleys of the surface. The surfaces are illustrated in figure 1. As can be observed, other height parameters such as the mean roughness height
$S_{a}$
and root-mean-square (r.m.s.) roughness height
$S_{q}$
are also quite similar for the two surfaces. The correlation lengths in the streamwise and spanwise directions
$L_{x}^{cor}$
and
$L_{y}^{cor}$
are of comparable magnitude for the two surfaces. The effective slope
$ES_{x}$
of the surfaces is moderate and in both cases below the critical slope
$ES_{x}^{\text{crit}}=0.35$
proposed by Schultz & Flack (Reference Schultz and Flack2009). Moderate effective slopes are typical of many rough surfaces generated by erosion processes.
Figure 2. Height distribution of the graphite and the grit-blasted surface.
Since in both cases the surface texture aspect ratio
$S_{tr}$
is greater than
$0.5$
, both surfaces can be considered as statistically isotropic, i.e. they do not possess a preferential direction. The effective slopes observed for the graphite surface are approximately
$25\,\%$
higher than for the grit-blasted surface. The biggest distinction between the two surfaces is their skewness factor
$S_{sk}$
, i.e. the skewness of the height distribution of the surfaces (see figure 2). The graphite surface has a positively skewed height distribution, which means that on average the peaks are more pronounced whereas the valleys of the surface are comparatively shallow. The grit-blasted surface is negatively skewed, indicating the presence of deep valleys and relatively flat peaks.
Apart from the roughness Reynolds number, another important parameter to classify turbulent flow over rough surfaces is the ratio between the characteristic macroscopic length scale of the flow
$\unicode[STIX]{x1D6FF}$
, i.e. the channel half-height or the boundary layer thickness, and the roughness height
$k$
. There are many different approaches as to how to define the roughness height
$k$
topographically. For example, in table 1 three different height measures are given with
$S_{a}$
,
$S_{q}$
and
$S_{z,5\times 5}$
and more height measures exist (Mainsah et al.
Reference Mainsah, Greenwood and Chetwynd2001). All three height measures have been used to quantify
$k$
in the context of rough-wall turbulent flows (Schultz & Flack Reference Schultz and Flack2009; Bons Reference Bons2010; Thakkar, Busse & Sandham Reference Thakkar, Busse and Sandham2015). Dependent on whether
$k$
is based on
$S_{a}$
,
$S_{q}$
or
$S_{z,5\times 5}$
, the ratio
$\unicode[STIX]{x1D6FF}/k$
varies between
${\approx}37$
and
$6$
. Jiménez (Reference Jiménez2004) states that universal behaviour in the outer layer should be observed for cases where
$\unicode[STIX]{x1D6FF}/k>40$
. We will see later that
$S_{z,5\times 5}$
is close to the equivalent sand-grain roughness of the surfaces and thus appears to be a suitable measure for
$k$
. The resulting
$\unicode[STIX]{x1D6FF}/k=6$
indicates that we are in a regime where a certain degree of non-universal behaviour can be expected, but this regime is of high practical relevance, since in many examples of turbulent flow over rough surfaces
$\unicode[STIX]{x1D6FF}/k$
is significantly lower than
$40$
(Sadeh, Cermak & Kawatani Reference Sadeh, Cermak and Kawatani1971; Bogard, Schmidt & Tabbita Reference Bogard, Schmidt and Tabbita1998; Wood et al.
Reference Wood, Banaj, Turnock, Wang and Evans2010).
DNS of turbulent flow over irregular rough surfaces has more stringent resolution requirements than simulations for standard smooth-wall turbulent flows (Busse et al.
Reference Busse, Lützner and Sandham2015). Computational resources thus limit both the scale of the roughness, since very small roughness features would be difficult to resolve, and the attainable Reynolds numbers. Most previous DNS of turbulent flow over rough surfaces have also been conducted at
$\unicode[STIX]{x1D6FF}/k\ll 40$
(Leonardi et al.
Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003; Napoli, Armenio & De Marchis Reference Napoli, Armenio and De Marchis2008; Orlandi & Leonardi Reference Orlandi and Leonardi2008; Chau & Bhaganagar Reference Chau and Bhaganagar2012; Chan et al.
Reference Chan, MacDonald, Chung, Hutchins and Ooi2015). As is shown in the following, close to universal behaviour of the mean flow in the outer layer can still be observed at this
$\unicode[STIX]{x1D6FF}/k$
ratio.
2.2 Direct numerical simulations
In the DNS the rough surfaces are applied as boundary conditions to both the upper and the lower wall of the channel. The surface on the upper wall of the channel is shifted by half the domain size in the streamwise and spanwise directions in order to minimise local blockage effects. In the streamwise and spanwise directions periodic boundary conditions are employed. Chan et al. (Reference Chan, MacDonald, Chung, Hutchins and Ooi2015) found in the context of turbulent pipe flow that the virtual origin of a rough pipe corresponds to its mean hydraulic radius. In the current channel flow simulations, the mean height of the rough surfaces has been set to zero, giving a mean channel half-height of
$\unicode[STIX]{x1D6FF}$
. The coordinate
$z=0$
will be used in the following as the virtual origin of the wall, which is consistent with the findings of Chan et al. (Reference Chan, MacDonald, Chung, Hutchins and Ooi2015).
The turbulent flow over the surface was simulated using the embedded boundary code iIMB. Second-order central differences are used to discretise the spatial derivatives of the incompressible Navier–Stokes equations and a second-order Adams–Bashforth scheme for the discretisation in time. An iterative version of the embedded boundary method of Yang & Balaras (Reference Yang and Balaras2006) is used to resolve the rough walls. A brief description of the embedded boundary method is given in appendix B. Full details can be found in Busse et al. (Reference Busse, Lützner and Sandham2015), including grid and filter sensitivity studies.
The flow is driven by a mean streamwise pressure gradient
$\unicode[STIX]{x1D6F1}$
, which is uniform in space and constant in time. Using
$\unicode[STIX]{x1D6F1}$
, the mean channel half-height
$\unicode[STIX]{x1D6FF}$
and the constant density
$\unicode[STIX]{x1D70C}$
, the friction velocity can be determined (Pope Reference Pope2000):
$$\begin{eqnarray}u_{\unicode[STIX]{x1D70F}}=\left(-\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6F1}\right)^{1/2}.\end{eqnarray}$$
In the following, all velocity values are given in multiples of the friction velocity
$u_{\unicode[STIX]{x1D70F}}$
.
Table 2. Domain and grid sizes of the rough-wall simulations.
Key parameters for the simulations are summarised in table 2. In all cases the mesh is uniformly spaced in the streamwise (
$x$
) and spanwise (
$y$
) directions and stretched in the wall-normal (
$z$
) direction. Within the roughness layer, i.e. between the minimum and maximum elevations of the rough surfaces, a uniform spacing
$\unicode[STIX]{x0394}z_{min}$
is used in the wall-normal direction. Above the rough surface the mesh spacing
$\unicode[STIX]{x0394}z$
is gradually increased, attaining the maximum spacing of
$\unicode[STIX]{x0394}z_{max}$
in the channel centre. The mesh spacing in the streamwise and spanwise directions is influenced by two factors: the need to capture the complex structure of the rough surfaces and the need to resolve the finest turbulent structures in the flow. For the simulations considered here, the first factor is the deciding one at low
$Re_{\unicode[STIX]{x1D70F}}$
while the second factor is dominant at higher
$Re_{\unicode[STIX]{x1D70F}}$
.
The domain sizes for both surfaces are determined by the size of the surface scan and the applied scaling. It has been tested that the domain sizes are sufficiently large by comparing the mean flow and Reynolds stresses for a simulation with a single tile of the rough surface pattern (as used in the current simulations) to a simulation with double the domain size in the streamwise and spanwise directions using
$2\times 2$
tiles of the rough surface pattern. A close agreement was found (Busse et al.
Reference Busse, Lützner and Sandham2015).
3 Mean velocity statistics
The roughness function parametrises the aerodynamic roughness effects of the surfaces. The underlying mean streamwise velocity profiles undergo significant changes in the vicinity of the rough walls as Reynolds number is increased.
3.1 Roughness function
For all
$Re_{\unicode[STIX]{x1D70F}}$
the rough surfaces have a clear effect on the flow. For the higher Reynolds-number cases (
$Re_{\unicode[STIX]{x1D70F}}=360,~540,~720$
) the bulk flow velocity
$U_{b}$
attains an approximately constant value with differences below
$2.5\,\%$
. The effective friction factor for these cases is thus approximately independent of the Reynolds number, as we would expect for the fully rough regime.
Values of
$\unicode[STIX]{x0394}U^{+}$
were measured by subtracting the value of the centreline velocity
$U_{c}$
from the centreline velocity in the reference (smooth-wall) case
$U_{c}^{ref}$
. This measure was chosen to have a consistent way of measuring
$\unicode[STIX]{x0394}U^{+}$
that works well for all
$Re_{\unicode[STIX]{x1D70F}}$
, since at low
$Re_{\unicode[STIX]{x1D70F}}$
the velocity profile does not show a clear log law (Moser, Kim & Mansour Reference Moser, Kim and Mansour1999; Busse & Sandham Reference Busse and Sandham2012; Chung et al.
Reference Chung, Chan, MacDonald, Hutchins and Ooi2015). The measured values of roughness function
$\unicode[STIX]{x0394}U^{+}$
(see table 3 and figure 3 for both surfaces) also indicate that the flow would normally be classified as being in the fully rough regime for the higher Reynolds numbers, since for these cases
$\unicode[STIX]{x0394}U^{+}$
is close to
$7$
or above, corresponding to
$k_{s}^{+}>70$
.
Figure 3. (a) Roughness function versus mean peak-to-valley height. (b) Roughness function versus estimated equivalent sand-grain roughness; the fully rough asymptote and the Colebrook formula are shown for comparison.
Table 3. Centreline velocity, bulk flow velocity and roughness functions for the graphite and grit-blasted surfaces at different Reynolds numbers.
The
$\unicode[STIX]{x0394}U^{+}$
values for both surfaces are of similar magnitude, which can be attributed to the fact that many surface parameters, such as roughness height, texture aspect ratio, effective slopes and correlation lengths, are similar for both surfaces. The graphite surface gives higher values for
$\unicode[STIX]{x0394}U^{+}$
at all
$Re_{\unicode[STIX]{x1D70F}}$
, which we attribute to the higher skewness factor of this surface, i.e. the peaks of a surface are more relevant for the aerodynamic properties than the valleys (Flack & Schultz Reference Flack and Schultz2010). At the lower
$S_{z,5\times 5}^{+}$
values, we still observe significant values for
$\unicode[STIX]{x0394}U^{+}$
. Similar observations were made for the sinusoidally patterned pipe surfaces studied in the DNS by Chan et al. (Reference Chan, MacDonald, Chung, Hutchins and Ooi2015), which also showed a relatively steep increase of the roughness function with
$k_{s}^{+}$
in the upper transitionally rough region, as observed for the current simulations.
By matching the
$\unicode[STIX]{x0394}U^{+}$
values at higher
$Re_{\unicode[STIX]{x1D70F}}$
to the expected fully rough behaviour (see figure 3
b), the equivalent sand-grain roughness of the surfaces can be established. For the grit-blasted surface, the equivalent sand-grain roughness is approximately equal to the mean peak-to-valley height
$k_{s,eqv}\approx S_{z,5\times 5}$
, while for the graphite surface
$k_{s,eqv}\approx (4/3)S_{z,5\times 5}$
. This shows that for these surfaces
$S_{z,5\times 5}$
gives a good first approximation for
$k_{s,eqv}$
. The approximation is much better than basing an approximation
$k_{s,eqv}$
on other roughness height scales, such as the mean roughness height
$S_{a}$
or the r.m.s. roughness height
$S_{q}$
, which are the main roughness height indicators that have been used in previous work on turbulent flow over irregular rough surfaces (Bons Reference Bons2010; Flack & Schultz Reference Flack and Schultz2010):
$S_{q}$
and
$S_{a}$
give measures for the average height and depths of the peaks and valleys of a surface, whereas
$S_{z,5\times 5}$
is determined by the highest peaks and deepest valleys. The highest peaks of a rough surface have a dominant effect on its aerodynamic characteristics and thus their magnitude should be reflected in the aerodynamic roughness height measure.
3.2 Mean velocity profile
The mean velocity profiles, plotted in semi-logarithmic form in figure 4, show an increasing downwards shift for
$z^{+}>10$
with increasing Reynolds number, i.e. roughness effects increase with
$Re_{\unicode[STIX]{x1D70F}}$
, as expected. For
$z^{+}\approx 1$
the profiles show the opposite trend, with increasing mean velocity as
$Re_{\unicode[STIX]{x1D70F}}$
is increased, indicating increased flow rates towards the centre of the roughness layer, which is located at
$z=0$
. For higher
$Re_{\unicode[STIX]{x1D70F}}$
, the velocity defect profile shown on figure 5 shows a good collapse for almost all
$z/\unicode[STIX]{x1D6FF}$
values, indicating that the profile in the outer region of the flow has already attained an approximately Reynolds-number-independent shape, in spite of the relatively low value of
$\unicode[STIX]{x1D6FF}/k$
. Larger differences occur only in the immediate vicinity of the rough wall.
Figure 4. Semi-logarithmic profiles of mean streamwise velocity at different Reynolds numbers: (a) graphite surface and (b) grit-blasted surface.
Figure 5. Mean velocity defect profiles: (a) graphite case and (b) grit-blasted case.
Figure 6. Diagnostic quantity for a log law: (a) graphite case and (b) grit-blasted case.
Figure 7. Diagnostic quantity for a power-law: (a) graphite case and (b) grit-blasted case.
It has already been noted that velocity profiles at low
$Re_{\unicode[STIX]{x1D70F}}$
do not show a clear semi-logarithmic behaviour and at higher
$Re_{\unicode[STIX]{x1D70F}}$
there has been debate about whether the log law applies, or whether the mean flow profile is better described by a power law (Gad-el-Hak & Buschmann Reference Gad-el-Hak and Buschmann2011). From DNS data for turbulent smooth-wall channel flow, we know that at least up to Reynolds number
$Re_{\unicode[STIX]{x1D70F}}=2000$
no clear log law can be observed, since the diagnostic quantity
$\unicode[STIX]{x1D6FE}=z^{+}\,\text{d}U^{+}/\text{d}z^{+}$
does not show a constant range, as would be consistent with a true log law (George Reference George2007). However, an alternative scaling of the velocity profile in the form of a power law, which should give a constant value for the diagnostic quantity
$\unicode[STIX]{x1D6FD}=(z^{+}/U^{+})\,\text{d}U^{+}/\text{d}z^{+}$
, has also not been very successful (Moser et al.
Reference Moser, Kim and Mansour1999). In the current (rough-wall) mean streamwise velocity profiles, we see an approximately logarithmic region in the mean streamwise velocity profiles at the higher Reynolds numbers (see figure 4). A closer evaluation of the profiles using the diagnostic quantities
$\unicode[STIX]{x1D6FE}$
(for log-law behaviour) and
$\unicode[STIX]{x1D6FD}$
(for power-law behaviour) shows that the situation is more complex. The graphite surface gives rise to a comparatively well-developed log law (see figure 6) where
$\unicode[STIX]{x1D6FE}$
is far closer to a constant behaviour than is observed for smooth-wall cases at comparable Reynolds numbers. For the grit-blasted surface, on the other hand, almost perfect power-law scaling can be observed (see figure 7). In both cases the
$z^{+}$
ranges over which approximate logarithmic or power-law scaling is observed are above the highest features of the surface. The spikes that can be observed in the
$\unicode[STIX]{x1D6FE}$
values at lower
$z^{+}$
correspond to the heights of the highest roughness features. We have currently no explanation why this is the case, and indeed the observed scaling may break down at higher
$Re_{\unicode[STIX]{x1D70F}}$
, but we can only state that the existence of a universal near-wall behaviour is even less likely for rough-wall flows than for the smooth-wall case. Investigation of a wider range of surfaces will be required to establish whether the observed different scaling laws are coincidental or tied to topographical features of a rough surface.
Figure 8. Mean velocity profiles with linear
$x$
-axis: (a) graphite case and (b) grit-blasted case. The insets show the derivative of the mean velocity profile near the mean wall plane.
Figure 9. Mean velocity profiles in the near-wall region: (a) graphite case and (b) grit-blasted case.
Mean velocity profiles in linear coordinates are shown in figure 8. While the flow near the channel centreline shows the same reduction in velocity that was seen on the semi-logarithmic plot (figure 4), in the upper part of the rough surface (roughly for
$0<z<0.1$
) the mean streamwise velocity increases approximately linearly in the case of the higher Reynolds-number cases. The slope is shown in the inset, illustrating that
$\text{d}U^{+}/\text{d}z^{+}$
has an approximately constant value up to
$z^{+}\approx 40$
for the
$Re_{\unicode[STIX]{x1D70F}}=720$
cases. At the upper end of the linear range the mean streamwise velocity has attained a value of
$U^{+}\geqslant 5$
. This shows some resemblance to the linear scaling in the viscous sublayer of a smooth-wall turbulent flow, but the analogy is imperfect, since the slope of the linear increase is significantly lower than one and decreases with increasing Reynolds number.
The near-wall region is shown in expanded form in figure 9. Within the rough surface, the velocity profile
$U(z)$
is obtained by plane averaging the time-averaged streamwise velocity component over the area occupied by the fluid. For most of the lower part of the rough surface the time-averaged flow is reversed, i.e.
$\overline{u}(x,y)<0$
. Negative mean streamwise velocity within the roughness canopy is also found for other types of roughness. For example, for transverse bar roughness, strong reverse flows are an inevitable consequence of the roughness topography unless the bars are very widely spaced (Leonardi et al.
Reference Leonardi, Orlandi, Djenidi and Antonia2004). A higher magnitude of reversed flow is observed for the grit-blasted case, which is probably attributable to its negative surface skewness (negative skewness means deeper cavities, which allow development of stronger reverse flows). The deepest cavity for the grit-blasted surface extends to
$z/\unicode[STIX]{x1D6FF}=-0.159$
, whereas the deepest cavity in the graphite surface extends to
$z/\unicode[STIX]{x1D6FF}=-0.115$
. The strength of reversed flow increases with increasing Reynolds number for both surfaces. The highest
$z/\unicode[STIX]{x1D6FF}$
value for which the mean streamwise velocity profile is negative increases when going from
$Re_{\unicode[STIX]{x1D70F}}=90$
to
$Re_{\unicode[STIX]{x1D70F}}=180$
, but decreases again as the Reynolds number increases further. This region will be examined in more detail in § 4.2 below.
3.3 Viscous and form drag
The values of the mean frictional drag
$T_{x}$
and form drag
$F_{x}$
have been obtained by computing the volume average of the streamwise component of viscous term and the fluctuating pressure gradient term. Since an embedded boundary method is used, the influence of the embedded boundary force term has been included by adding the surface-tangential component of the streamwise embedded boundary force vector to the viscous part and the surface-normal component to the form drag. The mean frictional drag
$T_{x}$
and form drag
$F_{x}$
at different Reynolds numbers are shown in figure 10. The frictional part of the drag decreases with
$Re_{\unicode[STIX]{x1D70F}}$
whereas the form drag increases. In the fully rough regime the frictional drag should be dominated by the form drag (Schultz & Flack Reference Schultz and Flack2009). In the current cases, the form drag clearly exceeds the frictional drag for
$Re_{\unicode[STIX]{x1D70F}}>360$
. However, at higher Reynolds numbers, an appreciable frictional drag component remains. The ratio of frictional to form drag decreases with increasing
$Re_{\unicode[STIX]{x1D70F}}$
but never drops below 30 % of the total drag, even though the values of
$\unicode[STIX]{x0394}U^{+}$
are high enough for the flow to be classified as fully rough and the mean velocity profile has attained a nearly Reynolds-number-independent shape in the outer layer of the flow (see figure 5). The surfaces studied have effective slopes
$ES_{x}$
below the threshold of
$0.35$
identified by Napoli et al. (Reference Napoli, Armenio and De Marchis2008), which may account for relatively high frictional drag. Moderate effective slope values are fairly common for engineering rough surfaces; for example, most of the realistic surfaces studied by Yuan & Piomelli (Reference Yuan and Piomelli2014) also had effective slopes below
$0.35$
. Additionally, owing to the low-pass-filtered nature of the surfaces studied here, the surfaces are smooth for scales below the wavelength of the smallest retained Fourier wavelength. As the Reynolds number increases, the viscous scale reduces and the flow can at least partially adapt to the undulating nature of these surfaces, which would not be possible surfaces with singularities in their first derivatives, such as steps, or very high slopes.
Figure 10. Frictional and form drag for the rough surfaces: (a) graphite and (b) grit-blasted surface.
Figure 11. Variation of friction factor with Reynolds number, where
$\unicode[STIX]{x1D706}$
is the friction factor (dimensionless pressure drop per unit length of channel/pipe) and
$Re$
is the bulk Reynolds number. For comparison are Nikuradse’s data for different sand-grain roughness heights relative to the pipe radius
$R$
and data from DNS of smooth-wall turbulent channel flow (including data from Lee & Moser (Reference Lee and Moser2015)). Also shown are the analytic relationships for the smooth-wall laminar pipe and channel flow cases. The Blasius and Dean’s relationships are shown for the fully developed smooth-wall turbulent pipe and channel flow cases.
The dependence of the effective friction factor
$\unicode[STIX]{x1D706}$
on the Reynolds number is shown in figure 11 in the context of Nikuradse’s (Reference Nikuradse1933) data for rough pipes. Pipe flow data are shown in grey whereas black lines and symbols refer to channel flow data. For both surfaces, the friction factor shows a big increase over the smooth-wall values. The friction factor increases with Reynolds number, and attains an approximately constant level at the highest Reynolds numbers, so the fully rough regime appears to be attained. The data follow the trends shown by Nikuradse’s experiments – with decreasing ratio of channel half-height (or pipe radius) to roughness height, the fully rough regime is reached at lower Reynolds numbers. In the transitionally rough regime, an increase in the friction factor is observed, so the current data (like Nikuradse’s data) disagree with the trend predicted by the Moody chart, which shows a decrease of the friction factor with Reynolds number in the transitionally rough region.
Based on the observations described above, the transition between the transitionally rough and the fully rough regimes (with supposedly universal behaviour) is not as clear-cut as it may seem. Based on a number of criteria, such as the value of
$\unicode[STIX]{x0394}U^{+}$
, the Reynolds-number dependence of the friction factor and the bulk flow profile, and the dominance of the form drag over the friction drag, the two highest Reynolds-number cases for both surfaces can be classified as fully rough. However, when taking a closer look at quantities directly influenced by the detailed near-wall flow, such as the remaining frictional drag component or the reversed mean flow near the wall, these cases still show significant Reynolds-number dependence. A truly universal, roughness-only determined state is thus not attained at these Reynolds numbers, even though the bulk flow appears to be insensitive to whether the surface drag at small wavelengths is provided by small roughness elements or by viscous stresses over locally smooth surfaces.
4 The flow in the near-wall layer
In the context of the mean velocity profile, some striking features of the flow near the wall have already been discussed, including a layer of reverse flow deep in the rough surface and a linear region in the outer part of the rough surface. In this section, the flow near the surface will be discussed in more detail. We start our characterisation of the near-wall flow by estimating the thickness of the roughness sublayer based on the spatial inhomogeneity of the time-averaged velocity field. We then proceed to characterise the flow very close to the wall within the roughness canopy by considering probability density functions (p.d.f.s) of reverse flow, before investigating the breakdown of the viscous sublayer and the emergence of what is termed a ‘blanket’ layer as the flow at high Reynolds number increasingly conforms to the largest surface features.
4.1 Roughness sublayer
The roughness sublayer is the region of flow near the wall where the flow is very strongly influenced by the presence of roughness elements or surface features, leading to spatial inhomogeneities in the flow field (Cheng et al.
Reference Cheng, Hayden, Robins and Castro2007). The thickness of the roughness sublayer can be measured based on the dispersive stresses of the flow field (Pokrajac et al.
Reference Pokrajac, Campbell, Nikora, Manes and McEwan2007; Florens et al.
Reference Florens, Eiff and Moulin2013),
$u_{i}^{\prime \prime }=\overline{u_{i}}-\langle \overline{u_{i}}\rangle _{xy}$
, i.e. the difference between the local time-averaged value of a velocity component and its time- and plane-averaged value. In figure 12 the standard deviation of the time-averaged wall-normal velocity, normalised by the mean streamwise velocity at the same wall-normal location, is shown. As expected, high values of the dispersive stresses are found within the lower part of the roughness sublayer. In the upper part of the roughness sublayer a rapid decrease can be observed. Further away from the wall, the decrease continues albeit at a much slower rate. The vertical fluctuations
$\sqrt{\langle w^{\prime \prime 2}\rangle }/U$
show a weak increase with Reynolds number. The levels of this quantity tend to be slightly higher for the graphite surface, which may be a consequence of the positive skewness of this surface.
Figure 12. Standard deviation of time-averaged wall-normal velocity normalised by streamwise mean velocity (percentage values): (a) graphite surface and (b) grit-blasted surface. The horizontal red line shows the
$5\,\%$
level.
The value of
$\sqrt{\langle w^{\prime \prime 2}\rangle }/U$
drops below 5 % just above the highest roughness features for the highest Reynolds numbers, which can be taken as an estimate for the thickness of the roughness sublayer. Based on a threshold value of
$2.5\,\%$
the roughness layer extends up to
$z\approx 0.25\unicode[STIX]{x1D6FF}$
, which would correspond to
${\approx}1$
roughness height above the highest roughness features. For lower Reynolds numbers, the roughness sublayer has a lower thickness. This estimated thickness of the roughness sublayer for the current surfaces is of comparable magnitude to measurements of the roughness sublayer thickness in experiments of turbulent flows over dense cubic roughness (Cheng & Castro Reference Cheng and Castro2002; Florens et al.
Reference Florens, Eiff and Moulin2013), where an extent of the roughness sublayer of
${\approx}0.75{-}1.2$
roughness heights above the roughness canopy was found.
4.2 Reverse flow
In the case of two-dimensional wavy surfaces, or surfaces with transverse bars, a reverse flow region forms on the leeward-facing side of the waves or bars (Maass & Schumann Reference Maass and Schumann1994; Cherukat et al. Reference Cherukat, Na, Hanratty and McLaughlin1998; Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003; Napoli et al. Reference Napoli, Armenio and De Marchis2008). For the current surfaces, the situation is more complex, since the surfaces also show variations in the transverse direction, which allows the near-wall flow to circumnavigate some of the roughness features. Nevertheless, significant flow reversal exists, even in the mean flow, as was shown in figure 9. Since the current surfaces are differentiable, i.e. they show no sharp corners or edges, the separation points and lines are not fixed. We can thus expect that the degree of flow reversal depends on the Reynolds number of the flow.
Figure 13. Probability of negative
$\overline{u}$
versus wall-normal coordinate
$z$
for different Reynolds numbers: (a) graphite case and (b) grit-blasted case.
Since the reversed flow is tied to the local surface topography, for a given
$z$
value, in some areas of the rough surface the flow may be reversed, while for other areas it remains attached. Here, we take negative time-averaged streamwise velocity as an indicator for the amount of reverse flow. The probability of reversed flow as a function of the distance from the wall is shown in figure 13. As expected, no reversed flow is found for
$z/\unicode[STIX]{x1D6FF}>0.1$
, i.e. in the uppermost parts of the rough surface and above the rough surface. The highest peaks of the surfaces extend up to
$z/\unicode[STIX]{x1D6FF}=0.114$
for the graphite surface and up to
$z/\unicode[STIX]{x1D6FF}=0.103$
for the grit-blasted surface. The reversed flow diagnostic thus suggests that around the highest peaks the mean flow remains attached. In the lower parts of the rough surface, a significant amount of reversed flow is present, which decreases with increasing
$z/\unicode[STIX]{x1D6FF}$
. In the deepest cavities of the surface, the flow is always reversed.
The amount and height distribution of the reversed flow is clearly Reynolds-number-dependent. For low Reynolds numbers (
$Re_{\unicode[STIX]{x1D70F}}=90$
to
$Re_{\unicode[STIX]{x1D70F}}=180$
) the amount of reverse flow increases with increasing Reynolds number. A significant increase can be observed for all surface elevations up to
$z/\unicode[STIX]{x1D6FF}=0.05$
when going from
$Re_{\unicode[STIX]{x1D70F}}=90$
to
$Re_{\unicode[STIX]{x1D70F}}=180$
. At these low Reynolds numbers an increase in the near-wall velocity means that the flow is less able to adapt to the contours of the surface, which increases the probability of flow reversal. For higher Reynolds numbers (
$Re_{\unicode[STIX]{x1D70F}}=240$
,
$360$
,
$540$
and
$720$
) this trend is reversed and the probability of flow reversal decreases. The decrease occurs mostly at
$z/\unicode[STIX]{x1D6FF}$
values below the mean roughness plane, while the probability of reversed flow attains Reynolds-number independence for
$z>0$
. With increasing Reynolds number, the streamwise momentum of the near-wall flow increases further and ‘bubbles’ of reversed flow are ‘eroded’ (i.e. reduced in size), while the mean reverse flow velocity remains high, indicating high velocities within the reverse flow regions that remain.
4.3 Breakdown of viscous sublayer and emergence of a ‘blanketing’ layer
In the viscous sublayer of a smooth wall, the mean velocity profile shows a linear dependence on the distance from the wall; this layer extends approximately up to
$z^{+}=5$
, where the mean flow reaches the value
$U^{+}\approx 5$
. For flow over a rough surface with increasing roughness height, the roughness elements are initially buried within the viscous sublayer, which gradually breaks down in the transitionally rough regime. This breakdown is assumed to be complete once the flow has entered the fully rough regime. However, it is not clear how this breakdown manifests itself and what form the near-wall flow takes once the viscous sublayer is destroyed.
For better quantification of the changes that the near-wall flow undergoes in the transitionally rough regime, we have defined two new statistical quantities. The first quantity is the distance from the mean wall plane (i.e. from
$z=0$
) where the time-averaged streamwise velocity reaches the value
$\overline{u}^{+}=5$
, which locates the upper end of the linear profile at the highest Reynolds number shown in figure 8. This quantity will be called
$z_{\overline{u}^{+}=5}(x,y)$
in the following. The choice
$\overline{u}^{+}=5$
as threshold value is to some degree arbitrary, since
$\overline{u}^{+}=5$
has no special significance in the context of rough-wall flow. However, it makes a reasonable choice since the mean velocity profile shows a linear scaling close to the wall for the higher-Reynolds-number cases (see § 3.2 and figure 8) and attains values of
$U^{+}\geqslant 5$
at the upper end of this linear region. The second quantity considered is the local distance from the rough surface where the time average of the modulus of the velocity vector
$v_{abs}=|\boldsymbol{v}|$
reaches the value
$\overline{v}_{abs}^{+}=5$
named
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}$
, which can be seen as the thickness of this layer. In the case of a smooth-wall flow,
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}=z_{\overline{u}^{+}=5}(x,y)$
, and in wall units both quantities would have a value of
$5$
.
Figure 14. Location of the upper end of the blanketing layer: (a) graphite surface and (b) grit-blasted surface. The red curves show the p.d.f.s for the surface height distributions.
The probability density for
$z_{\overline{u}^{+}=5}$
(in outer units) is shown in figure 14. We observe that, at
$Re_{\unicode[STIX]{x1D70F}}=90$
,
$z_{\overline{u}^{+}=5}$
has a peak at
$z/\unicode[STIX]{x1D6FF}\approx 0.1$
for both surfaces, which corresponds approximately to the location of the highest roughness features. As the Reynolds number increases, the peak moves closer to the wall. This would of course also be expected for a smooth wall, where the p.d.f. peaks at
$z=5\ell _{\unicode[STIX]{x1D708}}$
. However, for
$Re_{\unicode[STIX]{x1D70F}}=240$
and above, the location of the peak does not change significantly.
In the smooth-wall case, the p.d.f. for
$z_{\overline{u}^{+}=5}$
would be a delta-function, i.e. it would have zero width, while for a rough surface, the p.d.f. has a finite width. As the Reynolds number increases, the width of the p.d.f. of
$z_{\overline{u}^{+}=5}$
increases and the height of the peak decreases. For the highest Reynolds numbers studied here, a universal shape of the p.d.f. starts to appear at the higher values of
$z_{\overline{u}^{+}=5}$
, while the probability of small
$z_{\overline{u}^{+}=5}$
values continues to increase with
$Re_{\unicode[STIX]{x1D70F}}$
. At higher Reynolds numbers, the shape of the p.d.f. comes to resemble a shifted version of the p.d.f. of the surface height distribution, indicated by the red lines in the graphs, leading to the terminology of a ‘blanket’ layer. The shifted fit is imperfect, since the p.d.f. for
$z_{\overline{u}^{+}=5}$
is in all cases narrower than the p.d.f. of the surface height distribution, and while the difference between the highest
$z_{\overline{u}^{+}=5}$
values and the highest surface height values is quite small, the lowest
$z_{\overline{u}^{+}=5}$
values that are observed are significantly higher than the lowest surface height values. A further observation is that for the grit-blasted surface there is a stronger mismatch between the surface height p.d.f. and the p.d.f. of
$z_{\overline{u}^{+}=5}$
. This is because of the persistent reversal of the flow in the deep cavities of this valley-dominated surface, which prevents a close match between the blanketing layer and the surface contours.
Figure 15. The p.d.f.s of thickness of blanketing layer: (a) and (c) graphite surface; and (b) and (d) grit-blasted surface. Panels (a) and (b) show the thickness in outer units; and panels (c) and (d) show the thickness in inner units.
How closely the blanketing layer can adapt to the contours of the surface can be further investigated by looking at
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}$
, i.e. the distance from the rough wall at which
$\overline{v}_{abs}^{+}=5$
is attained. The p.d.f.s for this quantity are shown in figure 15 in both inner and outer units. Looking at this quantity in outer units (i.e. scaled by the mean channel half-height
$\unicode[STIX]{x1D6FF}$
), we see quite a wide distribution at all Reynolds numbers. The main change with Reynolds number is that the distribution becomes increasingly positively skewed. This means that part of the blanketing layer can actually follow the surface contours, as evidenced in the peak, which moves to lower
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}/\unicode[STIX]{x1D6FF}$
values and becomes more pronounced as the Reynolds number increases. For large parts of the surfaces, the blanketing layer becomes independent of the wall – evidenced by the long persistent tail to high
$\unicode[STIX]{x0394}z_{\overline{u}^{+}=5}/\unicode[STIX]{x1D6FF}$
values. In inner units, i.e. scaled by the relevant viscous length scale, the change in the p.d.f. manifests itself in an increasingly wide distribution, with a tail to high
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}^{+}$
values, which grows as the Reynolds number increases.
The p.d.f.s show an emerging mixed scaling at higher Reynolds number. The right tail of the p.d.f. starts to collapse and becomes independent of Reynolds number when
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}$
is measured in outer units. This collapse clearly does not occur for the p.d.f. of
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}^{+}$
. On the other hand, the peak that emerges at low
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}$
values continues to grow (and move to lower values) when
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}$
is measured in outer units. The peak approaches a uniform shape and location for the p.d.f. of
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}^{+}$
at the higher Reynolds numbers. The persistence of the inner peak in the p.d.f. of
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}^{+}$
and the increasing conformity of the flow to the surface shown by the p.d.f. of
$z_{\overline{u}^{+}=5}$
indicates that the blanketing layer is an important feature of rough-wall flow at high values of
$\unicode[STIX]{x0394}U^{+}$
.
5 Discussion
Based on the observations in the previous sections, we can formulate the following scenario for the near-wall flow in the transitionally rough to fully rough region. This will be described in terms of the transformation of the viscous sublayer to a blanketing layer. To give some impression of the spatial distribution of the blanketing layer over the rough surface, the thickness of the blanketing layer
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}$
and the upper end of the blanketing layer
$z_{\overline{u}^{+}=5}$
are shown in figure 16 for the graphite surface and in figure 17 for the grit-blasted surface, at
$Re_{\unicode[STIX]{x1D70F}}=90$
,
$240$
and
$720$
. The blanketing layer clearly attains its highest thickness over the deepest cavities of the surface. The thickness of the blanketing layer decreases with increasing Reynolds number for most of the surface, with the exception of narrow cavities or areas that are shielded by higher roughness features. The upper end of the blanketing layer tends to move closer to the surface as the Reynolds number increases. This quantity shows clear streamwise structures that emerge in the blanketing layer with increasing Reynolds numbers: the blanketing layer tends to remain elevated above the surface for some distance behind larger roughness features; on the other hand, also deeper canyon-like structures form in the streamwise direction, where the flow can locally adapt very closely to the surface topography.
Figure 16. Graphite surface. (a–c) Rough surfaces coloured with thickness of blanketing layer at (a)
$Re_{\unicode[STIX]{x1D70F}}=90$
, (b)
$Re_{\unicode[STIX]{x1D70F}}=240$
and (c)
$Re_{\unicode[STIX]{x1D70F}}=720$
. (d–f) Location of upper end of blanketing layer at (d)
$Re_{\unicode[STIX]{x1D70F}}=90$
, (e)
$Re_{\unicode[STIX]{x1D70F}}=240$
and (f)
$Re_{\unicode[STIX]{x1D70F}}=720$
.
Figure 17. Grit-blasted surface. (a–c) Rough surfaces coloured with thickness of blanketing layer at (a)
$Re_{\unicode[STIX]{x1D70F}}=90$
, (b)
$Re_{\unicode[STIX]{x1D70F}}=240$
and (c)
$Re_{\unicode[STIX]{x1D70F}}=720$
. (d–f) Location of upper end of blanketing layer at (d)
$Re_{\unicode[STIX]{x1D70F}}=90$
, (e)
$Re_{\unicode[STIX]{x1D70F}}=240$
and (f)
$Re_{\unicode[STIX]{x1D70F}}=720$
.
In the low-
$Re_{\unicode[STIX]{x1D70F}}$
case the average roughness height
$S_{a}^{+}$
is lower than the thickness of the viscous sublayer of a corresponding smooth-wall flow. The rough-wall blanketing layer extends in most places above the height of the surface and still resembles a viscous sublayer (evidenced by the relatively narrow distribution found for the location of the upper end of the blanketing layer shown in figure 14). Disturbances of the blanket layer show long correlations in the streamwise direction (see figures 16
d and 17
d). Reversed flow can be found in the cavities of the surface but the magnitude is low.
As the Reynolds number increases, the roughness height exceeds the thickness of the viscous sublayer of a corresponding smooth-wall flow. The blanketing layer does not resemble a viscous sublayer any more – it has a wider height distribution. The reversed flow extends to higher heights, occurs for larger parts of the surface and intensifies. This reversed flow helps in smoothing out some of the surface features, so that the blanketing layer does not follow the deeper valleys of the surface. The higher reverse flow may cause a higher effective shear, which would explain the steep increase in roughness function with Reynolds number in the upper transitionally rough regime.
At high Reynolds numbers, the areas of reversed flow are ‘eroded’, i.e. reduced in height due to the high near-wall momentum in the upper part of the surface. The blanket layer increasingly adapts to the surface, which may be a consequence of the reduction of the streamwise length scale of the turbulent near-wall flow structures with Reynolds number. In the p.d.f. of thickness of the blanketing layer in inner units (see figure 15), a near-wall peak is sustained at
$\unicode[STIX]{x0394}D_{\overline{v}_{abs}^{+}=5}^{+}\approx 5$
, which indicates that patches of viscous sublayer exist even at higher Reynolds numbers where the flow is in the fully rough region. These patches occur typically at the windward parts of the crests of the highest roughness features of the surface (see figures 16
c and 17
c).
Figure 18. The p.d.f.s of the time-averaged r.m.s. velocity fluctuations attained at the upper end of the blanketing layer: (a,d) streamwise component; (b,e) spanwise component; and (c,f) wall-normal component. Panels (a–c) show data for the graphite surface; and panels (d–f) show data for the grit-blasted surface.
The statistics of the velocity fluctuations give further insight into the flow in the blanketing layer. Figure 18 shows values of the time-averaged r.m.s. velocity fluctuations attained at the upper end of the blanketing layer, i.e. at
$z_{u^{+}=5}$
. In the smooth-wall case, the r.m.s. velocity fluctuations at
$z^{+}=5$
attain values of
${\approx}1.5{-}1.8$
for the streamwise component,
${\approx}0.45{-}0.9$
for the spanwise component and
${\approx}0.15{-}0.25$
for the wall-normal component over the same range of Reynolds numbers (Hu, Morfey & Sandham Reference Hu, Morfey and Sandham2006). As the Reynolds number increases, the distribution of streamwise velocity fluctuations widens before it approaches (at the highest Reynolds number) an approximately constant shape. The peak values stay in the range 1.5–2, which is close to the values observed in the smooth-wall case. A different behaviour is observed for both the spanwise and wall-normal velocity fluctuations. Here the peak of the p.d.f.s moves to higher values with increasing Reynolds number, and the average values attained exceed the values in the smooth-wall case. Although the differences between the p.d.f.s diminish as the Reynolds number increases, for both the spanwise and wall-normal velocity fluctuations, the distributions exhibit significant Reynolds-number dependence at the highest Reynolds numbers studied, showing that the near-wall flow is still Reynolds-number-dependent. The observations made here for the growing intensity of the wall-normal velocity fluctuations are consistent with the results of the numerical experiments of Orlandi et al. (Reference Orlandi, Leonardi, Tuzi and Antonia2003) in the context of spanwise bar roughness, which showed that near-wall wall-normal velocity fluctuations play an important role in energising rough-wall turbulence.
Figure 19. The joint p.d.f.s of the time-averaged r.m.s. velocity fluctuations with blanketing layer thickness attained at
$Re_{\unicode[STIX]{x1D70F}}=720$
: (a,d) streamwise component; (b,e) spanwise component; and (c,f) wall-normal component. Panels (a–c) show data for the graphite surface; and panels (d–f) show data for the grit-blasted surface.
The p.d.f.s of the velocity fluctuations show significant variations across the blanketing layer. In figure 19 the joint probability distributions of the local time-averaged r.m.s. velocity fluctuations and the blanketing layer thickness are shown for the highest-Reynolds-number case
$Re_{\unicode[STIX]{x1D70F}}=720$
. High values of the velocity fluctuations are strongly correlated with high blanketing layer thickness. For all velocity components, the peak in the joint p.d.f. is located at low blanket layer thickness, where a peak was observed in the p.d.f. of the blanket layer thickness (see figure 15). Regarding the velocity fluctuations, the peak is located at
$\sqrt{\overline{u^{\prime 2}}}\approx 1.7$
for the streamwise,
$\sqrt{\overline{v^{\prime 2}}}\approx 1.0$
for the spanwise and
$\sqrt{\overline{w^{\prime 2}}}\approx 0.3$
for the wall-normal velocity components. These peak locations are close to the values for a smooth-wall viscous sublayer at
$z^{+}=5$
discussed above and therefore consistent with the hypothesis that patches of the viscous sublayer survive at higher Reynolds number.
Figure 20. Contours of the wall-normal component of the instantaneous vorticity
$\unicode[STIX]{x1D714}_{z}$
(red,
$+1\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D714}_{z}}$
; blue,
$-1\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D714}_{z}}$
) shown in the plane
$z/\unicode[STIX]{x1D6FF}=0.05$
for (a–c) the graphite surface and (d–f) the grit-blasted surface: (a,d)
$Re_{\unicode[STIX]{x1D70F}}=90$
; (b,e)
$Re_{\unicode[STIX]{x1D70F}}=240$
; and (c,f)
$Re_{\unicode[STIX]{x1D70F}}=720$
.
In a turbulent smooth-wall flow, the characteristic size of the near-wall structures, e.g. the low-speed streaks, is determined by the viscous length scale and not by outer units. For example, average streak length is estimated to be
$l_{streak}^{+}\approx 1000$
and spacing
${\approx}100$
(Smith & Metzler Reference Smith and Metzler1983; Chernyshenko & Baig Reference Chernyshenko and Baig2005). In a rough-wall flow, the roughness will disrupt the streak-like structures and thus significantly reduce their length (Orlandi & Leonardi Reference Orlandi and Leonardi2009; De Marchis et al.
Reference De Marchis, Napoli and Armenio2010). In figure 20, contours of the wall-normal component of the instantaneous vorticity field are shown for a plane in the upper part of the canopy. As can be observed, the size of the characteristic structures decreases with increasing Reynolds number, i.e. the size of the near-wall turbulence structures is still governed by the viscous length scale. Thus at higher Reynolds numbers, the near-wall turbulence structures are shorter compared to typical wavelengths of the roughness, allowing the flow to adapt more easily to the roughness topography.
In all cases the blanketing layer (see figures 16
d–f and 17
d–f) shows structures that are aligned with the streamwise direction of the flow, even though the rough surfaces do not have a preferred directionality. This observation can be related to the spanwise localised low-momentum and high-momentum pathways reported by Mejia-Alvarez & Christensen (Reference Mejia-Alvarez and Christensen2013), who conducted wind-tunnel measurements of turbulent boundary layer flow over irregular rough surfaces that also possessed no preferential direction. In the context of irregular rough surfaces, the existence of large-scale secondary flows is likely to be much more prevalent than for the traditionally studied rough surfaces consisting of regular arrays of roughness elements. Since irregular rough surfaces have structures over a wide range of scales rather than a single dominant scale, the coarseness criterion for the existence of large-scale secondary flows developed by Vanderwel & Ganapathisubramani (Reference Vanderwel and Ganapathisubramani2015), who proposed a minimum roughness spacing
$S/\unicode[STIX]{x1D6FF}>0.5$
for emergence of large-scale secondary flows, will be fulfilled in many cases if the spacing is based on the size of the largest surface structures.
6 Conclusions
In this work the aerodynamic properties of two different engineering rough surfaces have been studied. It was found that the roughness function is mainly affected by the highest peaks and lowest valleys of these surfaces, and thus the mean peak-to-valley height gives a better estimate for the equivalent sand-grain roughness than the mean roughness height. This distinction mainly matters for highly irregular rough surfaces, e.g. those generated by erosion processes, and not so much for rough surfaces with a more uniform height distribution, such as sandpaper surfaces of a given grain size. In agreement with previous experimental results, we found that positive skewness promotes a stronger aerodynamic roughness effect. However, the difference was not very pronounced – a
$33\,\%$
difference in equivalent sand-grain roughness was measured.
The near-wall flow over a rough surface undergoes a number of changes in the transitionally rough region. These were characterised in the present contribution by looking at the properties of the blanketing layer, the region of the flow in immediate vicinity to a rough wall. The blanketing layer can partially adapt to the rough surface, which is probably due to the higher near-wall momentum and the smaller size of turbulent near-wall structures as the Reynolds number is increased. The viscous sublayer is not fully destroyed and, for parts of the surface, patches of the viscous sublayer remain or re-emerge at higher Reynolds number. The exact transformation that the near-wall flow undergoes with increasing Reynolds number depends of course on the shape of the rough surface. The surfaces studied here are differentiable and have no steps or sharp peaks. They thus differ from the bar and cube roughness investigated in many previous studies of rough-wall turbulent flow. The differentiability of a rough surfaces (or the lack thereof) may be one of the reasons why there is no universal behaviour observed in the transitionally rough region. For the surfaces studied here, we observed a reduction in size and height extent of the areas of reversed flow in the upper transitionally rough region, which can be described as an ‘erosion’ of reversed flow areas. However, areas of reversed flow are not equally susceptible to this process. Reversed flow in areas with low local slopes is easier to eliminate than reversed flows that are tied to areas with very high local slope (or singularities in the local slope), since the blanketing layer can more easily adapt to a moderate slope. For surfaces with pronounced steps or very sharp peaks, behind which strongly separated flow can form (as for example in the backward-facing step case (Nadge & Govardhan Reference Nadge and Govardhan2014)), the reversed flow may be very difficult or even impossible to erode. They may thus display fully rough behaviour earlier than more smoothly varying rough surfaces where the near-wall flow has a much stronger Reynolds-number dependence, examples for which have been studied here.
Acknowledgements
This work has been supported by the Engineering and Physical Sciences Research Council grant nos EP/I032576/1 and EP/L000261/1. The authors acknowledge the use of the IRIDIS High Performance Computing Facility, and associated support services at the University of Southampton, in the completion of this work. Surface and velocity data are openly available from the University of Glasgow Enlighten repository under https://doi.org/10.5525/gla.researchdata.356.
Appendix A. Surface preparation
The irregular rough surfaces investigated in this study are based on samples of real engineering rough surfaces. The surface samples are scanned using an Alicona Infinite Focus microscope, which produces a two-dimensional map of the roughness height.
The raw surface data cannot be directly used for the DNS for several reasons. First, the measurement process entails measurement errors, which typically occur on small spatial scales. Secondly, the DNS of channel flow requires a surface that varies continuously across the periodic boundary conditions applied in the streamwise and spanwise directions. Finally, finite computational resources mean that extremely small surface features cannot be resolved in a simulation.
Therefore, the raw surface data are filtered by applying a circular low-pass filter in Fourier space,
$$\begin{eqnarray}f_{c}(k_{x},k_{y})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{ for }k_{x}^{2}+k_{y}^{2}\leqslant k_{c}^{2},\\ 0\quad & \text{ for }k_{x}^{2}+k_{y}^{2}>k_{c}^{2},\\ \quad \end{array}\right.\end{eqnarray}$$
i.e. the content of all modes
$(k_{x},k_{y})$
of the surface exceeding a cutoff wavenumber
$k_{c}$
are set to zero. The cutoff wavenumber is in general surface-dependent and needs to be chosen with care to ensure that the topographical parameters of the post-processed surface still retain the character of the original surface sample. For the current samples, a cutoff wavenumber of
$k_{c}=24/lx$
was chosen.
Some degree of post-processing and loss of small-scale features is inevitable in both simulations and experiments. In all cases, the acquisition of the surface data will to some extent be affected by measurement errors, and the employed measurement method may not be able to accurately capture the smallest scales of a surface. When reproducing a surface, e.g. for a wind-tunnel test, surface generation techniques such as moulding or three-dimensional printing will also struggle to faithfully reproduce very small scales. If larger areas are to be covered using a tiling process, the surface data will need to be post-processed to ensure that the tiles match up, forming a continuous surface. However, both experiments and simulations show that surface features on scales that are small compared to the dominant roughness scales have only weak influence on the fluid dynamic properties of rough-wall flow (Mejia-Alvarez & Christensen Reference Mejia-Alvarez and Christensen2010; Busse et al. Reference Busse, Lützner and Sandham2015).
Appendix B. Embedded boundary method
The iterative embedded boundary method used is a modified version of the embedded boundary method of Yang & Balaras (Reference Yang and Balaras2006). Full details and validation of the method can be found in Busse et al. (Reference Busse, Lützner and Sandham2015).
The basic principle of the method is the classification of all grid points in the simulation domain into solid points (which fall into the solid phase), fluid points (points in the fluid that have no adjacent solid point) and forcing points (points in the fluid that have at least one adjacent solid point). At solid points, the velocity is set to zero (corresponding to a solid/rough surface at rest). At fluid points, the discretised flow equations remain unmodified. At forcing points, the velocity is reconstructed based on neighbouring points in the fluid phase and the projection of the forcing point onto the surface. This is equivalent to the introduction of an extra force term
$\boldsymbol{f}_{emb}$
in the discretised flow equations at the forcing points.
Owing to the use of an embedded boundary method, the rough surface will not follow the distribution of the grid points. Therefore, it is more convenient to obtain the momentum balance for the streamwise component of the velocity using volume integrals instead of the more widely used surface integral formulation (Wang, Yeo & Khoo Reference Wang, Yeo and Khoo2006). The net skin friction drag per unit volume is given by
$$\begin{eqnarray}T_{x}=\frac{1}{V}\overline{\int _{V}\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}u_{1}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}\,\text{d}V}\end{eqnarray}$$
and the net form drag per unit volume by
$$\begin{eqnarray}F_{x}=\frac{1}{V}\overline{\int _{V}-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{1}}\,\text{d}V},\end{eqnarray}$$
where
$V$
is the volume occupied by the fluid, and the overline indicates averaging in time. At the forcing points, the non-zero effective embedded boundary force term contributes to the force balance. The rough-wall-parallel part of
$f_{emb,x}$
is included in the friction force and the rough-wall-normal part in the form drag.
Open access
