Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-28T00:59:05.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Richtmyer–Meshkov instability of an unperturbed interface subjected to a diffracted convergent shock

Published online by Cambridge University Press:  27 September 2019

Liyong Zou ,
Mahamad Al-Marouf ,
Wan Cheng Open the ORCID record for Wan Cheng [Opens in a new window] ,
Ravi Samtaney ,
Juchun Ding Open the ORCID record for Juchun Ding [Opens in a new window]  and
Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window]
Liyong Zou
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia Laboratory for Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China
Mahamad Al-Marouf
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
Wan Cheng*
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
Ravi Samtaney
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia
Juchun Ding
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Xisheng Luo*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
*
†Email addresses for correspondence: wan.cheng@kaust.edu.sa, xluo@ustc.edu.cn
†Email addresses for correspondence: wan.cheng@kaust.edu.sa, xluo@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

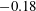The Richtmyer–Meshkov (RM) instability is numerically investigated on an unperturbed interface subjected to a diffracted convergent shock created by diffracting an initially cylindrical shock over a rigid cylinder. Four gas interfaces are considered with Atwood number ranging from $-0.18$ to 0.67. Results indicate that the diffracted convergent shock increases its strength gradually and reduces its amplitude quickly when it propagates towards the convergence centre. After the strike of the diffracted convergent shock, the initially unperturbed interface deforms with a bulge structure at the centre and two interface steps at both sides, which can be ascribed to the non-uniformity of the pressure distribution behind the diffracted convergent shock. With the decrease of Atwood number, the bulge structure becomes more pronounced. Quantitatively, the interface amplitude experiences a fast but short growing stage and then enters a linear stage. A good collapse of the dimensionless amplitude is found for all cases, which indicates a weak dependence of the growth rate on Atwood number in the deformed shock-induced RM instability. Then the impulsive theory is modified by eliminating the Atwood number and considering the geometry convergence, which well predicts the amplitude growth for the deformed shock-induced RM instability. Finally, the underlying mechanism is decoupled into three parts, and it is found that both the impulsive pressure perturbation and the geometry convergence promote the growth of interface perturbation while the continuous pressure perturbation inhibits the growth. As the Atwood number decreases, the impulsive perturbation plays an increasingly important role, which suggests that the impulsive perturbation dominates the deformed shock-induced RM instability at the linear stage.

JFM classification

Compressible Flows: Shock waves Instability: Nonlinear instability Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 448 - 467
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, M., Colella, P., Graves, D. T., Johnson, J. N., Johansen, H. S., Keen, N. D., Ligocki, T. J., Martin, D. F., McCorquodale, P. W., Modiano, D. et al. 2014 Chombo software package for AMR applications design document. Tech Rep. pp. 1–185. Lawrence Berkeley National Laboratory.Google Scholar
Al-Marouf, M. & Samtaney, R. 2017 A versatile embedded boundary adaptive mesh method for compressible flow in complex geometry. J. Comput. Phys. 337, 339–378.10.1016/j.jcp.2017.02.044Google Scholar
Apazidis, N. & Lesser, M. B. 1996 On generation and convergence of polygonal-shaped shock waves. J. Fluid Mech. 309, 301–319.10.1017/S0022112096001644Google Scholar
Aslam, T. 2004 A partial differential equation approach to multidimensional extrapolation. J. Comput. Phys. 193 (1), 349–355.10.1016/j.jcp.2003.08.001Google Scholar
Bell, G. I.1951 Taylor instability on cylinders and spheres in the small amplitude approximation. Tech Rep. LA-1321. Los Alamos National Laboratory.Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.10.1146/annurev.fluid.34.090101.162238Google Scholar
Chester, W. 1954 The quasi-cylindrical shock tube. Lond. Edin. Phil. Mag. J. Sci. 45, 1293–1301.10.1080/14786441208561138Google Scholar
Chisnell, R. F. 1957 The motion of a shock wave in a channel, with applications to cylindrical and spherical shock waves. J. Fluid Mech. 2, 286–298.10.1017/S0022112057000130Google Scholar
Colella, P. 1990 Multidimensional upwind methods for hyperbolic conservation laws. J. Comput. Phys. 87, 171–200.10.1016/0021-9991(90)90233-QGoogle Scholar
Dimotakis, P. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.10.1146/annurev.fluid.36.050802.122015Google Scholar
Dimotakis, P. E. & Samtaney, R. 2006 Planar shock cylindrical focusing by a perfect-gas lens. Phys. Fluids 18, 031705.10.1063/1.2186553Google Scholar
Ding, J., Si, T., Yang, J., Lu, X., Zhai, Z. & Luo, X. 2017 Measurement of a Richtmyer–Meshkov instability at an air-SF6 interface in a semiannular shock tube. Phys. Rev. Lett. 119 (1), 014501.10.1103/PhysRevLett.119.014501Google Scholar
Endo, T., Shigemori, K., Azechi, H., Nishiguchi, A., Mima, K., Sato, M., Nakai, M., Nakaji, S., Miyanaga, N., Matsuoka, S., Ando, A., Tanaka, K. A. & Nakai, S. 1995 Dynamic behavior of rippled shock waves and subsequently induced areal-density-perturbation growth in laser-irradiated foils. Phys. Rev. Lett. 74, 3608–3611.10.1103/PhysRevLett.74.3608Google Scholar
Franke, R. 1982 Scattered data interpolation: tests of some methods. Math. Comput. 38 (157), 181–200.Google Scholar
Hosseini, S. H. R. & Takayama, K. 2010 Experimental study of toroidal shock wave focusing in a compact vertical annular diaphragmless shock tube. Shock Waves 20, 1–7.10.1007/s00193-009-0227-5Google Scholar
Ishizaki, R. & Nishihara, K. 1997 Propagation of a rippled shock wave driven by nonuniform laser ablation. Phys. Rev. Lett. 78, 1920–1923.10.1103/PhysRevLett.78.1920Google Scholar
Ishizaki, R., Nishihara, K., Sakagami, H. & Ueshima, Y. 1996 Instability of a contact surface driven by a nonuniform shock wave. Phys. Rev. E 53(6), R5592.Google Scholar
Liang, Y., Ding, J., Zhai, Z., Si, T. & Luo, X. 2017 Interaction of cylindrically converging diffracted shock with uniform interface. Phys. Fluids 29 (8), 086101.10.1063/1.4997071Google Scholar
Liao, S., Zhang, W., Chen, H., Zou, L., Liu, J. & Zheng, X. 2019 Atwood number effects on the instability of a uniform interface driven by a perturbed shock wave. Phys. Rev. E 99, 013103.Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.10.1063/1.4865400Google Scholar
Lombardini, M. & Pullin, D. I. 2009 Small-amplitude perturbations in the three-dimensional cylindrical Richtmyer–Meshkov instability. Phys. Fluids 21, 114103.10.1063/1.3258668Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2014a Turbulent mixing driven by spherical implosions. Part 1. Flow description and mixing-layer growth. J. Fluid Mech. 748, 85.10.1017/jfm.2014.161Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2014b Turbulent mixing driven by spherical implosions. Part 2. Turbulence statistics. J. Fluid Mech. 748, 113–142.10.1017/jfm.2014.163Google Scholar
Luo, X., Ding, J., Wang, M., Zhai, Z. & Si, T. 2015 A semi-annular shock tube for studying cylindrically converging Richtmyer–Meshkov instability. Phys. Fluids 27(9), 091702.Google Scholar
Matsui, N., Mima, K., Honda, M. & Nishiguchi, A. 1999 Analysis of rippled shock-wave propagation and ablation-front stability by theory and hydrodynamic simulation. J. Plasma Phys. 61, 43–50.10.1017/S0022377898007260Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.Google Scholar
Mikaelian, K. O. 2005 Rayleigh–Taylor and Richtmyer–Meshkov instabilities and mixing in stratified cylindrical shells. Phys. Fluids 17, 094105.10.1063/1.2046712Google Scholar
Mostert, W., Pullin, D. I., Samtaney, R. & Wheatley, V. 2018a Singularity formation on perturbed planar shock waves. J. Fluid Mech. 846, 536–562.10.1017/jfm.2018.263Google Scholar
Mostert, W., Pullin, D. I., Samtaney, R. & Wheatley, V. 2018b Spontaneous singularity formation in converging cylindrical shock waves. Phys. Rev. Fluids 3, 071401(R).10.1103/PhysRevFluids.3.071401Google Scholar
Ortega, A. L., Lombardini, M., Barton, P. T., Pullin, D. I. & Meiron, D. I. 2015 Richtmyer–Meshkov instability for elastic-plastic solids in converging geometries. J. Mech. Phys. Solids 76, 291–324.10.1016/j.jmps.2014.12.002Google Scholar
Perry, R. W. & Kantrowitz, A. 1951 The production and stability of converging shock waves. J. Appl. Phys. 22, 878–885.10.1063/1.1700067Google Scholar
Plesset, M. S. 1954 On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.10.1063/1.1721529Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.10.1146/annurev-fluid-122109-160744Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.10.1002/cpa.3160130207Google Scholar
Samtaney, R. & Pullin, D. I. 1996 On initial-value and self-similar solutions of the compressible Euler equations. Phys. Fluids 10, 2650–2655.10.1063/1.869050Google Scholar
Takayama, K., Kleine, H. & Grönig, H. 1987 An experimental investigation of the stability of converging cylindrical shock waves in air. Exp. Fluids 5, 315.10.1007/BF00277710Google Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Thomas, V. A. & Kares, R. J. 2012 Drive asymmetry and the origin of turbulence in an ICF implosion. Phys. Rev. Lett. 109 (7), 075004.10.1103/PhysRevLett.109.075004Google Scholar
Vandenboomgaerde, M. & Aymard, C. 2011 Analytical theory for planar shock focusing through perfect gas lens and shock tube experiment designs. Phys. Fluids 23, 016101.10.1063/1.3549930Google Scholar
Vandenboomgaerde, M., Mügler, C. & Gauthier, S. 1998 Impulsive model for the Richtmyer–Meshkov instability. Phys. Rev. E 58, 1874–1882.Google Scholar
Vandenboomgaerde, M., Rouzier, P., Souffland, D., Biamino, L., Jourdan, G., Houas, L. & Mariani, C. 2018 Nonlinear growth of the converging Richtmyer–Meshkov instability in a conventional shock tube. Phys. Rev. Fluids 3, 014001.10.1103/PhysRevFluids.3.014001Google Scholar
Whitham, G. B. 1957 A new approach to problems of shock dynamics. Part 1. Two-dimensional problems. J. Fluid Mech. 2, 145–171.10.1017/S002211205700004XGoogle Scholar
Yang, J., Kubota, T. & Zukoski, E. E. 1993 Application of shock-induced mixing to supersonic combustion. AIAA J. 31, 854–862.10.2514/3.11696Google Scholar
Youngs, D. L. & Williams, R. J. 2008 Turbulent mixing in spherical implosions. Intl J. Numer. Meth. Fluids 56, 1597.10.1002/fld.1594Google Scholar
Zabusky, N. J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31, 495–536.10.1146/annurev.fluid.31.1.495Google Scholar
Zhai, Z., Liang, Y., Liu, L., Ding, J., Luo, X. & Zou, L. 2018a Interaction of rippled shock wave with flat fast–slow interface. Phys. Fluids 30, 046104.10.1063/1.5024774Google Scholar
Zhai, Z., Liu, C., Qin, F., Yang, J. & Luo, X. 2010 Generation of cylindrical converging shock waves based on shock dynamcis theory. Phys. Fluids 22, 041701.10.1063/1.3392603Google Scholar
Zhai, Z., Si, T., Luo, X., Yang, J., Liu, C., Tan, D. & Zou, L. 2012 Parametric study of cylindrical converging shock waves generated based on shock dynamics theory. Phys. Fluids 24, 026101.10.1063/1.3682376Google Scholar
Zhai, Z., Zou, L., Wu, Q. & Luo, X. 2018b Review of experimental Richtmyer–Meshkov instability in shock tube: from simple to complex. Proc. Inst. Mech. Engrs Part C 232 (16), 2830–2849.10.1177/0954406217727305Google Scholar
Zhang, W., Wu, Q., Zou, L., Zheng, X., Li, X., Luo, X. & Ding, J. 2018 Mach number effects on the instability of a planar interface subjected to a rippled shock. Phys. Rev. E 98, 043105.Google Scholar
Zhou, Y. 2017 Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar
Zou, L., Liu, J., Liao, S., Zheng, X., Zhai, Z. & Luo, X. 2017 Richtmyer–Meshkov instability of a flat interface subjected to a rippled shock wave. Phys. Rev. E 95, 013107.Google Scholar