Article contents
Rotating horizontal convection
Published online by Cambridge University Press: 16 April 2013
Abstract
‘Horizontal convection’ (HC) is the generic name for the flow resulting from a buoyancy variation imposed along a horizontal boundary of a fluid. We study the effects of rotation on three-dimensional HC numerically in two stages: first, when baroclinic instability is suppressed and, second, when it ensues and baroclinic eddies are formed. We concentrate on changes to the thickness of the near-surface boundary layer, the stratification at depth, the overturning circulation and the flow energetics during each of these stages. Our results show that, for moderate flux Rayleigh numbers ( 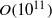 $O(1{0}^{11} )$ ), rapid rotation greatly alters the steady-state solution of HC. When the flow is constrained to be uniform in the transverse direction, rapidly rotating solutions do not support a boundary layer, exhibit weaker overturning circulation and greater stratification at all depths. In this case, diffusion is the dominant mechanism for lateral buoyancy flux and the consequent buildup of available potential energy leads to baroclinically unstable solutions. When these rapidly rotating flows are perturbed, baroclinic instability develops and baroclinic eddies dominate both the lateral and vertical buoyancy fluxes. The resulting statistically steady solution supports a boundary layer, larger values of deep stratification and multiple overturning cells compared with non-rotating HC. A transformed Eulerian-mean approach shows that the residual circulation is dominated by the quasi-geostrophic eddy streamfunction and that the eddy buoyancy flux has a non-negligible interior diabatic component. The kinetic and available potential energies are greater than in the non-rotating case and the mixing efficiency drops from
$O(1{0}^{11} )$ ), rapid rotation greatly alters the steady-state solution of HC. When the flow is constrained to be uniform in the transverse direction, rapidly rotating solutions do not support a boundary layer, exhibit weaker overturning circulation and greater stratification at all depths. In this case, diffusion is the dominant mechanism for lateral buoyancy flux and the consequent buildup of available potential energy leads to baroclinically unstable solutions. When these rapidly rotating flows are perturbed, baroclinic instability develops and baroclinic eddies dominate both the lateral and vertical buoyancy fluxes. The resulting statistically steady solution supports a boundary layer, larger values of deep stratification and multiple overturning cells compared with non-rotating HC. A transformed Eulerian-mean approach shows that the residual circulation is dominated by the quasi-geostrophic eddy streamfunction and that the eddy buoyancy flux has a non-negligible interior diabatic component. The kinetic and available potential energies are greater than in the non-rotating case and the mixing efficiency drops from 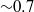 ${\sim }0. 7$ to
${\sim }0. 7$ to 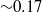 ${\sim }0. 17$ . The eddies play an important role in the formation of the thermal boundary layer and, together with the negatively buoyant plume, help establish deep stratification. These baroclinically active solutions have characteristics of geostrophic turbulence.
${\sim }0. 17$ . The eddies play an important role in the formation of the thermal boundary layer and, together with the negatively buoyant plume, help establish deep stratification. These baroclinically active solutions have characteristics of geostrophic turbulence.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 30
- Cited by

