Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-15T07:47:41.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Saturation of equatorial inertial instability

Published online by Cambridge University Press:  20 February 2015

R. C. Kloosterziel ,
P. Orlandi  and
G. F. Carnevale
R. C. Kloosterziel
Affiliation:
School of Ocean and Earth Science and Technology, University of Hawaii, Honolulu, HI 96822, USA Royal Netherlands Institute for Sea Research, PO Box 59, 1790 AB Texel, The Netherlands
P. Orlandi
Affiliation:
Dipartimento di Meccanica e Aeronautica, University of Rome, ‘La Sapienza’, via Eudossiana 18, 00184 Roma, Italy
G. F. Carnevale*
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 92093, USA
*
†Email address for correspondence: gcarnevale@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Inertial instability in parallel shear flows and circular vortices in a uniformly rotating system ( 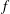$f$-plane) redistributes absolute linear momentum or absolute angular momentum in such a way as to neutralize the instability. In previous studies we showed that, in the absence of other instabilities, at high Reynolds numbers the final equilibrium can be predicted with a simple construction based on conservation of total momentum. In this paper we continue this line of research with a study of barotropic shear flows on the equatorial 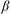${\it\beta}$-plane. Through numerical simulations the evolution of the instability is studied in select illuminating cases: a westward flowing Gaussian jet with the flow axis exactly on the equator, a uniform shear flow and eastward and westward flowing jets that have their flow axis shifted away from the equator. In the numerical simulations it is assumed that there are no along-stream variations. This suppresses equatorial Rossby waves and barotropic shear instabilities and allows only inertial instability to develop. We investigate whether for these flows on the equatorial 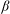${\it\beta}$-plane the final equilibrated flow can be predicted as was possible for flows on the 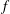$f$-plane. For the Gaussian jet centred on the equator the prediction of the equilibrated flow is obvious by mere inspection of the initial momentum distribution and by assuming that momentum is mixed and homogenized to render the equilibrated flow inertially stable. For the uniform shear flow, however, due to the peculiar nature of the initial momentum distribution and the fact that the Coriolis parameter 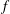$f$ varies with latitude, it appears that, unlike in our earlier studies of flows on the 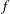$f$-plane, additional constraints need to be considered to correctly predict the outcome of the highly nonlinear evolution of the instability. The mixing range of the linear shear flow and the value of the mixed momentum is determined numerically and this is used to predict the equilibrated flow that emerges from an eastward flowing jet that is shifted a small distance away from the equator. For shifts large enough to induce no shear at the equator the equilibrium flow can be well predicted using the simple recipe used in our earlier studies of parallel shear flows on the 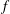$f$-plane. For the westward flowing jet shifted a very small distance from the equator, no prediction appears feasible. For modestly small shifts a prediction is possible by combining the empirical prediction for the linear shear flow with a prediction similar to what we used in our previous studies for flows on the 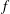$f$-plane.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Instability: Instability Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 562 - 594
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Bouchut, F., Ribstein, B. & Zeitlin, V. 2011 Inertial, barotropic, and baroclinic instabilities of the bickley jet in two-layer rotating shallow water model. Phys. Fluids 23, 126601.Google Scholar
Carnevale, G. F., Kloosterziel, R. C. & Orlandi, P. 2013 Inertial and barotropic instabilities of a free current in 3d rotating flow. J. Fluid Mech. 725, 117–151.Google Scholar
Carnevale, G. F., Kloosterziel, R. C., Orlandi, P. & van Sommeren, D. D. J. A. 2011 Predicting the aftermath of vortex breakup in rotating flow. J. Fluid Mech. 669, 90–119.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dunkerton, T. J. 1981 On the inertial instability of the equatorial middle atmosphere. J. Atmos. Sci. 38, 2354–2364.Google Scholar
Fjortoft, R. 1950 Application of integral theorems in deriving criteria of stability for laminar flows and for the baroclinic circular vortex. Geofys. Publ. 17, 1–52.Google Scholar
Gallaire, F. & Chomaz, J. M. 2003 Three-dimensional instability of isolated vortices. Phys. Fluids 15 (8), 2113–2126.Google Scholar
Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46, 1–33.Google Scholar
Griffiths, S. D. 2003a The nonlinear evolution of zonally symmetric equatorial inertial instability. J. Fluid Mech. 474, 245–273.Google Scholar
Griffiths, S. D. 2003b Nonlinear vertical scale selection in equatorial inertial instability. J. Atmos. Sci. 60, 977–990.Google Scholar
Griffiths, S. D. 2008 The limiting form of inertial instability in geophysical flows. J. Fluid Mech. 605, 115–143.CrossRefGoogle Scholar
Holton, J. R. 1992 An Introduction to Dynamic Meteorology, 3rd edn. Academic.Google Scholar
Hoskins, B. J. 1974 The role of potential vorticity in symmetric stability and instability. Q. J. R. Meteorol. Soc. 100, 480–482.Google Scholar
Kloosterziel, R. C. 2010 Viscous symmetric instabiliy of circular flows. J. Fluid Mech. 652, 171–193.CrossRefGoogle Scholar
Kloosterziel, R. C. & Carnevale, G. F. 2007 Generalized energetics for inertially stable parallel shear flows. J. Fluid Mech. 585, 117–126.Google Scholar
Kloosterziel, R. C. & Carnevale, G. F. 2008 Vertical scale selection in inertial instability. J. Fluid Mech. 594, 249–269.Google Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007a Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.Google Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2007b Saturation of inertial instability in rotating planar shear flows. J. Fluid Mech. 583, 413–422.Google Scholar
Kloosterziel, R. C. & van Heijst, G. J. F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.CrossRefGoogle Scholar
Ooyama, K. 1966 On the stability of the baroclinic circular vortex: a sufficient condition for instability. J. Atmos. Sci. 23, 43–53.Google Scholar
Orlandi, P. 2000 Fluid Flow Phenomena: A Numerical Toolkit. Kluwer.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21, 106601.Google Scholar
Rayleigh, Lord 1916 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Ribstein, B., Plougonven, R. & Zeitlin, V. 2014 Inertial versus baroclinic instability of the bickley jet in a continuously stratified rotating fluid. J. Fluid Mech. 743, 1–31.Google Scholar
Sawyer, S. J. 1947 Notes on the theory of tropical cyclones. Q. J. R. Meteorol. Soc. 73, 101–126.Google Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. J. Theor. Comput. Fluid Dyn. 11, 305–322.Google Scholar