Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-23T05:53:02.796Z Has data issue: false hasContentIssue false
  • English
  • Français

Selective energy and enstrophy modification of two-dimensional decaying turbulence

Published online by Cambridge University Press:  31 January 2023

Aditya G. Nair Open the ORCID record for Aditya G. Nair [Opens in a new window] ,
James Hanna  and
Matteo Aureli Open the ORCID record for Matteo Aureli [Opens in a new window]
Aditya G. Nair*
Affiliation:
Department of Mechanical Engineering, University of Nevada, Reno, NV 89557, USA
James Hanna
Affiliation:
Department of Mechanical Engineering, University of Nevada, Reno, NV 89557, USA
Matteo Aureli
Affiliation:
Department of Mechanical Engineering, University of Nevada, Reno, NV 89557, USA
*
†Email address for correspondence: adityan@unr.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

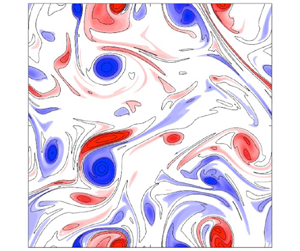
In two-dimensional decaying homogeneous isotropic turbulence, kinetic energy and enstrophy are respectively transferred to larger and smaller scales. In such spatiotemporally complex dynamics, it is challenging to identify the important flow structures that govern this behaviour. We propose and employ numerically two flow-modification strategies that leverage the inviscid global conservation of energy and enstrophy to design external forcing inputs that change these quantities selectively and simultaneously, and drive the system towards steady-state or other late-stage behaviour. One strategy employs only local flow field information, while the other is global. We observe various flow structures excited by these inputs and compare them with recent literature. Energy modification is characterized by the excitation of smaller wavenumber structures in the flow than enstrophy modification.

JFM classification

Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 956 , 10 February 2023 , A12
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aureli, M. & Hanna, J.A. 2021 Exterior dissipation, proportional decay, and integrals of motion. Phys. Rev. Lett. 127, 134101.CrossRefGoogle ScholarPubMed
Boffetta, G. & Ecke, R.E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.CrossRefGoogle Scholar
Bracco, A., McWilliams, J.C., Murante, G., Provenzale, A. & Weiss, J.B. 2000 Revisiting freely decaying two-dimensional turbulence at millennial resolution. Phys. Fluids 12 (11), 2931–2941.CrossRefGoogle Scholar
Davidson, P.A. 2015 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.CrossRefGoogle Scholar
Foias, C., Manley, O., Rosa, R. & Temam, R. 2001 Navier–Stokes Equations and Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Fox, S. & Davidson, P.A. 2010 Freely decaying two-dimensional turbulence. J. Fluid Mech. 659, 351.CrossRefGoogle Scholar
Gay-Balmaz, F. & Holm, D.D. 2013 Selective decay by Casimir dissipation in inviscid fluids. Nonlinearity 26 (2), 495.CrossRefGoogle Scholar
Hanna, J.A. 2021 An integrable family of torqued, damped, rigid rotors. Mech. Res. Commun. 116, 103768.CrossRefGoogle Scholar
Hasegawa, A. 1985 Self-organization processes in continuous media. Adv. Phys. 34 (1), 1–42.CrossRefGoogle Scholar
Holmes, P., Lumley, J.L., Berkooz, G. & Rowley, C.W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows. In Center for Turbulence Research Report CTR-S88, pp. 193–208.Google Scholar
Jiménez, J. 2020 a Dipoles and streams in two-dimensional turbulence. J. Fluid Mech. 904, A39.CrossRefGoogle Scholar
Jiménez, J. 2020 b Monte Carlo science. J. Turbul. 21 (9–10), 544–566.CrossRefGoogle Scholar
Kraichnan, R.H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.CrossRefGoogle Scholar
McWilliams, J.C. 1990 A demonstration of the suppression of turbulent cascades by coherent vortices in two-dimensional turbulence. Phys. Fluids A 2 (4), 547–552.CrossRefGoogle Scholar
Morrison, P.J. 1986 A paradigm for joined Hamiltonian and dissipative systems. Physica D 18 (1–3), 410–419.CrossRefGoogle Scholar
Oetzel, K.G. & Vallis, G.K. 1997 Strain, vortices, and the enstrophy inertial range in two-dimensional turbulence. Phys. Fluids 9 (10), 2991–3004.CrossRefGoogle Scholar
Sadourny, R. & Basdevant, C. 1985 Parameterization of subgrid scale barotropic and baroclinic eddies in quasi-geostrophic models: anticipated potential vorticity method. J. Atmos. Sci. 42 (13), 1353–1363.2.0.CO;2>CrossRefGoogle Scholar
Shepherd, T.G. 1990 A general method for finding extremal states of Hamiltonian dynamical systems, with applications to perfect fluids. J. Fluid Mech. 213 (1), 573–587.CrossRefGoogle Scholar
Smith, L.M. & Yakhot, V. 1993 Bose condensation and small-scale structure generation in a random force driven 2D turbulence. Phys. Rev. Lett. 71 (3), 352.CrossRefGoogle Scholar
Taira, K., Nair, A.G. & Brunton, S.L. 2016 Network structure of two-dimensional decaying isotropic turbulence. J. Fluid Mech. 795, R2.CrossRefGoogle Scholar
Vallis, G.K., Carnevale, G.F. & Young, W.R. 1989 Extremal energy properties and construction of stable solutions of the Euler equations. J. Fluid Mech. 207, 133–152.CrossRefGoogle Scholar
Vallis, G.K. & Hua, B. 1988 Eddy viscosity of the anticipated potential vorticity method. J. Atmos. Sci. 45 (4), 617–627.2.0.CO;2>CrossRefGoogle Scholar
Weiss, J. 1991 The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48 (2–3), 273–294.CrossRefGoogle Scholar
Yeh, C., Meena, M.G. & Taira, K. 2021 Network broadcast analysis and control of turbulent flows. J. Fluid Mech. 910, A15.CrossRefGoogle Scholar