Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marusic, Ivan
Baars, Woutijn J.
and
Hutchins, Nicholas
2017.
Scaling of the streamwise turbulence intensity in the context of inner-outer interactions in wall turbulence.
Physical Review Fluids,
Vol. 2,
Issue. 10,
Mizuno, Yoshinori
Yagi, Toshimasa
and
Mori, Kazuyasu
2018.
Contribution of attached eddies to the intensity and turbulent transfer of velocity fluctuations in wall-turbulence.
Fluid Dynamics Research,
Vol. 50,
Issue. 4,
p.
045513.
Hwang, Jinyul
and
Sung, Hyung Jin
2018.
Wall-attached structures of velocity fluctuations in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 856,
Issue. ,
p.
958.
Solak, Ilkay
and
Laval, Jean-Philippe
2018.
Large-scale motions from a direct numerical simulation of a turbulent boundary layer.
Physical Review E,
Vol. 98,
Issue. 3,
Wang, Wenkang
Pan, Chong
and
Wang, Jinjun
2018.
Wall-Normal Variation of Spanwise Streak Spacing in Turbulent Boundary Layer With Low-to-Moderate Reynolds Number.
Entropy,
Vol. 21,
Issue. 1,
p.
24.
Cho, Minjeong
Hwang, Yongyun
and
Choi, Haecheon
2018.
Scale interactions and spectral energy transfer in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
474.
Ganapathisubramani, B.
2018.
Law of the wall for small-scale streamwise turbulence intensity in high-Reynolds-number turbulent boundary layers.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Krug, Dominik
Baars, Woutijn J.
Hutchins, Nicholas
and
Marusic, Ivan
2019.
Vertical Coherence of Turbulence in the Atmospheric Surface Layer: Connecting the Hypotheses of Townsend and Davenport.
Boundary-Layer Meteorology,
Vol. 172,
Issue. 2,
p.
199.
Marusic, Ivan
and
Monty, Jason P.
2019.
Attached Eddy Model of Wall Turbulence.
Annual Review of Fluid Mechanics,
Vol. 51,
Issue. 1,
p.
49.
Vadarevu, Sabarish B.
Symon, Sean
Illingworth, Simon J.
and
Marusic, Ivan
2019.
Coherent structures in the linearized impulse response of turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
1190.
McKeon, Beverley J.
2019.
Self-similar hierarchies and attached eddies.
Physical Review Fluids,
Vol. 4,
Issue. 8,
Baidya, R.
Baars, W. J.
Zimmerman, S.
Samie, M.
Hearst, R. J.
Dogan, E.
Mascotelli, L.
Zheng, X.
Bellani, G.
Talamelli, A.
Ganapathisubramani, B.
Hutchins, N.
Marusic, I.
Klewicki, J.
and
Monty, J. P.
2019.
Simultaneous skin friction and velocity measurements in high Reynolds number pipe and boundary layer flows.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
377.
Madhusudanan, Anagha
Illingworth, Simon. J.
and
Marusic, Ivan
2019.
Coherent large-scale structures from the linearized Navier–Stokes equations.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
89.
Zhu, Hang-Yu
Pan, Chong
Wang, Jin-Jun
Liang, Yi-Rui
and
Ji, Xiao-Cang
2019.
Sand-turbulence interaction in a high-Reynolds-number turbulent boundary layer under net sedimentation conditions.
International Journal of Multiphase Flow,
Vol. 119,
Issue. ,
p.
56.
Deshpande, Rahul
Monty, Jason P.
and
Marusic, Ivan
2019.
Streamwise inclination angle of large wall-attached structures in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
Basley, Jérémy
Perret, Laurent
and
Mathis, Romain
2019.
Structure of high Reynolds number boundary layers over cube canopies.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
460.
Baars, Woutijn J.
and
Marusic, Ivan
2020.
Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra.
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
Deshpande, Rahul
Chandran, Dileep
Monty, Jason P.
and
Marusic, Ivan
2020.
Two-dimensional cross-spectrum of the streamwise velocity in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 890,
Issue. ,
Tanarro, Á.
Vinuesa, R.
and
Schlatter, P.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
11.
2020.
Characteristics of wall-attached motions in open channel flows.
Physics of Fluids,
Vol. 32,
Issue. 5,
p.
055110.
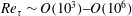 $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3}){-}O(10^{6})$ . Within each dataset, a self-similar structure is identified from the coherence between the turbulence in the logarithmic region and at the near-wall reference position. This self-similarity is described by a streamwise/wall-normal aspect ratio of
$Re_{\unicode[STIX]{x1D70F}}\sim O(10^{3}){-}O(10^{6})$ . Within each dataset, a self-similar structure is identified from the coherence between the turbulence in the logarithmic region and at the near-wall reference position. This self-similarity is described by a streamwise/wall-normal aspect ratio of 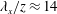 $\unicode[STIX]{x1D706}_{x}/z\approx 14$ , where
$\unicode[STIX]{x1D706}_{x}/z\approx 14$ , where 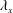 $\unicode[STIX]{x1D706}_{x}$ and
$\unicode[STIX]{x1D706}_{x}$ and  $z$ are the streamwise wavelength and wall-normal distance respectively.
$z$ are the streamwise wavelength and wall-normal distance respectively.

