Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Grue, John
2017.
Ship generated mini-tsunamis – CORRIGENDUM.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
962.
O'Brien, Laura
Renzi, Emiliano
Dudley, John M.
Clancy, Colm
and
Dias, Frédéric
2018.
Catalogue of extreme wave events in Ireland: revised and updated for 14 680 BP to 2017.
Natural Hazards and Earth System Sciences,
Vol. 18,
Issue. 3,
p.
729.
Macfarlane, G. J.
and
Graham-Parker, K. J.
2019.
Marine Vessel Wave Wake: Transient Effects When Accelerating or Decelerating.
Journal of Waterway, Port, Coastal, and Ocean Engineering,
Vol. 145,
Issue. 1,
Liang, Hui
and
Chen, Xiaobo
2019.
Viscous effects on the fundamental solution to ship waves.
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
p.
744.
Grue, John
2020.
Mini-Tsunami Made by Ship Moving Across a Depth Change.
Journal of Waterway, Port, Coastal, and Ocean Engineering,
Vol. 146,
Issue. 5,
Yuan, Peiyin
Wang, Pingyi
and
Zhao, Yu
2020.
Study on the Steepness of Landslide-Induced Wave and Nonlinear Motion of Container Ships.
Applied Sciences,
Vol. 10,
Issue. 6,
p.
2159.
Wang, Qian
Fang, Yongliu
and
Liu, Hua
2021.
An experimental study of run-up and loads on a vertical truncated cylinder in a solitary wave.
Ocean Engineering,
Vol. 219,
Issue. ,
p.
108346.
Terziev, Momchil
Tezdogan, Tahsin
and
Incecik, Atilla
2021.
Modelling the hydrodynamic effect of abrupt water depth changes on a ship travelling in restricted waters using CFD.
Ships and Offshore Structures,
Vol. 16,
Issue. 10,
p.
1087.
Lo, Peter H.-Y.
2021.
Approximate ship wake solution for fast computation.
Ocean Engineering,
Vol. 235,
Issue. ,
p.
109405.
Wang, Ping
and
Cheng, Jun
2021.
Mega-Ship-Generated Tsunami: A Field Observation in Tampa Bay, Florida.
Journal of Marine Science and Engineering,
Vol. 9,
Issue. 4,
p.
437.
Grue, John
Pedersen, Geir K.
and
Saetra, Øyvind
2022.
Free Wave Effects in Meteotsunamis.
Journal of Geophysical Research: Oceans,
Vol. 127,
Issue. 2,
Sun, Xiaofeng
Cai, Miaoyu
Wang, Jingkui
and
Liu, Chunlei
2022.
Numerical Simulation of the Kelvin Wake Patterns.
Applied Sciences,
Vol. 12,
Issue. 12,
p.
6265.
Shi, Kaiyuan
Zhu, Renchuan
Gu, Mengxiao
and
Wang, Xiaocong
2022.
Simulations of nonlinear waves generated by an air-cushion vehicle.
Ocean Engineering,
Vol. 253,
Issue. ,
p.
111181.
Azevedo, Laura
Meyers, Steven
Pleskachevsky, Andrey
Pereira, Henrique P. P.
and
Luther, Mark
2022.
Characterizing Rogue Waves at the Entrance of Tampa Bay (Florida, USA).
Journal of Marine Science and Engineering,
Vol. 10,
Issue. 4,
p.
507.
Ai, Congfang
Ma, Yuxiang
Sun, Lei
and
Dong, Guohai
2023.
Numerical simulation of ship waves in the presence of a uniform current.
Coastal Engineering,
Vol. 179,
Issue. ,
p.
104250.
Li, Mingxin
Yuan, Zhi-Ming
and
Tao, Longbin
2023.
Wash waves generated by ship moving across a depth change.
Ocean Engineering,
Vol. 275,
Issue. ,
p.
114073.
Shi, Hui
Luo, Yao
Zhou, Fenghua
Qiu, Chunhua
Wang, Dongxiao
and
Zhang, Zhenqiu
2023.
Abnormal Waves Observation and Analysis of the Mechanism in the Pearl River Estuary, South China.
Water,
Vol. 15,
Issue. 5,
p.
1001.
Liu, Y H
and
Terziev, M
2023.
Shallow waters resistance of an accelerating ship.
IOP Conference Series: Materials Science and Engineering,
Vol. 1288,
Issue. 1,
p.
012046.
Yao, Jinyu
Bingham, Harry B.
and
Zhang, Xinshu
2023.
Nonlinear effects of variable bathymetry and free surface on mini-tsunamis generated by a moving ship.
Physical Review Fluids,
Vol. 8,
Issue. 9,
Li, Ming-xin
Yuan, Zhi-ming
Bai, Xu
Li, Yong-zheng
Cheng, Yong
and
Tao, Long-bin
2023.
Numerical Modelling of Wash Waves Generated by Ships Moving over An Uneven Bottom.
China Ocean Engineering,
Vol. 37,
Issue. 1,
p.
145.
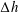 $\unicode[STIX]{x0394}h$ comparable to the average and relatively shallow water depth
$\unicode[STIX]{x0394}h$ comparable to the average and relatively shallow water depth 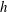 $h$ at the location, with
$h$ at the location, with 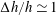 $\unicode[STIX]{x0394}h/h\simeq 1$ . The phenomenon is new and the waves were recently observed in the Oslofjord in Norway. The 0.5–1 km long waves, extending across the 2–3 km wide fjord, are observed as run-ups and run-downs along the shore, with periods of 30–60 s, where a wave height up to 1.4 m has been measured. The waves travelling with the shallow water speed, found ahead of the ships moving at subcritical depth Froude number, behave like a mini-tsunami. A qualitative explanation of the linear generation mechanism is provided by an asymptotic analysis, valid for
$\unicode[STIX]{x0394}h/h\simeq 1$ . The phenomenon is new and the waves were recently observed in the Oslofjord in Norway. The 0.5–1 km long waves, extending across the 2–3 km wide fjord, are observed as run-ups and run-downs along the shore, with periods of 30–60 s, where a wave height up to 1.4 m has been measured. The waves travelling with the shallow water speed, found ahead of the ships moving at subcritical depth Froude number, behave like a mini-tsunami. A qualitative explanation of the linear generation mechanism is provided by an asymptotic analysis, valid for  $\unicode[STIX]{x0394}h/h\ll 1$ and long waves, expressing the generation in terms of a pressure impulse at the depth change. Complementary fully dispersive calculations for
$\unicode[STIX]{x0394}h/h\ll 1$ and long waves, expressing the generation in terms of a pressure impulse at the depth change. Complementary fully dispersive calculations for 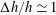 $\unicode[STIX]{x0394}h/h\simeq 1$ document symmetries of the waves at positive or negative
$\unicode[STIX]{x0394}h/h\simeq 1$ document symmetries of the waves at positive or negative 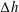 $\unicode[STIX]{x0394}h$ . The wave height grows with the ship speed
$\unicode[STIX]{x0394}h$ . The wave height grows with the ship speed 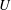 $U$ according to
$U$ according to 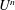 $U^{n}$ with
$U^{n}$ with  $n$ in the range 3–4, for
$n$ in the range 3–4, for 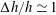 $\unicode[STIX]{x0394}h/h\simeq 1$ , while the growth in
$\unicode[STIX]{x0394}h/h\simeq 1$ , while the growth in 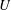 $U$ is only very weak for
$U$ is only very weak for 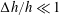 $\unicode[STIX]{x0394}h/h\ll 1$ (the asymptotics). Calculations show good agreement with observations.
$\unicode[STIX]{x0394}h/h\ll 1$ (the asymptotics). Calculations show good agreement with observations.