Article contents
Singularity formation on perturbed planar shock waves
Published online by Cambridge University Press: 08 May 2018
Abstract
We present an analysis that predicts the time to development of a singularity in the shape profile of a spatially periodic perturbed, planar shock wave for ideal gas dynamics. Beginning with a formulation in complex coordinates of Whitham’s approximate model geometrical shock dynamics (GSD), we apply a spectral treatment to derive the asymptotic form for the leading-order behaviour of the shock Fourier coefficients for large mode numbers and time. This is shown to determine a critical time at which the coefficients begin to decay, with respect to mode number, at an algebraic rate with an exponent of 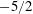 $-5/2$ , indicating loss of analyticity and the formation of a singularity in the shock geometry. The critical time is found to be inversely proportional to a representative measure of perturbation amplitude
$-5/2$ , indicating loss of analyticity and the formation of a singularity in the shock geometry. The critical time is found to be inversely proportional to a representative measure of perturbation amplitude  $\unicode[STIX]{x1D716}$ with an explicit analytic form for the constant of proportionality in terms of gas and shock parameters. To leading order, the time to singularity formation is dependent only on the first Fourier mode. Comparison with results of numerical solutions to the full GSD equations shows that the predicted critical time somewhat underestimates the time for shock–shock (triple-point) formation, where the latter is obtained by post-processing the numerical GSD results using an edge-detection algorithm. Aspects of the analysis suggest that the appearance of loss of analyticity in the shock surface may be a precursor to the first appearance of shock–shocks, which may account for part of the discrepancy. The frequency of oscillation of the shock perturbation is accurately predicted. In addition, the analysis is extended to the evolution of a perturbed planar, fast magnetohydrodynamic shock for the case when the external magnetic field is aligned parallel to the unperturbed shock. It is found that, for a strong shock, the presence of the magnetic field produces only a higher-order correction to the GSD equations with the result that the time to loss of analyticity is the same as for the gas-dynamic flow. Limitations and improvements for the analysis are discussed, as are comparisons with the analogous appearance of singularity formation in vortex-sheet evolution in an incompressible inviscid fluid.
$\unicode[STIX]{x1D716}$ with an explicit analytic form for the constant of proportionality in terms of gas and shock parameters. To leading order, the time to singularity formation is dependent only on the first Fourier mode. Comparison with results of numerical solutions to the full GSD equations shows that the predicted critical time somewhat underestimates the time for shock–shock (triple-point) formation, where the latter is obtained by post-processing the numerical GSD results using an edge-detection algorithm. Aspects of the analysis suggest that the appearance of loss of analyticity in the shock surface may be a precursor to the first appearance of shock–shocks, which may account for part of the discrepancy. The frequency of oscillation of the shock perturbation is accurately predicted. In addition, the analysis is extended to the evolution of a perturbed planar, fast magnetohydrodynamic shock for the case when the external magnetic field is aligned parallel to the unperturbed shock. It is found that, for a strong shock, the presence of the magnetic field produces only a higher-order correction to the GSD equations with the result that the time to loss of analyticity is the same as for the gas-dynamic flow. Limitations and improvements for the analysis are discussed, as are comparisons with the analogous appearance of singularity formation in vortex-sheet evolution in an incompressible inviscid fluid.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 11
- Cited by


