Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-24T06:40:49.135Z Has data issue: false hasContentIssue false
  • English
  • Français

A slender drop in a nonlinear extensional flow

Published online by Cambridge University Press:  02 November 2016

Moshe Favelukis
Moshe Favelukis*
Affiliation:
Department of Chemical Engineering, Shenkar – College of Engineering and Design, Ramat-Gan 5252626, Israel
*
†Email address for correspondence: favelukis@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The deformation of a slender drop in a nonlinear axisymmetric extensional and creeping flow has been theoretically studied. This problem, which was first suggested by Sherwood (J. Fluid Mech., vol. 144, 1984, pp. 281–295), is being revisited, and new results are presented. The problem is governed by three dimensionless parameters: the capillary number (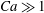$\mathit{Ca}\gg 1$), the viscosity ratio (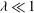$\unicode[STIX]{x1D706}\ll 1$), and the nonlinear intensity of the flow (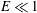$E\ll 1$). Contrary to linear extensional flow (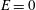$E=0$), where the local radius of the drop decreases monotonically (in the positive $z$ direction), in a nonlinear extensional flow (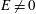$E\neq 0$), two possible steady shapes exist: steady shapes (stable or unstable) with the local radius decreasing monotonically, and steady shapes (unstable) where the local radius of the drop has a local maximum, besides the one at the centre of the drop. Similar to linear extensional flow, the addition of nonlinear extensional effects does not change the end shape of the steady drop, which has pointed ends. A stability analysis has been done to distinguish between stable and unstable steady shapes and to determine the breakup point. Time-dependent studies reveal three types of breakup mechanism: a centre pinching mode, indefinite elongation, and a mechanism that remind us of tip-streaming, where a cusp is developed at the end of the drop.

JFM classification

Drops and Bubbles: Drops and Bubbles Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Slender-body theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 337 - 361
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Lo, T. S. 1978 Deformation and breakup of a single slender drop in an extensional flow. J. Fluid. Mech. 86, 641–672.Google Scholar
Antanovskii, L. K. 1996 Formation of a pointed drop in Taylor’s four-roller mill. J. Fluid. Mech. 327, 325–341.CrossRefGoogle Scholar
Bentley, B.J. & Leal, L. G. 1986 An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech. 167, 241–283.Google Scholar
Booty, M. R. & Siegel, M. 2005 Steady deformation and tip-streaming of a slender bubble with surfactant in an extensional flow. J. Fluid Mech. 544, 243–275.Google Scholar
Brady, J. F. & Acrivos, A. 1982 The deformation and breakup of a slender drop in an extensional flow: inertial effects. J. Fluid Mech. 115, 443–451.Google Scholar
Briscoe, B. J., Lawrence, C. J. & Mietus, W. G. P. 1999 A review of immiscible fluid mixing. Adv. Colloid Interface Sci. 81, 1–17.Google Scholar
Buckmaster, J. D. 1972 Pointed bubbles in slow viscous flow. J. Fluid. Mech. 55, 385–400.CrossRefGoogle Scholar
Buckmaster, J. D. 1973 The bursting of pointed drops in slow viscous flow. J. Appl. Mech. E 40, 18–24.Google Scholar
De Bruijn, R. A. 1993 Tipstreaming of drops in simple shear flows. Chem. Engng Sci. 48, 277–284.Google Scholar
Eggleton, C. D., Tsai, T.-M. & Stebe, K. J. 2001 Tip streaming from a drop in the presence of surfactants. Phys. Rev. Lett. 87, 048302.Google Scholar
Favelukis, M., Lavrenteva, O. M. & Nir, A. 2005 Deformation and breakup of a non-Newtonian slender drop in an extensional flow. J. Non-Newtonian Fluid Mech. 125, 49–59.Google Scholar
Favelukis, M., Lavrenteva, O. M. & Nir, A. 2006 Deformation and breakup of a non-Newtonian slender drop in an extensional flow: inertial effects and stability. J. Fluid Mech. 563, 133–158.Google Scholar
Favelukis, M., Lavrenteva, O. M. & Nir, A. 2012 On the evolution and breakup of slender drops in an extensional flow. Phys. Fluids 24, 043101.Google Scholar
Favelukis, M. & Nir, A. 2001 Deformation of a slender bubble in a non-Newtonian liquid in an extensional flow. Chem. Engng Sci. 56, 4643–4648.Google Scholar
Hinch, E. J. 1980 The evolution of slender inviscid drops in an axisymmetric straining flow. J. Fluid Mech. 101, 545–553.CrossRefGoogle Scholar
Hinch, E. J. & Acrivos, A. 1979 Steady long slender droplets in two-dimensional straining motion. J. Fluid Mech. 91, 401–414.Google Scholar
Howell, P. D. & Siegel, M. 2004 The evolution of a slender non-axisymmetric drop in an extensional flow. J. Fluid Mech. 521, 155–180.CrossRefGoogle Scholar
Janssen, J. J. M., Boon, A. & Agterof, W. G. M. 1994 Droplet break-up in simple shear flow in the presence of emulsifiers. Colloids Surf. A 91, 141–148.Google Scholar
Khakhar, D. V. & Ottino, J. M. 1986 Deformation and breakup of slender drops in linear flows. J. Fluid Mech. 166, 265–285.CrossRefGoogle Scholar
Rallison, J. M. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid. Mech. 16, 45–66.Google Scholar
Renardy, Y. Y., Renardy, M. & Cristini, V. 2001 A new volume-of-fluid formulation for surfactants and simulations of drop deformation under shear at low viscosity ratio. Eur. J. Mech. (B/Fluids) 21, 49–59.Google Scholar
Sherwood, J. D. 1984 Tip streaming from slender drops in a nonlinear extensional flow. J. Fluid Mech. 144, 281–295.Google Scholar
Stone, H. A. 1994 Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid. Mech. 26, 65–102.CrossRefGoogle Scholar
Taylor, G. I. 1964 Conical free surfaces and fluid interfaces. In Proceedings of the 11th International Congress on Applied Mechanics, Munich, pp. 790–796. Springer.Google Scholar