Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marshall, Jonathan S.
2017.
Exact Formulae for the Effective Slip Length of a Symmetric Superhydrophobic Channel with Flat or Weakly Curved Menisci.
SIAM Journal on Applied Mathematics,
Vol. 77,
Issue. 5,
p.
1606.
Kaynan, Uri
and
Yariv, Ehud
2017.
Stokes resistance of a cylinder near a slippery wall.
Physical Review Fluids,
Vol. 2,
Issue. 10,
Schnitzer, Ory
and
Yariv, Ehud
2017.
Longitudinal pressure-driven flows between superhydrophobic grooved surfaces: Large effective slip in the narrow-channel limit.
Physical Review Fluids,
Vol. 2,
Issue. 7,
Yariv, Ehud
2017.
Velocity amplification in pressure-driven flows between superhydrophobic gratings of small solid fraction.
Soft Matter,
Vol. 13,
Issue. 37,
p.
6287.
Luca, Elena
Marshall, Jonathan
and
Karamanis, Georgios
2018.
Longitudinal shear flow over a bubble mattress with curved menisci: arbitrary protrusion angle and solid fraction.
IMA Journal of Applied Mathematics,
Kirk, Toby L.
2018.
Asymptotic formulae for flow in superhydrophobic channels with longitudinal ridges and protruding menisci.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
Schnitzer, Ory
and
Yariv, Ehud
2018.
Resistive-force theory for mesh-like superhydrophobic surfaces.
Physical Review Fluids,
Vol. 3,
Issue. 3,
Hodes, Marc
Kirk, Toby
and
Crowdy, Darren
2018.
Spreading and Contact Resistance Formulae Capturing Boundary Curvature and Contact Distribution Effects.
Journal of Heat Transfer,
Vol. 140,
Issue. 10,
Yariv, Ehud
and
Schnitzer, Ory
2018.
Pressure-driven plug flows between superhydrophobic surfaces of closely spaced circular bubbles.
Journal of Engineering Mathematics,
Vol. 111,
Issue. 1,
p.
15.
Yariv, Ehud
and
Crowdy, Darren
2020.
Longitudinal Thermocapillary Flow over a Dense Bubble Mattress.
SIAM Journal on Applied Mathematics,
Vol. 80,
Issue. 1,
p.
1.
Kirk, Toby L.
Karamanis, Georgios
Crowdy, Darren G.
and
Hodes, Marc
2020.
Thermocapillary stress and meniscus curvature effects on slip lengths in ridged microchannels.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Yariv, Ehud
2021.
Conductivity of a medium containing a dense array of perfectly conducting square cylinders.
Journal of Engineering Mathematics,
Vol. 127,
Issue. 1,
Yariv, Ehud
2023.
Effective slip length for longitudinal shear flow over partially invaded grooves: Small solid-fraction approximations.
Physical Review Fluids,
Vol. 8,
Issue. 1,
Yang, Haichang
Zeng, Binglin
Zhang, Xuehua
Xing, Yaowen
Gui, Xiahui
and
Cao, Yijun
2023.
Control of boundary slip by interfacial nanobubbles: A perspective from molecular dynamics simulations.
Physics of Fluids,
Vol. 35,
Issue. 3,
Yariv, Ehud
2023.
Highly singular slip length for longitudinal shear flow over a dense bubble mattress.
Journal of Fluid Mechanics,
Vol. 967,
Issue. ,
Yariv, E.
2023.
Effective slip length for transverse shear flow over partially invaded grooves.
Journal of Fluid Mechanics,
Vol. 957,
Issue. ,
Baier, Tobias
2023.
Influence of incompressible surfactant on drag in flow along an array of gas-filled grooves.
Physical Review Fluids,
Vol. 8,
Issue. 4,
Yariv, Ehud
2024.
Longitudinal Shear Flow over a Superhydrophobic Grating with Partially Invaded Grooves and Curved Menisci.
SIAM Journal on Applied Mathematics,
Vol. 84,
Issue. 3,
p.
1186.
Schnitzer, Ory
and
Ray, Prasun K.
2024.
Giant superhydrophobic slip of shear-thinning liquids.
Physical Review Fluids,
Vol. 9,
Issue. 11,
Miyoshi, Hiroyuki
Kirk, Toby L.
and
Hodes, Marc
2025.
On Spreading Resistance for an Isothermal Source on a Compound Flux Channel.
ASME Journal of Heat and Mass Transfer,
Vol. 147,
Issue. 9,
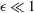 $\unicode[STIX]{x1D716}\ll 1$ . Using scaling arguments and utilising an ideal-flow analogy we elucidate the singularity of the slip length as
$\unicode[STIX]{x1D716}\ll 1$ . Using scaling arguments and utilising an ideal-flow analogy we elucidate the singularity of the slip length as 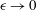 $\unicode[STIX]{x1D716}\rightarrow 0$ : relative to the periodicity it scales as
$\unicode[STIX]{x1D716}\rightarrow 0$ : relative to the periodicity it scales as 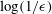 $\log (1/\unicode[STIX]{x1D716})$ for protrusion angles
$\log (1/\unicode[STIX]{x1D716})$ for protrusion angles 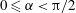 $0\leqslant \unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$ and as
$0\leqslant \unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$ and as 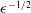 $\unicode[STIX]{x1D716}^{-1/2}$ for
$\unicode[STIX]{x1D716}^{-1/2}$ for 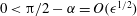 $0<\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC}=O(\unicode[STIX]{x1D716}^{1/2})$ . We continue with a detailed asymptotic analysis using the method of matched asymptotic expansions, where ‘inner’ solutions valid close to the solid segments are matched with ‘outer’ solutions valid on the scale of the periodicity, where the bubbles protruding from the solid grooves appear to touch. The analysis yields asymptotic expansions for the effective slip length in each of the protrusion-angle regimes. These expansions overlap for intermediate protrusion angles, which allows us to form a uniformly valid approximation for arbitrary protrusion angles
$0<\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC}=O(\unicode[STIX]{x1D716}^{1/2})$ . We continue with a detailed asymptotic analysis using the method of matched asymptotic expansions, where ‘inner’ solutions valid close to the solid segments are matched with ‘outer’ solutions valid on the scale of the periodicity, where the bubbles protruding from the solid grooves appear to touch. The analysis yields asymptotic expansions for the effective slip length in each of the protrusion-angle regimes. These expansions overlap for intermediate protrusion angles, which allows us to form a uniformly valid approximation for arbitrary protrusion angles 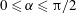 $0\leqslant \unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/2$ . We thereby explicitly describe the transition with increasing protrusion angle from a logarithmic to an algebraic small-solid-fraction slip-length singularity.
$0\leqslant \unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/2$ . We thereby explicitly describe the transition with increasing protrusion angle from a logarithmic to an algebraic small-solid-fraction slip-length singularity.

