1 Introduction
Falling liquid films have been a topic of fundamental and applied research for several decades since the pioneering experiments by Kapitza (Reference Kapitza1948) and Kapitza & Kapitza (Reference Kapitza and Kapitza1949). A falling liquid film is a convectively unstable open-flow hydrodynamic system with a rich variety of spatiotemporal structures and a sequence of wave instabilities and transitions that are generic to a large class of hydrodynamic and other nonlinear systems. Despite their apparent complexity one can still identify robust coherent structures, i.e. solitary waves, in what appears to be a randomly disturbed surface. These structures interact continuously with each other as quasiparticles. Hence, a falling liquid film can serve as a canonical reference system for the study of spatiotemporal chaos and weak/dissipative turbulence. In addition, falling liquid films are typically associated with low flow rates, low pressure drops, small thermal resistances and large contact areas per unit volume. Not surprisingly, they play a central role in a wide spectrum of engineering applications. Prominent examples of applications involving falling liquid films are evaporators–condensers, heat exchangers, chemical reactor columns and cooling devices. Falling liquid films are also exploited in saltwater desalination plants, in the food processing industry as well as in coating processes. Furthermore, falling liquid films are found in problems related to earth science and geophysics, for instance underwater gravity currents, lava flows and the propagation of bores in rivers. Therefore, an accurate understanding of the hydrodynamics of falling liquid films is crucial in the design and optimisation of processes and devices that exploit these flows. The present study focuses on the hydrodynamic mechanisms that govern solitary waves on inertia-dominated falling films and, in particular, on flow features that have been shown to improve the heat and mass transport characteristics of the films.
1.1 Theory and physical aspects
A falling liquid film is unstable to long-wave perturbations above a critical Reynolds number (Yih Reference Yih1963) due to an instability mechanism that is mainly driven by shear stresses acting at the interface (Hinch Reference Hinch1984; Kelly et al. Reference Kelly, Goussis, Lin and Hsu1989; Smith Reference Smith1990). In general, inertia and the streamwise component of gravity destabilise the flow, whereas surface tension and the cross-stream component of gravity have a stabilising effect. A natural source of perturbations to a falling film flow is white noise at the inlet, whereby the resulting instability selects the fastest growing mode of the system followed by a secondary modulation instability that converts the primary wave field into solitary waves (Liu, Paul & Gollub Reference Liu, Paul and Gollub1993; Chang Reference Chang1994; Kalliadasis et al. Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012). Liu & Gollub (Reference Liu and Gollub1994), however, reported regular waves by imposing a monochromatic perturbation at the inlet in their experimental arrangement. In this case, the instability synchronises with the inlet forcing frequency (Liu et al. Reference Liu, Paul and Gollub1993; Chang Reference Chang1994), provided that the forcing amplitude is sufficiently large.
At low forcing frequencies, the long-wave instability develops into fast-moving solitary waves that consist of a primary wave hump preceded by capillary ripples at the front. These waves are predominantly two-dimensional (2D) structures (Leontidis et al.
Reference Leontidis, Vatteville, Vlachogiannis, Andritsos and Bontozoglou2010), and in the inertia-dominated regime (typically for Reynolds numbers,
$Re\simeq 20{-}200$
) the velocity profile can deviate strongly from its originally parabolic shape (Malamataris, Vlachogiannis & Bontozoglou Reference Malamataris, Vlachogiannis and Bontozoglou2002; Scheid, Ruyer-Quil & Manneville Reference Scheid, Ruyer-Quil and Manneville2006). In addition, if the inertia of the liquid film is sufficiently high, the maximum velocity of the fluid exceeds the wave speed of the solitary waves, leading to a recirculation zone in the moving frame (Maron, Brauner & Hewitt Reference Maron, Brauner and Hewitt1989). This zone, which appears in the main hump of the solitary waves, can considerably impact the heat and mass transport in the film due to the enhanced mixing (Roberts & Chang Reference Roberts and Chang2000; Albert, Marschall & Bothe Reference Albert, Marschall and Bothe2014). Previous studies have found that the wave frequency, the inclination angle of the substrate, as well as viscous dispersion and capillary effects have a significant influence on the extent of the recirculation zone (Miyara Reference Miyara2000; Rohlfs & Scheid Reference Rohlfs and Scheid2015).
The number of capillary ripples preceding a solitary hump increases with decreasing forcing frequency, increasing Reynolds number and decreasing viscous dispersion (Nosoko et al. Reference Nosoko, Yoshimura, Nagata and Oyakawa1996; Pradas, Tseluiko & Kalliadasis Reference Pradas, Tseluiko and Kalliadasis2011), in order for surface tension to balance inertia. Capillary ripples propagate at the same speed as the main hump of the solitary wave (Dietze Reference Dietze2016), since they are continuously compressed by the main hump. As a result, faster capillary ripples have a larger amplitude (Dietze Reference Dietze2016), in contrast to freely oscillating capillary waves which exhibit a smaller phase velocity for increasing initial wave amplitude (Denner, Pare & Zaleski Reference Denner, Pare and Zaleski2017a ). Due to the high interface curvature of the capillary ripples, pressure gradients in the streamwise direction are significant and may lead to flow separation and local reversal of the flow direction in the laboratory frame of reference. This phenomenon was first noted by Portalski (Reference Portalski1964) and Massot, Irani & Lightfoot (Reference Massot, Irani and Lightfoot1966), and was later investigated in more detail in terms of the underlying mechanisms (Dietze, Leefken & Kneer Reference Dietze, Leefken and Kneer2008; Dietze, Al-Sibai & Kneer Reference Dietze, Al-Sibai and Kneer2009) and the influence of inertia, wave frequency and inclination angle (Malamataris & Balakotaiah Reference Malamataris and Balakotaiah2008; Chakraborty et al. Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014; Rohlfs & Scheid Reference Rohlfs and Scheid2015). Numerical simulations conducted by Kunugi & Kino (Reference Kunugi and Kino2005) demonstrated a considerable enhancement of the heat and mass transport characteristics of the film as a result of flow reversal.
1.2 Experimental and numerical methods
From an experimental point of view, a range of optical (typically laser-based) methods have been developed for the investigation of the instantaneous motion and spatial extent of unsteady interfacial flows and, specifically, liquid film flows (Lel et al.
Reference Lel, Al-Sibai, Leefken and Renz2005; Schlagen et al.
Reference Schlagen, Modigell, Dietze and Kneer2006). Fluorescence intensity-based measurements of the instantaneous and local film height have been conducted, for example, in laminar falling films (Liu & Gollub Reference Liu and Gollub1993; Liu et al.
Reference Liu, Paul and Gollub1993), in annular gas–liquid flows (Alekseenko et al.
Reference Alekseenko, Antipin, Cherdantsev, Kharlamov and Markovich2009, Reference Alekseenko, Cherdantsev, Cherdantsev, Isaenkov, Kharlamov and Markovich2012) and in gas-sheared liquid flows in a horizontal rectangular duct (Cherdantsev, Hann & Azzopardi Reference Cherdantsev, Hann and Azzopardi2014). Liu and co-workers (Liu & Gollub Reference Liu and Gollub1993; Liu et al.
Reference Liu, Paul and Gollub1993) determined the critical
$Re$
for the onset of wave formation as a function of the inclination angle, and a phase boundary which separates the saturated, finite-amplitude wave regime from the multipeaked solitary wave regime was identified. In the work of Alekseenko et al. (Reference Alekseenko, Antipin, Cherdantsev, Kharlamov and Markovich2009, Reference Alekseenko, Cherdantsev, Cherdantsev, Isaenkov, Kharlamov and Markovich2012) and Cherdantsev et al. (Reference Cherdantsev, Hann and Azzopardi2014), 2D and three-dimensional (3D) film-thickness measurements were used to scrutinise the topology of large-amplitude disturbance waves as a function of
$Re$
, and to link the generation of ripples forming atop these waves to the mechanisms of liquid entrainment. Markides and co-workers (Zadrazil, Matar & Markides Reference Zadrazil, Matar and Markides2014a
; Charogiannis, An & Markides Reference Charogiannis, An and Markides2015) used planar laser-induced fluorescence imaging (PLIF) instead, in order to investigate the coupling between the film-thickness and velocity-field variations over a 2D domain. In Mathie, Nakamura & Markides (Reference Mathie, Nakamura and Markides2013) and Markides, Mathie & Charogiannis (Reference Markides, Mathie and Charogiannis2015), the same technique was employed alongside infrared thermography (IR), thus allowing for interface-temperature measurements to be retrieved simultaneously with film-thickness measurements. Based on this approach, the authors reported significant heat transport enhancements depending on film topology.
Optical velocimetry techniques can broadly be categorised depending on whether a molecular-tagging or particle-seeding approach is adopted. The photochromic dye activation (PDA) technique stands as a prime example of the former, allowing for direct velocity-profile measurements via the generation of thin fluorescing traces arranged perpendicular to the direction of the flow (Karimi & Kawaji Reference Karimi and Kawaji2000; Moran, Inumaru & Kawaji Reference Moran, Inumaru and Kawaji2002). Particle-image velocimetry (PIV) and particle tracking velocimetry (PTV), instead, allow for 2D as well as 3D velocity-field characterisation by tracking the motion of seeded particle groups (PIV) or individual particles (PTV). Examples of the use of micro-PIV include the study of laminar, vertically falling films (Adomeit & Renz Reference Adomeit and Renz2000) and the capillary-wave region (Dietze et al. Reference Dietze, Leefken and Kneer2008), while PIV/PTV has been used, for example, in the study of downward co-current gas–liquid annular flows (Zadrazil, Matar & Markides Reference Zadrazil, Matar and Markides2014b ), where the presence of multiple recirculation zones within the disturbance waves was revealed.
In terms of modelling and computational methodologies, a substantial number of studies have focused on low-dimensional (LD) formulations, which simplify the governing equations and associated wall and free-surface boundary conditions considerably. Using the long-wave expansion, a hierarchy of model equations has been obtained, starting from the so-called Benney equation (Benney Reference Benney1966) whose region of validity is restricted to near-critical conditions (Kalliadasis et al.
Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012), to integral-boundary-layer equations which are valid away from criticality and describe the evolution of both the film height
$h$
and the local flow rate
$q$
(Shkadov Reference Shkadov1967) (see also the work by Scheid et al. (Reference Scheid, Ruyer-Quil and Manneville2006), where different LD models are compared to each other). Numerical modelling has also received considerable attention, with direct numerical simulation (DNS) finding increasing application in the study of falling liquid films. The work of Ramaswamy, Chippada & Joo (Reference Ramaswamy, Chippada and Joo1996) was the first DNS study to conduct a detailed investigation of this problem, focusing on the stability of falling films as well as on the development and interaction of interfacial instabilities. Subsequently, Malamataris et al. (Reference Malamataris, Vlachogiannis and Bontozoglou2002) showed that the velocity profile of the liquid film is strongly non-parabolic in solitary waves, whereas studies of Gao, Morley & Dhir (Reference Gao, Morley and Dhir2003) and Nosoko & Miyara (Reference Nosoko and Miyara2004) investigated the dynamics of periodically perturbed falling films at different forcing frequencies and Reynolds numbers. A common assumption made in the majority of computational studies is a periodic computational domain in which the film thickness is conserved, hence increasing the flow rate at the onset of interface waves (Ramaswamy et al.
Reference Ramaswamy, Chippada and Joo1996; Gao et al.
Reference Gao, Morley and Dhir2003) and imposing a particular wavelength on the instabilities (Kalliadasis et al.
Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012). In reality, however, the system is not closed but open and, therefore, it is not the mean film thickness but the mean flow rate that is conserved, resulting in a decrease of the average film thickness for wavy film flows (Chang, Demekhin & Kalaidin Reference Chang, Demekhin and Kalaidin1995; Gao et al.
Reference Gao, Morley and Dhir2003). Numerical studies using periodic domains are, hence, limited in their ability to accurately predict spatiotemporally evolving interface instabilities.
1.3 Objectives
Despite the significant number of studies focusing on the hydrodynamics of solitary waves on falling liquid films, most of which have been conducted in the region of small-to-moderate Reynolds numbers (
$\mathit{Re}\lesssim 20$
), a number of open questions regarding the hydrodynamics of inertia-dominated solitary waves still remain. Previous DNS studies (Chakraborty et al.
Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014; Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016) have reported results in which the wave height stagnates, meaning it stays approximately constant, or reduces when increasing the Reynolds number above a critical value. Considering that the wavelength of solitary waves increases for larger Reynolds numbers (Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), a yet unidentified mechanism must be responsible for the saturation (stagnation or reduction) of the height of solitary waves. Similarly, with respect to the flow reversal observed underneath the trough preceding the solitary wave, the hydrodynamic mechanisms responsible for the upper limit in Reynolds number above which no flow reversal was observed in simulations of Chakraborty et al. (Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014) have yet to be explained. It is also worth noting that none of the previous studies included a detailed and systematic comparison between experimental measurements and numerical results using LD models or DNS. If such a comparison confirms good agreement, a concurrent application of these methods may provide more detailed insight into the complex hydrodynamics of solitary waves.
Aiming to provide answers to these open questions, we adopt a synergistic approach with a combination of experiments, DNS as well as LD modelling. A direct comparison of experimental and numerical results is instrumental in assessing the predictive quality of the available computational methods and in analysing the flow field and wave characteristics in detail. We find that experimental measurements and DNS results agree very well, in particular with respect to film height and flow velocity at the interface, while the applied LD model is favourably compared with both of them. Of particular interest in our study is the flow field within the falling liquid films and its influence on the dynamics of solitary waves and capillary ripples, in order to elucidate the mechanisms stabilising the wave height and influencing the flow separation and reversal at large Reynolds numbers. The presented experimental and numerical results can also serve as a benchmark for future studies of the hydrodynamics of falling liquid films.
In § 2 the characterisation of falling liquid films and the associated solitary waves is discussed. In § 3 we introduce the experimental and numerical methods we adopt and detail the case studies we undertake. The results are presented and discussed in § 4 and conclusions are offered in § 5.
2 Characterisation of falling liquid films
Consider a film flowing down a planar inclined plane forming an angle
$\unicode[STIX]{x1D6FD}$
with the horizontal direction, as shown in figure 1. There exists a spatially uniform solution, often referred to as the Nusselt flat-film solution (Nusselt Reference Nusselt1916), with film height
$$\begin{eqnarray}h_{\mathit{N}}=\sqrt[3]{\frac{3\unicode[STIX]{x1D707}_{\mathit{l}}q_{N}}{\unicode[STIX]{x1D70C}_{\mathit{l}}g\sin \unicode[STIX]{x1D6FD}}}\end{eqnarray}$$
and average film velocity
$$\begin{eqnarray}u_{\mathit{N}}=\frac{\unicode[STIX]{x1D70C}_{\mathit{l}}g\sin \unicode[STIX]{x1D6FD}h_{\mathit{N}}^{2}}{3\unicode[STIX]{x1D707}_{\mathit{l}}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}_{\mathit{l}}$
and
$\unicode[STIX]{x1D70C}_{\mathit{l}}$
are the dynamic viscosity and the density of the liquid film, respectively,
$q_{N}=u_{N}h_{N}$
is the flow rate per unit span and
$g$
is the gravitational acceleration. Based on this idealised solution, various characteristic scalings can be formulated.
Figure 1. Sketch of the profile geometry for a liquid film on a substrate with inclination angle
$\unicode[STIX]{x1D6FD}$
to the horizontal.
$h(x,t)$
is the local film thickness with respect to a Cartesian coordinate system
$(x,y)$
, with
$x$
the streamwise coordinate and
$y$
the outward-pointing coordinate normal to the substrate.
2.1 Nusselt scaling
Making use of the representative pressure scales of the three major hydrodynamic mechanisms acting on the falling film (inertia, viscous stresses and surface tension) several dimensionless parameters can be defined. The Reynolds number
$$\begin{eqnarray}\mathit{Re}=\frac{\unicode[STIX]{x1D70C}_{\mathit{l}}h_{\mathit{N}}u_{\mathit{N}}}{\unicode[STIX]{x1D707}_{\mathit{l}}}\end{eqnarray}$$
expresses the relative importance of inertia over viscous effects, the Weber number
$$\begin{eqnarray}\mathit{We}=\frac{\unicode[STIX]{x1D70C}_{\mathit{l}}h_{\mathit{N}}u_{\mathit{N}}^{2}}{\unicode[STIX]{x1D70E}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D70E}$
is the surface tension, represents the relative importance of inertia to surface tension, and the capillary number,
$$\begin{eqnarray}\mathit{Ca}=\frac{\unicode[STIX]{x1D707}_{\mathit{l}}u_{\mathit{N}}}{\unicode[STIX]{x1D70E}},\end{eqnarray}$$
a measure of the relative importance of viscous stresses and surface tension. The Reynolds number
$\mathit{Re}$
can also be regarded as the dimensionless flow rate. These non-dimensional numbers are related to each other by
$\mathit{We}=\mathit{Re}\,\mathit{Ca}$
and are often referred to as Nusselt scaling in the context of falling liquid films, because they are based directly on the Nusselt flat-film solution. Numerical results presented by Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016) suggest that the capillary number is not suitable to characterise inertia-dominated solitary waves.
Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016) recently proposed an ‘inertia-corrected scaling’ for the characterisation of solitary waves on falling liquid films based on the driving Nusselt velocity
$u_{\mathit{N}}^{\ast }=u_{\mathit{N}}\sin \unicode[STIX]{x1D6FD}$
. Using this velocity scale, the Reynolds and Weber numbers are redefined as
$\mathit{Re}^{\ast }=\mathit{Re}\sin \unicode[STIX]{x1D6FD}$
and
$\mathit{We}^{\ast }=\mathit{We}(\sin \unicode[STIX]{x1D6FD})^{2}$
, respectively, which was shown to lead to a self-similar characterisation of the shape and dispersion of solitary waves on falling water films for a given inclination angle of the substrate and forcing frequency.
Unlike the dimensionless numbers above, which depend on the flow rate, the Kapitza number
$$\begin{eqnarray}\mathit{Ka}=\frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70C}_{\mathit{l}}\unicode[STIX]{x1D708}_{\mathit{l}}^{4/3}(g\sin \unicode[STIX]{x1D6FD})^{1/3}}=\frac{\mathit{Re}^{2/3}}{3^{1/3}\mathit{Ca}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D708}_{l}=\unicode[STIX]{x1D707}_{l}/\unicode[STIX]{x1D70C}_{l}$
is the liquid kinematic viscosity, depends only on the properties of the liquid and inclination angle
$\unicode[STIX]{x1D6FD}$
. Hence, for a fixed liquid and
$\unicode[STIX]{x1D6FD}$
, the Kapitza number is fixed and the only free parameter is the Reynolds number.
2.2 Shkadov scaling
Following the scaling introduced by Shkadov (Reference Shkadov1977), a reduced Reynolds number
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}=3\mathit{Re}\sqrt[3]{3\mathit{Ca}}\end{eqnarray}$$
and the viscous dispersion number
$$\begin{eqnarray}\unicode[STIX]{x1D702}=\sqrt[3]{9\mathit{Ca}^{2}}\end{eqnarray}$$
can be obtained. This reduced Reynolds number
$\unicode[STIX]{x1D6FF}$
compares inertia and viscous effects at the length scale imposed by surface tension and gravity. On the other hand, the viscous dispersion number
$\unicode[STIX]{x1D702}$
appears along with every second-order streamwise viscous term in the momentum equation and has a dispersive effect on the speed of linear waves (Pradas et al.
Reference Pradas, Tseluiko and Kalliadasis2011; Kalliadasis et al.
Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012). The Shkadov scaling is particularly useful for the characterisation of LD models, as further discussed with respect to the applied LD model in § 3.3.
Based on the reduced Reynolds number
$\unicode[STIX]{x1D6FF}$
, Ooshida (Reference Ooshida1999) identified two regimes: the drag-gravity regime for
$\unicode[STIX]{x1D6FF}\lesssim 1$
and the drag-inertia regime for
$\unicode[STIX]{x1D6FF}\gtrsim 1$
. In the drag-gravity regime, the flow is similar to that of the Nusselt flat-film solution, with both inertia and surface tension playing effectively a perturbative role (Kalliadasis et al.
Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012). In the drag-inertia regime on the other hand, inertia and surface tension are no longer corrections to the Nusselt flow, the cross-stream velocity component becomes significant and the velocity profile of the film flow can become strongly non-parabolic (Malamataris et al.
Reference Malamataris, Vlachogiannis and Bontozoglou2002). Recent studies (Chakraborty et al.
Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014; Rohlfs & Scheid Reference Rohlfs and Scheid2015) found the transition between the drag-gravity and drag-inertia regimes to occur at
$1\lesssim \unicode[STIX]{x1D6FF}\lesssim 6$
. Additional effects – for example, shear-thinning and non-Newtonian behaviour – can lead to complex behaviour in the vicinity of this transition (such as hysteresis) (Pradas et al.
Reference Pradas, Tseluiko, Ruyer-Quil and Kalliadasis2014).
3 Methods
3.1 Experimental methodology
The experimental apparatus and methodologies developed to generate the film thickness and velocity data have been described extensively in our previous publications (Charogiannis et al.
Reference Charogiannis, An and Markides2015, Reference Charogiannis, Denner, van Wachem, Kalliadasis and Markides2017), and therefore only a summary is presented here for the sake of clarity and completeness. A schematic of the experimental arrangement, itself an evolution of a previously developed set-up (Mathie et al.
Reference Mathie, Nakamura and Markides2013; Markides et al.
Reference Markides, Mathie and Charogiannis2015), is depicted in figure 2. The apparatus consists of a main test section over which film flows develop, and a closed loop via which the liquid circulates. Prior to entering a flow-preparation distribution box, the flow is split into a steady supply
$Q$
and a pulsating supply
$Q^{\prime }$
. The latter is generated by an oscillator valve that allows accurate control of the forcing frequency and amplitude to be achieved, selectively triggering the rapid growth of fully developed wave regimes within the confines of our test section. The instantaneous flow rate into the distribution box is calculated from the output signal of an ultrasonic flowmeter. The role of the distribution box is to create a well-characterised uniform flow with low noise levels, and to introduce this over the test section with uniform thickness.
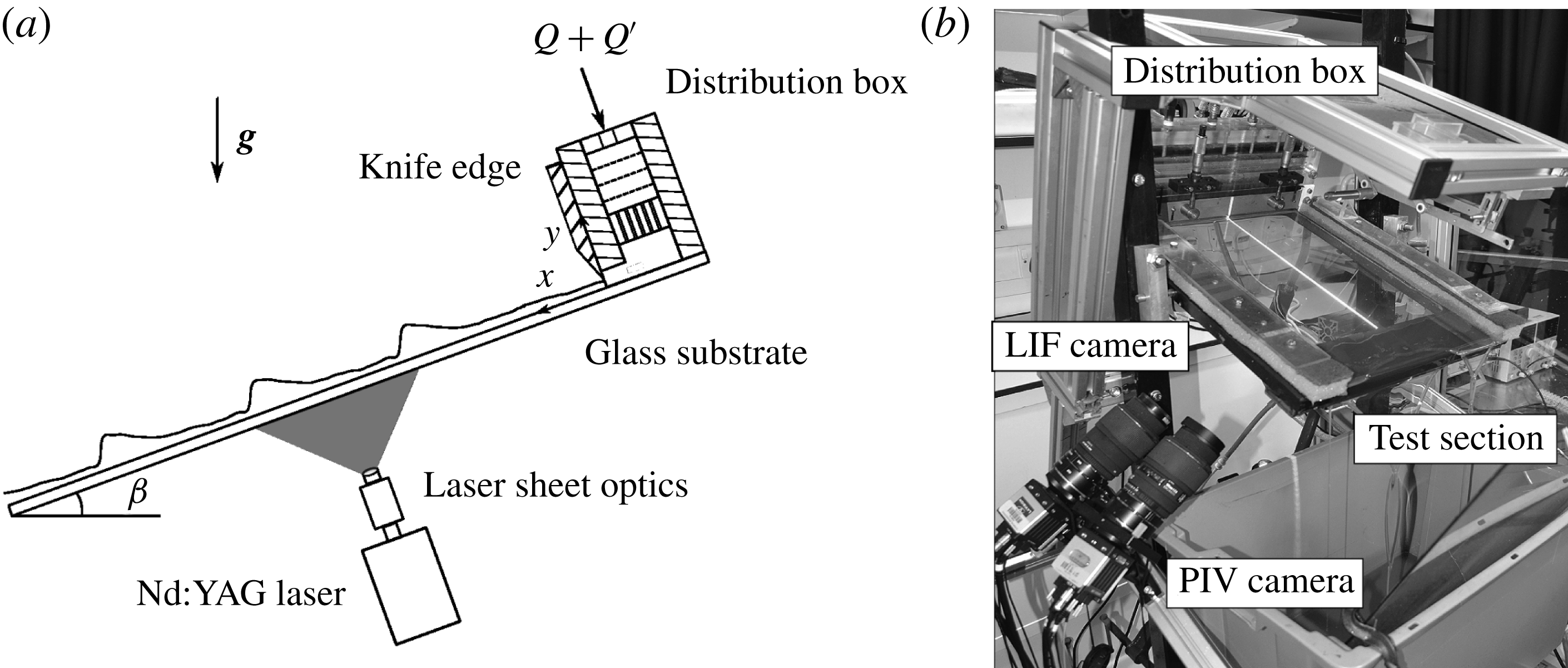
Figure 2. (a) Schematic of the test section and part of the flow loop. (b) Test section arrangement showing the position of the cameras and illuminated region of the film (Charogiannis et al. Reference Charogiannis, An and Markides2015, Reference Charogiannis, Denner, van Wachem, Kalliadasis and Markides2017).
3.1.1 Test section and imaging arrangement
The test section comprises a thin soda-lime glass plate with 0.7 mm thickness, mounted on an aluminium support frame and inclined at
$20^{\circ }$
to the horizontal. The Reynolds number can be evaluated at the flow inlet using the mean flow-rate measurement per unit width of the channel
$Q$
, as
$$\begin{eqnarray}\mathit{Re}_{box}=\frac{DU_{box}}{\unicode[STIX]{x1D708}}=\frac{Q}{\unicode[STIX]{x1D708}},\end{eqnarray}$$
where
$U_{box}$
is the bulk velocity inside the box and
$D$
is the channel depth. A frequency-doubled Nd:YAG laser (532 nm) is used to illuminate the flow, which is seeded with Rhodamine B dye for PLIF and glass-hollow-sphere particles for PIV, at a sampling rate of
$100~\text{s}^{-1}$
. Sheet optics are employed in forming a thin (approximately 0.1 mm) laser sheet extending along the (streamwise) length of the substrate, while a pair of LaVision HS 500 CMOS cameras equipped with Sigma 105 mm f/2.8 Macro lenses are employed to achieve the desired magnification (between
$28.0~\unicode[STIX]{x03BC}\text{m}$
and
$29.7~\unicode[STIX]{x03BC}\text{m}$
per pixel depending on
$\mathit{Ka}$
). Excitation of the dye-doped liquid and imaging of the emitted fluorescence is performed from underneath (unwetted side), in order to avoid spatially and temporally non-uniform beam stirring and lensing in the first instance, and to limit image distortions in the latter. The imaging planes of the two cameras are mapped using a calibration graticule target immersed inside the liquid solution. Optical distortion corrections are performed using the same arrangement, and a pinhole model available in LaVision DaVis.
3.1.2 PLIF/PTV data acquisition and processing
A sample PLIF frame after correction for perspective distortion is depicted in figure 3(a). Near the solid–liquid interface, reflections from the substrate blur the PLIF signal locally, while the fluorescence emitted by the illuminated liquid volume is reflected about the liquid–gas interface and back to the camera. The location of the solid–liquid interface is obtained using an edge-detection algorithm, while for the gas–liquid interface, intercepts between linear fits to maximum signal gradients and reflection intensity profiles are employed as estimates of the liquid boundaries. The processed profiles are then used to mask out the reflection regions and to produce binarised images (see figure 3 b), where a signal intensity of unity corresponds to the film domain and a signal intensity of zero is ascribed to the rest of the image.
Figure 3. (a) PLIF image from a flow with
$\mathit{Re}=62$
,
$\mathit{Ka}=350$
and
$f=10~\text{s}^{-1}$
, following corrections for refractive-index and perspective distortions, and (b) binarised PLIF image after removal of out-of-plane reflections. (c) Particle image from a flow with
$\mathit{Re}=24$
,
$\mathit{Ka}=85$
and
$f=10~\text{s}^{-1}$
after corrections for refractive-index and perspective distortions, and (d) masked-particle image using its processed PLIF counterpart.
The binarised images are used to mask out reflections from the glass surface underneath the liquid domain and about the gas–liquid interface in the raw particle images (see figure 3 c,d). A four-pass cross-correlation algorithm is implemented on the masked-particle-image sequences in order to generate 2D velocity-vector maps (PIV calculation). Following this step, individual particles are tracked (PTV calculation) by employment of the obtained PIV results as reference estimators of the velocity field. There are a number of reasons for employing PTV rather than PIV in this study. To begin with, PTV offers an eight-fold increase in the spatial resolution of the velocity measurement based on the selected velocity-vector calculation settings (which are determined based on the optical set-up, the size of imaged region of the flow and the employed particles). A second reason is that PIV suffers from large bias errors in the presence of strong velocity gradients, as the motion of particle groups is averaged within the PIV interrogation window. Along a smooth film region and near the gas–liquid interface this effect is of little consequence, and PTV and PIV produce similar results. Near the wall, however, as well as between the wave crests and troughs, and along the capillary-wave regions, where the velocity varies strongly over a limited spatial domain, PIV falls short of providing credible quantitative results. It should finally be noted that the presence of particle-image reflections within the masked liquid domain constitutes a commonly encountered error source affecting the PTV velocity data (Kaehler, Scholz & Ortmanns Reference Kaehler, Scholz and Ortmanns2006; Kaehler, Scharnowski & Cierpka Reference Kaehler, Scharnowski and Cierpka2012). In our experiments, a spatial extent corresponding to only approximately 5 %–7 % of the examined films is strongly affected by such artefacts, and consequently, the impact on bulk velocity measurements is minimal.
For a detailed examination of the velocity distributions underneath the waves, the practice of averaging PTV maps corresponding to the same spatial region is adopted. The procedure is initialised by selecting a reference film-thickness profile pertaining to the desired topology, and cross-correlating it with all thickness traces from the same data set. Signal pairs satisfying a maximum displacement condition are then repositioned and averaged (a typical result is shown in figure 4 a). The same translation values are used to rearrange and average out the corresponding instantaneous PTV velocity maps, producing averaged velocity fields such as the one displayed in figure 4(b).
Figure 4. (a) Reference and average-wave profiles for a film with
$\mathit{Re}=26.9$
,
$\mathit{Ka}=85$
and a
$10~\text{s}^{-1}$
forcing frequency. (b) Average PTV-derived velocity field corresponding to the average film-thickness profile in (a).
3.1.3 Validation
Independent experiments are conducted in order to assess the validity and accuracy of the combined optical methodology. Film thicknesses from flat films (
$\mathit{Ka}=14$
) are compared to predictions from the Nusselt flat-film solution and direct micrometre-stage measurements. In both cases the mean relative-deviation amounts to below 1 %. The same uncertainty value is believed to apply to wave-locked average measurements of mean film thickness; however, thinner films ensue in that case, and consequently a worst-case uncertainty of 2 % is a more representative estimate. An estimate of the film-thickness measurement noise is obtained by calculating standard deviations over a wide range of flat-film datasets. This amounts to
${<}30~\unicode[STIX]{x03BC}\text{m}$
, and therefore, a mean relative error of 2.5 % is quoted for the instantaneous film-thickness measurements.
Relative deviations are also calculated between PTV-derived interfacial and bulk velocities, and corresponding analytical results of the Nusselt flat-film solution, with average relative deviations corresponding to 3.2 % for both velocities. Standard deviations of local velocity in flat films (conservative estimates of PTV measurement noise) are observed to decrease with increasing distance from the wall; at the gas–liquid interface, they typically amount to less than 1 % of the local mean value, while halfway across the film thickness they amount to approximately 5 %–6 % of the mean value.
3.2 DNS methodology
The applied DNS methodology is based on a general-purpose finite-volume framework for interfacial flows (Denner & van Wachem Reference Denner and van Wachem2014a ), which resolves the dynamics of the full two-phase system, i.e. the liquid film, the gas–liquid interface and the gas phase. The flow, which is assumed to be incompressible and isothermal, is governed by the momentum equations
$$\begin{eqnarray}\unicode[STIX]{x1D70C}\left(\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{u})\right)=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D707}[\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}}]+\unicode[STIX]{x1D70C}\boldsymbol{g}+\boldsymbol{f}_{\unicode[STIX]{x1D70E}}\end{eqnarray}$$
and the continuity equation
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\end{eqnarray}$$
where
$t$
represents time,
$\boldsymbol{u}$
is the velocity,
$p$
is the pressure,
$\unicode[STIX]{x1D70C}$
is the density,
$\unicode[STIX]{x1D707}$
is the dynamic viscosity,
$\boldsymbol{g}$
is the gravitational acceleration and
$\boldsymbol{f}_{\unicode[STIX]{x1D70E}}$
represents the contribution of the surface tension.
3.2.1 Numerical framework
The primitive variables are obtained using a coupled, implicit finite-volume framework with collocated variable arrangement (Denner & van Wachem Reference Denner and van Wachem2014a ). The momentum equations (3.2) are discretised using a second-order backward Euler scheme for the transient term, while the convection, diffusion and pressure terms are discretised using central differencing. The continuity equation (3.3) is discretised using a balanced-force implementation of the momentum-weighted interpolation method, as proposed by Denner & van Wachem (Reference Denner and van Wachem2014a ), which couples pressure and velocity.
The volume-of-fluid (VOF) method (Hirt & Nichols Reference Hirt and Nichols1981) is adopted to capture the gas–liquid interface. In the VOF method the local volume fraction in each cell is represented by the colour function
$\unicode[STIX]{x1D6FE}$
, defined as
$\unicode[STIX]{x1D6FE}=0$
in fluid
$a$
and
$\unicode[STIX]{x1D6FE}=1$
in fluid
$b$
. Hence, the interface is located in mesh cells with a colour function value of
$0<\unicode[STIX]{x1D6FE}<1$
. The colour function is advected by the linear advection equation
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x2202}t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FE}=0,\end{eqnarray}$$
which is discretised using a compressive VOF methodology (Denner & van Wachem Reference Denner and van Wachem2014b
). Assuming surface tension is a volume force acting in the interface region, the surface force per unit volume is described by the continuum surface force (CSF) model (Brackbill, Kothe & Zemach Reference Brackbill, Kothe and Zemach1992) as
$\boldsymbol{f}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D705}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FE}$
, where
$\unicode[STIX]{x1D705}$
represents the interface curvature. The artificial viscosity model for interfacial flows of Denner et al. (Reference Denner, Evrard, Serfaty and van Wachem2017b
) is also applied to mitigate the impact of parasitic and spurious flow features on the numerical solution.
3.2.2 Simulation set-up
The applied two-dimensional computational domain, illustrated in figure 5, has the dimensions
$L_{x}\times L_{y}$
, where
$L_{y}=4h_{\mathit{N}}$
and the domain length
$L_{x}=0.256~\text{m}+50h_{\mathit{N}}$
is chosen to allow a direct comparison with the corresponding experimental results at the experimental measurement point
$x_{\mathit{m}}=0.256~\text{m}$
downstream from the inlet. The additional domain length of
$50h_{\mathit{N}}$
is taken to be sufficiently long so as to ensure that the outlet of the computational domain does not affect the flow field and interface instabilities in the measurement region. The computational domain is represented by an equidistant Cartesian mesh with a resolution of 10 cells per film height
$h_{\mathit{N}}$
. The time step
$\unicode[STIX]{x0394}t$
satisfies a Courant number of
$\mathit{Co}=|\boldsymbol{u}|\unicode[STIX]{x0394}t/\unicode[STIX]{x0394}x\leqslant 0.25$
as well as the capillary time-step constraint derived by Denner & van Wachem (Reference Denner and van Wachem2015). The properties of the liquid film are directly taken from the experimental measurements (see § 3.4) and the gas phase is assumed to be air with density
$\unicode[STIX]{x1D70C}_{\mathit{g}}=1.205~\text{kg}~\text{m}^{-3}$
and viscosity
$\unicode[STIX]{x1D707}_{\mathit{g}}=1.82\times 10^{-5}~\text{Pa}~\text{s}$
.
Figure 5. Schematic illustration of the numerical domain with dimensions
$(L_{x}\times L_{y})$
. The liquid film with height
$h(x,t)$
flows from the left to the right on an inclined substrate.
At the bottom (liquid-side) wall a no-slip condition is enforced and at the top (gas-side) boundary a free-slip wall is applied. A monochromatic forcing is imposed at the domain inlet by periodically changing the mass flow at a given frequency
$f$
and amplitude
$A$
from the mean. A semiparabolic velocity profile is prescribed for the liquid phase at the inlet
$$\begin{eqnarray}u(x=0,0\leqslant y\leqslant h_{\mathit{N}})=\frac{3}{2}[1+A\sin (2\unicode[STIX]{x03C0}ft)]\left(2\frac{y}{h_{\mathit{N}}}-\frac{y^{2}}{h_{\mathit{N}}^{2}}\right)u_{\mathit{N}}\end{eqnarray}$$
and a spatially invariant velocity is prescribed at the inlet of the gas phase, given as
$$\begin{eqnarray}u(x=0,h_{\mathit{N}}<y\leqslant 4h_{\mathit{N}})={\textstyle \frac{3}{2}}[1+A\sin (2\unicode[STIX]{x03C0}ft)]u_{\mathit{N}}.\end{eqnarray}$$
The co-flow in the gas phase is applied to prevent backflow at the domain outlet, which can significantly affect the computational performance as well as the accuracy of the results, but has a negligible effect on the evolution of the film flow, since the momentum of the gas phase is approximately three orders of magnitude smaller than the momentum of the liquid film. A constant film height
$h(x=0)=h_{\mathit{N}}$
is prescribed at the inlet. An open boundary condition is applied at the domain outlet, as previously used for instance by Nosoko & Miyara (Reference Nosoko and Miyara2004) and Demekhin et al. (Reference Demekhin, Kalaidin, Kalliadasis and Vlaskin2007) (Kalliadasis et al. (Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012, appendix F3) gives details on how to apply an outlet boundary condition).
3.3 LD modelling
We adopt the LD formulation corresponding to the two-field second-order model derived by Ruyer-Quil & Manneville (Reference Ruyer-Quil and Manneville1998), a set of two coupled nonlinear equations for the evolution of the interface thickness
$h(x,t)$
and local flow rate
$q(x,t)$
:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}\frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}t} & = & \displaystyle \frac{5}{6}h-\frac{5}{2}\frac{q}{h^{2}}+\unicode[STIX]{x1D6FF}\left(\frac{9}{7}\frac{q^{2}}{h^{2}}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}-\frac{17}{7}\frac{q}{h}\frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}x}\right)+\frac{5}{6}h\frac{\unicode[STIX]{x2202}^{3}h}{\unicode[STIX]{x2202}x^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}\left[4\frac{q}{h^{2}}\left(\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\right)^{2}-\frac{9}{2h}\frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}-6\frac{q}{h}\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}x^{2}}+\frac{9}{2}\frac{\unicode[STIX]{x2202}^{2}q}{\unicode[STIX]{x2202}x^{2}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}=-\frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}x},\end{eqnarray}$$
where the Shkadov scaling (Shkadov Reference Shkadov1977) has been used, giving rise to the reduced Reynolds number
$\unicode[STIX]{x1D6FF}$
defined in (2.7) and the viscous dispersion number
$\unicode[STIX]{x1D702}$
defined in (2.8). The above model is obtained by combining the long-wave expansion up to second order with a weighted residual technique based on a Galerkin projection in which the velocity field is expanded onto a basis with polynomial test functions (Ruyer-Quil & Manneville Reference Ruyer-Quil and Manneville1998, Reference Ruyer-Quil and Manneville2000, Reference Ruyer-Quil and Manneville2002) (this formulation was extended to 3D in the study by Scheid et al. (Reference Scheid, Ruyer-Quil and Manneville2006)). It is worth remarking that the model contains the second-order viscous dispersion terms (those gathered in the second line of (3.7)), which are controlled by
$\unicode[STIX]{x1D702}$
, often neglected in thin-film studies. These terms affect both the amplitude and frequency of the capillary ripples at the front of solitary waves (Ruyer-Quil & Manneville Reference Ruyer-Quil and Manneville2000). The first-order model, obtained by setting
$\unicode[STIX]{x1D702}=0$
in the second-order one already corrects the shortcomings of the first-order model obtained by Shkadov (Reference Shkadov1967), with the principal one being an erroneous prediction of the instability onset, while the second-order model is in good agreement with Orr–Sommerfeld for a sufficiently large region of
$Re$
.
Also, as was demonstrated by Pradas et al. (Reference Pradas, Tseluiko and Kalliadasis2011), who developed a coherent-structure theory for falling films, the second-order terms play an important role in the interactions between solitary pulses precisely because they affect both the amplitude and frequency of the front-running capillary ripples, and hence they are crucial for an accurate description of pulse interaction. So their influence is in fact linear, but they can have profound consequences on the nonlinear dynamics of the film and the wave-selection process in the spatiotemporal evolution. This is because solitary waves interact through their tails which overlap, i.e., the capillary ripples and their amplitude and frequency will affect the separation distance between the pulses: for instance, smaller-amplitude ripples will allow for more overlaps between the tails of neighbouring solitary waves, thus decreasing their separation distance. This in turn will affect the average separation distance between the waves when the system reaches its permanent quasiturbulent regime, and hence the density of the solitary waves.
Equations (3.7) and (3.8) are solved numerically by making use of a variable time-step Runge–Kutta method with a central finite difference technique in space. A typical time step is
$\unicode[STIX]{x0394}t=0.0025$
and the domain
$[0,L]$
with
$L=150$
is discretised into 2000 intervals. At the inlet of the system we impose an inflow boundary condition, given as
$$\begin{eqnarray}\displaystyle & q(0,t)={\textstyle \frac{1}{3}}[1+A\sin (2\unicode[STIX]{x03C0}ft)], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & h(0,t)=1, & \displaystyle\end{eqnarray}$$
and like with our DNS we impose an open-soft boundary condition at the outlet of the system to minimise any reflections (again, appendix F3 in Kalliadasis et al. (Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012) gives details on how to do this). The initial condition is given as the flat-film solution with
$h(x,0)=1$
.
3.4 Investigated case studies
We consider cases with Reynolds numbers in the range
$\mathit{Re}=5.1{-}77$
and Kapitza numbers in the range
$\mathit{Ka}=14{-}346$
with the relevant parameters given in table 1. The working fluid for the experiments is an aqueous glycerol solution with three different glycerol concentrations (by weight)
$X_{\mathit{g}}$
:
- Cases A:
$X_{\mathit{g}}=82\,\%$
,
$\unicode[STIX]{x1D70C}_{\mathit{l}}=1214~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D707}_{\mathit{l}}=7.49\times 10^{-2}~\text{Pa}~\text{s}$
and
$\unicode[STIX]{x1D70E}=0.0623~\text{N}~\text{m}^{-1}$
,- Cases B:
- $X_{\mathit{g}}=65\,\%$
,
$\unicode[STIX]{x1D70C}_{\mathit{l}}=1169~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D707}_{\mathit{l}}=1.84\times 10^{-2}~\text{Pa}~\text{s}$
and
$\unicode[STIX]{x1D70E}=0.0587~\text{N}~\text{m}^{-1}$
,
- Cases C:
- $X_{\mathit{g}}=45\,\%$
,
$\unicode[STIX]{x1D70C}_{\mathit{l}}=1113~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D707}_{\mathit{l}}=6.42\times 10^{-3}\text{Pa}~\text{s}$
and
$\unicode[STIX]{x1D70E}=0.0597~\text{N}~\text{m}^{-1}$
.
The corresponding Kapitza numbers are
$\mathit{Ka}=14$
for cases A,
$\mathit{Ka}=85$
for cases B and
$\mathit{Ka}=346$
for cases C. In all cases the inclination angle of the substrate is
$\unicode[STIX]{x1D6FD}=20^{\circ }$
with respect to the horizontal. The film is perturbed with a monochromatic, periodic change of the flow rate, with frequency
$f$
and amplitude
$A$
, applied at the inlet of the test domain. The applied forcing frequencies are well above the critical frequency, as reported by Argyriadi, Serifi & Bontozoglou (Reference Argyriadi, Serifi and Bontozoglou2004), below which parasitic pulses prevent the development of a regular wave train. Based on the classification of Ooshida (Reference Ooshida1999), all considered cases are situated in the drag-inertia regime,
$\unicode[STIX]{x1D6FF}\gtrsim 1$
.
Figure 6. Schematic illustration of the positions at which profiles of velocity and pressure gradients are analysed. Position X2 is located at the crest of the solitary wave and position X4 is located at the trough preceding the solitary wave.
Table 1. Forcing frequency and non-dimensional parameters of the analysed cases.
To allow a direct comparison of the experimental and numerical results, all cases are analysed at downstream distance
$x_{\mathit{m}}=0.256~\text{m}$
from the inlet of the test domain, as dictated by the employed experimental arrangement. The experiments are conducted first by choosing the amplitude of the monochromatic inlet forcing so that fully developed, quasistationary interface waves are obtained at the measurement position
$x_{\mathit{m}}=0.256~\text{m}$
. Subsequently, the numerical simulations are conducted using the measured fluid properties and flow rate as well as the imposed monochromatic forcing frequency and forcing amplitude in the experiments, thus establishing a direct comparison under the same conditions. The presented velocity profiles are taken at the positions illustrated in figure 6, where
$d$
is the distance between the crest of the solitary wave and its preceding trough.
Figures 7 and 8 show the spatial development of the film height and the streamwise velocity at the interface for cases A2 and C6, respectively, obtained with DNS. The figures reveal that in the studied range of Reynolds numbers the solitary waves are fully developed at the measurement position
$x_{\mathit{m}}$
. Furthermore, in both cases the difference in wave speed at the trough and the crest of the solitary wave is
${<}0.1\,\%$
, indicating that the waves have stopped growing.
Figure 7. Spatial development of the film height
$h/h_{\mathit{N}}$
and the streamwise velocity at the interface
$u_{\unicode[STIX]{x1D6F4}}/u_{\mathit{N}}$
for case A2 (
$\mathit{Re}=5.2$
), obtained with DNS. The minimum and maximum values at the measurement position (
$x_{\mathit{m}}=0.256~\text{m}$
) are shown as a reference by the dashed grey lines.
Figure 8. Spatial development of the film height
$h/h_{\mathit{N}}$
and the streamwise velocity at the interface
$u_{\unicode[STIX]{x1D6F4}}/u_{\mathit{N}}$
for case C6 (
$\mathit{Re}=77.0$
), obtained with DNS. The minimum and maximum values at the measurement position (
$x_{\mathit{m}}=0.256~\text{m}$
) are shown as a reference by the dashed grey lines.
4 Results
4.1 Comparison of experimental and numerical results
Figure 9. Instantaneous film height
$h$
, normalised with the Nusselt flat-film height
$h_{\mathit{N}}$
, for selected cases as a function of downstream distance
$x$
.
Figure 10. Instantaneous streamwise interface velocity
$u_{\unicode[STIX]{x1D6F4}}$
, normalised with the Nusselt velocity
$u_{\mathit{N}}$
, for selected cases as a function of downstream distance
$x$
. The wave speeds measured in the experiments,
$c_{Exp}$
, and the DNS,
$c_{DNS}$
, are given as well.
The experimental measurements and numerical predictions of the film height
$h$
and streamwise interface velocity
$u_{\unicode[STIX]{x1D6F4}}$
as a function of downstream distance
$x$
are shown in figures 9 and 10 for selected cases. The DNS results are generally in very good agreement with the experimental ones, both in terms of film height and interface velocity, similar to previously reported comparisons between experiments and DNS by Dietze & Ruyer-Quil (Reference Dietze and Ruyer-Quil2013), using the open-source software Gerris, and by Doro & Aidun (Reference Doro and Aidun2013) and Rohlfs, Pischke & Scheid (Reference Rohlfs, Pischke and Scheid2017), using the open-source software OpenFoam. The LD model is also in very good agreement with both experimental and DNS results provided that
$\unicode[STIX]{x1D6FF}\lesssim 12$
, but fails to capture the amplitude and frequency of the front-running capillary ripples for
$\unicode[STIX]{x1D6FF}>12$
(which in turn affect the separation distances between the solitary waves) even though it includes the second-order viscous dispersion effects. In particular, both the DNS and experimental results show fewer capillary ripples with increasing inertia than the LD model (compare, for example, cases C1 and C6 in figure 9). Such a deviation is nevertheless expected since cross-stream inertia is not negligible for
$\unicode[STIX]{x1D6FF}\gg 1$
(Kalliadasis et al.
Reference Kalliadasis, Ruyer-Quil, Scheid and Velarde2012), thus violating one of the main assumptions in the boundary-layer approximation invoked to obtain the LD formulation. Interestingly, however, the LD solution captures very well the primary solitary hump, including the maximum and minimum film heights, in all studied cases (
$\unicode[STIX]{x1D6FF}=10.3{-}110$
) – a fact not previously reported in the literature.
The maximum film height
$h_{max}$
, minimum film height
$h_{min}$
and wave speed
$c$
obtained from the experiments and DNS, shown in figure 11 for all considered cases with forcing frequency
$f=7~\text{s}^{-1}$
, are generally in satisfactory agreement with each other. In particular, the same trends can be extracted with respect to the change in film height and wave speed as
$\mathit{Re}$
increases. An increase in
$Re$
causes initially an increase in wave height, irrespective of the Kapitza number
$\mathit{Ka}$
, both with respect to the Nusselt flat-film height
$h_{\mathit{N}}$
and the film height in the preceding trough
$h_{min}$
. Eventually, the normalised maximum film height shown in figure 11(a) reaches a maximum with respect to
$\mathit{Re}$
. Increasing
$\mathit{Re}$
further ensues a decrease in maximum film height, as already noted in previous studies (Chakraborty et al.
Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014; Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016). Interestingly, the observed trend persists for the wide range of Kapitza numbers
$\mathit{Ka}$
considered in this study, with
$\mathit{Ka}=14{-}346$
in figure 11, both in the experimental measurements as well as the DNS results. The minimum film height
$h_{min}$
shows a similar yet inverse behaviour compared to the maximum film height as far as the influence of
$\mathit{Re}$
is concerned, similar to the observations reported by Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016) for falling water films.
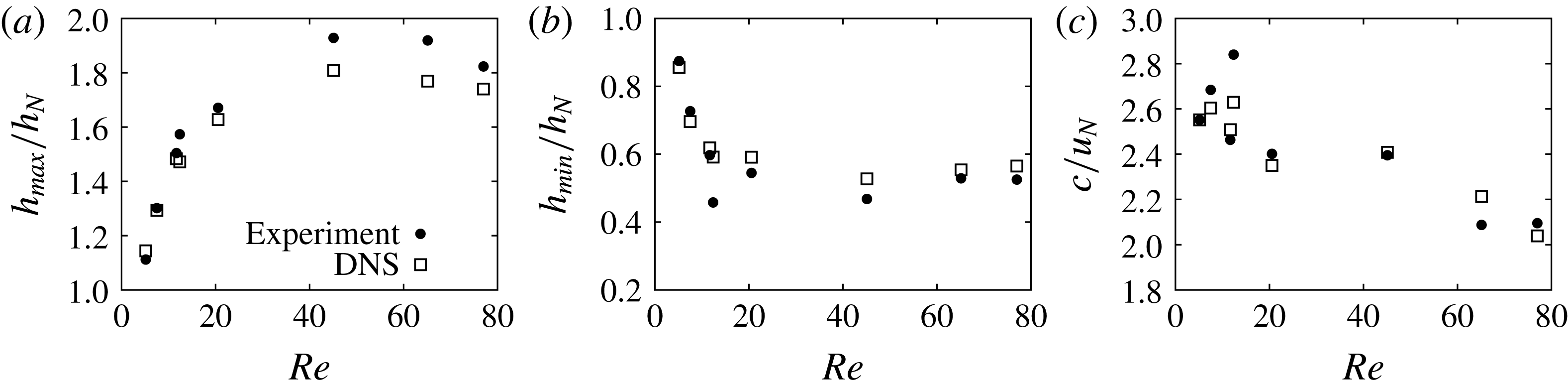
Figure 11. Maximum film height
$h_{max}/h_{\mathit{N}}$
(a), minimum film height
$h_{min}/h_{\mathit{N}}$
(b) and wave speed
$c/u_{\mathit{N}}$
(c) as a function of
$\mathit{Re}$
for cases with
$f=7~\text{s}^{-1}$
. Results obtained with the LD model are omitted in the interest of clarity.
Figure 12. Comparison of the experimental and DNS velocity profiles in the tail, at the crest and at the front of the solitary wave for selected cases, normalised with the corresponding Nusselt flat-film velocity
$u_{\mathit{N}}$
and the local film thickness
$h(x)$
. (a) In the tail of the solitary wave, see position X1 in figure 6. The circular dots indicate a semiparabolic velocity profile. (b) At the crest of the solitary wave, see position X2 in figure 6. The circular dots indicate a semiparabolic velocity profile. (c) At the front of the solitary wave, see position X3 in figure 6.
Figure 12 compares the profiles of the dimensionless streamwise velocity
$u/u_{\mathit{N}}$
in the liquid film at different positions in the solitary wave, for selected cases. The agreement between experimental measurements and DNS results is in general very good, especially for the small Reynolds numbers, cases A1 (
$\mathit{Re}=5.1$
) and B1 (
$\mathit{Re}=7.5$
). At larger Reynolds numbers the flow field is strongly dependent on the local wave shape and can vary rapidly in space, as shown by the experimental measurements of Charogiannis et al. (Reference Charogiannis, Denner, van Wachem, Kalliadasis and Markides2017) for instance. Hence, in particular at the front of the solitary wave (see figure 12
c), small differences in local film height and measurement position can lead to noticeable differences in the velocity profile. Note that the velocity profile is parabolic in the tail and underneath the crest of the solitary wave, even for the case with the highest Reynolds number (case C6,
$\mathit{Re}=77$
). This agrees with previously reported numerical results (Malamataris et al.
Reference Malamataris, Vlachogiannis and Bontozoglou2002; Gao et al.
Reference Gao, Morley and Dhir2003; Malamataris & Balakotaiah Reference Malamataris and Balakotaiah2008) and experimental measurements (Adomeit & Renz Reference Adomeit and Renz2000; Moran et al.
Reference Moran, Inumaru and Kawaji2002; Charogiannis et al.
Reference Charogiannis, An and Markides2015). Interestingly, the self-similarity of the velocity profile in the laboratory frame of reference is unaffected by the onset of a recirculation region in the moving frame when the maximum flow velocity exceeds the wave speed (for instance, in case C6). Moving further downstream to the front of the solitary wave, position X3, the velocity profile increasingly departs from the parabolic one that is observed for the tail and the crest of the solitary wave, as clearly seen in figure 12(c). The limitations of the applied PIV/PTV method to measure the velocity fields in our experimental arrangement prohibit a direct comparison of the velocity profiles obtained experimentally with those from DNS in the trough of the solitary wave (position X4).
In summary, carefully conducted experiments and DNS using state-of-the-art methods show good agreement when predicting harmonically excited solitary waves on falling liquid films in the inertia-dominated regime and not only for flows with small Reynolds numbers reported in previous studies (for example, Gao et al. (Reference Gao, Morley and Dhir2003), Dietze & Ruyer-Quil (Reference Dietze and Ruyer-Quil2013)). Note that this comparison of experiments and DNS is more detailed than previously published comparisons (notably Dietze & Ruyer-Quil (Reference Dietze and Ruyer-Quil2013), Doro & Aidun (Reference Doro and Aidun2013), Rohlfs et al. (Reference Rohlfs, Pischke and Scheid2017)), as it comprises the film height, film velocity at the interface, the velocity profile in the liquid film at different positions, and the wave speed, across a range of Reynolds and Kapitza numbers. This allows one to draw conclusions based collectively on both the experimental measurements and the DNS results. And although the LD model is applied outside what is usually considered to be its range of validity (
$\unicode[STIX]{x1D6FF}\lesssim 10$
), its predictive accuracy with respect to the maximum and minimum film height, and consequently the wave height, is impressive and somewhat unexpected. This might be explained by the predominantly parabolic velocity profile in the tail and underneath the crest of the solitary wave, which accounts for the largest part of the solitary wave, even after the onset of flow recirculation.
4.2 Mechanism for stabilising the wave height
A reduction of the maximum film height with increasing
$\mathit{Re}$
is observed in figure 11(a) in the experimental measurements as well as the DNS results. Chakraborty et al. (Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014) also reported a reducing maximum film height in their DNS results of a liquid film (
$\mathit{Ka}=193{-}10\,000$
) with a single solitary wave on a vertical substrate, for sufficiently high reduced Reynolds numbers
$\unicode[STIX]{x1D6FF}$
. Similarly, Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016) reported a stagnation of the maximum film height for sufficiently high Reynolds numbers on substrates with different inclination angles
$\unicode[STIX]{x1D6FD}=45^{\circ }{-}90^{\circ }$
and using fluids with different surface tension coefficients. Extending the balance of gravity and viscous stresses (which forms the basis of the Nusselt flat-film solution) to wavy films, the film height is related to the Reynolds number as
$h\sim \sqrt[3]{\mathit{Re}}$
. Thus, the wave height should increase with increasing Reynolds number, instead of stagnating or even reducing, as suggested by the presented numerical results and experimental measurements. Surface tension stabilises the wave, yet the absolute value of the interface curvature of the main wave hump is decreasing for increasing Reynolds number once the wave height does not further increase, since the wavelength of the solitary wave is
$\unicode[STIX]{x1D706}\sim \sqrt{\mathit{Re }\sin \unicode[STIX]{x1D6FD}}$
(Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016). Hence, the surface tension acting on the solitary wave decreases with increasing
$\mathit{Re}$
. Consequently, there must be an alternative mechanism acting to stabilise the height of the solitary wave against the destabilising effect of the increased inertia.
Figure 13 shows the maximum film height
$h_{max}$
, normalised by the Nusselt height
$h_{\mathit{N}}$
, alongside the corresponding maximum flow rate
$q_{max}$
, normalised by the Nusselt flow rate
$q_{\mathit{N}}$
, for cases with
$\mathit{Ka}=346$
(cases C) and
$f=10~\text{s}^{-1}$
, in the Reynolds number range
$\mathit{Re}=10{-}85$
, obtained with DNS. The instantaneous local flow rate is defined as
$$\begin{eqnarray}q(x)=\int _{0}^{h(x)}u(x)\,\text{d}y,\end{eqnarray}$$
where
$h(x)$
and
$u(x)$
are the local film height and flow velocity, respectively. Both
$h_{max}/h_{\mathit{N}}$
and
$q_{max}/q_{\mathit{N}}$
exhibit a clear maximum with respect to the Reynolds number at
$\mathit{Re}_{\mathit{c}}\approx 50$
, and decrease for further increasing Reynolds number
$\mathit{Re}>\mathit{Re}_{\mathit{c}}$
, as is evident in figure 13. A similar behaviour is observed comparing
$h_{max}/h_{\mathit{N}}$
and
$q_{max}/q_{\mathit{N}}$
of a water film falling on a vertical substrate, as previously considered by Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), shown in figure 14. Charogiannis et al. (Reference Charogiannis, Denner, van Wachem, Kalliadasis and Markides2017) recently established a linear relationship between local flow rate and local film height for a given solitary wave, with a slope that corresponds to the wave speed. Hence, the simultaneous increase and decrease of
$h_{max}/h_{\mathit{N}}$
and
$q_{max}/q_{\mathit{N}}$
observed in figures 13 and 14 is to be expected. Moreover, the shape of the solitary wave is governed by the balance of inertia, represented by the dynamic pressure
$p_{dyn}=\unicode[STIX]{x1D70C}u^{2}/2$
, and surface tension, represented by the capillary pressure
$p_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70E}/h_{N}$
(Denner et al.
Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016). The relevant characteristic parameter is, thus, the Weber number
$\mathit{We}=2p_{dyn}/p_{\unicode[STIX]{x1D70E}}$
(see (2.4)), which can be rewritten with respect to position
$x$
as
$$\begin{eqnarray}\mathit{We}(x)=\frac{\unicode[STIX]{x1D70C}_{\mathit{l}}q(x)^{2}}{\unicode[STIX]{x1D70E}h(x)}\end{eqnarray}$$
based on the local flow rate given in (4.1). Since the density
$\unicode[STIX]{x1D70C}_{\mathit{l}}$
and surface tension coefficient
$\unicode[STIX]{x1D70E}$
are assumed to be constant, a change in flow rate leads to a change in film height at a given Weber number. Note that the dynamic pressure
$p_{dyn}$
represents the (streamwise) translational kinetic energy
$E_{u}=m\boldsymbol{u}^{2}/2$
per unit volume of the liquid film, where
$m$
is the fluid mass.
Figure 13. Maximum film height
$h_{max}$
(a) and maximum flow rate
$q_{max}$
(b), normalised by the corresponding Nusselt solution, as a function of Reynolds number
$\mathit{Re}$
for case C with
$f=10~\text{s}^{-1}$
, obtained with DNS.
Figure 14. Maximum film height
$h_{max}$
(a) and maximum flow rate
$q_{max}$
(b), normalised by the corresponding Nusselt solution, as a function of Reynolds number
$\mathit{Re}$
for a falling water film on a vertical substrate, as previously considered in Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), obtained with DNS.
Figure 15. Maximum flow rate
$q_{max}$
(a) and relative velocity
$u_{max}-c$
(b), normalised by the corresponding Nusselt solution, as a function of maximum film height
$h_{max}$
for case C with
$f=10~\text{s}^{-1}$
in the range
$\mathit{Re}=10{-}85$
, obtained with DNS. The colour scale represents the Reynolds number.
A plot of the maximum film height against the maximum flow rate, presented in figure 15(a), confirms the correlation between
$h_{max}/h_{\mathit{N}}$
and
$q_{max}/q_{\mathit{N}}$
established above, but it also shows a reduction of the maximum flow rate corresponding to a given maximum film height for
$\mathit{Re}>\mathit{Re}_{\mathit{c}}$
. This difference between
$q_{max}$
at a given
$h_{max}$
for
$\mathit{Re}<\mathit{Re}_{\mathit{c}}$
and the corresponding
$q_{max}$
for
$\mathit{Re}>\mathit{Re}_{\mathit{c}}$
suggests a reduction of the effective inertia acting on the solitary wave for
$\mathit{Re}>\mathit{Re}_{\mathit{c}}$
, with
$\mathit{Re}_{\mathit{c}}\approx 50$
for the conditions analysed in figure 15(a). Interestingly, this reduction of effective inertia coincides with the development of flow recirculation in the main wave hump with respect to the moving frame of reference when the maximum flow velocity surpasses the wave speed,
$u_{max}>c$
, as observed in figure 15(b). The flow recirculation in the moving frame of reference increases the angular velocity
$\unicode[STIX]{x1D734}$
and, as a result, increases the angular kinetic energy
$E_{\unicode[STIX]{x1D6FA}}=I\unicode[STIX]{x1D734}^{2}/2$
, where
$I$
is the moment of inertia. Due to the conservation of energy, the increase of angular kinetic energy
$E_{\unicode[STIX]{x1D6FA}}$
reduces the translational kinetic energy
$E_{u}$
. This transfer of energy leads to the observed reduction in effective inertia of the film flow. It is worth noting that the increase in
$\unicode[STIX]{x1D734}$
corresponds to an increase in vorticity
$\unicode[STIX]{x1D74E}=2\unicode[STIX]{x1D734}$
(assuming incompressible flow and neglecting high-order contributions). However, an analysis of the vorticity distribution in the solitary waves of the considered cases has not provided conclusive evidence that the increase in viscous dissipation plays a significant part in the observed reduction of the effective inertia acting on the solitary wave. Note that for the flow conditions studied in figure 15, a theoretical criterion derived by Rohlfs & Scheid (Reference Rohlfs and Scheid2015) predicts the onset of flow recirculation for
$\mathit{Re}_{circ}\approx 20$
, which is in reasonable agreement with the observed onset of flow recirculation at
$\mathit{Re}_{circ}\approx 25$
. A possible explanation for this difference in
$\mathit{Re}_{circ}$
is the reduced bulk velocity compared to the Nusselt solution for increasing wave height reported by Charogiannis et al. (Reference Charogiannis, Denner, van Wachem, Kalliadasis and Markides2017), that shifts the critical local flow rate for the onset of flow recirculation to a higher Reynolds number.
Figure 16. Cross-stream velocity
$v$
, normalised by the Nusselt velocity
$u_{\mathit{N}}$
, of case C with
$f=10~\text{s}^{-1}$
for
$\mathit{Re}\in \{10,30,60\}$
, obtained with DNS. No flow recirculation in the moving frame of reference is observed for
$\mathit{Re}=10$
(
$c>u_{max}$
), but flow recirculation is present for
$\mathit{Re}=30$
and
$\mathit{Re}=60$
(
$c<u_{max}$
). Note that the limits of the colour scale (
$-0.01\geqslant v/u_{\mathit{N}}\geqslant 0.01$
) do not represent the min/max values of the cross-stream velocity.
Aside from the reduction of (streamwise) translational kinetic energy, the onset of flow recirculation in the moving frame of reference also leads to a downward motion (in the wall direction) of the flow in the main wave hump. Before the onset of flow recirculation, the propagation of the solitary wave with
$c>u_{max}$
leads to an upward motion (away from the wall) downstream of the wave crest, as observed in figure 16(a). However, after the onset of flow recirculation (
$c<u_{max}$
), the flow moves downwards under the crest and upwards in the tail of the solitary wave, as observed in figure 16(b,c) and as a consequence of the flow recirculation. This change in cross-stream motion contributes to the observed saturation of the film height after the onset of flow recirculation. In general, this effect is similar to the long-wave instability mechanism that generates the solitary waves; at the onset of the instability, the phase difference between vorticity and the instability wave is destabilising if
$c>u_{max}$
, yet it is stabilising if
$c<u_{max}$
(Kelly et al.
Reference Kelly, Goussis, Lin and Hsu1989). This mechanism suggests that, in general, the fluid motion in the bulk phase has a stabilising effect when
$c<u_{max}$
(i.e. flow recirculation in the moving frame of reference), as confirmed by the presented results.
In summary, the presented results show that the flow recirculation in the moving frame of reference is responsible for the stabilisation, or even reduction, of the height of the solitary waves at large Reynolds numbers. The flow rate and the maximum velocity in the film exhibit their highest values at (approximately) the same Reynolds number at which the film height reaches its maximum. With respect to the link between film height and flow rate, this is to be expected based on the recent study of Charogiannis et al. (Reference Charogiannis, Denner, van Wachem, Kalliadasis and Markides2017), reporting a linear relationship between film height and flow rate. However, the connection of the film height (and flow rate) with the maximum flow velocity and the recirculation in the moving frame of reference has not been reported before. This finding is of particular interest for the optimisation of the heat and mass transport characteristics of wavy falling liquid films, which has previously been shown to be critically dependent on the characteristics of the solitary waves (Mathie et al. Reference Mathie, Nakamura and Markides2013; Markides et al. Reference Markides, Mathie and Charogiannis2015) and with flow recirculation in the moving frame of reference typically improving the heat and mass transfer within the liquid film (Roberts & Chang Reference Roberts and Chang2000; Albert et al. Reference Albert, Marschall and Bothe2014).
4.3 Flow reversal
Flow reversal is driven by a strong positive streamwise pressure gradient that results from the rapid change in interface curvature between a solitary wave and its preceding capillary ripple (Dietze et al. Reference Dietze, Leefken and Kneer2008, Reference Dietze, Al-Sibai and Kneer2009) or its preceding solitary wave (Doro & Aidun Reference Doro and Aidun2013). Furthermore, previous studies (Dietze et al. Reference Dietze, Leefken and Kneer2008, Reference Dietze, Al-Sibai and Kneer2009; Doro & Aidun Reference Doro and Aidun2013; Rohlfs & Scheid Reference Rohlfs and Scheid2015) found that a larger magnitude of the interface curvature in the trough and at the preceding capillary ripple, as well as a higher inclination angle of the substrate, favour the onset of flow separation and reversal. However, Chakraborty et al. (Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014) reported that flow reversal is limited by lower and upper limits with respect to the (reduced) Reynolds number.
The profiles of velocity and streamwise pressure gradient for cases B4 and C2, with a Reynolds number of
$\mathit{Re}=26.9$
and
$\mathit{Re}=28.5$
, respectively, and a forcing frequency of
$f=10~\text{s}^{-1}$
, are shown in figure 17. The higher inertia relative to surface tension of case B4 (
$\mathit{We}=1.98$
) compared to case C2 (
$\mathit{We}=0.53$
) means the high pressure gradient is concentrated near the interface in case B4, whereas in case C2 the region of high pressure gradient extends to the wall. As a result, flow reversal is observed in case B4 but not in case C2. This happens although the curvature of the trough in cases B4 and C2 is comparable, with
$\unicode[STIX]{x1D705}_{min}=-860~\text{m}^{-1}$
in case B4 and
$\unicode[STIX]{x1D705}_{min}=-878~\text{m}^{-1}$
in case C2, and the difference in surface tension between the two cases is merely
$2\,\%$
. Hence, the interface curvature can be ruled out as the source of the observed differences, indicating that the larger influence of inertia compared to surface tension of case B4 (higher
$\mathit{We}$
) is the dominating factor. A similar behaviour can be observed in figure 17 for cases B2 (
$\mathit{We}=0.49$
) and C1 (
$\mathit{We}=0.13$
), which have a Reynolds number of
$\mathit{Re}=11.7$
and
$\mathit{Re}=12.4$
, respectively, where flow reversal is observed in case C1 but not in case B2.
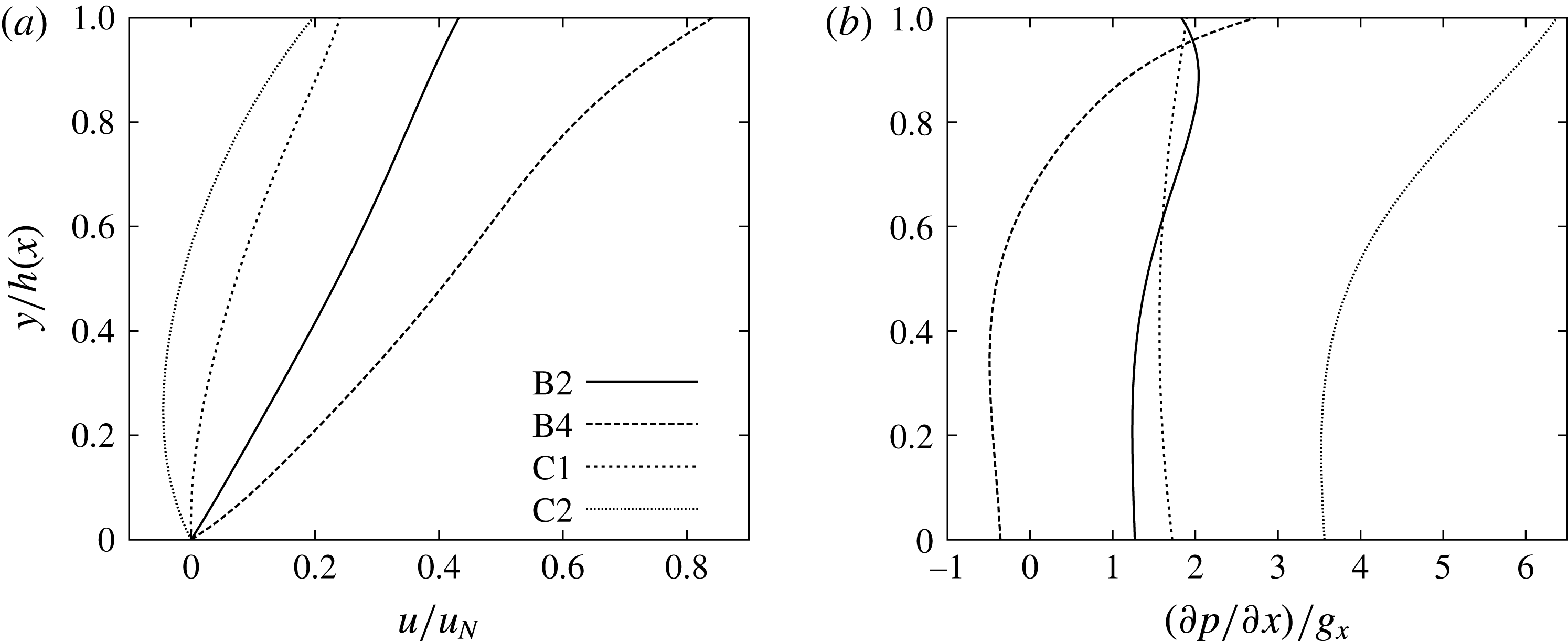
Figure 17. DNS profiles of the streamwise velocity
$u/u_{\mathit{N}}$
(a) and the streamwise pressure gradient (b), normalised with the streamwise component of gravity
$g_{x}$
, at the trough preceding the solitary wave, position X4, for cases B2 (
$\mathit{Re}=11.7$
,
$f=7~\text{s}^{-1}$
), B4 (
$\mathit{Re}=26.9$
,
$f=10~\text{s}^{-1}$
), C1 (
$\mathit{Re}=12.4$
,
$f=7~\text{s}^{-1}$
) and C2 (
$\mathit{Re}=28.5$
,
$f=10~\text{s}^{-1}$
), obtained with DNS.
Interestingly, the magnitude of the flow reversal region as well as the size of the separation eddy are considerably larger in case C2 than in case C1, although the forcing frequency and the Froude number
$\mathit{Fr}=\sqrt{3\mathit{Re }/\cot \unicode[STIX]{x1D6FD}}$
, which is
$\mathit{Fr}=3.7$
for case C1 and
$\mathit{Fr}=5.6$
for case C2, mean flow separation should be less likely in case C2, based on findings of previous studies (Chakraborty et al.
Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014; Rohlfs & Scheid Reference Rohlfs and Scheid2015). The front of the main wave hump in case C2 (
$d/h_{\mathit{N}}=4.79$
) is significantly steeper than in case C1 (
$d/h_{\mathit{N}}=7.55$
), also seen in figure 18, leading to a considerable increase in negative streamwise pressure gradient immediately upstream of the wave trough, which generally counteracts flow separation. However, the shorter wavelength combined with the higher Reynolds number of case C2 (
$\unicode[STIX]{x1D706}/h_{\mathit{N}}=39.7$
,
$\mathit{Re}=28.5$
) compared to case C1 (
$\unicode[STIX]{x1D706}/h_{\mathit{N}}=52.3$
,
$\mathit{Re}=12.4$
), leads to larger capillary waves for case C2. As a result, the pressure underneath the first capillary ripple is noticeably higher in case C2 than in case C1, as observed in figure 18, which results in a larger streamwise pressure gradient between the trough preceding the main wave hump and the crest of the first capillary ripple, and, consequently, promotes flow separation and reversal. The effect of the pressure changes in the streamwise direction on the velocity underneath the trough can clearly be seen by the strongly curved and clustered isocontours of the streamwise velocity in figure 18.
Figure 18. Pressure contours and isocontours of the streamwise velocity
$u/u_{N}\in \{0,0.1,0.2,0.3,0.5,0.7,1,1.5,2\}$
in the liquid film of cases C1 and C2, obtained with DNS. In both cases a streamwise section of 0.04 m is shown.
In the above cases, the low-pressure region underneath the wave trough cannot extend to the low-velocity region near the wall in cases where inertia is high compared to surface tension, limiting the high streamwise pressure gradients to the close vicinity of the interface. Hence, the substantially reduced streamwise pressure gradient near the wall is not able to initiate flow separation, i.e. the direction of the flow remains unchanged. In addition, the front of the solitary wave becomes steeper as the Reynolds number increases (Denner et al. Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), which increases the curvature of the wave trough and leads to a larger streamwise pressure gradient underneath the trough that promotes flow reversal. Yet, the steeper front of the solitary wave also increases the pressure difference between the main hump and the wave trough, as observed in figure 18. Thus, flow reversal is eventually arrested when the Reynolds number is sufficiently high, because the (negative) pressure gradient upstream of the wave trough dominates the (positive) pressure gradient downstream of the wave trough. As a consequence, the parameter space in which flow reversal occurs is governed by a non-trivial interplay of a variety of parameters, including inclination angle and frequency, as suggested by previous studies (Chakraborty et al. Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014; Rohlfs & Scheid Reference Rohlfs and Scheid2015), as well as wave steepness, the size of capillary ripples and the balance of inertia and surface tension.
5 Conclusions
Falling liquid films exhibit rich spatiotemporal dynamics governed by a complex interplay between inertia, viscosity, surface tension and gravity. Despite several decades of intensive research, this interplay is not fully understood and important aspects of falling film dynamics, especially for inertia-dominated falling films, have not yet been resolved. In this study we undertook a systematic investigation comprising advanced computations and experimentation aimed at addressing open questions associated with the inertia–capillary interactions that govern the shape and propagation of solitary waves on falling liquid films in the inertia-dominated regime.
The overall agreement between experiments and DNS is very good for all quantities of interest, such as film thickness, velocity profile and interface velocity, and within the expectations based on the experimental tolerances and the numerical assumptions. The applied LD model also performs very well and shows excellent agreement with experiments and DNS for reduced Reynolds numbers
$\unicode[STIX]{x1D6FF}\lesssim 12$
. For higher
$\unicode[STIX]{x1D6FF}$
the results of the LD model increasingly deviate from the experimental measurements and DNS results, which can be attributed to the boundary-layer approximation on which the LD model is founded; for instance, LD models are not able to predict the pressure fields shown in figure 18 that also include a significant hydrodynamic (due to the complex flow field) contribution. Nevertheless, the LD model is able to predict accurately the maximum and minimum film heights even for inertia-dominated flows with
$\unicode[STIX]{x1D6FF}\gg 12$
, a previously unknown, very useful and interesting feature of LD models. A possible explanation for this behaviour of LD models is the parabolic velocity profile in most parts of the film, in particular under the crest of solitary waves (and even in the inertia-dominated regime and after the onset of flow recirculation).
Careful interrogation of the wave characteristics shows a stagnation/reduction of the maximum film height at high Reynolds numbers. While in the present study, as well as in the previous study of Denner et al. (Reference Denner, Pradas, Charogiannis, Markides, van Wachem and Kalliadasis2016), this stagnation/reduction of the maximum film height has been observed for trains of travelling solitary waves with constant forcing frequency, a similar behaviour was reported by Chakraborty et al. (Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014) for a single solitary wave travelling on an otherwise flat film (corresponding to an infinite wavelength). The presented results reveal that this reduction in maximum film height coincides with a reduction in the maximum flow rate and suggest that a reduction of the effective inertia acting on the solitary wave hump is responsible for the stagnation/reduction of the height of solitary waves at high Reynolds numbers. This reduction of effective inertia is found to be the result of flow recirculation in the main wave hump in the moving frame of reference. The observed maximum in flow rate at a critical Reynolds number, which coincides with the maximum film height, is an important finding as far as exploitation of falling liquid films for heat and mass transfer applications is concerned, since previous studies (Roberts & Chang Reference Roberts and Chang2000; Mathie et al. Reference Mathie, Nakamura and Markides2013; Albert et al. Reference Albert, Marschall and Bothe2014; Markides et al. Reference Markides, Mathie and Charogiannis2015) suggested a significant impact of the film height, the flow rate and the recirculation on the heat and mass transfer characteristics of film flows. Regardless of the Reynolds number and regardless of whether or not flow recirculation in the moving frame is present, the velocity profile in the tail of the solitary waves and underneath the wave crest is found in both the experiments and DNS to have a parabolic, self-similar shape.
At the trough preceding the solitary wave, the velocity profile is strongly influenced by the low-pressure region underneath the trough, due to the convex shape of the interface and the resulting positive pressure gradient downstream of the trough. If the conditions are favourable, the flow underneath the trough preceding the solitary wave separates from the wall and flow reversal ensues. However, for sufficiently high inertia, the streamwise pressure gradient from the convex interface shape cannot reach the low-velocity region near the wall; thus, the magnitude of the streamwise pressure gradient is insufficient to initiate flow separation and flow reversal. This agrees with the observation of an upper limit for the flow reversal with respect to the Reynolds number reported, albeit without studying the underlying mechanism in detail, by Chakraborty et al. (Reference Chakraborty, Nguyen, Ruyer-Quil and Bontozoglou2014). In addition to inertia, our results also confirm that the pressure resulting from the curvature of the first capillary ripple is a dominant factor for the flow separation observed in front of the solitary wave, as initially proposed by Dietze et al. (Reference Dietze, Leefken and Kneer2008). The change in flow direction associated with the flow reversal occurring underneath the wave trough may enhance the heat and mass transport characteristics and, hence, understanding the reasons underpinning the upper (and lower) limit of flow reversal with respect to the Reynolds number is of direct practical relevance.
Acknowledgements
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) through grant nos. EP/K008595/1 and EP/M021556/1. Data supporting this publication can be obtained on request from cep-lab@imperial.ac.uk.
Open access
