1. Introduction
Sparse identification of nonlinear dynamics (SINDy) (Brunton, Proctor & Kutz Reference Brunton, Proctor and Kutz2016a) is one of the prominent data-driven tools to obtain governing equations of nonlinear dynamics in a form that we can understand. The SINDy algorithm enables us to discover a governing equation from time-discretized data and identify dominant terms from a large set of potential terms that are likely to be involved in the model. Recently, the usefulness of the SINDy has been demonstrated in various fields (Champion, Brunton & Kutz Reference Champion, Brunton and Kutz2019b; Hoffmann, Fröhner & Noé Reference Hoffmann, Fröhner and Noé2019; Zhang & Schaeffer Reference Zhang and Schaeffer2019; Deng et al. Reference Deng, Noack, Morzyński and Pastur2020). Here, let us introduce some efforts, especially in the fluid dynamics community. Loiseau, Noack & Brunton (Reference Loiseau, Noack and Brunton2018b) utilized SINDy to present general reduced-order modelling (ROM) framework for experimental data: sensor data and particle image velocimetry data. The model was investigated using a transient and post-transient laminar cylinder wake. They reported that the nonlinear full-state dynamics can be modelled with sensor-based dynamics and SINDy-based estimation for coefficients of ROM. The SINDy which takes into account control inputs (called SINDYc) was also investigated by Brunton, Proctor & Kutz (Reference Brunton, Proctor and Kutz2016b) using the Lorenz equations. Loiseau & Brunton (Reference Loiseau and Brunton2018) combined SINDy and proper orthogonal decomposition (POD) to enforce energy-preserving physical constraints in the regression procedure toward the development of a new data-driven Galerkin regression framework. For the time-varying aerodynamics, Li et al. (Reference Li, Kaiser, Laima, Li, Brunton and Kutz2019) identified vortex-induced vibrations on a long-span suspension bridge utilizing the SINDy algorithm extended to parametric partial differential equations (Rudy et al. Reference Rudy, Brunton, Proctor and Kutz2017). As a novel method to perform the order reduction of data and SINDy simultaneously, there is a customized autoencoder (AE) (Champion et al. Reference Champion, Lusch, Kutz and Brunton2019a) introducing the SINDy loss in the loss function of deep AE networks. The sparse regression idea has also recently been propagated to turbulence closure modelling purposes (Beetham & Capecelatro Reference Beetham and Capecelatro2020; Schmelzer, Dwight & Cinnella Reference Schmelzer, Dwight and Cinnella2020; Beetham, Fox & Capecelatro Reference Beetham, Fox and Capecelatro2021; Duraisamy Reference Duraisamy2021). As reported in these studies, by employing the SINDy to predict the temporal evolution of a system, we can obtain ordinary differential equations, which should be helpful to many applications, e.g. control of a system. In this way, the propagation of the use of SINDy can be seen in the fluid dynamics community.
We here examine the possibility of SINDy-based modelling of low-dimensionalized complex fluid flows presented in figure 1. Following our preliminary tests with the van der Pol oscillator and the Lorenz attractor presented in the Appendices, we apply the SINDys with two regression methods, (1) thresholded least square algorithm (TLSA) and (2) adaptive least absolute shrinkage and selection operator (Alasso), to a two-dimensional cylinder wake at ![]() $Re_D=100$, its transient process, and a wake of two-parallel cylinders as examples of high-dimensional dynamics. In this study, a convolutional neural network-based autoencoder (CNN-AE) is utilized to handle these high dimensional data with SINDy whose library matrix is suitable for low-dimensional variable combinations (Kaiser, Kutz & Brunton Reference Kaiser, Kutz and Brunton2018). The CNN-AE here is employed to map a high-dimensional dynamics into low-dimensional latent space. The SINDy is then utilized to obtain a governing equation of the mapped low-dimensional latent vector. Unifying the dynamics of the latent vector obtained via SINDy with the CNN decoder which can remap the low-dimensional latent vector to the original dimension, we can present the temporal evolution of high-dimensional dynamics and avoid the issue with high-dimensional variables as discussed above. The scheme of the present ROM is inspired by Hasegawa et al. (Reference Hasegawa, Fukami, Murata and Fukagata2019, Reference Hasegawa, Fukami, Murata and Fukagata2020a,Reference Hasegawa, Fukami, Murata and Fukagatab) who utilized a long short term memory instead of SINDy in the present ROM framework. The paper is organized as follows. We provide details of SINDy and CNN-AE in § 2. We present the results for high-dimensional flow examples with the CNN-AE/SINDy ROM in §§ 3.1, 3.2 and 3.3. In § 3.4, we also discuss its applicability to turbulence using the nine-equation turbulent shear flow model, although without considering the CNN-AE. At last, concluding remarks with outlook are offered in § 4.
$Re_D=100$, its transient process, and a wake of two-parallel cylinders as examples of high-dimensional dynamics. In this study, a convolutional neural network-based autoencoder (CNN-AE) is utilized to handle these high dimensional data with SINDy whose library matrix is suitable for low-dimensional variable combinations (Kaiser, Kutz & Brunton Reference Kaiser, Kutz and Brunton2018). The CNN-AE here is employed to map a high-dimensional dynamics into low-dimensional latent space. The SINDy is then utilized to obtain a governing equation of the mapped low-dimensional latent vector. Unifying the dynamics of the latent vector obtained via SINDy with the CNN decoder which can remap the low-dimensional latent vector to the original dimension, we can present the temporal evolution of high-dimensional dynamics and avoid the issue with high-dimensional variables as discussed above. The scheme of the present ROM is inspired by Hasegawa et al. (Reference Hasegawa, Fukami, Murata and Fukagata2019, Reference Hasegawa, Fukami, Murata and Fukagata2020a,Reference Hasegawa, Fukami, Murata and Fukagatab) who utilized a long short term memory instead of SINDy in the present ROM framework. The paper is organized as follows. We provide details of SINDy and CNN-AE in § 2. We present the results for high-dimensional flow examples with the CNN-AE/SINDy ROM in §§ 3.1, 3.2 and 3.3. In § 3.4, we also discuss its applicability to turbulence using the nine-equation turbulent shear flow model, although without considering the CNN-AE. At last, concluding remarks with outlook are offered in § 4.

Figure 1. Covered examples of fluid flows in the present study.
2. Methods
2.1. SINDy
Sparse identification of nonlinear dynamics (Brunton et al. Reference Brunton, Proctor and Kutz2016a) is performed to identify nonlinear governing equations from time series data in the present study. The temporal evolution of the state ![]() $\boldsymbol {x}(t)$ in a typical dynamical system can often be represented in the form of an ordinary differential equation,
$\boldsymbol {x}(t)$ in a typical dynamical system can often be represented in the form of an ordinary differential equation,
To explain the SINDy algorithm, let ![]() $\boldsymbol {x}(t)$ be
$\boldsymbol {x}(t)$ be ![]() $(x(t),y(t))$ hereinafter, although the SINDy can also handle the dynamics with higher dimensions, as will be considered later. First, the temporally discretized data of
$(x(t),y(t))$ hereinafter, although the SINDy can also handle the dynamics with higher dimensions, as will be considered later. First, the temporally discretized data of ![]() $\boldsymbol {x}$ are collected to arrange a data matrix
$\boldsymbol {x}$ are collected to arrange a data matrix ![]() $\boldsymbol {X}$,
$\boldsymbol {X}$,
 \begin{equation} \boldsymbol{X}= \left( \begin{array}{c} \boldsymbol{x}^{T}(t_1) \\ \boldsymbol{x}^{T}(t_2) \\ \vdots \\ \boldsymbol{x}^{T}(t_m)\end{array} \right) = \left( \begin{array}{cc} x(t_1) & y(t_1) \\ x(t_2) & y(t_2) \\ \vdots & \vdots \\ x(t_m) & y(t_m) \end{array} \right). \end{equation}
\begin{equation} \boldsymbol{X}= \left( \begin{array}{c} \boldsymbol{x}^{T}(t_1) \\ \boldsymbol{x}^{T}(t_2) \\ \vdots \\ \boldsymbol{x}^{T}(t_m)\end{array} \right) = \left( \begin{array}{cc} x(t_1) & y(t_1) \\ x(t_2) & y(t_2) \\ \vdots & \vdots \\ x(t_m) & y(t_m) \end{array} \right). \end{equation}
We then collect the time series data of the time-differentiated value ![]() $\dot {\boldsymbol x}(t)$ to construct a time-differentiated data matrix
$\dot {\boldsymbol x}(t)$ to construct a time-differentiated data matrix ![]() $\dot {\boldsymbol {X}}$,
$\dot {\boldsymbol {X}}$,
 \begin{equation} \dot{\boldsymbol{X}}= \left( \begin{array}{c} \dot{\boldsymbol{x}}^{T}(t_1) \\ \dot{\boldsymbol{x}}^{T}(t_2) \\ \vdots \\ \dot{\boldsymbol{x}}^{T}(t_m) \end{array} \right) = \left( \begin{array}{cc} \dot{x}(t_1) & \dot{y}(t_1) \\ \dot{x}(t_2) & \dot{y}(t_2) \\ \vdots & \vdots \\ \dot{x}(t_m) & \dot{y}(t_m)\end{array} \right). \end{equation}
\begin{equation} \dot{\boldsymbol{X}}= \left( \begin{array}{c} \dot{\boldsymbol{x}}^{T}(t_1) \\ \dot{\boldsymbol{x}}^{T}(t_2) \\ \vdots \\ \dot{\boldsymbol{x}}^{T}(t_m) \end{array} \right) = \left( \begin{array}{cc} \dot{x}(t_1) & \dot{y}(t_1) \\ \dot{x}(t_2) & \dot{y}(t_2) \\ \vdots & \vdots \\ \dot{x}(t_m) & \dot{y}(t_m)\end{array} \right). \end{equation}
In the present study, the time-differentiated values are obtained with the second-order central-difference scheme. Note in passing that results in the present study are not sensitive to the differential scheme with appropriate time steps for construction of ![]() $\dot {\boldsymbol X}$. Then, we prepare a library matrix
$\dot {\boldsymbol X}$. Then, we prepare a library matrix ![]() $\varTheta (\boldsymbol {X})$ including nonlinear terms of
$\varTheta (\boldsymbol {X})$ including nonlinear terms of ![]() $\boldsymbol {X}$,
$\boldsymbol {X}$,
 \begin{equation} \varTheta (\boldsymbol{X}) = \left( \begin{array}{cccccc} | & | & | & | & | & | \\ 1 & \boldsymbol{X} & \boldsymbol{X}^{P_2} & \boldsymbol{X}^{P_3} & \boldsymbol{X}^{P_4} & \boldsymbol{X}^{P_5} \\ | & | & | & | & | & | \end{array} \right), \end{equation}
\begin{equation} \varTheta (\boldsymbol{X}) = \left( \begin{array}{cccccc} | & | & | & | & | & | \\ 1 & \boldsymbol{X} & \boldsymbol{X}^{P_2} & \boldsymbol{X}^{P_3} & \boldsymbol{X}^{P_4} & \boldsymbol{X}^{P_5} \\ | & | & | & | & | & | \end{array} \right), \end{equation}
where ![]() $\boldsymbol {X}^{P_i}$ is
$\boldsymbol {X}^{P_i}$ is ![]() $i$th-order polynomials constructed by
$i$th-order polynomials constructed by ![]() $x$ and
$x$ and ![]() $y$. The set of nonlinear potential terms here includes up to fifth-order terms, although what terms are included can be arbitrarily set. We finally determine a coefficient matrix
$y$. The set of nonlinear potential terms here includes up to fifth-order terms, although what terms are included can be arbitrarily set. We finally determine a coefficient matrix ![]() $\varXi$,
$\varXi$,
 \begin{equation} \varXi = (\xi_x \quad \xi_y) = \left( \begin{array}{cc} \xi _{(x,\ 1)} & \xi _{(y,\ 1)} \\ \xi _{(x,\ 2)} & \xi _{(y,\ 2)} \\ \vdots & \vdots \\ \xi _{(x,\ l)} & \xi _{(y,\ l)}\end{array} \right), \end{equation}
\begin{equation} \varXi = (\xi_x \quad \xi_y) = \left( \begin{array}{cc} \xi _{(x,\ 1)} & \xi _{(y,\ 1)} \\ \xi _{(x,\ 2)} & \xi _{(y,\ 2)} \\ \vdots & \vdots \\ \xi _{(x,\ l)} & \xi _{(y,\ l)}\end{array} \right), \end{equation}in the state equation,
using an arbitrary regression method, such as TLSA, least absolute shrinkage and selection operator (Lasso) and so on. The subscript ![]() $l$ in (2.5) denotes the row index of the library matrix. Once the coefficient matrix
$l$ in (2.5) denotes the row index of the library matrix. Once the coefficient matrix ![]() $\varXi$ is obtained, the governing equation is identified as
$\varXi$ is obtained, the governing equation is identified as
In this study, we use the TLSA used in Brunton et al. (Reference Brunton, Proctor and Kutz2016a) and the Alasso (Zou Reference Zou2006) to obtain the coefficient matrix ![]() $\varXi$ following our preliminary tests. Details can be found in the Appendices.
$\varXi$ following our preliminary tests. Details can be found in the Appendices.
2.2. CNN-AE
We use a CNN (LeCun et al. Reference LeCun, Bottou, Bengio and Haffner1998) AE (Hinton & Salakhutdinov Reference Hinton and Salakhutdinov2006) for order reduction of high-dimensional data, as shown in figure 2. As an example, we show the CNN-AE with three hidden layers. In a training process, the AE ![]() ${\mathcal {F}}$ is trained to output the same data as the input data
${\mathcal {F}}$ is trained to output the same data as the input data ![]() $\boldsymbol q$ such that
$\boldsymbol q$ such that ![]() ${\boldsymbol q}\approx {{\mathcal {F}}}({\boldsymbol q};{\boldsymbol w})$, where
${\boldsymbol q}\approx {{\mathcal {F}}}({\boldsymbol q};{\boldsymbol w})$, where ![]() ${\boldsymbol w}$ denotes the weights of the machine learning model. The process to optimize the weights
${\boldsymbol w}$ denotes the weights of the machine learning model. The process to optimize the weights ![]() $\boldsymbol w$ can be formulated as an iterative minimization of an error function
$\boldsymbol w$ can be formulated as an iterative minimization of an error function ![]() $E$,
$E$,
For the use of the AE as a dimension compressor, the dimension of an intermediate space called the latent space ![]() $\boldsymbol \eta$ is smaller than that of the input or output data
$\boldsymbol \eta$ is smaller than that of the input or output data ![]() $\boldsymbol q$ as illustrated in figure 2. When we are able to obtain the output
$\boldsymbol q$ as illustrated in figure 2. When we are able to obtain the output ![]() ${{\mathcal {F}}}(\boldsymbol q)$ similar to the input
${{\mathcal {F}}}(\boldsymbol q)$ similar to the input ![]() $\boldsymbol q$ such that
$\boldsymbol q$ such that ![]() ${\boldsymbol q}\approx {{\mathcal {F}}}({\boldsymbol q})$, it can be guaranteed that the latent vector
${\boldsymbol q}\approx {{\mathcal {F}}}({\boldsymbol q})$, it can be guaranteed that the latent vector ![]() $\boldsymbol r$ is a low-dimensional representation of its input or output
$\boldsymbol r$ is a low-dimensional representation of its input or output ![]() $\boldsymbol q$. In an AE, the dimension compressor is called the encoder
$\boldsymbol q$. In an AE, the dimension compressor is called the encoder ![]() ${{\mathcal {F}}}_e$ (the left-hand part in figure 2) and the counterpart is referred to as the decoder
${{\mathcal {F}}}_e$ (the left-hand part in figure 2) and the counterpart is referred to as the decoder ![]() ${{\mathcal {F}}}_d$ (the right-hand part in figure 2). Using them, the internal procedure of the AE can be expressed as
${{\mathcal {F}}}_d$ (the right-hand part in figure 2). Using them, the internal procedure of the AE can be expressed as
In the present study, the dimension of the latent space for the problems of a cylinder wake and its transient process is set to two following our previous work (Murata, Fukami & Fukagata Reference Murata, Fukami and Fukagata2020). Murata et al. (Reference Murata, Fukami and Fukagata2020) reported that the flow fields can be mapped into a low-dimensional latent space successfully while keeping the information of high-dimensional flow fields. For the example of a two-parallel cylinder wake in § 3.3, the dimension of the latent space is set to four to handle its quasi-periodicity, accordingly. For construction of the AE, the ![]() $L_2$ norm error is applied as the error function
$L_2$ norm error is applied as the error function ![]() $E$ and the Adam optimizer (Kingma & Ba Reference Kingma and Ba2014) is utilized for updating the weights in the iterative training process.
$E$ and the Adam optimizer (Kingma & Ba Reference Kingma and Ba2014) is utilized for updating the weights in the iterative training process.
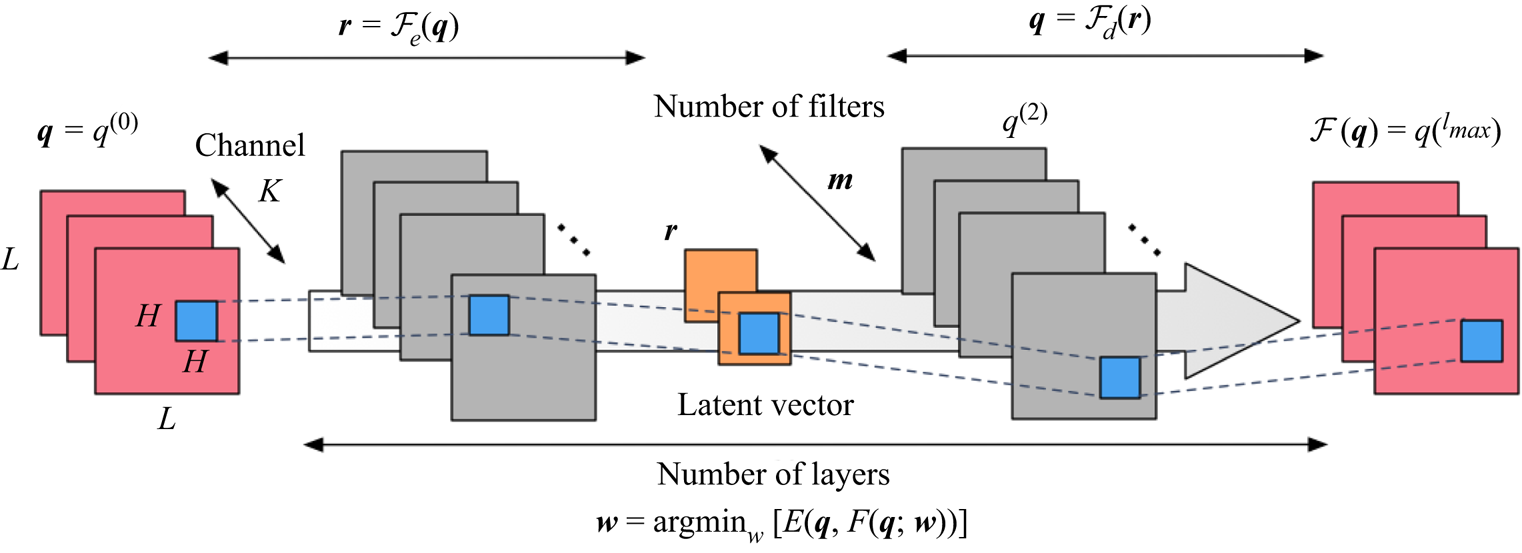
Figure 2. Convolutional neural network-based autoencoder.
Next, let us briefly explain the convolutional neural network. In the scheme of the convolutional neural network, a filter ![]() $h$, whose size is
$h$, whose size is ![]() $H\times H,$ is utilized as the weights
$H\times H,$ is utilized as the weights ![]() $\boldsymbol w$, as shown in figure 3
$\boldsymbol w$, as shown in figure 3![]() $(a)$. The mathematical expression here is
$(a)$. The mathematical expression here is
 \begin{equation} q^{(l)}_{ijm} = {\psi}\left(\sum^{K-1}_{k=0}\sum^{H-1}_{p=0}\sum^{H-1}_{s=0}h_{p{s}km}^{(l)} q_{i+p-C,j+{s-C},k}^{(l-1)} + b^{(l)}_{ijm}\right), \end{equation}
\begin{equation} q^{(l)}_{ijm} = {\psi}\left(\sum^{K-1}_{k=0}\sum^{H-1}_{p=0}\sum^{H-1}_{s=0}h_{p{s}km}^{(l)} q_{i+p-C,j+{s-C},k}^{(l-1)} + b^{(l)}_{ijm}\right), \end{equation}
where ![]() $C=\textrm {floor}(H/2)$,
$C=\textrm {floor}(H/2)$, ![]() $q^{(l)}$ is the output at layer
$q^{(l)}$ is the output at layer ![]() $l$, and
$l$, and ![]() $K$ is the number of variables in the data (e.g.
$K$ is the number of variables in the data (e.g. ![]() $K=1$ for black-and-white photos and
$K=1$ for black-and-white photos and ![]() $K=3$ for RGB images). Although not shown in figure 3,
$K=3$ for RGB images). Although not shown in figure 3, ![]() $b$ is a bias added to the results of the filter operation. The activation function
$b$ is a bias added to the results of the filter operation. The activation function ![]() $\psi$ is usually a monotonically increasing nonlinear function. The AE can achieve more effective dimension reduction than the linear theory-based method, i.e. POD (Lumley Reference Lumley1967), thanks to the nonlinear activation function (Milano & Koumoutsakos Reference Milano and Koumoutsakos2002; Fukami et al. Reference Fukami, Hasegawa, Nakamura, Morimoto and Fukagata2020b; Murata et al. Reference Murata, Fukami and Fukagata2020). In the present study, a hyperbolic tangent function
$\psi$ is usually a monotonically increasing nonlinear function. The AE can achieve more effective dimension reduction than the linear theory-based method, i.e. POD (Lumley Reference Lumley1967), thanks to the nonlinear activation function (Milano & Koumoutsakos Reference Milano and Koumoutsakos2002; Fukami et al. Reference Fukami, Hasegawa, Nakamura, Morimoto and Fukagata2020b; Murata et al. Reference Murata, Fukami and Fukagata2020). In the present study, a hyperbolic tangent function ![]() $\psi (a)=(e^{a}-e^{-a})\cdot (e^{a}+e^{-a})^{-1}$ is adopted for the activation function following Murata et al. (Reference Murata, Fukami and Fukagata2020). Moreover, we use the convolutional neural network to construct the AE because the CNN is good at handling high-dimensional data with lower computational costs than fully connected models, i.e. multilayer perceptron, thanks to the filter concept which assumes that pixels of images have no strong relationship with those of far areas. Recently, the use of CNN has emerged to deal with high-dimensional problems including fluid dynamics (Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2019a,Reference Fukami, Fukagata and Tairab; Fukami et al. Reference Fukami, Nabae, Kawai and Fukagata2019c; Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2020a; Fukami et al. Reference Fukami, Maulik, Ramachandra, Fukagata and Taira2021b; Omata & Shirayama Reference Omata and Shirayama2019; Morimoto, Fukami & Fukagata Reference Morimoto, Fukami and Fukagata2020a; Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2021a; Matsuo et al. Reference Matsuo, Nakamura, Morimoto, Fukami and Fukagata2021; Morimoto et al. Reference Morimoto, Fukami, Zhang, Nair and Fukagata2021), although this concept was originally developed in the field of computer science.
$\psi (a)=(e^{a}-e^{-a})\cdot (e^{a}+e^{-a})^{-1}$ is adopted for the activation function following Murata et al. (Reference Murata, Fukami and Fukagata2020). Moreover, we use the convolutional neural network to construct the AE because the CNN is good at handling high-dimensional data with lower computational costs than fully connected models, i.e. multilayer perceptron, thanks to the filter concept which assumes that pixels of images have no strong relationship with those of far areas. Recently, the use of CNN has emerged to deal with high-dimensional problems including fluid dynamics (Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2019a,Reference Fukami, Fukagata and Tairab; Fukami et al. Reference Fukami, Nabae, Kawai and Fukagata2019c; Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2020a; Fukami et al. Reference Fukami, Maulik, Ramachandra, Fukagata and Taira2021b; Omata & Shirayama Reference Omata and Shirayama2019; Morimoto, Fukami & Fukagata Reference Morimoto, Fukami and Fukagata2020a; Fukami, Fukagata & Taira Reference Fukami, Fukagata and Taira2021a; Matsuo et al. Reference Matsuo, Nakamura, Morimoto, Fukami and Fukagata2021; Morimoto et al. Reference Morimoto, Fukami, Zhang, Nair and Fukagata2021), although this concept was originally developed in the field of computer science.
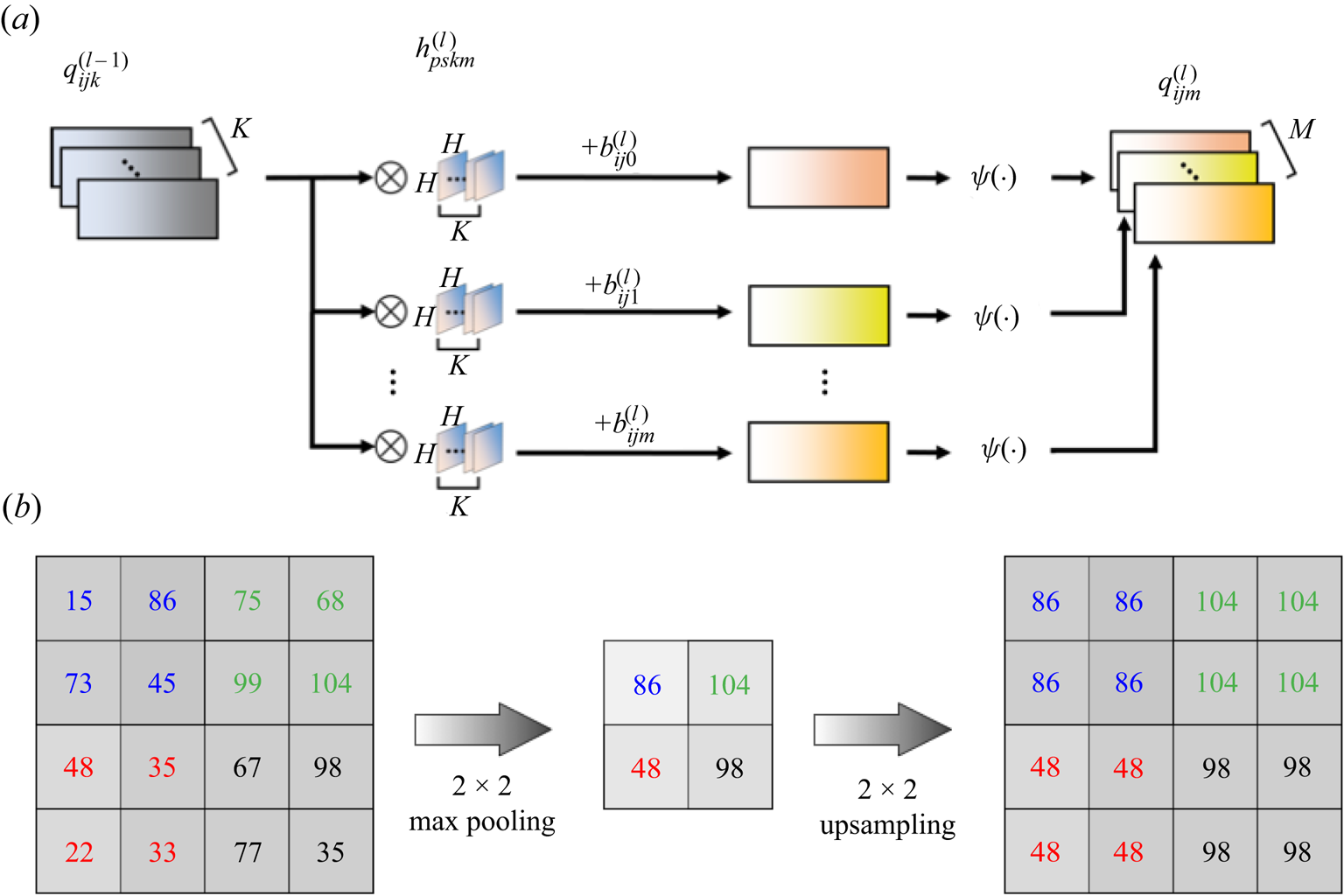
Figure 3. Internal procedure of convolutional neural network: ![]() $(a)$ filter operation with activation function and
$(a)$ filter operation with activation function and ![]() $(b)$ maximum pooling and upsampling.
$(b)$ maximum pooling and upsampling.
2.3. The CNN-SINDy-based ROM
By combining the CNN-AE and SINDy, we present the machine-learning-based ROM (ML-ROM) as shown in figure 4. The CNN-AE first works to map a high-dimensional flow field into low-dimensional latent space. The SINDy is then performed to obtain a governing equation of the mapped low-dimensional latent vector. Unifying the predicted latent vector by the SINDy with the CNN decoder, we can obtain the temporal evolution of high-dimensional flow field as presented in figure 4. Moreover, the issue with high-dimensional variables and SINDy can also be avoided. Note again that the present ROM is inspired by Hasegawa et al. (Reference Hasegawa, Fukami, Murata and Fukagata2019, Reference Hasegawa, Fukami, Murata and Fukagata2020a,Reference Hasegawa, Fukami, Murata and Fukagatab) who capitalized on a long short-term memory instead of SINDy. We apply this framework to a two-dimensional cylinder wake in § 3.1, its transient process in § 3.2 and a wake of two-parallel cylinders in § 3.3. In this study, we perform a fivefold cross-validation (Brunton & Kutz Reference Brunton and Kutz2019) to create all machine learning models, although only the results of a single case will be presented, for brevity. The sample code for the present reduced-order model is available from https://github.com/kfukami/CNN-SINDy-MLROM.
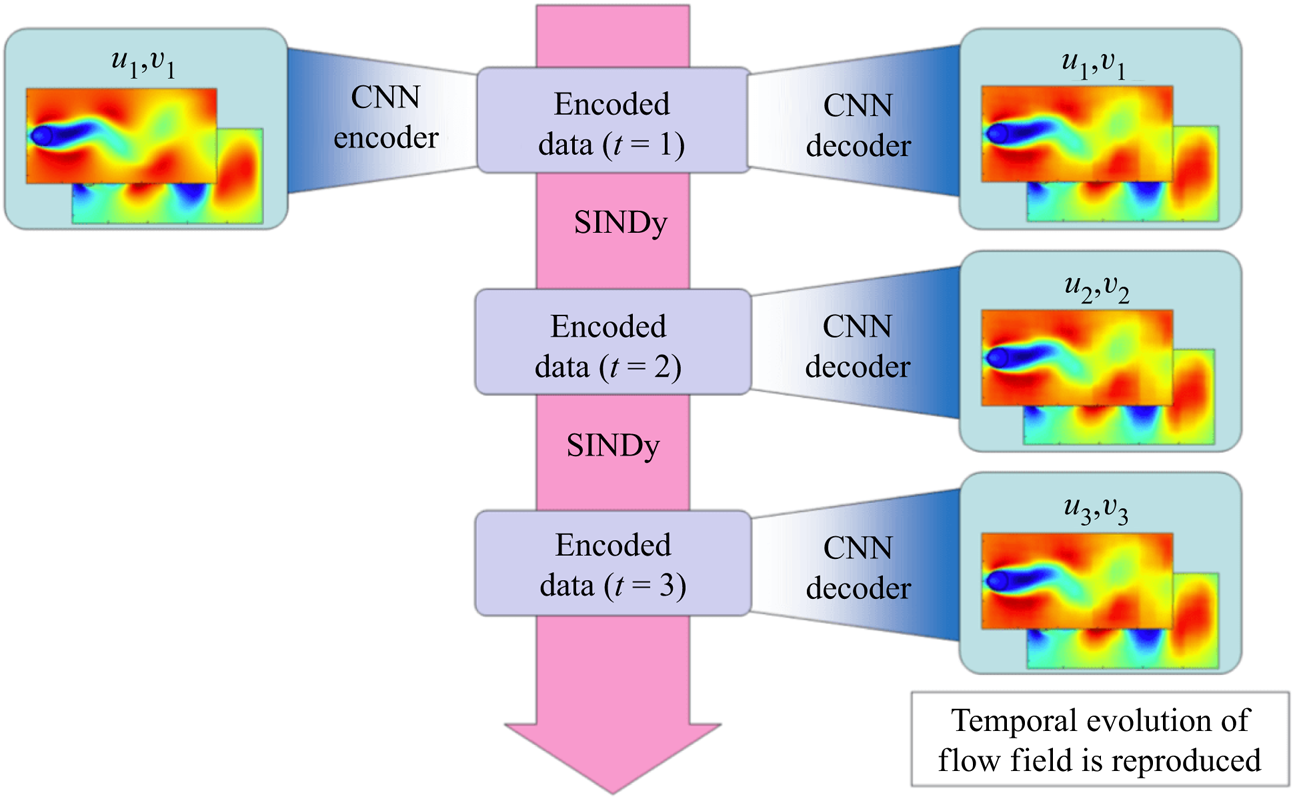
Figure 4. The CNN-SINDy-based ROM for fluid flows.
3. Results and discussion
3.1. Example 1: periodic cylinder wake
Here, let us consider a two-dimensional cylinder wake using a two-dimensional direct numerical simulation (DNS). The governing equations are the incompressible continuity and Navier–Stokes equations,
where ![]() $\boldsymbol {u}$ and
$\boldsymbol {u}$ and ![]() $p$ represent the velocity vector and pressure, respectively. All quantities are made dimensionless by the fluid density, the free stream velocity and the cylinder diameter. The Reynolds number based on the cylinder diameter is
$p$ represent the velocity vector and pressure, respectively. All quantities are made dimensionless by the fluid density, the free stream velocity and the cylinder diameter. The Reynolds number based on the cylinder diameter is ![]() $Re _D=100$. The size of the computational domain is
$Re _D=100$. The size of the computational domain is ![]() $L_x=25.6$ and
$L_x=25.6$ and ![]() $L_y=20.0$ in the streamwise (
$L_y=20.0$ in the streamwise (![]() $x$) and the transverse (
$x$) and the transverse (![]() $y$) directions, respectively. The origin of coordinates is defined at the centre of the inflow boundary. A Cartesian grid with the uniform grid spacing of
$y$) directions, respectively. The origin of coordinates is defined at the centre of the inflow boundary. A Cartesian grid with the uniform grid spacing of ![]() $\Delta x=\Delta y = 0.025$ is used; thus, the number of grid points is
$\Delta x=\Delta y = 0.025$ is used; thus, the number of grid points is ![]() $(N_x, N_y)=(1024, 800)$. We use the ghost cell method (Kor, Badri Ghomizad & Fukagata Reference Kor, Badri Ghomizad and Fukagata2017) to impose the no-slip boundary condition on the surface of cylinder whose centre is located at
$(N_x, N_y)=(1024, 800)$. We use the ghost cell method (Kor, Badri Ghomizad & Fukagata Reference Kor, Badri Ghomizad and Fukagata2017) to impose the no-slip boundary condition on the surface of cylinder whose centre is located at ![]() $(x,y)=(9,0)$. In the present study, we utilize the flows around the cylinder as the training data set, i.e.
$(x,y)=(9,0)$. In the present study, we utilize the flows around the cylinder as the training data set, i.e. ![]() $8.2 \leq x \leq 17.8$ and
$8.2 \leq x \leq 17.8$ and ![]() $-2.4 \leq y \leq 2.4$ with
$-2.4 \leq y \leq 2.4$ with ![]() $(N_x^{*}, N_y^{*})=(384, 192)$. The fluctuation components of streamwise velocity
$(N_x^{*}, N_y^{*})=(384, 192)$. The fluctuation components of streamwise velocity ![]() $u$ and transverse velocity
$u$ and transverse velocity ![]() $v$ are considered as the input and output attributes for CNN-AE. The time interval of the flow field data is
$v$ are considered as the input and output attributes for CNN-AE. The time interval of the flow field data is ![]() $\Delta t = 0.025$ corresponding to approximately 230 snapshots per a period with the Strouhal number
$\Delta t = 0.025$ corresponding to approximately 230 snapshots per a period with the Strouhal number ![]() $St=0.172$.
$St=0.172$.
As mentioned above, the SINDy is employed to identify the ordinary differential equations that govern the temporal evolution of the mapped vector obtained by the CNN encoder. The time history and the trajectory of the mapped latent vector ![]() ${\boldsymbol r}=(r_1,r_2)$ are shown in figure 5. For the assessment of the candidate models, we integrate the differential equations to reproduce the time history. Note in passing that the indices based on the
${\boldsymbol r}=(r_1,r_2)$ are shown in figure 5. For the assessment of the candidate models, we integrate the differential equations to reproduce the time history. Note in passing that the indices based on the ![]() $L_2$ error are not suitable since the slight difference between the period of reproduced oscillation and that of original one results in large
$L_2$ error are not suitable since the slight difference between the period of reproduced oscillation and that of original one results in large ![]() $L_2$ errors for oscillating systems. We here use the amplitude and the frequency of oscillation to evaluate the similarity between the reproduced waveform and the original one. Hereafter, the error rate of the amplitude and the frequency are shown in the figures below for simplicity. The number of terms is also considered for the parsimonious model selection.
$L_2$ errors for oscillating systems. We here use the amplitude and the frequency of oscillation to evaluate the similarity between the reproduced waveform and the original one. Hereafter, the error rate of the amplitude and the frequency are shown in the figures below for simplicity. The number of terms is also considered for the parsimonious model selection.

Figure 5. Latent vector dynamics of a periodic shedding case: ![]() $(a)$ time history and
$(a)$ time history and ![]() $(b)$ trajectory.
$(b)$ trajectory.
We consider two regression methods for SINDy, i.e. TLSA and Alasso, following our previous tests. Let us present the results of parameter search utilizing TLSA in figure 6. Note here that we use 10 000 mapped vectors for the construction of a SINDy model. Using ![]() $\alpha =1$, the reproduced trajectory is in excellent agreement with the original one. However, there are many terms in the ordinary differential equations and some coefficients are too large, although the oscillation are presented with a shallow range (
$\alpha =1$, the reproduced trajectory is in excellent agreement with the original one. However, there are many terms in the ordinary differential equations and some coefficients are too large, although the oscillation are presented with a shallow range (![]() $-1, 1$). The result with the TLSA here is likely because we do not use the data processing, which causes the large regression coefficients and non-sparse results. On the other hand, the reproduced trajectory with
$-1, 1$). The result with the TLSA here is likely because we do not use the data processing, which causes the large regression coefficients and non-sparse results. On the other hand, the reproduced trajectory with ![]() $\alpha =10$ converges to a point around
$\alpha =10$ converges to a point around ![]() $(r_1,r_2)=(0.6,0)$, although the model becomes parsimonious. Since the predicted latent vector converges after
$(r_1,r_2)=(0.6,0)$, although the model becomes parsimonious. Since the predicted latent vector converges after ![]() $t\approx 4$ as shown in the time history of figure 6, the temporal evolution of the flow field by the CNN decoder is also frozen, as shown in figure 7. Other observation here is that there remains no terms in the ordinary differential equations with high threshold, i.e.
$t\approx 4$ as shown in the time history of figure 6, the temporal evolution of the flow field by the CNN decoder is also frozen, as shown in figure 7. Other observation here is that there remains no terms in the ordinary differential equations with high threshold, i.e. ![]() $\alpha \geq 50$.
$\alpha \geq 50$.
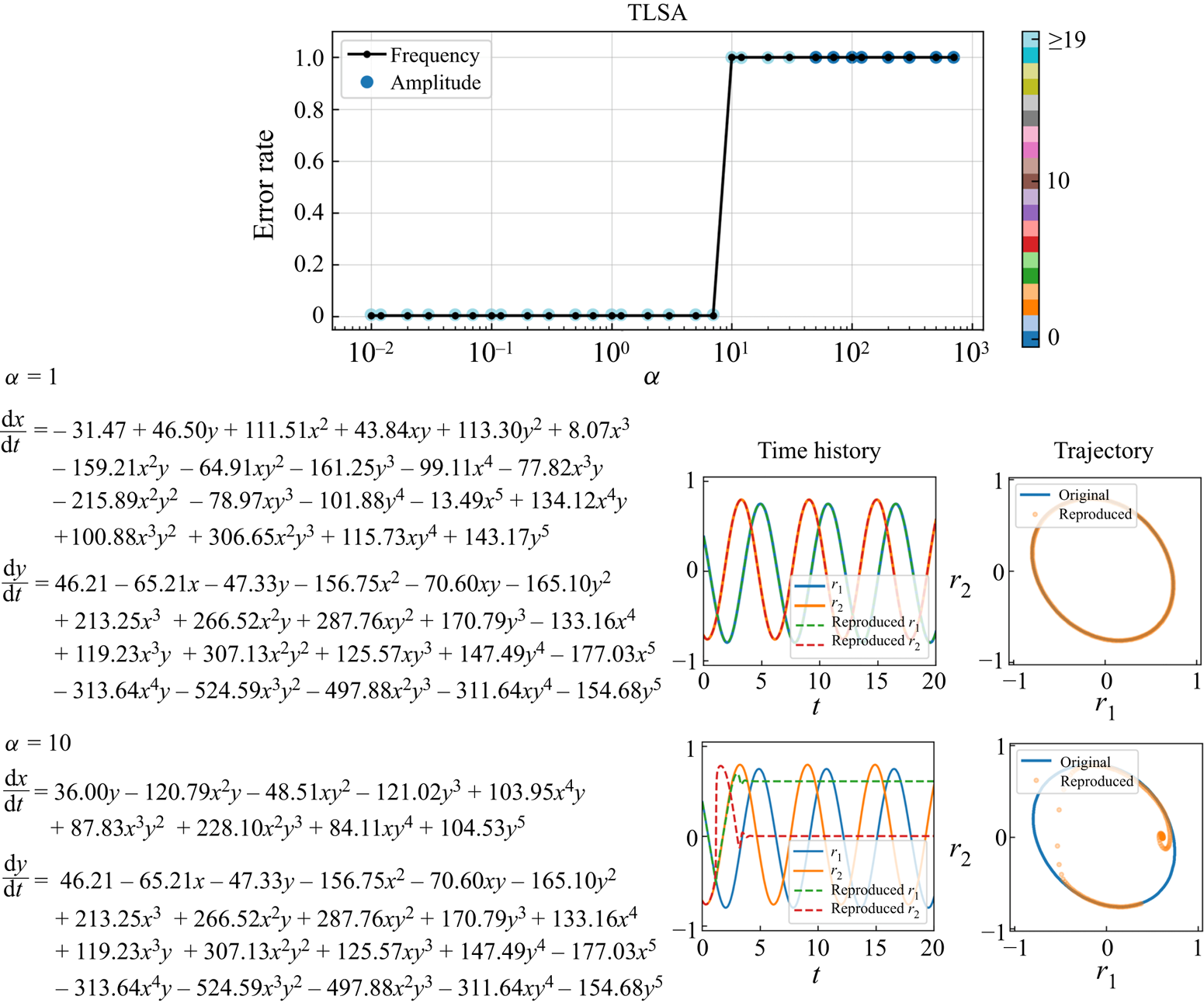
Figure 6. Results with TLSA for the periodic cylinder example. Parameter search results, examples of obtained equations, and reproduced trajectories with ![]() $\alpha =1$ and
$\alpha =1$ and ![]() $\alpha =10$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components
$\alpha =10$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components ![]() $(r_1, r_2)$ are represented by
$(r_1, r_2)$ are represented by ![]() $(x,y)$ for clarity.
$(x,y)$ for clarity.

Figure 7. Temporally evolved flow fields of DNS and the reproduced flow field with ![]() $\alpha =1$ and
$\alpha =1$ and ![]() $\alpha =10$. With
$\alpha =10$. With ![]() $\alpha =10$, the flow field is frozen after around
$\alpha =10$, the flow field is frozen after around ![]() $t=4$ (enhanced using blue colour).
$t=4$ (enhanced using blue colour).
With Alasso as the regression method, we can find the candidate models with low errors at ![]() $\alpha =2 \times 10^{-5}$ and
$\alpha =2 \times 10^{-5}$ and ![]() $1 \times 10^{-4}$, as shown in figure 8. At
$1 \times 10^{-4}$, as shown in figure 8. At ![]() $\alpha =2 \times 10^{-5}$, the ordinary differential equations consist of four coefficients in total and the reproduced trajectory gradually converges as shown. On the other hand, by choosing the appropriate sparsity constant, i.e.
$\alpha =2 \times 10^{-5}$, the ordinary differential equations consist of four coefficients in total and the reproduced trajectory gradually converges as shown. On the other hand, by choosing the appropriate sparsity constant, i.e. ![]() $\alpha = 1 \times 10^{-4}$, the circle-like oscillating trajectory, which is similar to the reference, can be represented with only two terms. We then check the reproduced flow field by the combination of the predicted latent vector by SINDy and CNN decoder, as shown in figure 9. The temporal evolution of high-dimensional dynamics can be reproduced well using the proposed model, although the period of the two fields are slightly different.
$\alpha = 1 \times 10^{-4}$, the circle-like oscillating trajectory, which is similar to the reference, can be represented with only two terms. We then check the reproduced flow field by the combination of the predicted latent vector by SINDy and CNN decoder, as shown in figure 9. The temporal evolution of high-dimensional dynamics can be reproduced well using the proposed model, although the period of the two fields are slightly different.
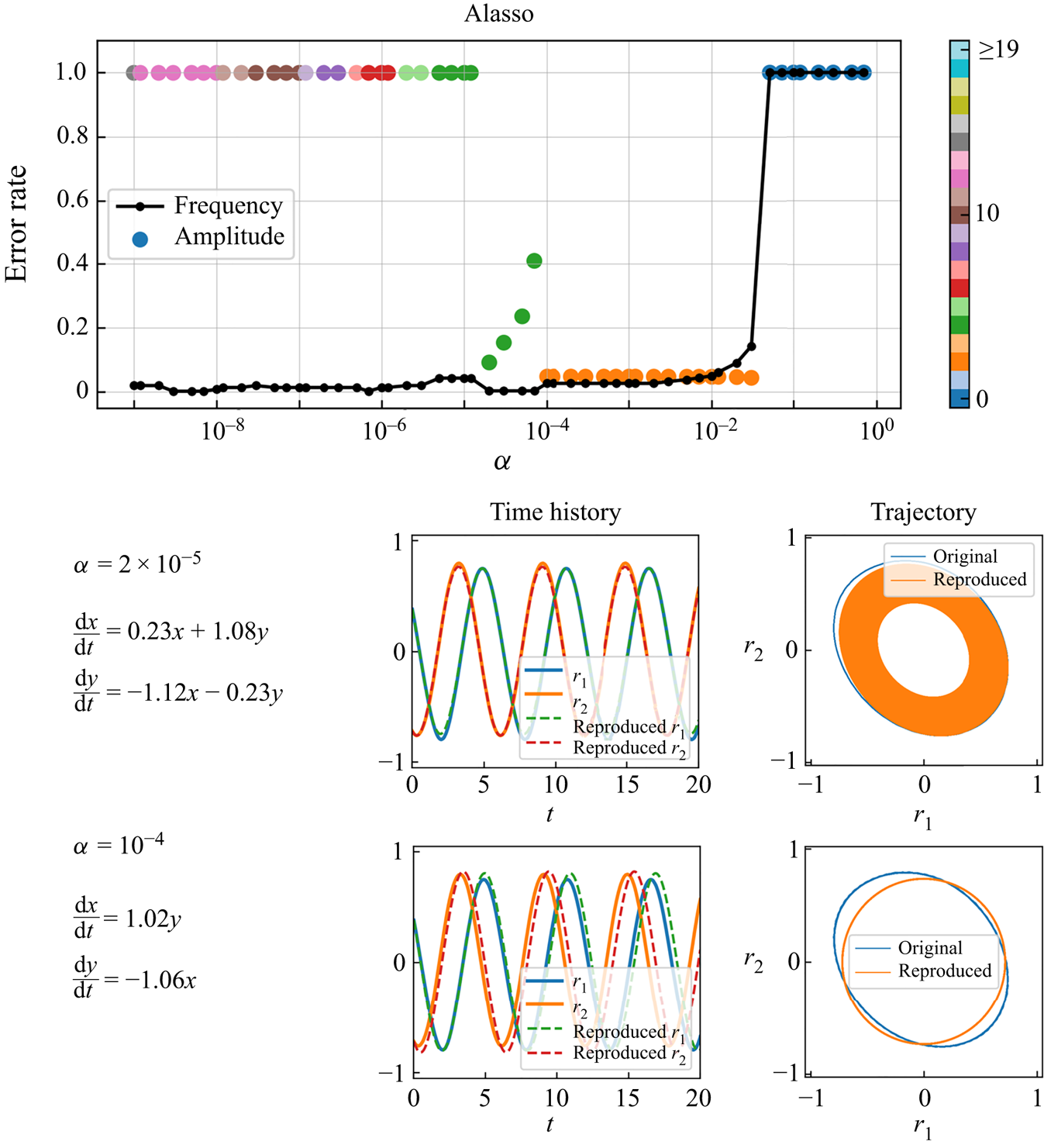
Figure 8. Results with Alasso of a periodic cylinder example. Parameter search results, examples of obtained equations, and reproduced trajectories with ![]() $\alpha =2 \times 10^{-5}$ and
$\alpha =2 \times 10^{-5}$ and ![]() $\alpha =1 \times 10^{-4}$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components
$\alpha =1 \times 10^{-4}$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components ![]() $(r_1, r_2)$ are represented by
$(r_1, r_2)$ are represented by ![]() $(x,y)$ for clarity.
$(x,y)$ for clarity.

Figure 9. Time history of the latent vector and temporal evolution of the wake of DNS and the reproduced field at ![]() $(a)$
$(a)$ ![]() $t=1025$,
$t=1025$, ![]() $(b)$
$(b)$ ![]() $t=1026$,
$t=1026$, ![]() $(c)$
$(c)$ ![]() $t=1027$ and
$t=1027$ and ![]() $(d)$
$(d)$ ![]() $t=1028$.
$t=1028$.
The quantitative analysis with the probability density function, the mean streamwise velocity at ![]() $y=0$, and the time history of ERR is summarized in figure 10. The ERR
$y=0$, and the time history of ERR is summarized in figure 10. The ERR ![]() ${\mathcal {R}}$ is defined as
${\mathcal {R}}$ is defined as
 \begin{equation} {\mathcal{R}}= \dfrac{ \int_S (u^{\prime 2}_{ Rep}+{v^{\prime}}^{2}_{ Rep})\,\textrm{d}S }{ \int_S (u^{\prime 2}_{ DNS}+v^{\prime 2}_{ DNS}) \,\textrm{d}S }, \end{equation}
\begin{equation} {\mathcal{R}}= \dfrac{ \int_S (u^{\prime 2}_{ Rep}+{v^{\prime}}^{2}_{ Rep})\,\textrm{d}S }{ \int_S (u^{\prime 2}_{ DNS}+v^{\prime 2}_{ DNS}) \,\textrm{d}S }, \end{equation}
where ![]() $(u'_{ Rep},v'_{ Rep})$ and
$(u'_{ Rep},v'_{ Rep})$ and ![]() $(u'_{ DNS}, v'_{ DNS}$) denote the fluctuation components of the reproduced velocity and the original velocity, respectively. For the probability density function, the distribution of the CNN-SINDy model is in excellent agreement with the reference DNS data. Since the SINDy model of the present case integrates the latent vector via the CNN-AE which can map a high-dimensional flow field into low-dimensional space efficiently thanks to the nonlinear activation function (Murata et al. Reference Murata, Fukami and Fukagata2020), the SINDy outperforms POD with two modes as long as the appropriate waveforms can be obtained. In other words, the obtained equation can be integrated stably. The success of the CNN-SINDy-based modelling can be also seen with time-averaged velocity and energy containing rate in figure 10.
$(u'_{ DNS}, v'_{ DNS}$) denote the fluctuation components of the reproduced velocity and the original velocity, respectively. For the probability density function, the distribution of the CNN-SINDy model is in excellent agreement with the reference DNS data. Since the SINDy model of the present case integrates the latent vector via the CNN-AE which can map a high-dimensional flow field into low-dimensional space efficiently thanks to the nonlinear activation function (Murata et al. Reference Murata, Fukami and Fukagata2020), the SINDy outperforms POD with two modes as long as the appropriate waveforms can be obtained. In other words, the obtained equation can be integrated stably. The success of the CNN-SINDy-based modelling can be also seen with time-averaged velocity and energy containing rate in figure 10.
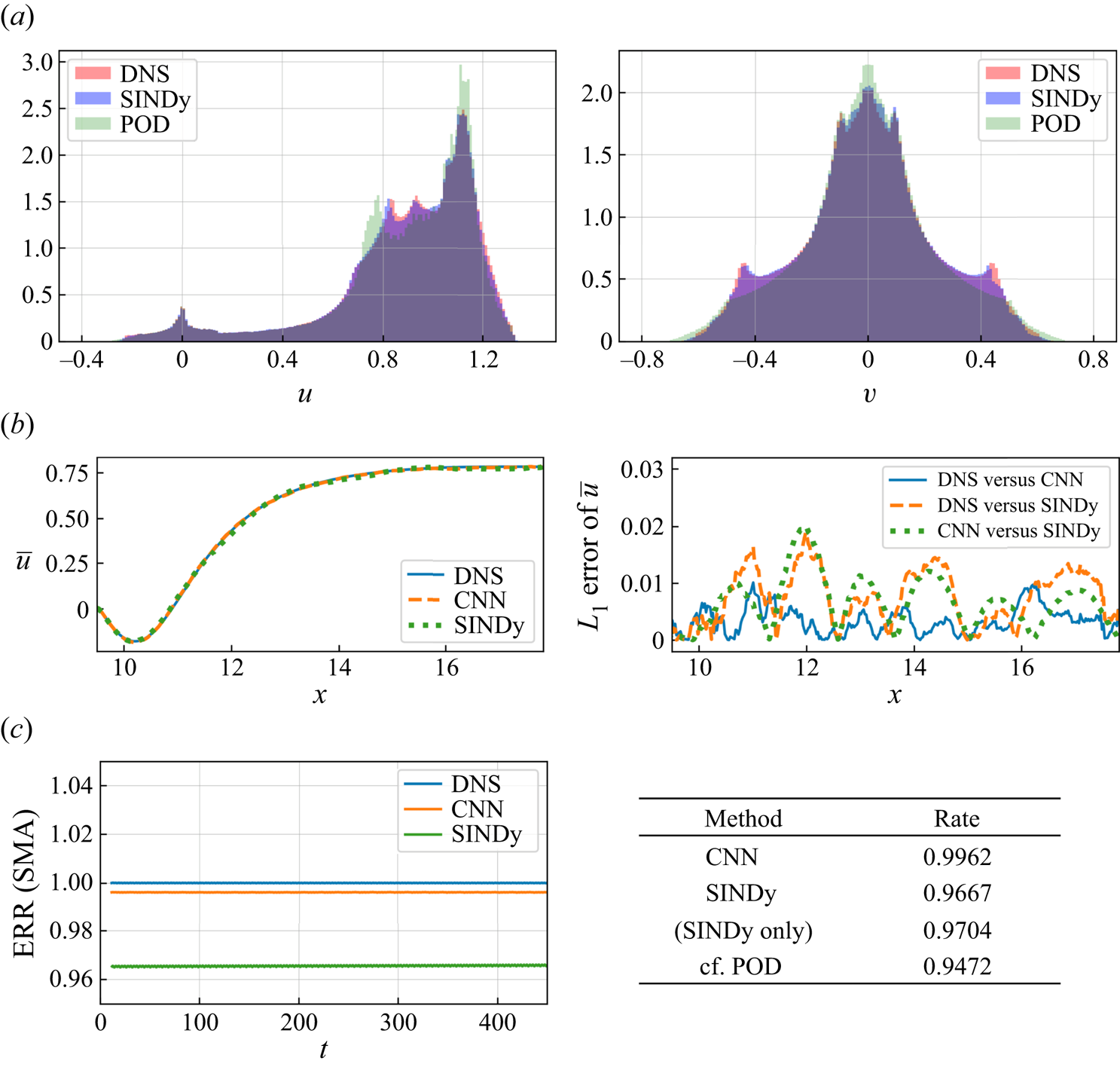
Figure 10. Evaluation of reproduced flow field with a periodic shedding. ![]() $(a)$ Probability density function,
$(a)$ Probability density function, ![]() $(b)$ mean streamwise velocity at
$(b)$ mean streamwise velocity at ![]() $y=0$ and
$y=0$ and ![]() $(c)$ the energy reconstruction rate (ERR). Simple moving average (SMA) of ERR is shown here for the clearness.
$(c)$ the energy reconstruction rate (ERR). Simple moving average (SMA) of ERR is shown here for the clearness.
3.2. Example 2: transient wake of cylinder flow
As the second example for the combination of CNN and SINDy, we consider the transient process of a flow around a circular cylinder at ![]() ${Re}_D=100$. For taking into account the transient process, the streamwise length of the computational domain and that of the flow field data are extended to
${Re}_D=100$. For taking into account the transient process, the streamwise length of the computational domain and that of the flow field data are extended to ![]() $L_x=51.2$ and
$L_x=51.2$ and ![]() $8.2 \leq x \leq 37$, i.e.
$8.2 \leq x \leq 37$, i.e. ![]() $N_x^{*}=1152$, same set-up with Murata et al. (Reference Murata, Fukami and Fukagata2020). The time history and the trajectory in the latent space are shown in figure 11. Since the trajectory looks like a circle as shown in figure 11
$N_x^{*}=1152$, same set-up with Murata et al. (Reference Murata, Fukami and Fukagata2020). The time history and the trajectory in the latent space are shown in figure 11. Since the trajectory looks like a circle as shown in figure 11![]() $(b)$, we use the residual sum of error of
$(b)$, we use the residual sum of error of ![]() $r_1^{2}+r_2^{2}$ between the original value and the reproduced value as the evaluation index in this example.
$r_1^{2}+r_2^{2}$ between the original value and the reproduced value as the evaluation index in this example.
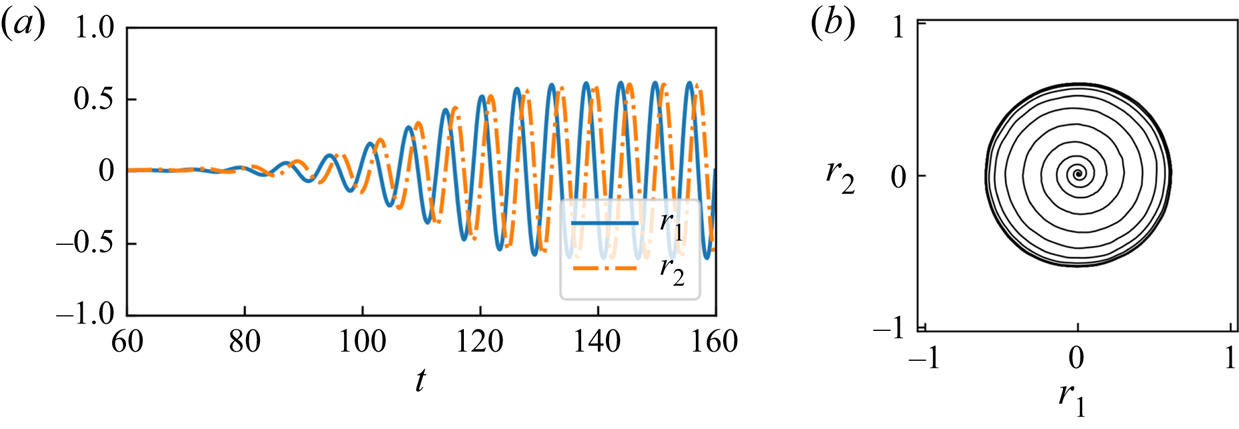
Figure 11. Latent vector dynamics of the transient process: (![]() $a$) time history and (
$a$) time history and (![]() $b$) trajectory.
$b$) trajectory.
For SINDy, we use the data with ![]() $t=[60,160]$. The library matrix contains up to fifth-order terms. Although equations, which can provide the correct temporal evolution of the latent vector, can be obtained with Alasso by including higher-order terms, the model here is, of course, not sparse and so difficult to interpret.
$t=[60,160]$. The library matrix contains up to fifth-order terms. Although equations, which can provide the correct temporal evolution of the latent vector, can be obtained with Alasso by including higher-order terms, the model here is, of course, not sparse and so difficult to interpret.
The parameter search results with TLSA for transient wake are summarized in figure 12. Since the trajectory here is simple as shown, we can obtain the governing equations, which provide the reasonable agreement with the reference, at ![]() $\alpha =7\times 10^{-2}$. With a higher sparsity constant, i.e.
$\alpha =7\times 10^{-2}$. With a higher sparsity constant, i.e. ![]() $\alpha =0.7$, the equation provides a temporal evolution of the latent vector with almost no oscillation.
$\alpha =0.7$, the equation provides a temporal evolution of the latent vector with almost no oscillation.

Figure 12. Results with TLSA of the transient example. Parameter search results, examples of obtained equations, and reproduced trajectories with ![]() $\alpha =7 \times 10^{-2}$ and
$\alpha =7 \times 10^{-2}$ and ![]() $\alpha =0.7$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components
$\alpha =0.7$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components ![]() $(r_1, r_2)$ are represented by
$(r_1, r_2)$ are represented by ![]() $(x,y)$ for clarity.
$(x,y)$ for clarity.
Alasso is also considered, as shown in figure 13. Although the number of terms is larger than that in the periodic shedding example, the trajectory can be reproduced successfully at ![]() $\alpha =1.2 \times 10^{-8}$. With a higher sparsity constant, e.g.
$\alpha =1.2 \times 10^{-8}$. With a higher sparsity constant, e.g. ![]() $\alpha =1.2 \times 10^{-2}$, the developing oscillation is not reproduced due to a lack of number of terms. Noteworthy here is that the error for frequency is almost negligible in the range of
$\alpha =1.2 \times 10^{-2}$, the developing oscillation is not reproduced due to a lack of number of terms. Noteworthy here is that the error for frequency is almost negligible in the range of ![]() $5\times 10^{-6}\leq \alpha \leq 10^{-3}$ in spite of the high error rate regarding
$5\times 10^{-6}\leq \alpha \leq 10^{-3}$ in spite of the high error rate regarding ![]() $x^{2}+y^{2}$. This is because the slight oscillation occurs with a similar frequency to the solution. Although the identified equation here is more complex than the well known transient system with a two-dimensional paraboloic manifold (Sipp & Lebedev Reference Sipp and Lebedev2007; Loiseau & Brunton Reference Loiseau and Brunton2018; Loiseau, Brunton & Noack Reference Loiseau, Brunton and Noack2018a), it is likely caused by the complexity of captured information inside the AE modes compared with the POD modes (Murata et al. Reference Murata, Fukami and Fukagata2020). This observation enables us to notice the trade-off relationship between the used information associated with the number of modes and the sparsity of equation. Hence, taking a constraint for nonlinear AE modes to be useful, e.g. orthogonal, may be helpful in identifying more sparse dynamics (Champion et al. Reference Champion, Lusch, Kutz and Brunton2019a; Ladjal, Newson & Pham Reference Ladjal, Newson and Pham2019; Jayaraman & Mamun Reference Jayaraman and Mamun2020).
$x^{2}+y^{2}$. This is because the slight oscillation occurs with a similar frequency to the solution. Although the identified equation here is more complex than the well known transient system with a two-dimensional paraboloic manifold (Sipp & Lebedev Reference Sipp and Lebedev2007; Loiseau & Brunton Reference Loiseau and Brunton2018; Loiseau, Brunton & Noack Reference Loiseau, Brunton and Noack2018a), it is likely caused by the complexity of captured information inside the AE modes compared with the POD modes (Murata et al. Reference Murata, Fukami and Fukagata2020). This observation enables us to notice the trade-off relationship between the used information associated with the number of modes and the sparsity of equation. Hence, taking a constraint for nonlinear AE modes to be useful, e.g. orthogonal, may be helpful in identifying more sparse dynamics (Champion et al. Reference Champion, Lusch, Kutz and Brunton2019a; Ladjal, Newson & Pham Reference Ladjal, Newson and Pham2019; Jayaraman & Mamun Reference Jayaraman and Mamun2020).

Figure 13. Results with Alasso of the transient example. Parameter search results, examples of obtained equations, and reproduced trajectories with ![]() $\alpha =1.2 \times 10^{-8}$ and
$\alpha =1.2 \times 10^{-8}$ and ![]() $\alpha =1.2 \times 10^{-2}$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components
$\alpha =1.2 \times 10^{-2}$ are shown. Colour of amplitude plot indicates the total number of terms. In the ordinary differential equations, the latent vector components ![]() $(r_1, r_2)$ are represented by
$(r_1, r_2)$ are represented by ![]() $(x,y)$ for clarity.
$(x,y)$ for clarity.
The streamwise velocity fields reproduced by the CNN-AE and the integrated latent variables with the Alasso-based SINDy are presented in figure 14. The present two sparsity constants here correspond to the results in figure 13. With ![]() $\alpha =1.2\times 10^{-8}$, the flow field can successfully be reproduced thanks to nonlinear terms in the identified equations by SINDy. In contrast, it is tough to capture the transient behaviour correctly by the CNN-SINDy model with
$\alpha =1.2\times 10^{-8}$, the flow field can successfully be reproduced thanks to nonlinear terms in the identified equations by SINDy. In contrast, it is tough to capture the transient behaviour correctly by the CNN-SINDy model with ![]() $\alpha =1.2\times 10^{-2}$, which can explicitly be found by the comparison among
$\alpha =1.2\times 10^{-2}$, which can explicitly be found by the comparison among ![]() $(b)$ (where
$(b)$ (where ![]() $t=80$) in figure 14. This corresponds to the observation that the sparse model cannot reproduce the trajectory well in figure 13.
$t=80$) in figure 14. This corresponds to the observation that the sparse model cannot reproduce the trajectory well in figure 13.
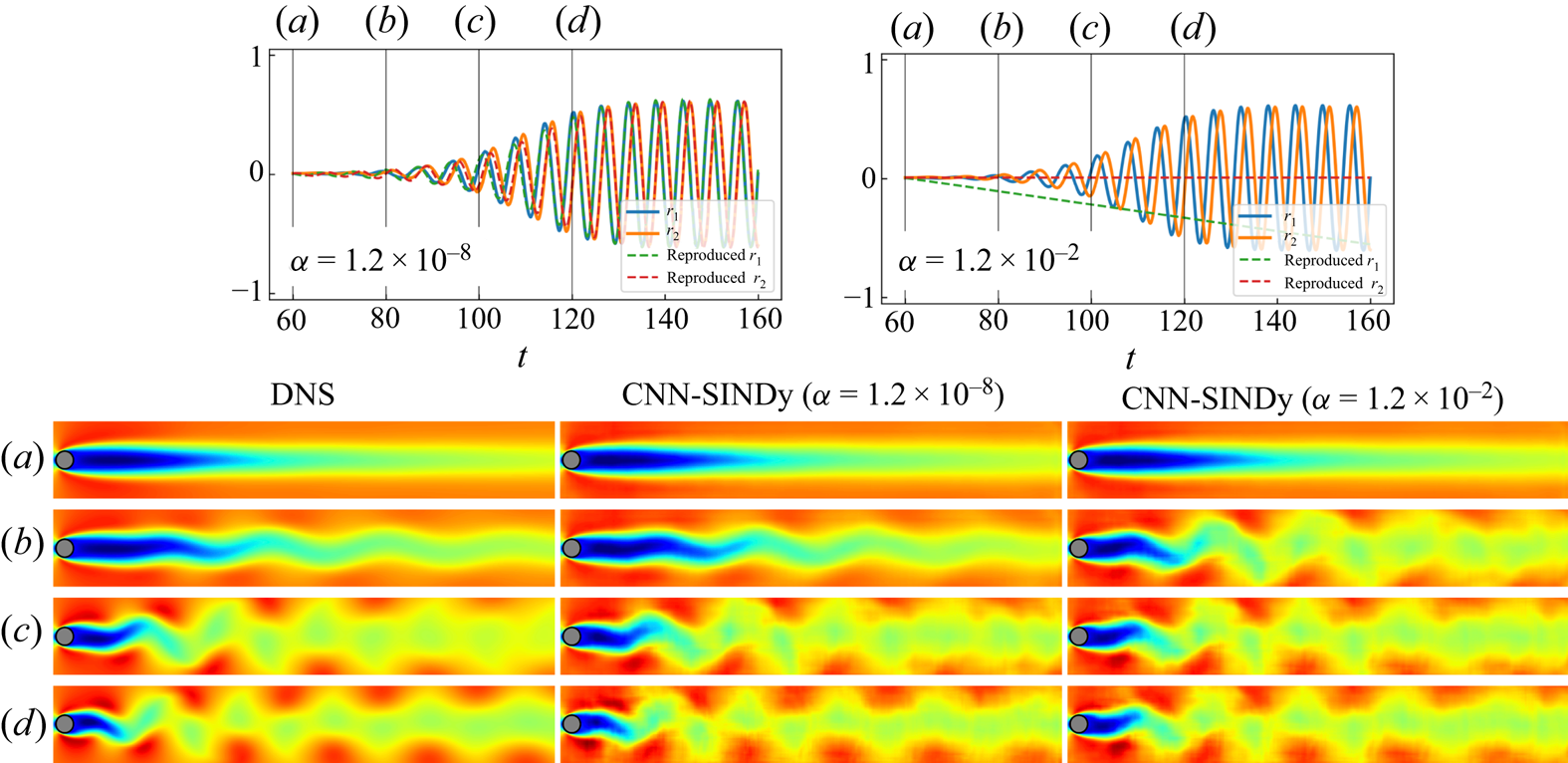
Figure 14. Time history of latent vector and the temporal evolution of the wake of DNS and the reproduced field at ![]() $(a)$
$(a)$ ![]() $t=60$,
$t=60$, ![]() $(b)$
$(b)$ ![]() $t=80$,
$t=80$, ![]() $(c)$
$(c)$ ![]() $t=100$ and
$t=100$ and ![]() $(d)$
$(d)$ ![]() $t=120$.
$t=120$.
3.3. Example 3: two-parallel cylinders wake
To demonstrate the applicability of the present CNN-SINDy-based ROM to more complex wake flows, let us here consider a flow around two-parallel cylinders whose radii are different from each other (Morimoto et al. Reference Morimoto, Fukami, Zhang and Fukagata2020b, Reference Morimoto, Fukami, Zhang, Nair and Fukagata2021), as presented in figure 1. Unlike the wake dynamics of two identical circular cylinders as described in Kang (Reference Kang2003), the coupled wakes behind two side-by-side uneven cylinders exhibits more complex vortex interactions, due to the mismatch in their individual shedding frequencies. Training flow snapshots are prepared with a DNS with the open-source computational fluid dynamics (known as CFD) toolbox OpenFOAM (Weller et al. Reference Weller, Tabor, Jasak and Fureby1998), using second-order discretization schemes in both time and space. We arrange the two circular cylinders with a size ratio of ![]() $r$ and a gap of
$r$ and a gap of ![]() $gD$, where
$gD$, where ![]() $g$ is the gap ratio and
$g$ is the gap ratio and ![]() $D$ is the diameter of the lower cylinder. The Reynolds number is fixed at
$D$ is the diameter of the lower cylinder. The Reynolds number is fixed at ![]() $Re_D=100$. The two cylinders are placed
$Re_D=100$. The two cylinders are placed ![]() $20D$ downstream of the inlet where a uniform flow with velocity
$20D$ downstream of the inlet where a uniform flow with velocity ![]() $U_{\infty }$ is prescribed, and
$U_{\infty }$ is prescribed, and ![]() $40D$ upstream of the outlet with zero pressure. The side boundaries are specified as slip and are
$40D$ upstream of the outlet with zero pressure. The side boundaries are specified as slip and are ![]() $40D$ apart. The time steps for the DNS and the snapshot sampling are, respectively, 0.01 and 0.1. A notable feature of wakes associated with the present two-cylinder position is complex wake behaviour caused by varying the size ratio
$40D$ apart. The time steps for the DNS and the snapshot sampling are, respectively, 0.01 and 0.1. A notable feature of wakes associated with the present two-cylinder position is complex wake behaviour caused by varying the size ratio ![]() $r$ and the gap ratio
$r$ and the gap ratio ![]() $g$ (Morimoto et al. Reference Morimoto, Fukami, Zhang and Fukagata2020b, Reference Morimoto, Fukami, Zhang, Nair and Fukagata2021). In the present study, the wake with the combination of
$g$ (Morimoto et al. Reference Morimoto, Fukami, Zhang and Fukagata2020b, Reference Morimoto, Fukami, Zhang, Nair and Fukagata2021). In the present study, the wake with the combination of ![]() $\{r,g\}=\{1.15,2.0\}$, which is a quasi-periodic in time, is considered for the demonstration. For the training of both the CNN-AE and the SINDy, we use 2000 snapshots. The vorticity field
$\{r,g\}=\{1.15,2.0\}$, which is a quasi-periodic in time, is considered for the demonstration. For the training of both the CNN-AE and the SINDy, we use 2000 snapshots. The vorticity field ![]() $\omega$ is used as a target attribute in this example.
$\omega$ is used as a target attribute in this example.
Prior to the use of SINDy, let us determine the size of latent variables ![]() $n_r$ of this example, as summarized in figure 15. We here construct AEs with two
$n_r$ of this example, as summarized in figure 15. We here construct AEs with two ![]() $n_r$ cases:
$n_r$ cases: ![]() $n_r=3$ and
$n_r=3$ and ![]() $n_r=4$. As presented in figure 15
$n_r=4$. As presented in figure 15![]() $(a)$, the recovered flow fields through the AE-based low-dimensionalization are in reasonable agreement with the reference DNS snapshots. Quantitatively speaking, the
$(a)$, the recovered flow fields through the AE-based low-dimensionalization are in reasonable agreement with the reference DNS snapshots. Quantitatively speaking, the ![]() $L_2$ error norms between the reference and the decoded fields are approximately 14 % and 5 % for each case. Although both models achieve the smooth spatial reconstruction, we can find the significant difference by focusing on their temporal behaviours in figure 15
$L_2$ error norms between the reference and the decoded fields are approximately 14 % and 5 % for each case. Although both models achieve the smooth spatial reconstruction, we can find the significant difference by focusing on their temporal behaviours in figure 15![]() $(b)$. While the time trace with
$(b)$. While the time trace with ![]() $n_r=4$ shows smooth variations for all four variables, the curves with
$n_r=4$ shows smooth variations for all four variables, the curves with ![]() $n_r=3$ exhibit a shaky behaviour despite the quasi-periodic nature of the flow. This is caused by the higher error level of the
$n_r=3$ exhibit a shaky behaviour despite the quasi-periodic nature of the flow. This is caused by the higher error level of the ![]() $n_r=3$ case. Furthermore, it is also known that a high-error level due to an overcompression via AE is highly influential for a temporal prediction of them since there should be exposure bias (Endo, Tomobe & Yasuoka Reference Endo, Tomobe and Yasuoka2018) occurring by a temporal integration (Hasegawa et al. Reference Hasegawa, Fukami, Murata and Fukagata2020a,Reference Hasegawa, Fukami, Murata and Fukagatab; Nakamura et al. Reference Nakamura, Fukami, Hasegawa, Nabae and Fukagata2021). In what follows, we use the AE with
$n_r=3$ case. Furthermore, it is also known that a high-error level due to an overcompression via AE is highly influential for a temporal prediction of them since there should be exposure bias (Endo, Tomobe & Yasuoka Reference Endo, Tomobe and Yasuoka2018) occurring by a temporal integration (Hasegawa et al. Reference Hasegawa, Fukami, Murata and Fukagata2020a,Reference Hasegawa, Fukami, Murata and Fukagatab; Nakamura et al. Reference Nakamura, Fukami, Hasegawa, Nabae and Fukagata2021). In what follows, we use the AE with ![]() $n_r=4$ for the SINDy-based ROM.
$n_r=4$ for the SINDy-based ROM.

Figure 15. Autoencoder-based low-dimensionalization for the wake of the two-parallel cylinders. ![]() $(a)$ Comparison of the reference DNS, the decoded field with
$(a)$ Comparison of the reference DNS, the decoded field with ![]() $n_r=3$ and the decoded field with
$n_r=3$ and the decoded field with ![]() $n_r=4$. The values underneath the contours indicate the
$n_r=4$. The values underneath the contours indicate the ![]() $L_2$ error norm.
$L_2$ error norm. ![]() $(b)$ Time series of the latent variables with
$(b)$ Time series of the latent variables with ![]() $n_r=3$ and 4.
$n_r=3$ and 4.
Let us perform SINDy with TLSA and Alasso for the AE latent variables with ![]() $n_r=4$. For the construction of a library matrix of this example, we include up to third-order terms in terms of four latent variables. The relationship between the sparsity constant
$n_r=4$. For the construction of a library matrix of this example, we include up to third-order terms in terms of four latent variables. The relationship between the sparsity constant ![]() $\alpha$ and the number of terms in identified equations is examined in figure 16. Similarly to the previous two examples with a single cylinder, the trends for TLSA and Alasso are different from each other. Note that one can only refer to this map to check the sparsity trend of the identified equation, since there is no model equation. To validate the fidelity of the equations, we need to integrate identified equations and decode a flow field using the decoder part of AE.
$\alpha$ and the number of terms in identified equations is examined in figure 16. Similarly to the previous two examples with a single cylinder, the trends for TLSA and Alasso are different from each other. Note that one can only refer to this map to check the sparsity trend of the identified equation, since there is no model equation. To validate the fidelity of the equations, we need to integrate identified equations and decode a flow field using the decoder part of AE.
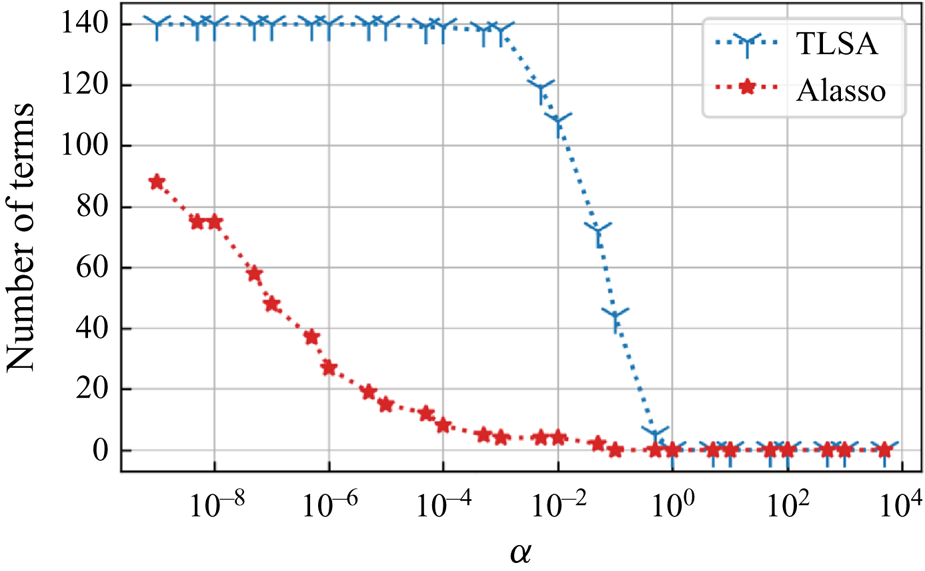
Figure 16. The relationship between the sparsity constant ![]() $\alpha$ and the number of terms in identified equations via SINDys with TLSA and Alasso for the two-parallel cylinder wake example.
$\alpha$ and the number of terms in identified equations via SINDys with TLSA and Alasso for the two-parallel cylinder wake example.
The identified equations via the TLSA-based SINDy are investigated in figure 17. As examples, the cases with ![]() $\alpha =0.1$ and 0.5 are shown. The case with
$\alpha =0.1$ and 0.5 are shown. The case with ![]() $\alpha =1$ which contains nonlinear terms shows a diverging behaviour at
$\alpha =1$ which contains nonlinear terms shows a diverging behaviour at ![]() $t\approx 90$. The sparse equation obtained with
$t\approx 90$. The sparse equation obtained with ![]() $\alpha =0.5$ can provide stable solutions for
$\alpha =0.5$ can provide stable solutions for ![]() $r_1$ and
$r_1$ and ![]() $r_2$; however, its sparseness causes the unstable integration for
$r_2$; however, its sparseness causes the unstable integration for ![]() $r_3$ and
$r_3$ and ![]() $r_4$. Note in passing that the TLSA-based modelling cannot identify the stable solution although we have carefully examined the influence on the sparsity factors for other cases not shown here.
$r_4$. Note in passing that the TLSA-based modelling cannot identify the stable solution although we have carefully examined the influence on the sparsity factors for other cases not shown here.

Figure 17. Integration of the identified equations via the TLSA-based SINDy for the two-parallel cylinder wake example. The cases are ![]() $(a)$ TLSA,
$(a)$ TLSA, ![]() $\alpha = 0.1$ and
$\alpha = 0.1$ and ![]() $(b)$ TLSA,
$(b)$ TLSA, ![]() $\alpha = 0.5$.
$\alpha = 0.5$.
We then use Alasso as a regression function of SINDy, as summarized in figure 18. The cases with ![]() $\alpha =5\times 10^{-7}$ and
$\alpha =5\times 10^{-7}$ and ![]() $10^{-6}$ are shown. The identified equation with
$10^{-6}$ are shown. The identified equation with ![]() $\alpha =5\times 10^{-7}$ can successfully be integrated and its temporal behaviour is in good agreement with the reference curve provided by the AE-based latent variables. However, what is notable here is that the equation with
$\alpha =5\times 10^{-7}$ can successfully be integrated and its temporal behaviour is in good agreement with the reference curve provided by the AE-based latent variables. However, what is notable here is that the equation with ![]() $\alpha =10^{-6}$ shows the decaying behaviour with an increasing of the integration window despite the equation form being very similar to the case with
$\alpha =10^{-6}$ shows the decaying behaviour with an increasing of the integration window despite the equation form being very similar to the case with ![]() $\alpha =5\times 10^{-7}$. Some nonlinear terms are eliminated due to the slight increase in the sparsity constant. These results indicate the importance of the careful choice for both regression functions and the sparsity constants associated with them.
$\alpha =5\times 10^{-7}$. Some nonlinear terms are eliminated due to the slight increase in the sparsity constant. These results indicate the importance of the careful choice for both regression functions and the sparsity constants associated with them.

Figure 18. Integration of the identified equations via the Alasso-based SINDy for the two-parallel cylinder wake example. The cases are ![]() $(a)$ Alasso,
$(a)$ Alasso, ![]() $\alpha =5\times 10^{-7}$ and
$\alpha =5\times 10^{-7}$ and ![]() $(b)$ Alasso,
$(b)$ Alasso, ![]() $\alpha =10^{-6}$.
$\alpha =10^{-6}$.
Based on the results above, the integrated variables with the case of Alasso with ![]() $\alpha =5\times 10^{-7}$ are fed into the CNN decoder, as presented in figure 19. The reproduced flow fields are in reasonable agreement with the reference DNS data, although there is a slight offset due to numerical integration. Hence, the present reduced-order model is able to achieve a reasonable wake reconstruction by following only the temporal evolution of low-dimensionalized vector and caring the selection of parameters, which is akin to the observation of single cylinder cases.
$\alpha =5\times 10^{-7}$ are fed into the CNN decoder, as presented in figure 19. The reproduced flow fields are in reasonable agreement with the reference DNS data, although there is a slight offset due to numerical integration. Hence, the present reduced-order model is able to achieve a reasonable wake reconstruction by following only the temporal evolution of low-dimensionalized vector and caring the selection of parameters, which is akin to the observation of single cylinder cases.
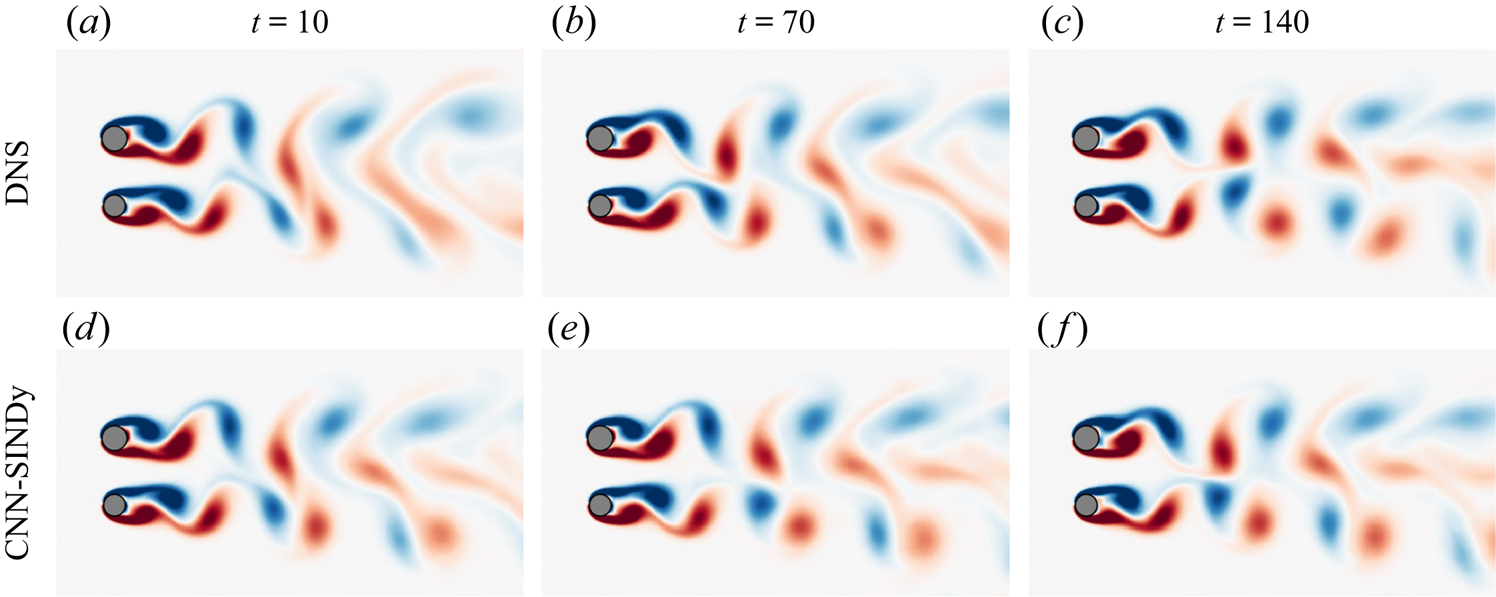
Figure 19. Reproduced fields with the CNN-SINDy-based ROM of the two-parallel cylinders example. The case of Alasso with ![]() $\alpha =5\times 10^{-7}$ is used for SINDy. The DNS flow fields are also shown for the comparison.
$\alpha =5\times 10^{-7}$ is used for SINDy. The DNS flow fields are also shown for the comparison.
3.4. Outlook: nine-equation shear flow model
One of the remaining issues of the present CNN-SINDy model is the applicability to flows where a lot of spatial modes are required to reconstruct the flow, e.g. turbulence. With the current scheme for the CNN-AE, it is difficult to compress turbulent flow data while keeping the information of high-dimensional dynamics (Murata et al. Reference Murata, Fukami and Fukagata2020). We have also recently reported that the difficulty for turbulence low-dimensionalization still remains even if we use a customized AE, although it can achieve the better mapping than that by conventional AE and POD (Fukami, Nakamura & Fukagata Reference Fukami, Nakamura and Fukagata2020c). In addition, the number of terms in a coefficient matrix must be drastically increased for the turbulent case unless the flow can be expressed with a smaller number of modes. Hence, our next question here is ‘can we also use SINDy if a turbulent flow can be mapped into a smaller number of modes?’. In this section, let us consider a nine-equation turbulent shear flow model between infinite parallel free-slip walls under a sinusoidal body force (Moehlis, Faisst & Eckhardt Reference Moehlis, Faisst and Eckhardt2004) as the preliminary example for the application to turbulence with low number of modes.
In the nine-equation model, various statistics, including mean velocity profile, streaks and vortex structures, can be represented with only nine Fourier modes ![]() ${\boldsymbol u}_j({\boldsymbol x})$. Analogous to POD, the flow fields can be mathematically expressed with a superposition of temporal coefficients and modes such that
${\boldsymbol u}_j({\boldsymbol x})$. Analogous to POD, the flow fields can be mathematically expressed with a superposition of temporal coefficients and modes such that
 \begin{equation} {\boldsymbol u}({\boldsymbol x},t) = \sum_{j=1}^{9} a_j(t){\boldsymbol u}_j({\boldsymbol x}). \end{equation}
\begin{equation} {\boldsymbol u}({\boldsymbol x},t) = \sum_{j=1}^{9} a_j(t){\boldsymbol u}_j({\boldsymbol x}). \end{equation}Here, nine ordinary differential equations for the nine mode coefficients are as follows:
 \begin{gather} \dfrac{\textrm{d}a_2}{\textrm{d}t}={-}Re^{{-}1}\left(\dfrac{4\mu^{2}}{3}+\gamma\right)a_2+\dfrac{5\sqrt{2}}{3\sqrt{3}}\dfrac{\gamma^{2}}{\kappa_{\zeta\gamma}}a_4a_6-\dfrac{\gamma^{2}}{\sqrt{6}\kappa_{\zeta\gamma}}a_5a_7-\dfrac{\zeta\mu\gamma}{\sqrt{6}\kappa_{\zeta\gamma}\kappa_{\zeta\mu\gamma}}a_5a_8\nonumber\\ -\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\mu\gamma}}a_1a_3-\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\mu\gamma}}a_3a_9, \end{gather}
\begin{gather} \dfrac{\textrm{d}a_2}{\textrm{d}t}={-}Re^{{-}1}\left(\dfrac{4\mu^{2}}{3}+\gamma\right)a_2+\dfrac{5\sqrt{2}}{3\sqrt{3}}\dfrac{\gamma^{2}}{\kappa_{\zeta\gamma}}a_4a_6-\dfrac{\gamma^{2}}{\sqrt{6}\kappa_{\zeta\gamma}}a_5a_7-\dfrac{\zeta\mu\gamma}{\sqrt{6}\kappa_{\zeta\gamma}\kappa_{\zeta\mu\gamma}}a_5a_8\nonumber\\ -\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\mu\gamma}}a_1a_3-\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\mu\gamma}}a_3a_9, \end{gather} \begin{gather} \dfrac{\textrm{d}a_3}{\textrm{d}t}={-}\dfrac{\mu^{2}+\gamma^{2}}{Re}a_3+\dfrac{2}{\sqrt{6}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}(a_4a_7+a_5a_6)\nonumber\\ +\dfrac{\mu^{2}(3\zeta^{2}+\gamma^{2})-3\gamma^{2}(\zeta^{2}+\gamma^{2})}{\sqrt{6}\kappa_{\zeta\gamma}\kappa_{\mu\gamma}\kappa_{\zeta\mu\gamma}}a_4a_8, \end{gather}
\begin{gather} \dfrac{\textrm{d}a_3}{\textrm{d}t}={-}\dfrac{\mu^{2}+\gamma^{2}}{Re}a_3+\dfrac{2}{\sqrt{6}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}(a_4a_7+a_5a_6)\nonumber\\ +\dfrac{\mu^{2}(3\zeta^{2}+\gamma^{2})-3\gamma^{2}(\zeta^{2}+\gamma^{2})}{\sqrt{6}\kappa_{\zeta\gamma}\kappa_{\mu\gamma}\kappa_{\zeta\mu\gamma}}a_4a_8, \end{gather} \begin{gather} \dfrac{\textrm{d}a_4}{\textrm{d}t}={-}\dfrac{3\zeta^{2}+4\mu^{2}}{3Re}a_4-\dfrac{\zeta}{\sqrt{6}}a_1a_5-\dfrac{10}{3\sqrt{6}}\dfrac{\zeta^{2}}{\kappa_{\zeta\gamma}}a_2a_6\nonumber\\ -\sqrt{\dfrac{3}{2}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_7-\sqrt{\dfrac{3}{2}}\dfrac{\zeta^{2}\mu^{2}}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}\kappa_{\zeta\mu\gamma}}a_3a_8-\dfrac{\zeta}{\sqrt{6}}a_5a_9, \end{gather}
\begin{gather} \dfrac{\textrm{d}a_4}{\textrm{d}t}={-}\dfrac{3\zeta^{2}+4\mu^{2}}{3Re}a_4-\dfrac{\zeta}{\sqrt{6}}a_1a_5-\dfrac{10}{3\sqrt{6}}\dfrac{\zeta^{2}}{\kappa_{\zeta\gamma}}a_2a_6\nonumber\\ -\sqrt{\dfrac{3}{2}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_7-\sqrt{\dfrac{3}{2}}\dfrac{\zeta^{2}\mu^{2}}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}\kappa_{\zeta\mu\gamma}}a_3a_8-\dfrac{\zeta}{\sqrt{6}}a_5a_9, \end{gather} \begin{gather} \dfrac{\textrm{d}a_5}{\textrm{d}t}={-}\dfrac{\zeta^{2}+\mu^{2}}{Re}a_5+\dfrac{\zeta}{\sqrt{6}}a_1a_4+\dfrac{\zeta^{2}}{\sqrt{6}\kappa_{\zeta\gamma}}a_2a_7\nonumber\\ -\dfrac{\zeta\mu\gamma}{\sqrt{6}\kappa_{\zeta\gamma}\kappa_{\zeta\mu\gamma}}a_2a_8+\dfrac{\zeta}{\sqrt{6}}a_4a_9+\dfrac{2}{\sqrt{6}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_6, \end{gather}
\begin{gather} \dfrac{\textrm{d}a_5}{\textrm{d}t}={-}\dfrac{\zeta^{2}+\mu^{2}}{Re}a_5+\dfrac{\zeta}{\sqrt{6}}a_1a_4+\dfrac{\zeta^{2}}{\sqrt{6}\kappa_{\zeta\gamma}}a_2a_7\nonumber\\ -\dfrac{\zeta\mu\gamma}{\sqrt{6}\kappa_{\zeta\gamma}\kappa_{\zeta\mu\gamma}}a_2a_8+\dfrac{\zeta}{\sqrt{6}}a_4a_9+\dfrac{2}{\sqrt{6}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_6, \end{gather} \begin{gather} \dfrac{\textrm{d}a_6}{\textrm{d}t}={-}\dfrac{3\zeta^{2}+4\mu^{2}+3\gamma^{2}}{3Re}a_6+\dfrac{\zeta}{\sqrt{6}}a_1a_7+\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\zeta\mu\gamma}}a_1a_8\nonumber\\ +\dfrac{10}{3\sqrt{6}}\dfrac{\zeta^{2}-\gamma^{2}}{\kappa_{\zeta\gamma}}a_2a_4-2\sqrt{\dfrac{2}{3}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_5+\dfrac{\zeta}{\sqrt{6}}a_7a_9+\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\zeta\mu\gamma}}a_8a_9, \end{gather}
\begin{gather} \dfrac{\textrm{d}a_6}{\textrm{d}t}={-}\dfrac{3\zeta^{2}+4\mu^{2}+3\gamma^{2}}{3Re}a_6+\dfrac{\zeta}{\sqrt{6}}a_1a_7+\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\zeta\mu\gamma}}a_1a_8\nonumber\\ +\dfrac{10}{3\sqrt{6}}\dfrac{\zeta^{2}-\gamma^{2}}{\kappa_{\zeta\gamma}}a_2a_4-2\sqrt{\dfrac{2}{3}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_5+\dfrac{\zeta}{\sqrt{6}}a_7a_9+\sqrt{\dfrac{3}{2}}\dfrac{\mu\gamma}{\kappa_{\zeta\mu\gamma}}a_8a_9, \end{gather} \begin{gather} \dfrac{\textrm{d}a_7}{\textrm{d}t}={-}\dfrac{\zeta^{2}+\mu^{2}+\gamma^{2}}{Re}a_7-\dfrac{\zeta}{\sqrt{6}}(a_1a_6+a_6a_9)\nonumber\\ +\dfrac{1}{\sqrt{6}}\dfrac{\gamma^{2}-\zeta^{2}}{\kappa_{\zeta\gamma}}a_2a_5+\dfrac{1}{\sqrt{6}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_4, \end{gather}
\begin{gather} \dfrac{\textrm{d}a_7}{\textrm{d}t}={-}\dfrac{\zeta^{2}+\mu^{2}+\gamma^{2}}{Re}a_7-\dfrac{\zeta}{\sqrt{6}}(a_1a_6+a_6a_9)\nonumber\\ +\dfrac{1}{\sqrt{6}}\dfrac{\gamma^{2}-\zeta^{2}}{\kappa_{\zeta\gamma}}a_2a_5+\dfrac{1}{\sqrt{6}}\dfrac{\zeta\mu\gamma}{\kappa_{\zeta\gamma}\kappa_{\mu\gamma}}a_3a_4, \end{gather}
where ![]() $\zeta$,
$\zeta$, ![]() $\mu$ and
$\mu$ and ![]() $\gamma$ are constant values,
$\gamma$ are constant values, ![]() $\kappa _{\zeta \gamma }=\sqrt {\zeta ^{2}+\gamma ^{2}}$,
$\kappa _{\zeta \gamma }=\sqrt {\zeta ^{2}+\gamma ^{2}}$, ![]() $\kappa _{\mu \gamma }=\sqrt {\mu ^{2}+\gamma ^{2}}$,
$\kappa _{\mu \gamma }=\sqrt {\mu ^{2}+\gamma ^{2}}$, ![]() $\kappa _{\zeta \mu \gamma }=\sqrt {\zeta ^{2}+\mu ^{2}+\gamma ^{2}}$. These coefficients are multiplied to corresponding Fourier modes which have individual roles in reconstructing a flow, e.g. basic profile, streak and spanwise flows. We refer enthusiastic readers to Moehlis et al. (Reference Moehlis, Faisst and Eckhardt2004) for details.
$\kappa _{\zeta \mu \gamma }=\sqrt {\zeta ^{2}+\mu ^{2}+\gamma ^{2}}$. These coefficients are multiplied to corresponding Fourier modes which have individual roles in reconstructing a flow, e.g. basic profile, streak and spanwise flows. We refer enthusiastic readers to Moehlis et al. (Reference Moehlis, Faisst and Eckhardt2004) for details.
In this section, we aim to obtain the coefficient matrix for the simultaneous time differential equations (3.5) to (3.13) using SINDy. In the following, let us consider the Reynolds number based on the channel half-height ![]() $\delta$ and laminar velocity
$\delta$ and laminar velocity ![]() $U_0$ at a distance of
$U_0$ at a distance of ![]() $\delta /2$ from the top wall set to
$\delta /2$ from the top wall set to ![]() $Re = 400$. The initial condition for numerical integration of the equations above is
$Re = 400$. The initial condition for numerical integration of the equations above is ![]() $(a^{0}_1,a^{0}_1,a^{0}_2,a^{0}_3,a^{0}_4,a^{0}_5,a^{0}_6,a^{0}_7,a^{0}_8,a^{0}_9)=(1, 0.07066, -0.07076, 0, 0, 0, 0, 0)$ with a random small perturbation for
$(a^{0}_1,a^{0}_1,a^{0}_2,a^{0}_3,a^{0}_4,a^{0}_5,a^{0}_6,a^{0}_7,a^{0}_8,a^{0}_9)=(1, 0.07066, -0.07076, 0, 0, 0, 0, 0)$ with a random small perturbation for ![]() $a_4$, which is the same set up as the reference code by Srinivasan et al. (Reference Srinivasan, Guastoni, Azizpour, Schlatter and Vinuesa2019). The lengths and the number of grids of the computational domain are set to
$a_4$, which is the same set up as the reference code by Srinivasan et al. (Reference Srinivasan, Guastoni, Azizpour, Schlatter and Vinuesa2019). The lengths and the number of grids of the computational domain are set to ![]() $(L_x, L_y, L_z)=(4{\rm \pi} , 2, 2{\rm \pi} )$ and
$(L_x, L_y, L_z)=(4{\rm \pi} , 2, 2{\rm \pi} )$ and ![]() $(N_x,N_y,N_z)=(21,21,21)$, respectively. The constant values are set to
$(N_x,N_y,N_z)=(21,21,21)$, respectively. The constant values are set to ![]() $(\zeta , \mu , \gamma )=(2{\rm \pi} /L_x, {\rm \pi}/2, 2{\rm \pi} /L_z)$ and the time step is 0.5. Examples of streamwise-averaged velocity
$(\zeta , \mu , \gamma )=(2{\rm \pi} /L_x, {\rm \pi}/2, 2{\rm \pi} /L_z)$ and the time step is 0.5. Examples of streamwise-averaged velocity ![]() $u_x$ contour and velocity
$u_x$ contour and velocity ![]() $u_y$ contour at the midplane with the temporal evolution of the amplitudes
$u_y$ contour at the midplane with the temporal evolution of the amplitudes ![]() $a_i$ and the pairwise correlations of the present nine coefficients are shown in figure 20. The chaotic nature of the considered problem can be seen. For performing SINDy, we use 10 000 discretized coefficients as the training data.
$a_i$ and the pairwise correlations of the present nine coefficients are shown in figure 20. The chaotic nature of the considered problem can be seen. For performing SINDy, we use 10 000 discretized coefficients as the training data.
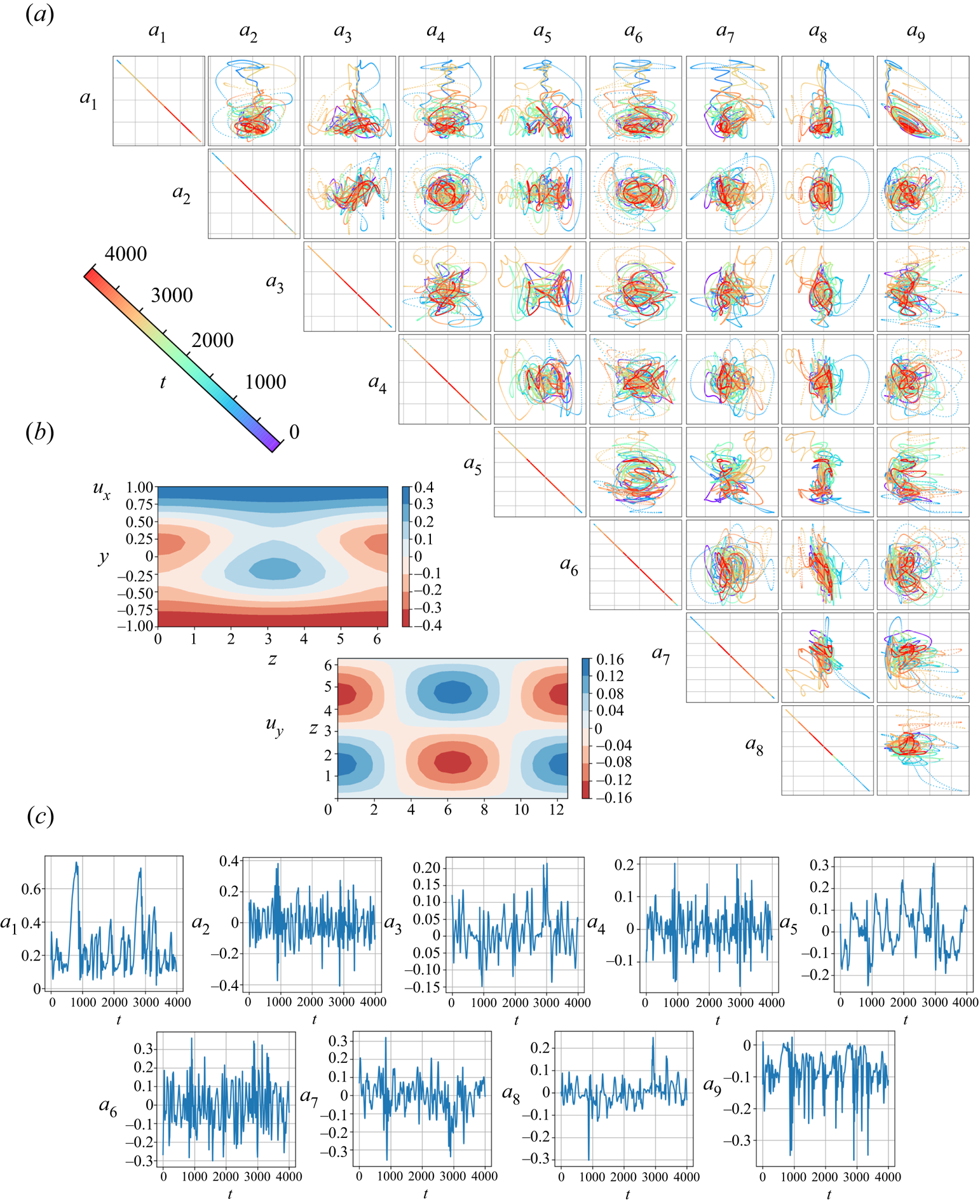
Figure 20. ![]() $(a)$ Pairwise correlations of nine coefficients.
$(a)$ Pairwise correlations of nine coefficients. ![]() $(b)$ Example contours of velocity
$(b)$ Example contours of velocity ![]() $u_x$ and velocity
$u_x$ and velocity ![]() $u_y$ at midplane.
$u_y$ at midplane. ![]() $(c)$ Temporal evolution of amplitudes
$(c)$ Temporal evolution of amplitudes ![]() $a_i$.
$a_i$.
The SINDy in this section is also performed with TLSA and Alasso following the discussions above. Since the equations for the temporal coefficients are constructed up to second-order terms, the coefficient matrix also includes up to second-order terms, as shown in figure 21![]() $(a)$. The total number of terms considered here is 55. The results with TLSA and Alasso are summarized in figure 21
$(a)$. The total number of terms considered here is 55. The results with TLSA and Alasso are summarized in figure 21![]() $(b)$. The matrices located in the right-hand area correspond to the coefficient matrix in figure 21
$(b)$. The matrices located in the right-hand area correspond to the coefficient matrix in figure 21![]() $(a)$. Similar to the results above, the model using TLSA has some huge values due to a lack of penalty terms. Especially, the effects by overfitting can be seen for the low-order portion. On the other hand, the remarkable ability of the SINDy can be seen with the Alasso. By giving the appropriate sparsity constant
$(a)$. Similar to the results above, the model using TLSA has some huge values due to a lack of penalty terms. Especially, the effects by overfitting can be seen for the low-order portion. On the other hand, the remarkable ability of the SINDy can be seen with the Alasso. By giving the appropriate sparsity constant ![]() $\alpha$, the governing equations can be represented successfully. The details of each magnitude of the coefficients are shown in figure 22. It is striking that the dominant terms are perfectly captured by using SINDy, although the magnitudes are slightly different. These noteworthy results indicate that a governing equation of low-dimensionalized turbulent flows can be obtained from only time series data by using SINDy with appropriate parameter selections. In other words, we may also be able to construct a machine-learning-based reduced-order model for turbulent flows with the interpretable sense as a form of equation, if a well-designed model for mapping into low-dimensional manifolds can be constructed.
$\alpha$, the governing equations can be represented successfully. The details of each magnitude of the coefficients are shown in figure 22. It is striking that the dominant terms are perfectly captured by using SINDy, although the magnitudes are slightly different. These noteworthy results indicate that a governing equation of low-dimensionalized turbulent flows can be obtained from only time series data by using SINDy with appropriate parameter selections. In other words, we may also be able to construct a machine-learning-based reduced-order model for turbulent flows with the interpretable sense as a form of equation, if a well-designed model for mapping into low-dimensional manifolds can be constructed.

Figure 21. The SINDy for the nine-equation shear flow model. ![]() $(a)$ Schematic of coefficient matrix
$(a)$ Schematic of coefficient matrix ![]() $\beta$.
$\beta$. ![]() $(b)$ Relationship between the sparsity constant
$(b)$ Relationship between the sparsity constant ![]() $\alpha$ and the number of terms with the obtained coefficient matrices.
$\alpha$ and the number of terms with the obtained coefficient matrices.
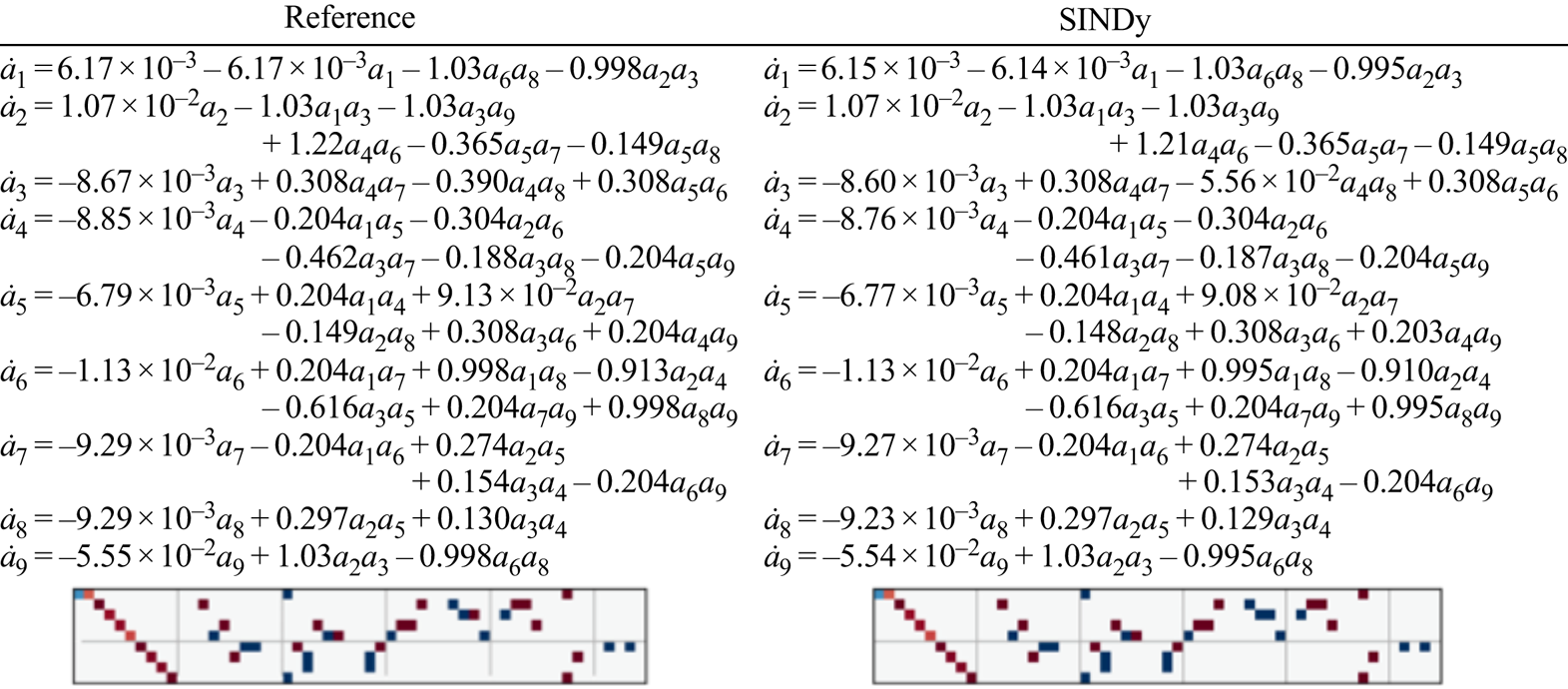
Figure 22. Comparison of the governing equation for temporal coefficients.
The robustness of SINDy against noisy measurements observed in the training pipeline for this example is finally assessed in figure 23. We here introduce the Gaussian perturbation for the training data as
where ![]() ${\boldsymbol f}$ is a target vector,
${\boldsymbol f}$ is a target vector, ![]() $\gamma$ is the magnitude of the noise and
$\gamma$ is the magnitude of the noise and ![]() ${\boldsymbol n}$ denotes the Gaussian noise. As the magnitude of noise, four cases
${\boldsymbol n}$ denotes the Gaussian noise. As the magnitude of noise, four cases ![]() $\gamma _m=\{0.05, 0.10, 0.20, 0.40\}$ are considered. With
$\gamma _m=\{0.05, 0.10, 0.20, 0.40\}$ are considered. With ![]() $\gamma = 0.05$, SINDy is still be able to identify the equation accordingly. However, the first-order terms are eliminated and unnecessary high-order terms are added with an increasing of the noise magnitude of the training data, although the whole trend of coefficient matrix can be captured. These results imply that care should be taken for noisy observations in training data depending on the problem-setting users handling, although the SINDy can guarantee its robustness for a slight perturbation.
$\gamma = 0.05$, SINDy is still be able to identify the equation accordingly. However, the first-order terms are eliminated and unnecessary high-order terms are added with an increasing of the noise magnitude of the training data, although the whole trend of coefficient matrix can be captured. These results imply that care should be taken for noisy observations in training data depending on the problem-setting users handling, although the SINDy can guarantee its robustness for a slight perturbation.

Figure 23. Noise robustness of SINDy for the nine-shear turbulent flow example.
4. Conclusion
We performed a SINDy for low-dimensionalized fluid flows and investigated influences of the regression methods and parameter considered for construction of SINDy-based modelling. Following our preliminary test, the SINDys with two regression methods, the TLSA and the Alasso, were applied to the examples of a wake around a cylinder, its transient process, and a wake of two-parallel cylinders, with a CNN-AE. The CNN-AE was employed to map high-dimensional flow data into a two-dimensional latent space using nonlinear functions. Temporal evolution of the latent dynamics could be followed well by using SINDy with an appropriate parameter selection for both examples, although the required number of terms for the coefficient matrix are varied with each other due to the difference in complexity.
Finally, we also investigated the applicability of SINDy to turbulence with low-dimensional representation using a nine-shear flow model. The governing equation could be obtained successfully by utilizing Alasso with the appropriate sparsity constant. The results indicated that ML-ROM for turbulent flows can be perhaps presented in the interpretable sense in the form of an equation, if a well-designed model for mapping high-dimensional complex flows into low-dimensional manifolds can be constructed. With regard to the low-dimensional manifolds of fluid flows, the novel work by Loiseau et al. (Reference Loiseau, Brunton and Noack2018a) discussed the nonlinear relationship between lower-order POD modes and higher-order counterparts of cylinder wake dynamics by relating it to a triadic interaction among POD modes. We may be able to borrow the concept here to investigate the possible nonlinear correlations in the data, although it will be tackled in the future since it is not easy to apply their idea directly to the nine-equation shear flow model which is composed of more complex relationships among modes. Otherwise, a combination of uncertainty quantification (Maulik et al. Reference Maulik, Fukami, Ramachandra, Fukagata and Taira2020), transfer learning (Guastoni et al. Reference Guastoni, Encinar, Schlatter, Azizpour and Vinuesa2020a; Morimoto et al. Reference Morimoto, Fukami, Zhang and Fukagata2020b) and Koopman-based frameworks (Eivazi et al. Reference Eivazi, Guastoni, Schlatter, Azizpour and Vinuesa2021) may also be possible extensions toward more practical applications.
The current results for CNN-SINDy modelling makes us sceptical about applications of CNN-AE to the flows where many spatial modes are required to represent the energetic field, e.g. turbulence, despite that recent several studies have shown its potential for unsteady laminar flows (Carlberg et al. Reference Carlberg, Jameson, Kochenderfer, Morton, Peng and Witherden2019; Agostini Reference Agostini2020; Taira et al. Reference Taira, Hemati, Brunton, Sun, Duraisamy, Bagheri, Dawson and Yeh2020; Xu & Duraisamy Reference Xu and Duraisamy2020; Bukka et al. Reference Bukka, Gupta, Magee and Jaiman2021). Since a few studies have also recently recognized the challenges of the current form of CNN-AE for turbulence (Brunton, Hemati & Taira Reference Brunton, Hemati and Taira2020; Fukami et al. Reference Fukami, Nakamura and Fukagata2020c; Glaws, King & Sprague Reference Glaws, King and Sprague2020; Nakamura et al. Reference Nakamura, Fukami, Hasegawa, Nabae and Fukagata2021), care should be taken with the choice of low-dimensionalization tools depending on the flows that users handle. Hence, the utilization of other well-sophisticated low-dimensionalization tools such as spectral POD (Towne, Schmidt & Colonius Reference Towne, Schmidt and Colonius2018; Abreu et al. Reference Abreu, Cavalieri, Schlatter, Vinuesa and Henningson2020), t-distributed stochastic neighbour embedding (Wu et al. Reference Wu, Wang, Xiao and Ling2017), hierarchical AE (Fukami et al. Reference Fukami, Nakamura and Fukagata2020c) and locally linear embedding (Roweis & Lawrence Reference Roweis and Lawrence2000; Ehlert et al. Reference Ehlert, Nayeri, Morzynski and Noack2019) can be considered to achieve better mapping of flow fields. Taking constraints for coordinates extracted via AE is also a candidate to promote the combination of AE modes and conventional flow control tools (Champion et al. Reference Champion, Lusch, Kutz and Brunton2019a; Gelß et al. Reference Gelß, Klus, Eisert and Schütte2019; Ladjal et al. Reference Ladjal, Newson and Pham2019; Jayaraman & Mamun Reference Jayaraman and Mamun2020). Finally, we believe that the results of our examples, above, enables us to have a strong motivation for future work and notice the remarkable potential of SINDy for fluid dynamics.
Acknowledgements
The authors thank Professor S. Obi, Professor K. Ando, Mr M. Morimoto, Mr T. Nakamura, Mr S. Kanehira (Keio Univ.), Mr K. Hasegawa (Keio Univ., Polimi) and Professor K. Taira (UCLA) for fruitful discussions.
Funding
This work was supported from the Japan Society for the Promotion of Science (KAKENHI grant numbers: 18H03758, 21H05007).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Regression methods for SINDy
As introduced in § 1, the regression method used to obtain the coefficient matrix ![]() $\varXi$ is important since the resultant coefficient matrix
$\varXi$ is important since the resultant coefficient matrix ![]() $\varXi$ may vary with the choice of regression method. Here, let us consider a typical regression problem,
$\varXi$ may vary with the choice of regression method. Here, let us consider a typical regression problem,
where ![]() $\boldsymbol {P}$ and
$\boldsymbol {P}$ and ![]() $\boldsymbol {Q}$ denote the response variables and the explanatory variable, respectively. In this problem, we aim to obtain the coefficient matrix
$\boldsymbol {Q}$ denote the response variables and the explanatory variable, respectively. In this problem, we aim to obtain the coefficient matrix ![]() $\boldsymbol {\beta }$ representing the relationships between
$\boldsymbol {\beta }$ representing the relationships between ![]() $\boldsymbol {P}$ and
$\boldsymbol {P}$ and ![]() $\boldsymbol {Q}$. Using the linear regression method, an optimized coefficient matrix
$\boldsymbol {Q}$. Using the linear regression method, an optimized coefficient matrix ![]() $\boldsymbol {\beta }$ can be found by minimizing the error between the left-hand and right-hand sides such that
$\boldsymbol {\beta }$ can be found by minimizing the error between the left-hand and right-hand sides such that
The TLSA, originally used in Brunton et al. (Reference Brunton, Proctor and Kutz2016a) for performing SINDy, is based on this formulation in (A2) and obtains the sparse coefficient matrix by substituting zero for the coefficient below the threshold ![]() $\alpha$. Its algorithm is summarized as algorithm 1:
$\alpha$. Its algorithm is summarized as algorithm 1:
Algorithm 1 Thresholded least square algorithm

Although the linear regression method has been widely used due to its simplicity, Hoerl & Kennard (Reference Hoerl and Kennard1970) cautioned that estimated coefficients are sometimes large in absolute value for the non-orthogonal data. This is known as the overfitting problem. As a considerable surrogate method, they proposed the Ridge regression (Hoerl & Kennard Reference Hoerl and Kennard1970). In this method, the squared value of the components in the coefficient matrix is considered as the constraint of the minimization process such that
where ![]() $\alpha$ denotes the weight of the constraint term. For uses of SINDy, the coefficient matrix
$\alpha$ denotes the weight of the constraint term. For uses of SINDy, the coefficient matrix ![]() $\boldsymbol {\beta }$ is desired to be sparse, i.e. some components are zero, so as to avoid construction of a complex model and overfitting. As the sparse regression method, Lasso (Tibshirani Reference Tibshirani1996) was proposed. With Lasso, the sum of the absolute value of components in the coefficient matrix is incorporated to determine the coefficient matrix as follows:
$\boldsymbol {\beta }$ is desired to be sparse, i.e. some components are zero, so as to avoid construction of a complex model and overfitting. As the sparse regression method, Lasso (Tibshirani Reference Tibshirani1996) was proposed. With Lasso, the sum of the absolute value of components in the coefficient matrix is incorporated to determine the coefficient matrix as follows:
If the sparsity constant ![]() $\alpha$ is set to a high value, the estimation error becomes relatively large while the coefficient matrix results in a sparse matrix.
$\alpha$ is set to a high value, the estimation error becomes relatively large while the coefficient matrix results in a sparse matrix.
The Lasso algorithm introduced above has, however, two drawbacks and there are solutions for each: the elastic net (Enet) and the Alasso, as mentioned in the introduction. Enet (Zou & Hastie Reference Zou and Hastie2005) combines ![]() $L_1$ and
$L_1$ and ![]() $L_2$ errors, i.e. those of the Ridge regression, and Lasso. The optimal coefficient
$L_2$ errors, i.e. those of the Ridge regression, and Lasso. The optimal coefficient ![]() $\boldsymbol {\beta }$ is obtained as
$\boldsymbol {\beta }$ is obtained as
 \begin{equation} \boldsymbol{\beta} = \left( 1+\frac{\alpha_2}{n} \right) \left\{ \textrm{argmin} \left\| \boldsymbol{P} - \boldsymbol{Q}\boldsymbol{\beta} \right\|^{2} + \alpha_1 \sum_j |\beta_j| + \alpha_2 \sum_j \beta_j^{2} \right\}. \end{equation}
\begin{equation} \boldsymbol{\beta} = \left( 1+\frac{\alpha_2}{n} \right) \left\{ \textrm{argmin} \left\| \boldsymbol{P} - \boldsymbol{Q}\boldsymbol{\beta} \right\|^{2} + \alpha_1 \sum_j |\beta_j| + \alpha_2 \sum_j \beta_j^{2} \right\}. \end{equation}
The following two parameters are set for the Enet: the sparsity constant ![]() $\alpha =\alpha _1+\alpha _2$ and the sparse ratio
$\alpha =\alpha _1+\alpha _2$ and the sparse ratio ![]() $\alpha _1 / (\alpha _1 + \alpha _2)$, respectively. The property for the sparsity constant
$\alpha _1 / (\alpha _1 + \alpha _2)$, respectively. The property for the sparsity constant ![]() $\alpha$ is the same as that of Lasso: a higher
$\alpha$ is the same as that of Lasso: a higher ![]() $\alpha$ results in large error and sparse estimation. The sparse ratio is the ratio of
$\alpha$ results in large error and sparse estimation. The sparse ratio is the ratio of ![]() $L_1$ and
$L_1$ and ![]() $L_2$ errors as seen its definition. The sparse model can be obtained with a high
$L_2$ errors as seen its definition. The sparse model can be obtained with a high ![]() $L_1$ ratio, although the collinearity problem may not be solved. Another solution, the Alasso (Zou Reference Zou2006), uses adaptive weights for the penalizing coefficients in
$L_1$ ratio, although the collinearity problem may not be solved. Another solution, the Alasso (Zou Reference Zou2006), uses adaptive weights for the penalizing coefficients in ![]() $L_1$ penalty term. In the Alasso,
$L_1$ penalty term. In the Alasso, ![]() $\boldsymbol {\beta }$ are given by
$\boldsymbol {\beta }$ are given by
where ![]() $w_j=(|\beta _j|)^{-\delta }$ denotes the adaptive weight with
$w_j=(|\beta _j|)^{-\delta }$ denotes the adaptive weight with ![]() $\delta >0$. The use of
$\delta >0$. The use of ![]() $w_j$ enables us to avoid the issue of multiple local minima. The weights
$w_j$ enables us to avoid the issue of multiple local minima. The weights ![]() $w_j$ and coefficients
$w_j$ and coefficients ![]() $\boldsymbol {\beta }$ are updated repeatedly like in algorithm 2:
$\boldsymbol {\beta }$ are updated repeatedly like in algorithm 2:
Algorithm 2 Adaptive Lasso

In general it is necessary to choose the appropriate value for the threshold or the sparsity constant ![]() $\alpha$ in order to obtain a desired equation which is sparse and in an interpretable form. Hence, we focus on seeking the appropriate
$\alpha$ in order to obtain a desired equation which is sparse and in an interpretable form. Hence, we focus on seeking the appropriate ![]() $\alpha$ of each regression method in this study. The algorithm for the parameter search applied to the current study is described in algorithm 3.
$\alpha$ of each regression method in this study. The algorithm for the parameter search applied to the current study is described in algorithm 3.
Algorithm 3 Parameter search

Regarding the assessment ways used in procedures 5 and 7 in algorithm 3, number of total remaining terms of the obtained equation are utilized as the evaluation index for the preliminary test. For cylinder examples, the number of total terms, the error in the amplitudes of obtained waveforms, and the error ratio in the period between the obtained wave and the solution are assessed.
Appendix B. Preliminary tests with low-dimensional problems
B.1. Pretest 1: van der Pol oscillator
As a preliminary test of performing SINDy, we consider the van der Pol oscillator (Van der Pol Reference Van der Pol1934), which has a nonlinear damping. The governing equations are
where ![]() $\kappa >0$ is a constant parameter and we set
$\kappa >0$ is a constant parameter and we set ![]() $\kappa =2$ in this preliminary test. The trajectory converges to a stable limit cycle determined by
$\kappa =2$ in this preliminary test. The trajectory converges to a stable limit cycle determined by ![]() $\kappa$ under any initial state except for the unstable point (
$\kappa$ under any initial state except for the unstable point (![]() $x=0, y=0$) as shown in figure 24.
$x=0, y=0$) as shown in figure 24.

Figure 24. Dynamics of the van der Pol oscillator with ![]() $\kappa =2$: (
$\kappa =2$: (![]() $a$) time history and (
$a$) time history and (![]() $b$) trajectory on the
$b$) trajectory on the ![]() $x - y$ plane. The initial point is set to
$x - y$ plane. The initial point is set to ![]() $(x,y)=(-2,5)$ in this example.
$(x,y)=(-2,5)$ in this example.
Let us perform SINDy with each of the four regression methods, i.e. TLSA, Lasso, Enet and Alasso, with various sparsity constants ![]() $\alpha$. Here, we use 20 000 discretized points as the training data sampled within
$\alpha$. Here, we use 20 000 discretized points as the training data sampled within ![]() $t=[0, 200]$ with the time step
$t=[0, 200]$ with the time step ![]() $\Delta t=1 \times 10^{-2}$, although we will investigate the dependence of SINDy performance on both the length of time step and the length of training data range later. The library matrix is arranged including up to the fifth-order terms. In this example, we assess candidate models by using the total number of terms contained in the obtained ordinary differential equation. As denoted in (B1) and (B2), the true model has four non-zero terms in total in two governing equations. The relationship between the total number of terms in the candidate models and
$\Delta t=1 \times 10^{-2}$, although we will investigate the dependence of SINDy performance on both the length of time step and the length of training data range later. The library matrix is arranged including up to the fifth-order terms. In this example, we assess candidate models by using the total number of terms contained in the obtained ordinary differential equation. As denoted in (B1) and (B2), the true model has four non-zero terms in total in two governing equations. The relationship between the total number of terms in the candidate models and ![]() $\alpha$ is shown in figure 25. As shown, the uses of Lasso and Enet cannot reach the true model whose total number of terms is four. On the other hand, using TLSA or Alasso, the correct governing equation can be identified. It is striking that we should choose the appropriate parameter
$\alpha$ is shown in figure 25. As shown, the uses of Lasso and Enet cannot reach the true model whose total number of terms is four. On the other hand, using TLSA or Alasso, the correct governing equation can be identified. It is striking that we should choose the appropriate parameter ![]() $\alpha$ for the correct model identification, as shown in figure 25. In this sense, the Alasso is suitable for the problem here since a wide range of
$\alpha$ for the correct model identification, as shown in figure 25. In this sense, the Alasso is suitable for the problem here since a wide range of ![]() $\alpha$, i.e.
$\alpha$, i.e. ![]() $10^{-9}\leq \alpha \leq 10^{-2}$, can provide the correct equation. The difference here is likely due to the scheme of each regression. The TLSA is unable to discard the components of
$10^{-9}\leq \alpha \leq 10^{-2}$, can provide the correct equation. The difference here is likely due to the scheme of each regression. The TLSA is unable to discard the components of ![]() $\beta$ with low
$\beta$ with low ![]() $\alpha$ values: in other words, a lot of terms remain through the iterative process. On the other hand, the Alasso can identify the dominant terms clearly thanks to adaptive weights even if
$\alpha$ values: in other words, a lot of terms remain through the iterative process. On the other hand, the Alasso can identify the dominant terms clearly thanks to adaptive weights even if ![]() $\alpha$ is relatively low.
$\alpha$ is relatively low.

Figure 25. Relationship between ![]() $\alpha$ and the number of terms, and the examples of obtained equations for four regression methods.
$\alpha$ and the number of terms, and the examples of obtained equations for four regression methods.
To investigate the dependence on the time step of the input data, SINDy is performed on the data with different time steps: ![]() $\Delta t=1 \times 10^{-2}$,
$\Delta t=1 \times 10^{-2}$, ![]() $0.1$ and
$0.1$ and ![]() $0.2$. Here, we consider only TLSA and Alasso following the aforementioned results. Note that the number of input data is different due to the time step since the integration time length is fixed to
$0.2$. Here, we consider only TLSA and Alasso following the aforementioned results. Note that the number of input data is different due to the time step since the integration time length is fixed to ![]() $t_{ max}=200$ in all cases. We have checked in our preliminary tests that this difference has no significant effect on the results. The trajectory, the results for the parameter search, and the example of obtained equations are summarized in figure 26. With the fine data, i.e.
$t_{ max}=200$ in all cases. We have checked in our preliminary tests that this difference has no significant effect on the results. The trajectory, the results for the parameter search, and the example of obtained equations are summarized in figure 26. With the fine data, i.e. ![]() $\Delta t=1 \times 10^{-2}$, the governing equations are correctly identified with some
$\Delta t=1 \times 10^{-2}$, the governing equations are correctly identified with some ![]() $\alpha$ for both methods. The true model can be found even if we use very small
$\alpha$ for both methods. The true model can be found even if we use very small ![]() $\alpha$, i.e.
$\alpha$, i.e. ![]() $\alpha =1 \times 10^{-8}$ with Alasso as mentioned before. With increasing
$\alpha =1 \times 10^{-8}$ with Alasso as mentioned before. With increasing ![]() $\Delta t$, i.e.
$\Delta t$, i.e. ![]() $\Delta t=0.1$, the coefficients of terms are slightly underestimated. Additionally, the range of
$\Delta t=0.1$, the coefficients of terms are slightly underestimated. Additionally, the range of ![]() $\alpha$ where the number of terms is correctly identified as four becomes narrower with both methods. With a wider time step, i.e.
$\alpha$ where the number of terms is correctly identified as four becomes narrower with both methods. With a wider time step, i.e. ![]() $\Delta t=0.2$, the dominant terms can be found only with Alasso. On the other hand, the true model cannot be obtained with further wider time step data, i.e.
$\Delta t=0.2$, the dominant terms can be found only with Alasso. On the other hand, the true model cannot be obtained with further wider time step data, i.e. ![]() $\Delta t=0.5$, even with Alasso, due to the temporal coarseness as shown in figure 26
$\Delta t=0.5$, even with Alasso, due to the temporal coarseness as shown in figure 26![]() $(d)$. It suggests that the data with the appropriate time step is necessary for the construction of the model. In summary, Alasso is superior in terms of its ability to correctly identify the dominant terms for a wider range of sparsity constant.
$(d)$. It suggests that the data with the appropriate time step is necessary for the construction of the model. In summary, Alasso is superior in terms of its ability to correctly identify the dominant terms for a wider range of sparsity constant.
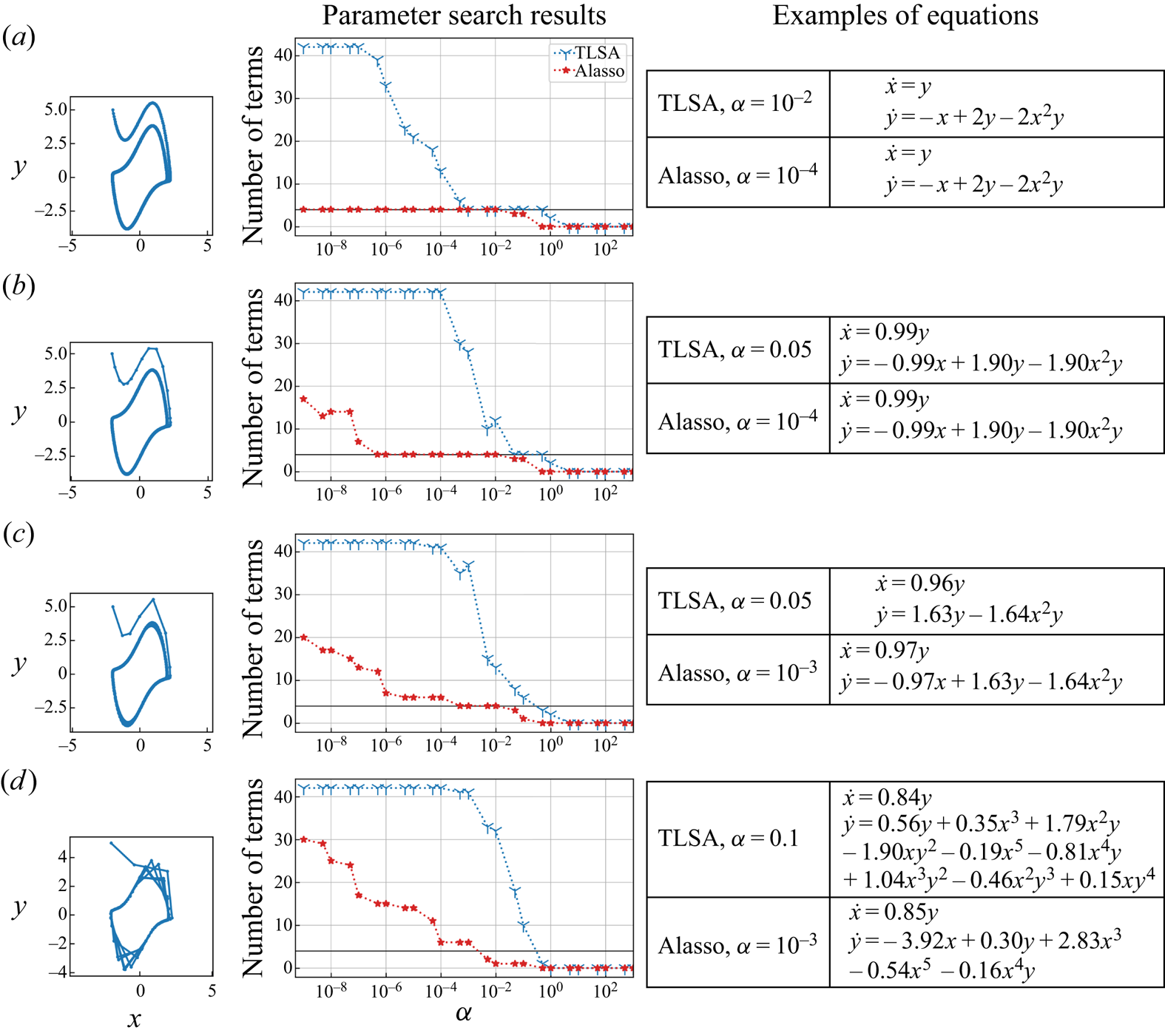
Figure 26. Trajectory on the ![]() $x - y$ plane, the relationship between
$x - y$ plane, the relationship between ![]() $\alpha$ and number of terms, and the examples of obtained equations for data for different time steps: (
$\alpha$ and number of terms, and the examples of obtained equations for data for different time steps: (![]() $a$)
$a$) ![]() $\Delta t =1 \times 10^{-2}$, 769 points/period; (
$\Delta t =1 \times 10^{-2}$, 769 points/period; (![]() $b$)
$b$) ![]() $\Delta t =0.1$, 76.9 points/period; (
$\Delta t =0.1$, 76.9 points/period; (![]() $c$)
$c$) ![]() $\Delta t =0.2$, 38.5 points/period; (
$\Delta t =0.2$, 38.5 points/period; (![]() $d$)
$d$) ![]() $\Delta t=0.5$, 15.4 points/period.
$\Delta t=0.5$, 15.4 points/period.
Let us then investigate the dependence of the performance on the length of training data range, as demonstrated in figure 27. We here consider three lengths of training data range as ![]() $(a)$
$(a)$ ![]() $t=[0, 8]$,
$t=[0, 8]$, ![]() $(b)$
$(b)$ ![]() $t=[0,12]$ and
$t=[0,12]$ and ![]() $(c)$
$(c)$ ![]() $t=[0,200]$ (baseline), while keeping the time step
$t=[0,200]$ (baseline), while keeping the time step ![]() $\Delta t=1 \times 10^{-2}$. As shown, the trends of the relationship between the sparsity constant and the number of terms in the identified equation are similar over the covered time length. In addition, the SINDys with the TLSA (
$\Delta t=1 \times 10^{-2}$. As shown, the trends of the relationship between the sparsity constant and the number of terms in the identified equation are similar over the covered time length. In addition, the SINDys with the TLSA (![]() $\alpha =1 \times 10^{-2}$) and Alasso (
$\alpha =1 \times 10^{-2}$) and Alasso (![]() $\alpha =1 \times 10^{-3}$) are able to identify the equations successfully for all time length cases. Only in the case of
$\alpha =1 \times 10^{-3}$) are able to identify the equations successfully for all time length cases. Only in the case of ![]() $t = [0,8]$, does the model identification not perform well with the Alasso around
$t = [0,8]$, does the model identification not perform well with the Alasso around ![]() $\alpha =1 \times 10^{-8}$. The time length has little effect on the model identification if the time length is more than one period.
$\alpha =1 \times 10^{-8}$. The time length has little effect on the model identification if the time length is more than one period.

Figure 27. The dependence of the performance of SINDy on the length of training data range: ![]() $(a)$
$(a)$ ![]() $t=[0, 8]$;
$t=[0, 8]$; ![]() $(b)$
$(b)$ ![]() $t=[0,12]$;
$t=[0,12]$; ![]() $(c)$
$(c)$ ![]() $t=[0,200]$ (baseline).
$t=[0,200]$ (baseline).
For considering models in which higher-order terms may be dominant due to higher nonlinearity, it will be valuable to find the way to select the appropriate potential terms that should be included in the library matrix. From this view, the dependence on the number of potential terms is investigated using the data with ![]() $\Delta t=1 \times 10^{-2}$. In the case where the maximum order of the potential terms is the fifth, the true model can be found with two regression methods, i.e. TLSA and Alasso, as shown in figure 26(
$\Delta t=1 \times 10^{-2}$. In the case where the maximum order of the potential terms is the fifth, the true model can be found with two regression methods, i.e. TLSA and Alasso, as shown in figure 26(![]() $a$). Here, the case with higher maximum order, i.e. the 15th and 20th, are also investigated as shown in figure 28. Note that there are 136 and 231 potential terms for each differential equation in these cases. For both cases with a different number of potential terms, we cannot find the true model with TLSA while the true model is identified in a wide range of
$a$). Here, the case with higher maximum order, i.e. the 15th and 20th, are also investigated as shown in figure 28. Note that there are 136 and 231 potential terms for each differential equation in these cases. For both cases with a different number of potential terms, we cannot find the true model with TLSA while the true model is identified in a wide range of ![]() $\alpha$ with Alasso. Furthermore, in the case including up to the 15th terms, some coefficients in the equation obtained by TLSA become huge. These large coefficients are due to the different functions included in the library being almost collinear.
$\alpha$ with Alasso. Furthermore, in the case including up to the 15th terms, some coefficients in the equation obtained by TLSA become huge. These large coefficients are due to the different functions included in the library being almost collinear.

Figure 28. Relationship between ![]() $\alpha$ and number of terms and the examples of obtained equations for data for different library matrices: (
$\alpha$ and number of terms and the examples of obtained equations for data for different library matrices: (![]() $a$) including up to the 15th potential terms and (
$a$) including up to the 15th potential terms and (![]() $b$) including up to the 20th potential terms.
$b$) including up to the 20th potential terms.
B.2. Pretest 2: Lorenz attractor
As the second preliminary test, we consider the problem of identifying a chaotic trajectory called the Lorenz attractor (Lorenz Reference Lorenz1963). It is written in a form of nonlinear ordinary differential equations,
Lorenz (Reference Lorenz1963) showed that the dynamics governed by the equations above shows chaotic behaviour with the certain coefficients, i.e. ![]() $(\sigma , \rho , \iota )$ = (10, 28,
$(\sigma , \rho , \iota )$ = (10, 28, ![]() $8/3$) with the initial values
$8/3$) with the initial values ![]() $(x,y,z)=(-8,8,27)$, as shown in figure 29.
$(x,y,z)=(-8,8,27)$, as shown in figure 29.

Figure 29. Dynamics of the Lorenz attractor: ![]() $(a)$ time history and
$(a)$ time history and ![]() $(b)$ trajectory.
$(b)$ trajectory.
As with the preliminary test of the van der Pol oscillator, we consider four regression methods: TLSA, Lasso, Enet and Alasso, as shown in figure 30. Note that 10 000 discretized points with ![]() $\Delta t=1 \times 10^{-2}$ from the time range of
$\Delta t=1 \times 10^{-2}$ from the time range of ![]() $t=[0,100]$ are used as the training data and the potential terms up to fifth order are considered here. Similar to the van der Pol oscillator, we can obtain the true model whose total number of terms is seven with TLSA or Alasso, although Lasso or Enet cannot identify the equation correctly. Comparing the two methods which can obtain the correct model, the range of
$t=[0,100]$ are used as the training data and the potential terms up to fifth order are considered here. Similar to the van der Pol oscillator, we can obtain the true model whose total number of terms is seven with TLSA or Alasso, although Lasso or Enet cannot identify the equation correctly. Comparing the two methods which can obtain the correct model, the range of ![]() $\alpha$, where the governing equations are identified, is wider using Alasso. We also perform SINDy with different time steps as shown in figure 31. Note that the considered time range is not changed depending on the time steps: in other words, the number of training data is changed per a considered time step, which is the same setting as that for the van der Pol example. Similarly to the case of the van der Pol oscillator, we cannot reach the correct model using TLSA unless
$\alpha$, where the governing equations are identified, is wider using Alasso. We also perform SINDy with different time steps as shown in figure 31. Note that the considered time range is not changed depending on the time steps: in other words, the number of training data is changed per a considered time step, which is the same setting as that for the van der Pol example. Similarly to the case of the van der Pol oscillator, we cannot reach the correct model using TLSA unless ![]() $\alpha$ is fine-tuned, and the coefficients are underestimated using Alasso with the wider time step data, i.e.
$\alpha$ is fine-tuned, and the coefficients are underestimated using Alasso with the wider time step data, i.e. ![]() $\Delta t=2 \times 10^{-2}$. Moreover, the dependence on how many orders are considered in the library matrix is investigated in figure 32. There are 286 or 816 potential terms for each differential equation with the case including up to the 10th- or 15th-order terms, respectively. Analogous to the van der Pol oscillator example, the true model cannot be identified with TLSA; however, we can identify the true equation using Alasso even if there are as many as 816 potential terms with an appropriate range of
$\Delta t=2 \times 10^{-2}$. Moreover, the dependence on how many orders are considered in the library matrix is investigated in figure 32. There are 286 or 816 potential terms for each differential equation with the case including up to the 10th- or 15th-order terms, respectively. Analogous to the van der Pol oscillator example, the true model cannot be identified with TLSA; however, we can identify the true equation using Alasso even if there are as many as 816 potential terms with an appropriate range of ![]() $\alpha$. Based on these results, TLSA and Alasso are selected as candidate regressions for high-dimensional complex flow problems.
$\alpha$. Based on these results, TLSA and Alasso are selected as candidate regressions for high-dimensional complex flow problems.

Figure 30. Relationship between ![]() $\alpha$ and the total number of terms, with the examples of obtained equations.
$\alpha$ and the total number of terms, with the examples of obtained equations.
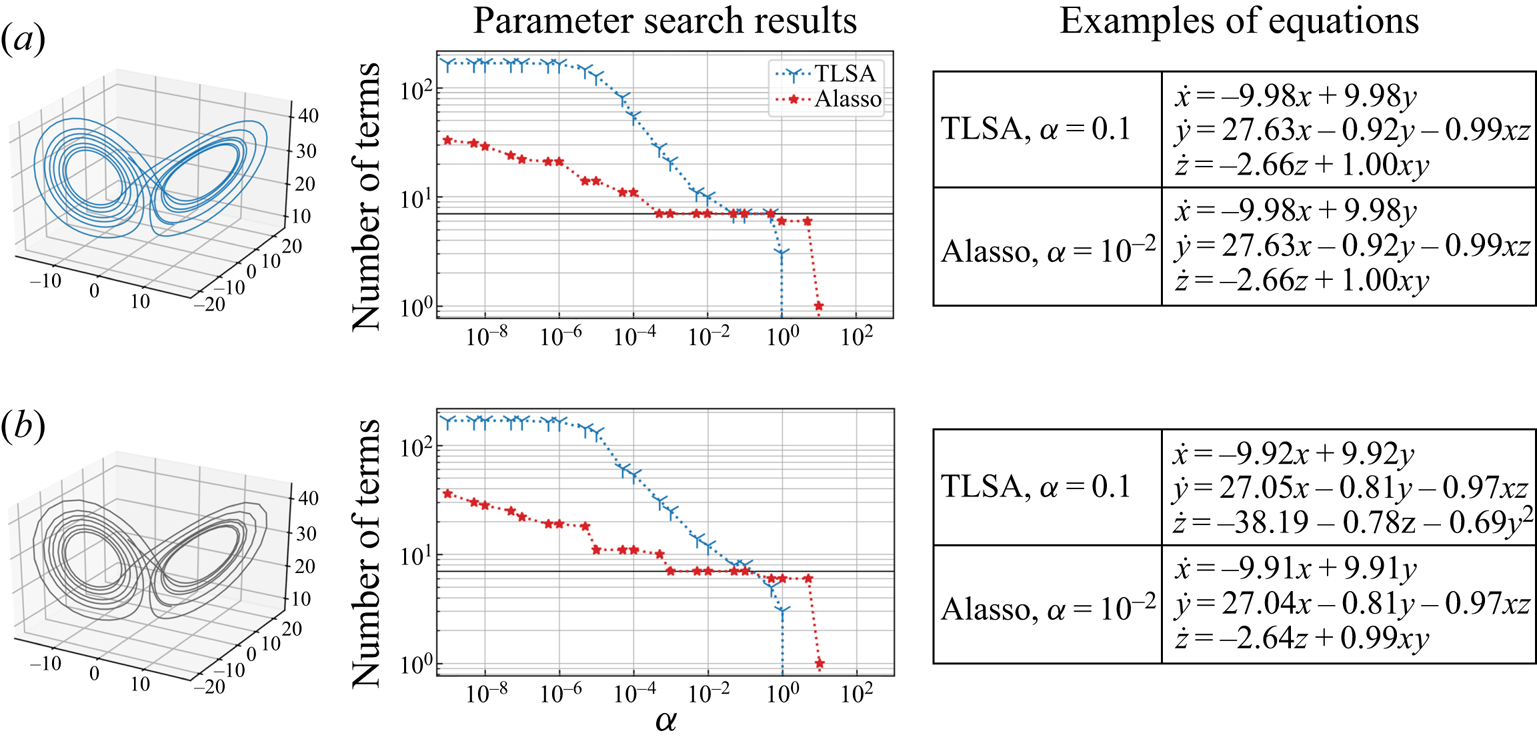
Figure 31. Trajectory on the ![]() $x - y$ plane, the relationship between
$x - y$ plane, the relationship between ![]() $\alpha$ and number of terms, and the examples of obtained equations for data for different time steps: (
$\alpha$ and number of terms, and the examples of obtained equations for data for different time steps: (![]() $a$)
$a$) ![]() $\Delta t =1 \times 10^{-2}$ and (
$\Delta t =1 \times 10^{-2}$ and (![]() $b$)
$b$) ![]() $\Delta t =2 \times 10^{-2}$.
$\Delta t =2 \times 10^{-2}$.

Figure 32. Relationship between ![]() $\alpha$ and number of terms, and the examples of obtained equations for data for different library matrices: (
$\alpha$ and number of terms, and the examples of obtained equations for data for different library matrices: (![]() $a$) including up to the 10th potential terms and (
$a$) including up to the 10th potential terms and (![]() $b$) including up to the 15th potential terms.
$b$) including up to the 15th potential terms.
In addition, we here note that the use of simple data processing (e.g. the standardization and the normalization) for both AE and SINDy pipelines may help Lasso and Enet to improve the regression ability, although it highly relies on a problem setting. Taking the data processing usually limits the model for practical uses because these data processing can only be successfully employed when we can guarantee an ergodicity, i.e. the statistical features of training data and test data are common with each other (Guastoni et al. Reference Guastoni, Güemes, Ianiro, Discetti, Schlatter, Azizpour and Vinuesa2020b; Morimoto et al. Reference Morimoto, Fukami, Zhang and Fukagata2020b). When we perform the data processing, an inverse transformation error through the normalization or standardization is usually added since parameters for the processing, e.g. minimum value, maximum value, average value and variance, may be changed over the training and test phases. Hence, toward practical applications, it is better to prepare the regression method which is robust for the amplitudes of data oscillations.