Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
de Kat, Roeland
and
Ganapathisubramani, Bharathram
2015.
Frequency–wavenumber mapping in turbulent shear flows.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
166.
Lee, Jin
Ahn, Junsun
and
Sung, Hyung Jin
2015.
Comparison of large- and very-large-scale motions in turbulent pipe and channel flows.
Physics of Fluids,
Vol. 27,
Issue. 2,
Dennis, David J.C.
2015.
Coherent structures in wall-bounded turbulence.
Anais da Academia Brasileira de Ciências,
Vol. 87,
Issue. 2,
p.
1161.
Ahn, Junsun
Lee, Jae Hwa
Lee, Jin
Kang, Ji-hoon
and
Sung, Hyung Jin
2015.
Direct numerical simulation of a 30R long turbulent pipe flow at Re
τ = 3008.
Physics of Fluids,
Vol. 27,
Issue. 6,
Lee, Jin
Kim, Jung Hoon
and
Lee, Jae Hwa
2016.
Scale growth of structures in the turbulent boundary layer with a rod-roughened wall.
Physics of Fluids,
Vol. 28,
Issue. 1,
de Silva, Charitha M.
Hutchins, Nicholas
and
Marusic, Ivan
2016.
Uniform momentum zones in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
309.
Hwang, Jinyul
Lee, Jin
Sung, Hyung Jin
and
Zaki, Tamer A.
2016.
Inner–outer interactions of large-scale structures in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 790,
Issue. ,
p.
128.
Yoon, Min
Hwang, Jinyul
Lee, Jin
Sung, Hyung Jin
and
Kim, John
2016.
Large-scale motions in a turbulent channel flow with the slip boundary condition.
International Journal of Heat and Fluid Flow,
Vol. 61,
Issue. ,
p.
96.
Hwang, Jinyul
Lee, Jin
and
Sung, Hyung Jin
2016.
Influence of large-scale accelerating motions on turbulent pipe and channel flows.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
420.
Pan, Xiaomin
Lee, Changhoon
Kim, Kyoungyoun
and
Choi, Jung-Il
2016.
Analysis of velocity-components decoupled projection method for the incompressible Navier–Stokes equations.
Computers & Mathematics with Applications,
Vol. 71,
Issue. 8,
p.
1722.
Lee, Jae Hwa
2017.
Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
323.
Ahn, Junsun
and
Sung, Hyung Jin
2017.
Relationship between streamwise and azimuthal length scales in a turbulent pipe flow.
Physics of Fluids,
Vol. 29,
Issue. 10,
Lee, Jin
Sung, Hyung Jin
and
Zaki, Tamer A.
2017.
Signature of large-scale motions on turbulent/non-turbulent interface in boundary layers.
Journal of Fluid Mechanics,
Vol. 819,
Issue. ,
p.
165.
Wang, Sung-Ning
Shekar, Ashwin
and
Graham, Michael D.
2017.
Spatiotemporal dynamics of viscoelastic turbulence in transitional channel flow.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 244,
Issue. ,
p.
104.
Kushwaha, Anubhav
Park, Jae Sung
and
Graham, Michael D.
2017.
Temporal and spatial intermittencies within channel flow turbulence near transition.
Physical Review Fluids,
Vol. 2,
Issue. 2,
de Silva, Charitha M.
Kevin, Kevin
Baidya, Rio
Hutchins, Nicholas
and
Marusic, Ivan
2018.
Large coherence of spanwise velocity in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
161.
Wang, Wenkang
Pan, Chong
and
Wang, Jinjun
2018.
Quasi-bivariate variational mode decomposition as a tool of scale analysis in wall-bounded turbulence.
Experiments in Fluids,
Vol. 59,
Issue. 1,
Hu, Ruifeng
and
Zheng, Xiaojing
2018.
Energy contributions by inner and outer motions in turbulent channel flows.
Physical Review Fluids,
Vol. 3,
Issue. 8,
Solak, Ilkay
and
Laval, Jean-Philippe
2018.
Large-scale motions from a direct numerical simulation of a turbulent boundary layer.
Physical Review E,
Vol. 98,
Issue. 3,
Lee, Jin
and
Zaki, Tamer A.
2018.
Detection algorithm for turbulent interfaces and large-scale structures in intermittent flows.
Computers & Fluids,
Vol. 175,
Issue. ,
p.
142.
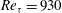 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau }=930$). A streak detection method based on the streamwise velocity fluctuations was used to individually trace the cores of LSMs and VLSMs. We found that both the LSM and VLSM populations were large. Several of the wall-attached LSMs stretched toward the outer regions of the channel. The VLSMs consisted of inclined outer LSMs and near-wall streaks. The number of outer LSMs increased linearly with the streamwise length of the VLSMs. The temporal features of the low-speed streaks in the outer region revealed that growing and merging events dominated the large-scale (1–
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau }=930$). A streak detection method based on the streamwise velocity fluctuations was used to individually trace the cores of LSMs and VLSMs. We found that both the LSM and VLSM populations were large. Several of the wall-attached LSMs stretched toward the outer regions of the channel. The VLSMs consisted of inclined outer LSMs and near-wall streaks. The number of outer LSMs increased linearly with the streamwise length of the VLSMs. The temporal features of the low-speed streaks in the outer region revealed that growing and merging events dominated the large-scale (1–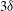 $3\delta $) structures. The VLSMs
$3\delta $) structures. The VLSMs 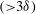 $({>}3\delta )$ were primarily created by merging events, and the statistical analysis of these events supported that the merging of large-scale upstream structures contributed to the formation of VLSMs. Because the local convection velocity is proportional to the streamwise velocity fluctuations, the streamwise-aligned structures of the positive- and negative-
$({>}3\delta )$ were primarily created by merging events, and the statistical analysis of these events supported that the merging of large-scale upstream structures contributed to the formation of VLSMs. Because the local convection velocity is proportional to the streamwise velocity fluctuations, the streamwise-aligned structures of the positive- and negative- $u$ patches suggested a primary mechanism underlying the merging events. The alignment of the positive- and negative-
$u$ patches suggested a primary mechanism underlying the merging events. The alignment of the positive- and negative- $u$ structures may be an essential prerequisite for the formation of VLSMs.
$u$ structures may be an essential prerequisite for the formation of VLSMs.