Article contents
Spatial–spectral characteristics of momentum transport in a turbulent boundary layer
Published online by Cambridge University Press: 12 December 2017
Abstract
Spectral content and spatial organization of momentum transport events are investigated in a turbulent boundary layer at the Reynolds number 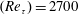 $(Re_{\unicode[STIX]{x1D70F}})=2700$ , with time-resolved planar particle image velocimetry. The spectral content of the Reynolds-shear-stress fluctuations reveals that the largest range of time and length scales can be observed in proximity to the wall, while this range becomes progressively more narrow when the wall distance increases. Farther from the wall, longer time and larger length scales exhibit an increasing spectral content. Wave velocities of transport events are estimated from wavenumber–frequency power spectra at different wall-normal locations. Wave velocities associated with ejection events (Q2) are lower than the local average streamwise velocity, while sweep events (Q4) are characterized by wave velocities larger than the local average velocity. These velocity deficits are almost insensitive to the wall distance, which is also confirmed from time tracking the intense transport events. The vertical advection velocities of the intense ejection and sweep events are on average a small fraction of the friction velocity
$(Re_{\unicode[STIX]{x1D70F}})=2700$ , with time-resolved planar particle image velocimetry. The spectral content of the Reynolds-shear-stress fluctuations reveals that the largest range of time and length scales can be observed in proximity to the wall, while this range becomes progressively more narrow when the wall distance increases. Farther from the wall, longer time and larger length scales exhibit an increasing spectral content. Wave velocities of transport events are estimated from wavenumber–frequency power spectra at different wall-normal locations. Wave velocities associated with ejection events (Q2) are lower than the local average streamwise velocity, while sweep events (Q4) are characterized by wave velocities larger than the local average velocity. These velocity deficits are almost insensitive to the wall distance, which is also confirmed from time tracking the intense transport events. The vertical advection velocities of the intense ejection and sweep events are on average a small fraction of the friction velocity 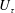 $U_{\unicode[STIX]{x1D70F}}$ , different from previous observations in a channel flow. In the range of wall-normal locations
$U_{\unicode[STIX]{x1D70F}}$ , different from previous observations in a channel flow. In the range of wall-normal locations 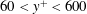 $60<y^{+}<600$ , sweeps are considerably larger than ejections, which could be because the ejections are preferentially located in between the legs of hairpin packets. Finally, it is observed that negative quadrant events of the same type tend to appear in groups over a large spatial streamwise extent.
$60<y^{+}<600$ , sweeps are considerably larger than ejections, which could be because the ejections are preferentially located in between the legs of hairpin packets. Finally, it is observed that negative quadrant events of the same type tend to appear in groups over a large spatial streamwise extent.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
Fiscaletti et al. supplementary movie 1
Time evolution of negative and positive quadrant events of the Reynolds shear stresses. Black dashed lines mark intense Q+ events, while black continuous lines mark intense Q-events. Spots of different sizes and shades mark the time evolution of the weighted centroids of the intense events. The time span covered in this video is 1.33δ/U∞.
Fiscaletti et al. supplementary movie 2
Time evolution of ejection (red) and sweep (blue) events. Black continuous lines mark intense ejection events, while black dashed lines mark intense sweep events. Spots of different sizes and shades mark the time evolution of the weighted centroids of the intense events. The time span covered in this video is 1.33δ/U∞.
- 12
- Cited by


