Article contents
Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number
Published online by Cambridge University Press: 14 December 2018
Abstract
The transport equations for the variances of the velocity components are investigated using data from direct numerical simulations of incompressible channel flows at friction Reynolds number ( $Re_{\unicode[STIX]{x1D70F}}$) up to
$Re_{\unicode[STIX]{x1D70F}}$) up to 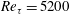 $Re_{\unicode[STIX]{x1D70F}}=5200$. Each term in the transport equation has been spectrally decomposed to expose the contribution of turbulence at different length scales to the processes governing the flow of energy in the wall-normal direction, in scale and among components. The outer-layer turbulence is dominated by very large-scale streamwise elongated modes, which are consistent with the very large-scale motions (VLSM) that have been observed by many others. The presence of these VLSMs drives many of the characteristics of the turbulent energy flows. Away from the wall, production occurs primarily in these large-scale streamwise-elongated modes in the streamwise velocity, but dissipation occurs nearly isotropically in both velocity components and scale. For this to happen, the energy is transferred from the streamwise-elongated modes to modes with a range of orientations through nonlinear interactions, and then transferred to other velocity components. This allows energy to be transferred more-or-less isotropically from these large scales to the small scales at which dissipation occurs. The VLSMs also transfer energy to the wall region, resulting in a modulation of the autonomous near-wall dynamics and the observed Reynolds number dependence of the near-wall velocity variances. The near-wall energy flows are more complex, but are consistent with the well-known autonomous near-wall dynamics that gives rise to streaks and streamwise vortices. Through the overlap region between outer- and inner-layer turbulence, there is a self-similar structure to the energy flows. The VLSM production occurs at spanwise scales that grow with
$Re_{\unicode[STIX]{x1D70F}}=5200$. Each term in the transport equation has been spectrally decomposed to expose the contribution of turbulence at different length scales to the processes governing the flow of energy in the wall-normal direction, in scale and among components. The outer-layer turbulence is dominated by very large-scale streamwise elongated modes, which are consistent with the very large-scale motions (VLSM) that have been observed by many others. The presence of these VLSMs drives many of the characteristics of the turbulent energy flows. Away from the wall, production occurs primarily in these large-scale streamwise-elongated modes in the streamwise velocity, but dissipation occurs nearly isotropically in both velocity components and scale. For this to happen, the energy is transferred from the streamwise-elongated modes to modes with a range of orientations through nonlinear interactions, and then transferred to other velocity components. This allows energy to be transferred more-or-less isotropically from these large scales to the small scales at which dissipation occurs. The VLSMs also transfer energy to the wall region, resulting in a modulation of the autonomous near-wall dynamics and the observed Reynolds number dependence of the near-wall velocity variances. The near-wall energy flows are more complex, but are consistent with the well-known autonomous near-wall dynamics that gives rise to streaks and streamwise vortices. Through the overlap region between outer- and inner-layer turbulence, there is a self-similar structure to the energy flows. The VLSM production occurs at spanwise scales that grow with 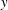 $y$. There is transport of energy away from the wall over a range of scales that grows with
$y$. There is transport of energy away from the wall over a range of scales that grows with 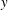 $y$. Moreover, there is transfer of energy to small dissipative scales which grows like
$y$. Moreover, there is transfer of energy to small dissipative scales which grows like 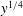 $y^{1/4}$, as expected from Kolmogorov scaling. Finally, the small-scale near-wall processes characterised by wavelengths less than 1000 wall units are largely Reynolds number independent, while the larger-scale outer-layer processes are strongly Reynolds number dependent. The interaction between them appears to be relatively simple.
$y^{1/4}$, as expected from Kolmogorov scaling. Finally, the small-scale near-wall processes characterised by wavelengths less than 1000 wall units are largely Reynolds number independent, while the larger-scale outer-layer processes are strongly Reynolds number dependent. The interaction between them appears to be relatively simple.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: Combustion Research Facility, Sandia National Laboratories, Livermore, CA 94550, USA.
References
- 145
- Cited by

